例析三力平衡与三角形法则

陕西 邢彦君 李丽霞

物体或物体系统，在三个互成角度的外力的共同作用下处于静止状态或匀速直线运动状态，这三个力的合力为零，将表示这三个力的线段保持原方向不变进行平移，使其首尾相接，这三个线段恰好组成三角形。这就是三力平衡的三角形法则，此三角形称为力三角形，其边长表示力的大小，角则表示两个力方向的夹角。对共点力平衡问题中的三力平衡问题，或可划归为三力平衡的多力平衡问题，运用共点力平衡的三角形法则分析求解，将事半功倍。

一、三个恒力的平衡与静态三角形

物体或物体系统在三个恒力的作用下处于平衡状态，做出由表示这三个恒力的矢量构成的三角形，可由解三角形的任何一种方法分析求解力的大小及方向。

【例1】如图1，悬挂甲物体的细线拴牢在一不可伸长的轻质细绳上O点处；绳的一端固定在墙上，另一端通过光滑定滑轮与物体乙相连。甲、乙两物体质量相等。系统平衡时，O点两侧绳与竖直方向的夹角分别为α和β。若α=70°，则β等于

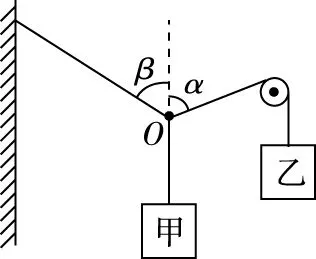
图1

( )

A.45° B.55° C.60° D.70°

【答案】B

【解析】甲、乙物体均处于平衡状态，对其分别运用共点力平衡条件及牛顿第三定律可知，连接它们与O点的两细线对O点的拉力T甲、T乙的大小均等于mg，方向分别沿细线由O点竖直向下、斜向右上。以O点为研究对象，由于O点处于平衡状态，做出由表示O点所受外力的矢量所组成的三角形如图2所示，由题意及几何关系有2β+α=180°，解得β=55°，选项B正确，ACD错误。

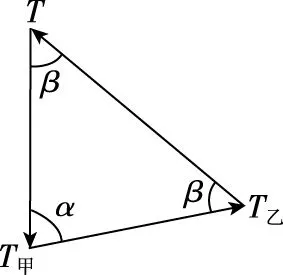
图2

【点评】对三个恒力的平衡问题，运用三角形法则分析求解，便于分析几何关系，且可简化解题过程。

二、有变力的三力平衡与动态三角形

物体或物体系统在三个外力的共同作用下始终处于平衡状态，若其中一个力的方向变化，一个力大小及方向均不变，则另一个力必然变化。对这类三力平衡问题，可灵活选取初始状态，做出初始状态时由表示三个力的矢量组成的三角形，然后在此三角形上重叠做出随变力方向变化后对应的一系列力三角形，由表示力的矢量(三角形的边)长度的变化，可确定变力的大小变化情况。

【例2】如图3所示，水平地面静置一斜面，光滑小物块在水平拉力F的作用下静止在斜面上。现保持小物块静止，将拉力F方向由水平逐渐变成竖直，这一过程中斜面一直静止，则这一过程中

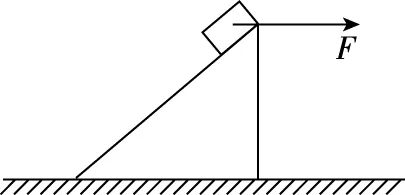
图3

( )

A.F先减小后增大，物块对斜面的压力逐渐减小

B.F先增大后减小，物块对斜面的压力逐渐减小

C.地面对斜面的摩擦力逐渐减小

D.地面对斜面的支持力逐渐减小

【答案】ACD

【解析】小物块始终处于静止状态，由共点力平衡条件可知，表示它所受的重力G、拉力F与斜面的支持力FN的线段将始终构成封闭三角形，如图4所示。由于重力G大小及方向不变，支持力FN方向不变，则随着F方向由水平变成竖直，F先减小后增大，FN逐渐减小。由牛顿第三定律可知，物块对斜面的压力逐渐减小。由图4可知，上述过程中F的竖直分力逐渐增大，水平分力逐渐减小，对物块与斜面整体由共点力平衡条件可知，地面对斜面的摩擦力逐渐减小，支持力逐渐减小，选项B错误，ACD正确。

图4

【点评】对涉及变力的三力平衡问题，运用三角形法则分析求解，不仅可直观显示出变力的变化情况，且很容易看出变力变化过程中的极值。

三、有变力的三力平衡与相似三角形

物体或物体系统在三个外力的作用下始终处于平衡状态，若三力中只有一个力恒定，另外两个力的方向均变化，则做出由表示三个力的矢量组成的三角形，随着力的变化而变化，与此同时，由受力物体(质点)与其他两个空间点构成的空间三角形也随之变化。若力三角形与这个空间三角形相似，可由“相似三角形对应成比例”这一性质列出比例关系，分析求解变力的变化情况。

【例3】如图5所示，将质量为m的小球(可视为质点)，用长为L的轻绳吊起来，并靠在固定在水平面上的半径为r的光滑半球体上的B点。绳的悬点A在半球球心O点的正上方，到球面的最小距离为d。下列结论正确的是

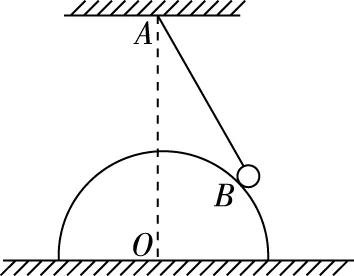
图5

( )

C.若L变长一些，小球对半球体的压力大小不变

D.若L变短一些，轻绳对小球的拉力大小变大

【答案】ACD

图6

【点评】涉及两个力的方向都变化的三力平衡问题，动态三角形的动态顶点不再沿某边移动，可寻找与力三角形相似的空间三角形，灵活运用相似三角形性质列式分析求解。

四、可划归为三力平衡的多力平衡问题

物体或物体系统在多个力的共同作用下始终处于平衡状态，若能先运用力的合成，将多力作用划归为三个力的作用，则可运用共点力平衡三角形法则画出三角形，对变力的变化情况进行分析求解。

【例4】在粗糙水平地面上与墙平行放着一个截面为半圆的柱状物体A，A与竖直墙之间放一光滑圆球B，整个装置处于静止状态。现对B加一竖直向下的力F，F的作用线通过球心，设墙对B的作用力为F1，B对A的作用力为F2，地面对A的作用力为F3。若F缓慢增大而整个装置仍保持静止，截面如图7所示，在此过程中

图7

( )

A.F1保持不变，F3缓慢增大

B.F1缓慢增大，F3保持不变

C.F2缓慢增大，F3缓慢增大

D.F2缓慢增大，F3保持不变

【答案】C

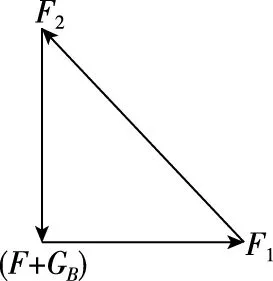
图8

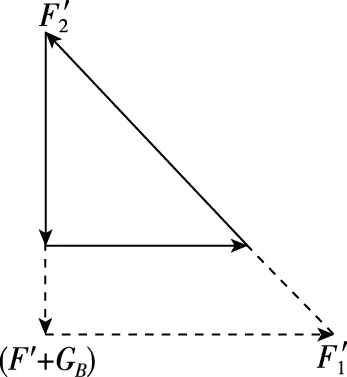
图9

【点评】各力方向均不变的三力平衡问题，运用三角形法则做出的三角形，随某一变力的变大或变小而放大或缩小。

五、三角形法则与圆内接三角形

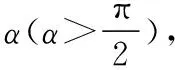
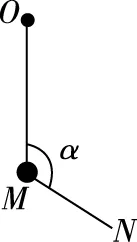
图10

( )

A.MN上的张力逐渐增大

B.MN上的张力先增大后减小

C.OM上的张力逐渐增大

D.OM上的张力先增大后减小

【答案】AD

【解析】选绳OM段稍微倾斜后的某一状态为初始状态，做出此时表示重物所受重力mg、绳OM段的拉力FOM和MN段的拉力FNM三个力的矢量组成的三角形，如11图所示。由于将重物向右上方缓慢拉起，并保持夹角α不变，则三角形中表示重力mg的矢量所对应的角不变，随着重物被斜向右上缓慢拉起，三角形中表示重物两侧绳拉力的矢量的交点，将沿三角形的外接圆向上移动。由表示力的矢量的长度的变化可知，MN上的张力逐渐增大，OM上的张力先增大后减小，AD正确，BC错误。

图11

【点评】在圆中，同弧或等弧对应的圆周角相等；找出三角形的外心，便可画出三角形的外接圆。

受力分析、状态分析，是物理学的基本分析方法，与此对应的共点力平衡条件及应用问题，是高考的必考点，三力平衡则是高考考查共点力平衡现象或问题的高频模型。分析求解三力平衡问题的基本思路与方法，一是灵活选取研究对象，将其视为质点。这里的研究对象，可以是处于平衡状态的某个物体或物体系统，也可能是绳结或杆的端点；二是正确分析研究对象的受力情况，画出受力示意图，这里要特别注意静摩擦力的有无及其方向的判断，注意弹簧或杆的弹力方向的判断；三是依据各力的方向，画出由表示三个力的矢量构成的三角形，并由问题情境确定力三角形中已知的角和边，或确定实际问题中变化因素的变化引起的力三角形中相应的变化量(某个角度的大小)的变化情况；四是求出与所求的力的大小(或方向)对应的三角形的边长(或角度)，或判断出与三角形的边对应的力的大小的变化情况，这里要特别注意的是的最值或极值的判断。