公铁平层斜拉桥列车-桥梁耦合振动分析
2021-11-08何佳骏向活跃韩冰李永乐
何佳骏 向活跃 韩冰 李永乐
1.西南交通大学土木工程学院,成都610031;2.四川省铁路产业投资集团有限责任公司,成都610094
随着桥位资源的不断紧缺,公铁两用缆索承重桥梁逐渐得到广泛的应用。因其兼具列车线路与公路车道,比单一线路种类的桥梁拥有更高的运载能力。公铁平层箱梁桥作为公铁两用桥梁的一种形式,能够承受较大的轴向荷载,在缆索承重桥梁中具有独特的优势[1]。但其桥面宽度较大,列车荷载与汽车荷载往往距离桥梁中心线较远,汽车荷载的偏载作用可能会引起更大的响应。汽车与列车同时行驶会进一步增加车辆动力响应的复杂性[2]。
国内外学者对各种类型的桥梁与车辆的耦合振动进行了大量研究,包括连续梁桥[3]、简支梁桥[4]、曲线梁桥[5]、大跨度斜拉桥[6-7]、拱桥[8]等,全面分析了车桥系统的动力响应。对多线铁路桥梁的车桥响应进行分析时发现,列车的线路越靠近桥梁中心线,桥梁的动力响应越大,车辆的动力响应越小[9-12]。由于大跨度桥梁刚度较小,多线铁路的车桥耦合振动响应往往比单车线铁路时大。
对于公铁两用桥梁的车桥耦合响应,安会峰[13]通过建立汽车-桥梁-列车耦合系统,研究了汽车与列车同时通过桥梁时三者动力响应相互影响的规律。刘高等[14]通过车-桥耦合动力系统研究了跨海公铁两用斜拉桥的耦合振动响应。钟豪[15]以马岭河公铁两用钢桁梁悬索桥为背景,研究了有轨电车和汽车通过桥梁时的车桥系统响应。总体而言,汽车对列车-桥梁动力响应有一定影响,汽车对低速的城市轨道交通影响不大,但对高速列车有较明显的影响,且随列车速度的增加而增加。公铁平层桥梁主梁整体竖向刚度更小,桥面更宽,汽车偏载对行车性能影响更大。上述文献关于公铁两用桥梁行车性能的研究多针对双层桁架结构,而对公铁平层桥梁的研究较少。
本文以宜宾临港长江大桥为背景,采用车-桥耦合振动的分析方法计算列车通过桥梁时的车桥系统响应,研究列车速度及线路类型对响应的影响;分析不同线路组合下,双车行驶过桥时列车之间的相互影响,以及公路车道荷载对列车走行性的影响。
1 工程背景
宜宾临港长江大桥为双塔连续钢箱梁斜拉桥,跨径布置为(72.5 + 203 + 522 + 203 + 72.5)m,主桥全长1 075.5 m。主梁采用整体式钢箱梁,梁高5 m,横桥向设双向2%横坡。桥面采用公铁平层布置的形式,四线高速铁路设置在桥面中间,对称布置,两侧各布置三车道城市道路、人行道和非机动车道。四线铁路线间距为(6.5+5+6.5)m,外侧铁路线路中心线到铁路防撞墙外侧的距离为4.1 m。公铁间的索梁锚固区域宽度为1.8 m。铁路桥面宽26.2 m,城市道路宽12.75 m,非机动车道+人行道+护栏的总宽为2.5+1.5 + 0.3 = 4.3 m,桥面总宽63.9 m。铁路设计速度300 km/h,公路设计速度80 km/h。主梁截面如图1 所示。为方便对车桥耦合计算工况进行描述,对铁路及公路进行编号并对线路类型进行定义。列车单车过桥线路类型:内侧线路为2 线和3 线;外侧线路为1 线和4线。列车双车交会线路类型:对称布置线路组合,1 线 +4 线 ,2 线 +3 线 ;偏 载 线 路 组 合 ,1 线 +2 线 ,1 线+3 线,2 线+4 线,3 线+4 线;完全偏载线路组合,1线+2线,3线+4线。

图1 主梁截面(单位:mm)
2 车-桥耦合振动模型
车-桥耦合振动模型中,车辆模型由1 个车体,2个转向架及4 个轮对共7 个刚体构成,车体与转向架之间通过弹簧阻尼连接,转向架与轮对通过二系轴箱相连,在考虑轮对横向和摇头自由度的条件下,列车模型共计23 个自由度[16-17]。文中选取的列车为CRH3型列车,列车编组为16节。
根据D’Alembert 原理,可建立车辆模型的运动方程,即
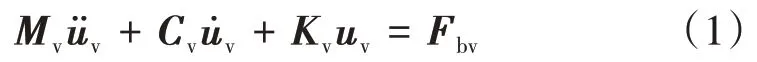
式中:Mv、Cv、Kv分别为车辆子系统的集中质量矩阵,阻尼系数矩阵和刚度矩阵分别为车辆子系统的位移矩阵、速度矩阵和加速度矩阵;Fbv为车辆子系统受到的车桥相互作用力矩阵。
建立桥梁有限元模型(图2)。虽然主梁宽度较宽,但其跨度较大,斜拉索锚固于公路和铁路之间,且主梁采用了正交异性板,每隔4.0 m 设有横隔板,横向刚度大,认为平截面假定是成立的。因此,主梁、桥塔及桥墩均采用空间梁单元模拟,斜拉索采用杆单元模拟;二期恒载采用Mass21质量单元。

图2 1/2桥梁有限元模型
桥梁结构的运动方程为

式中:Mb、Cb、Kb分别为桥梁子系统的集中质量矩阵,阻尼系数矩阵和刚度矩阵分别为桥梁子系统的位移矩阵、速度矩阵和加速度矩阵;Fvb为桥梁子系统受到的车桥相互作用力矩阵。
采用自主研发的桥梁结构分析软件BANSYS,利用分离迭代法求解车辆与桥梁子系统的响应,轨道不平顺采用德国低干扰谱进行模拟,计算的空间步长取0.2 m。为研究线路类型对车辆响应的影响,铁路各线路均采用相同的轨道不平顺。
3 车桥响应计算结果分析
3.1 线路位置的影响
列车以300 km/h 车速从线路1 和线路2 通过桥梁时,选取拖车的响应进行计算分析。车辆和桥梁的响应分别见表1和表2。其中,跨中扭转角为沿桥轴线方向的扭转角。
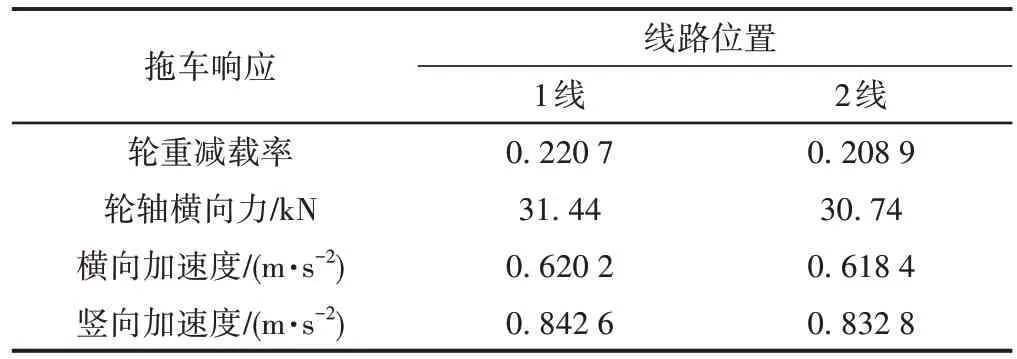
表1 内外侧线路单车行驶过桥的拖车响应
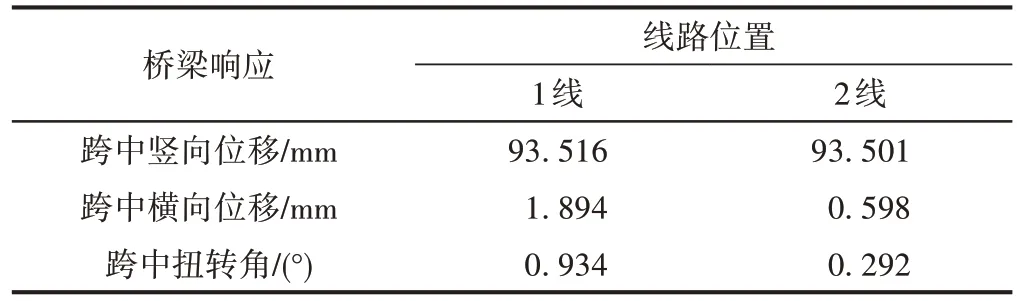
表2 内外侧线路单车行驶过桥的桥梁响应
由表1 和表2 可知:不同线路位置车辆响应差距较小,桥梁的扭转角和横向位移差距较大,但桥梁位移总体较小。大跨度桥梁位移的波长较长,因此对行车安全性影响有限。列车在内外侧线路行驶对跨中竖向位移影响较小,列车线路偏心距离的增大主要引起桥梁的横向位移和扭转角的增大。
3.2 车速的影响
当列车位于线路1 时,分析列车以200 ~350 km/h车速通过桥梁时车辆和桥梁的响应,计算结果分别见表3和表4。

表4 列车通过桥梁时的桥梁响应
由表3 可知,车辆的各项响应均随车速的增加而增加。各车速下动车的脱轨系数、轮重减载率和轮轴横向力均小于拖车,而横竖向加速度与拖车接近,原因是动车轴重比拖车大。因此,以拖车为研究对象对各项影响指标进行分析。

表3 列车通过桥梁时的车辆响应
由表4 可知,虽然不同车速下桥梁响应有一定的离散性,但总体上桥梁的响应随车速的增加而增加,当车速为350 km/h 时,竖向挠跨比为1/5 394。若将6 车道公路近似为单线的铁路荷载计算,在公路与铁路荷载同时施加的条件下桥梁主跨的挠跨比约为1/1 076,说明桥梁有较大的竖向刚度。
3.3 双车交会的影响
车速为300 km/h 时,列车以不同入桥距离差、不同线路位置对向通过桥梁时,先行侧(先出发的车辆)和后行侧(后出发的车辆)的车辆中拖车的脱轨系数分别见表5 和表6。其中,0 表示两车同时入桥,L/8 表示先行侧车辆行驶1/8 的桥长后,后行侧车辆开始入桥,L为桥梁总长。

表5 先行侧车辆最大脱轨系数
由表5 和表6 可见:①后行侧拖车的脱轨系数受线路组合影响比先行侧拖车更明显。先行侧拖车各线路之间的脱轨系数接近,而后行侧不同线路组合的脱轨系数差距较大。②非对称线路(1 线+2 线和1 线+3 线)车辆的脱轨系数大于对称布置的线路(1 线+4 线和2 线+3 线),这是由于车辆在非对称线路行驶时桥梁横向响应更大。偏载最大的线路(1线、2线)的内线列车脱轨系数最大。③随着入桥距离差的增加,受另外一辆列车的影响逐渐减弱,偏载线路先行侧列车和后行侧列车的脱轨系数差距逐渐减小。④双车过桥的偏载工况中,另一辆列车的存在增加了内线列车的脱轨系数,而几乎不影响外线列车的脱轨系数。

表6 后行侧车辆最大脱轨系数
双车在不同线路组合、入桥距离差下通过桥梁时,先后行侧拖车最大轮重减载率分别见表7和表8。

表7 先行侧车辆最大轮重减载率
由表7 和表8 可知:①先行侧车辆的轮重减载率总体大于后行侧车辆。线路组合对先行侧和后行侧拖车轮重减载率的影响相反。对于先行侧拖车,偏载线路具有更大的轮轴减载率,而后行侧拖车在对称线路上具有更大的轮重减载率。②对称线路中,外线对称布置车辆的轮重减载率大于内线对称布置车辆。③随着入桥距离差的增大,先行侧拖车各线路之间轮重减载率差距逐渐减小,而后行侧拖车的差距逐渐增大,这可能是先行侧车辆通过时引起桥梁振动造成的。④列车在偏载线路行驶时,先行侧拖车的轮重减载率增大,后行侧拖车根据车距的增加则有一定幅度的减小或增大。原因是先行侧车辆上桥后产生的桥梁振动对车辆形成了一种反馈,即桥梁的振动与轨道不平顺叠加形成的外激力改变了后行侧车辆的轮重减载率,这一现象在非对称线路中更加明显。
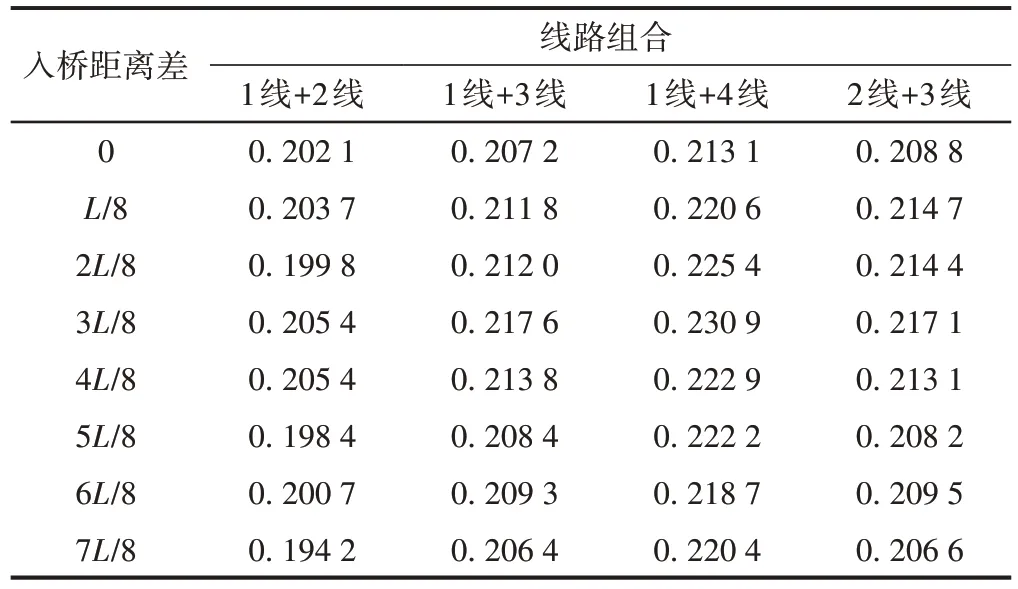
表8 后行侧车辆最大轮重减载率
双车在不同线路组合、不同入桥距离差下通过桥梁时,先后行侧拖车轮轴横向力分别见表9和表10。
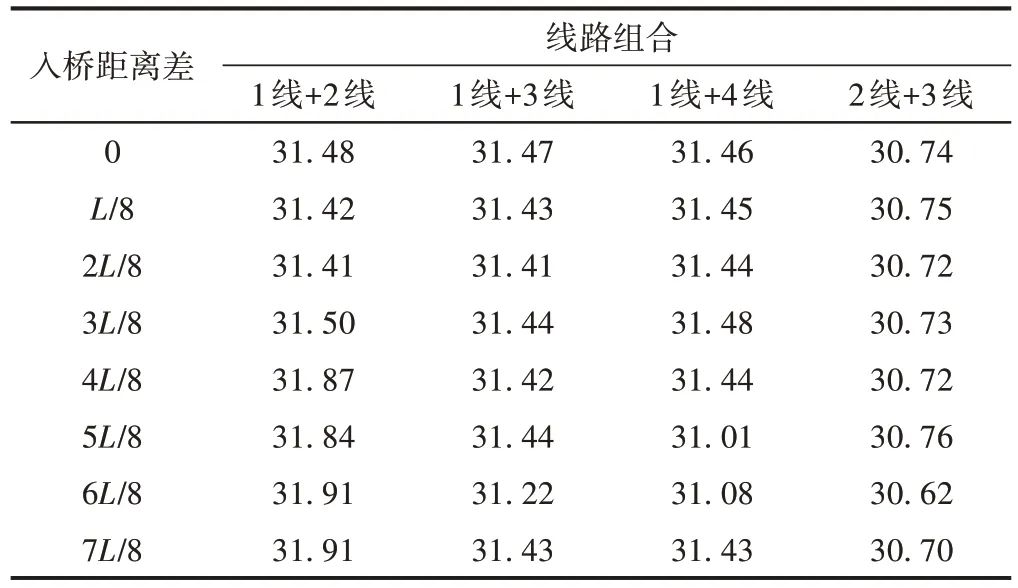
表9 先行侧车辆轮轴横向力 kN

表10 后行侧车辆轮轴横向力 kN
由表9 和表10 可知:①轮轴横向力与脱轨系数有相同的变化规律,即后行侧拖车的轮轴横向力受线路组合影响比先行侧拖车更明显。先行侧拖车各线路之间的轮轴横向力接近,而后行侧不同线路组合的拖车差距较大。②非对称线路车辆的脱轨系数明显大于对称布置的线路。完全偏载线路组合的内线列车轮轴横向力最大。③随着入桥距离差的增加,偏载线路先行侧和后行侧列车的脱轨系数差距整体上逐渐减小。④与单车过桥相比,非对称线路组合的后行侧车辆具有更大的轮轴横向力,且在入桥距离差为2L/8~3L/8 时达到最大。
综上,双车过桥时偏载线路会引起更大的横向位移,导致车辆横向振动剧烈,使得车辆的横向响应相关指标(脱轨系数、轮轴横向力)上升。对于竖向响应相关指标(轮重减载率)而言,先行侧车辆通过时引起的振动与轨道不平顺叠加,能够减弱或加强后行侧车辆的竖向振动,从而改变轮重减载率。完全偏载线路为列车安全指标的最不利线路。
双车在不同线路组合、不同入桥距离差下通过桥梁时桥梁跨中的最大响应见表11—表13。可知:①不同的线路组合对桥梁的最大竖向位移影响较小,对横向位移及扭转角影响较大。②完全偏载线路具有最大的横向位移及扭转角。由于列车在非同侧线路(1 线+3 线,1 线+4 线,2 线+3 线)行驶时,对桥梁产生的竖向激励作用的力矩相反,桥梁的横向位移及扭转角比单车过桥时小。③当入桥距离差超过4L/8 时,两列车辆对桥梁响应的叠加作用逐渐消失。

表11 桥梁最大竖向位移 mm

表12 桥梁最大横向位移 mm
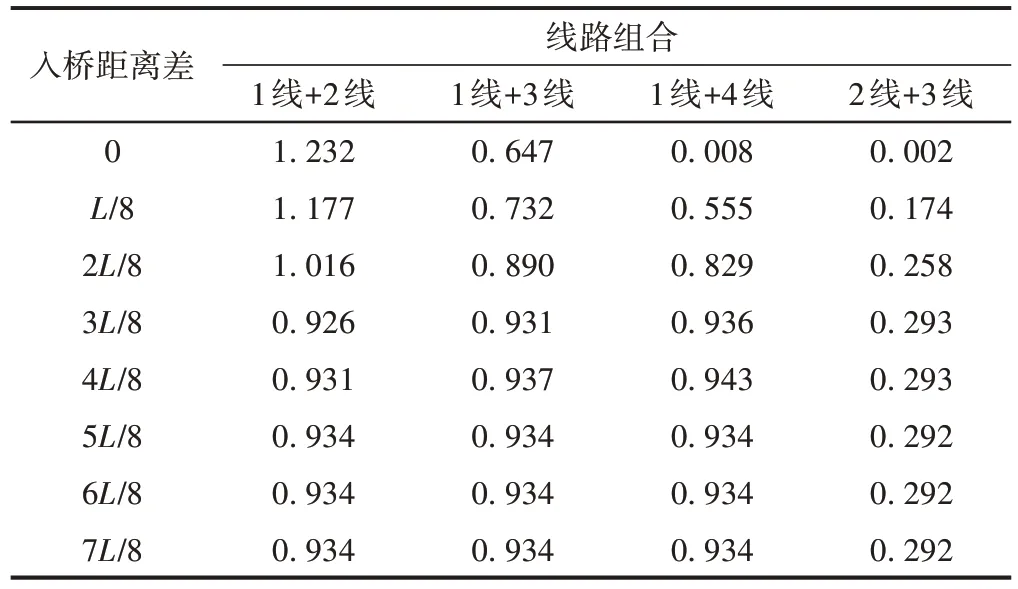
表13 桥梁最大扭转角 (°)
3.4 公路车道荷载的影响
根据JTG D60—2015《公路桥涵设计通用规范》4.3.1 条,采用均布荷载和集中荷载模拟车道荷载进行计算。公路-I级车道均布荷载标准值为10.5 kN/m,集中荷载取360 kN。均布荷载应满布于使结构产生最不利效应的影响线上;集中荷载只作用于相应影响线中一个影响线峰值处。根据JTG D60—2015,横向布载系数取0.78,纵向布载系数取0.96。将车道荷载布置于车道4—车道6,对公路车道荷载作用下的车桥耦合响应进行计算。列车以300 km/h 车速通过桥梁时,各条线路上拖车的最大脱轨系数、最大轮重减载率和最大加速度分别见表14—表16。

表14 拖车最大脱轨系数和最大轮重减载率
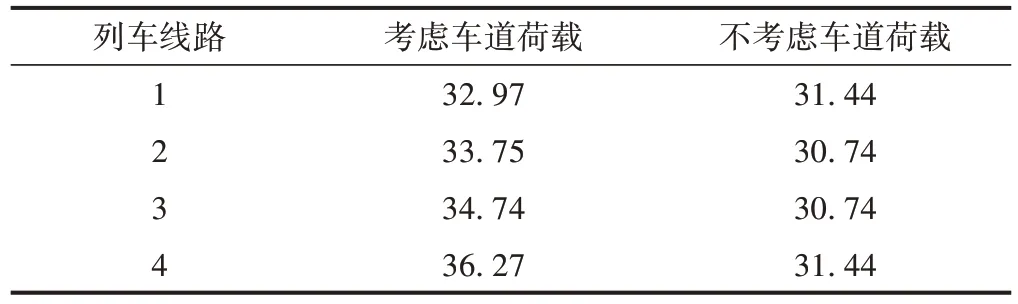
表15 拖车最大轮轴横向力 kN

表16 拖车最大加速度 m·s-2
由表14—表16可知:车道荷载会引起内外侧线路车辆响应增加,且距离公路车道越近的线路,列车的最大脱轨系数与最大轮重减载率越大;车道荷载使各线路列车脱轨系数、轮重减载率及轮轴横向力提高了10%左右。针对响应最大的线路4,与不考虑车道荷载相比,考虑车道荷载时脱轨系数、轮重减载率、轮轴横向力分别提高了11.36%、6.21%、15.36%。车道荷载对于列车的横向加速度及竖向加速度也有明显提升,但不同线路列车之间的差距并不明显。
将车道荷载布置于车道4—车道6,列车以车速300 km/h 通过桥梁时,桥梁最大位移和最大扭转角分别见表17和表18。可知:车道荷载显著增大了桥梁主跨跨中的各项响应;不同线路之间的竖向位移差距并不明显。原因是与列车荷载相比,车道荷载占竖向激励的主导,所以各个线路产生的竖向激励比较接近,桥梁竖向振动差距不大。列车线路越靠近公路车道,线路偏载越明显,横向位移及扭转角越大。
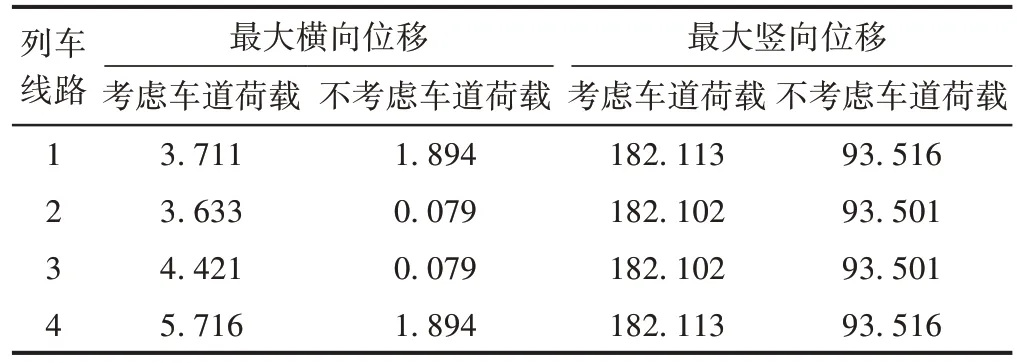
表17 桥梁最大位移 mm

表18 桥梁最大扭转角 (°)
4 结论
1)单车行驶通过桥梁时,外侧线路行驶的车辆的响应稍大于内侧车辆。列车在外侧线路行驶时桥梁横向位移及扭转角明显大于内侧线路,但竖向位移差距不大。
2)双车对向行驶通过桥梁时,偏载线路会导致车辆的脱轨系数、轮轴横向力增加,且内侧线路行驶的相关指标更大。根据两列列车的入桥距离差,先行侧车辆对后行侧车辆的轮重减载率会产生不同的影响;各线路组合下桥梁的竖向位移差距并不明显,但偏载线路会引起桥梁更大的横向位移及扭转角。
3)公路车道荷载作用下,列车通过桥梁时各项响应均增加。越靠近公路车道的列车线路,列车的脱轨系数与轮重减载率越大。列车在不同线路行驶时,桥梁的竖向位移差距并不明显,靠近公路车道的列车线路会使桥梁产生更大的横向位移及扭转角。
