小学高年级学生数学学习策略量表的设计与编制

2021-11-08王光明

心理研究 2021年5期

王瑶李健王光明

（1 郑州市郑东新区文苑学校，郑州 450018；2 人民教育出版社课程教材研究所，北京 100081；3 天津师范大学教育学部，天津 300387）

近年来，如何合理有效地减轻中小学生的学业负担问题，已成为我国基础教育改革的关注重点。2018 年12 月，教育部等九部门发布《关于印发中小学减负措施的通知》，指出要切实减轻中小学生的过重学业负担。在减少学生学业负担的各种应对措施中，提升学习效率是一种行之有效的方式。由于学生的学习效率与其学习策略紧密联系，因此研究学生的学习策略也就尤为必要。

教育心理学研究显示，学习策略在自我调节学习中具有重要意义（周国韬，张林，2002），学习策略能够影响学生的学业成绩（Fadlelmula，Cakiroglu，＆Sungur，2015；毛秀珍，王娅婷，韦嘉，2017；陈鹃娟，周莹，2020）。学生掌握和运用学习策略的能力与经验的增长密切相关（周国韬，张平，李丽萍，刘晓明，1997），即不同年龄阶段的学生具有不同的学习策略特征。只有采用科学有效的测量工具，才能更好地了解小学生的数学学习策略。目前，已有较多学者对数学学习策略的测评工具展开研究。

对于学习策略的界定，学界意见不一。有学者将其定义为一种内隐的调节规则（Duffy，1982），也有学者将其定义为内隐性与外显性结合的统一体（张庆林，1995）。二十世纪九十年代以后，我国学者更多地倾向于后者，认为学习策略不仅包含学习者的认知方法，还包括学习者的调控行为。宏观地看，学习策略可分为通用学习策略与学科学习策略，数学学习策略便属于学科学习策略的范畴。数学学习策略是具有数学学科属性的学习策略，数学学习策略测评工具的研制需借鉴学习策略测评工具的编制经验。

概念界定的不一致，使得学习策略的结构划分不尽相同。例如Weinstein 认为学习策略可分为认知信息加工策略、积极学习策略、辅助性策略和元认知策略（刘儒德，1997）；Mckeachie 将学习策略划分为认知策略、元认知策略、资源管理策略（陈琦，刘儒德，1997）；OECD（2013）将学习策略分为记忆复述策略、精细加工策略、元认知监控策略。在对学习策略的概念、内涵的不断深入研究过程中，相应的一些学习策略测评问卷也得到开发，例如学习与策略量表（learning and strategies inventory）（Weinstein ＆Mayer，1986），学习动机策略问卷（motivated strategies for learning questionnaire）（Schunk， Pintrich，＆ Meece，1995）等。

随着研究者们对学习策略研究的深入，关于数学学习策略调查问卷的研究也逐步发展起来。但国内外对数学学习策略研究的侧重点却有所不同，国外研究者更加侧重于一些具体数学学习策略的研究，而国内研究者则更倾向于涉及内容更宽泛的数学学习策略。随着近年来我国对教育测评的关注，数学学习策略问卷的编制也逐步发展起来。

刘电芝（2003）编制了小学生数学学习策略量表，将数学学习策略分为数学元认知策略与数学认知策略。莫秀锋与刘电芝（2005）共同进行了初中生数学学习策略的可控心理影响机制研究，其中使用自编的初中生数学学习策略量表将数学学习策略分为三个维度：认知策略、元认知策略、资源管理策略，这种划分方式与Mckeachie 的划分方式一致（陈琦，刘儒德，1997）。至此之后，我国研究者对于数学学习策略量表的主维度划分基本达成一致。刘苏蛟、赵守盈与郭金龙（2010）编制的高中生数学学习策略量表，吴现荣与宋军（2017）编制的适用于少数民族地区的初中生数学学习策略量表，曹一鸣与陈鹏举（2018）编制的中学生数学学习策略调查问卷，以及王光明团队编制的高中生数学学习策略调查问卷（王光明，廖晶，黄倩，王兆云，McDougall，2015）和初中生数学学习策略调查问卷（王光明，刘丹，2017），均将数学学习策略分为三个维度：数学认知策略、数学元认知策略、数学资源管理策略。但需要指出的是，尽管我国研究者对数学学习策略主维度的确立逐步趋同，但对于各主维度的下属子维度的选择仍有差异。以数学资源管理策略为例，曹一鸣与陈鹏举（2018）认为数学资源管理策略包括时间安排、自主参考、寻求支持，而王光明与刘丹（2017）则将数学资源管理策略界定为时间管理策略、环境管理策略、心境管理策略和外界求助策略。

综上所述，目前我国研究者对数学学习策略的主维度划分呈现出一种趋同认识，包括数学认知策略、数学元认知策略、数学资源管理策略，相关量表也基本是基于这种三维度划分而编制的。但许多量表在子维度的确立上仍有差异，有待进一步的研究。而从量表的适用对象来看，大量数学学习策略量表都是针对中学生和大学生的，可供小学生使用的量表相对较少。又考虑到小学阶段学生的年龄跨度大，使用同一量表测评所有年级学生并不合适。而小学高年级学生的学习策略得到较大发展且相对稳定（梁宇，2010；慕德芳，陈英和，2021），故确定研究问题为：小学高年级学生数学学习策略量表是什么？研究将按照科学的量表编制程序，开发针对我国小学高年级（5～6 年级）学生的数学学习策略量表，为其数学学习策略的测量提供有效工具。

1 问卷编制过程与方法

1.1 问卷维度及其操作性定义的确定

基于王光明与刘丹（2017）对初中生数学学习策略的维度划分，所编问卷将数学学习策略划分为数学认知策略（在数学学习过程中对学习信息的记忆、重组、检索及精加工）、数学元认知策略（在数学学习过程中对学习计划的制定、修改，对学习活动的监控、调节，对学习结果与经验的反思）、数学资源管理策略（对课下数学学习时间、数学学习环境、数学学习心境和寻求他人帮助等方面的管理）。与此同时，基于已有研究（莫秀峰，2002；刘电芝，2003；王光明，刘丹，2017）对数学学习策略的子维度划分，进一步又可以划分出十个子维度。综上，本研究认为数学学习策略包含三个主维度以及十个子维度，并结合已有研究关于十个子维度的定义，给出各子维度的操作性定义，见表1。

表1 小学高年级学生数学学习策略量表子维度的操作性定义

1.2 量表题目的建立

综合考虑小学高年级学生数学学习的特点，基于对已有量表或问卷存在的问题以及注意事项的研究，建立量表题目库。量表题目库的题目主要来自于：Weinstein 与 Mayer （1986）的学习与策略量表，Pintrich 的学习动机和学习策略量表（朱莎，2016），PISA2012 学生学习策略问卷（OECD，2013），王光明与刘丹（2017）的初中生数学学习策略调查问卷，刘电芝（2003）的小学数学学习策略量表。从题目库中挑选合适题目，并进行必要修改，形成包含86 道题目（80 道正式题目与6 道测谎题）的第一版问卷，其中考察数学认知策略的题目有25 道，考察数学元认知策略的题目有26 道，考察数学资源管理策略的题目有29 道。

1.3 被试选取与问卷回收

问卷编制过程中，共进行了4 次问卷发放与回收，若回收问卷出现多选、遗漏或作答不认真等情况，则视为无效问卷。第一步目测辨别，将作答结果呈现规律性或同一性特点的试卷视为无效问卷。第二步依据测谎题检测，当问卷所有信息录入后，将测谎题作答差异性较大的问卷视为无效问卷。四次样本的信息如表2 所示。

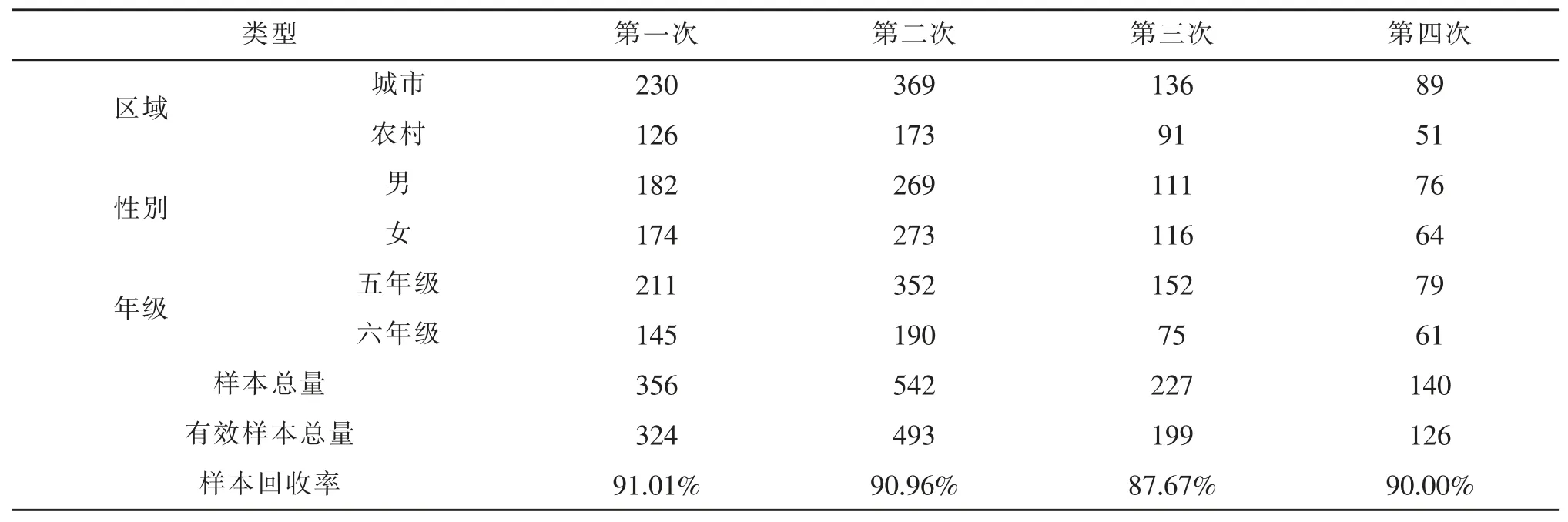
表2 量表编制阶段样本信息

样本一为预测试样本，利用此样本进行项目分析和探索性因素分析。选取天津市鞍山道小学、咸阳路小学、八里台第四小学的5～6 年级学生作为问卷发放对象。共收集问卷356 份，有效问卷324 份，有效率为 91.01%。

样本二为大规模施测样本，主要用于进行探索性因素分析。选取天津市鞍山道小学、天津市滨海新区新港第二小学、河南省开封市仁和小学、陕西省西安市曲江南湖小学、江苏省盐城阜宁实验小学的5～6 年级学生作为问卷发放对象。共收集问卷542 份，有效问卷493 份，有效率为90.96%。

样本三为问卷修订过程中验证性因素分析所用样本。选取天津市八里台第四小学、塘沽区桂林路小学，以及河南省开封市大厅门小学的5～6 年级学生作为问卷发放对象。共收集问卷227 份，有效问卷199 份，有效率为 87.67%。

样本四为重测样本。选取的是样本二中的鞍山道小学、仁和小学的5～6 年级学生作为问卷发放对象。共收集问卷140 份，有效问卷126 份，有效率为90.00%。

1.4 数据分析工具

利用SPSS18.0 进行项目分析、探索性因素分析以及各类信度检验等，利用AMOS21.0 进行验证性因素分析。

2 问卷的预研究结果与分析

2.1 项目分析

采用SPSS18.0 对预测试数据进行项目分析。第一步，采用同质性检验筛选题目。计算各题目得分与问卷总分之间的Pearson 相关系数，删除相关系数小于 0.4 的题目（吴明隆，2010），共 18 道。第二步，利用决断值进行极端组检验，对高分组（总得分前27%）与低分组（总得分后27%）的被试数据进行独立样本t 检验，删除未达到差异显著性要求（p<0.05）的题目，共 8 道。经过项目分析，问卷剩余题目54 道。

2.2 探索性因素分析

对数学学习策略总体以及三个主维度分别进行KMO 检验和Bartlett 球形检验。总问卷及三个主维度的 KMO 值处于 0.87～0.93 之间，均大于 0.85，达到可接受水平；且Bartlett 球形检验值达到显著水平（p<0.01），各变量间具有较好相关性。故总问卷及各主维度均适合进行探索性因素分析。

研究采用主成分分析法与最大方差旋转法，以此确定问卷维度与相应题目。根据探索性因素分析的删题原则（王光明，刘丹，2017），进行探索性因素分析并删减题目后，剩余44 道。尽管数据指标可以作为筛选题目的依据，但不能仅仅依靠数据进行删题。通过对问卷发放对象的访谈发现：第一，由于题量较大，且学生年龄较低，导致部分学生作答时无法持续集中注意力；第二，学生未能完全理解所有题目的表达方式和内容，使得回收答案与真实情况具有一定偏差。因此，删题时并非仅依靠统计分析结果，还兼顾问卷题目的内容和维度进行多方面考虑。经过上述操作对小学高年级学生数学学习策略量表（第一版）的部分题目进行修改，并增补个别题目，形成小学高年级学生数学学习策略量表（第二版），共48 道题目（44 道正式题目和4 道测谎题）。

3 问卷的正式确定及结果分析

3.1 项目分析与探索性因素分析

使用第二版问卷进行大规模施测，与预测试研究中的方式相似，首先采用同质性检验筛选题目，之后利用决断值进行极端组检验，共剔除10 道题，剩余34 道（测谎题除外）。而后对数据进行探索性因素分析，结果（见表3）表明问卷因子确定合理，与理论框架较为吻合，进而形成第三版问卷。

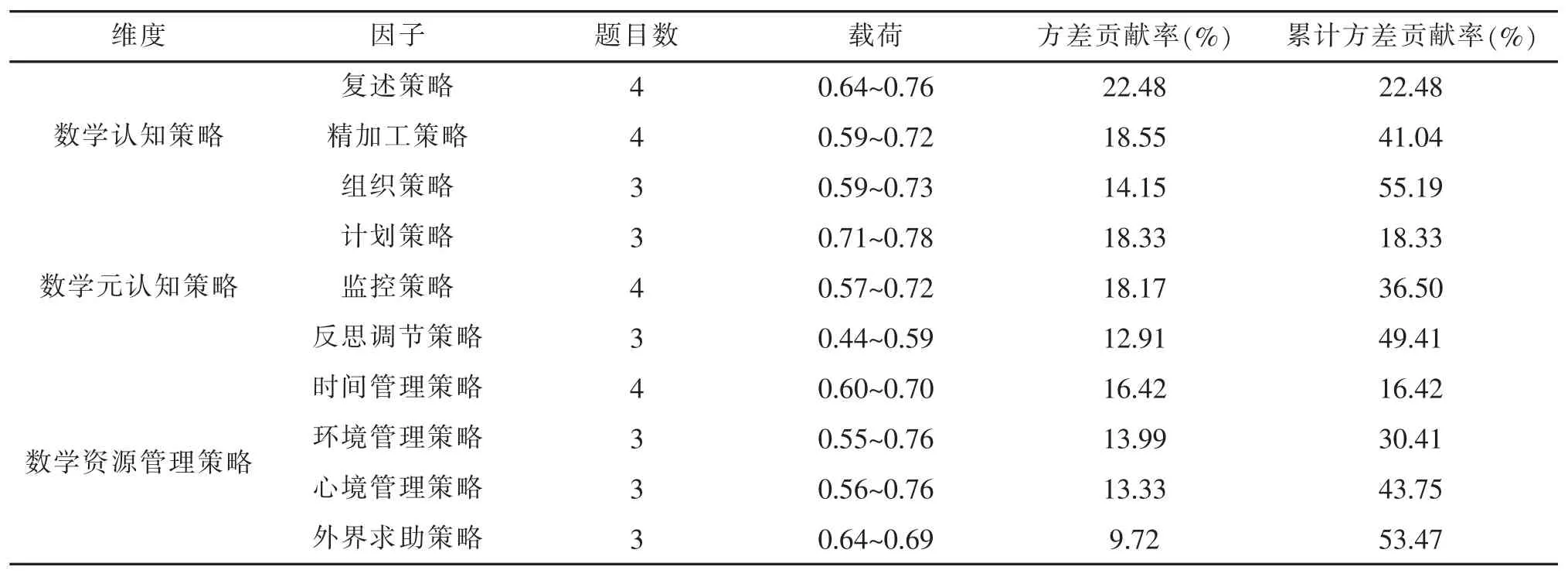
表3 小学高年级学生数学学习策略探索性因素分析结果

3.2 验证性因素分析

使用第三版问卷施测，对收集到的样本三进行验证性因素分析。首先利用数据对初始的一阶10 因子模型进行拟合，通过对初始模型的一阶因子进行检验，基于对各题目的因子载荷值以及修正指数MI值的考察发现：有两道题的因子载荷值小于0.5，将其删除；并且有两对题目的MI 值大于20（第6 题和第30 题，第17 题和第22 题），表明每对题目中的两道题存在较强相关性，分析具体内容后删除其中的两道题目（第17 题和第30 题），此时问卷剩余30 道题。

再进行一阶10 因子二阶3 因子模型的验证性因素分析，选取 χ2／df，RMSEA，NFI，TLI，CFI，GFI 作为模型拟合程度的评价指标，各项拟合指数见表4，因子的标准化载荷值及结构间的路径系数见图1。在二阶模型中，各拟合指数都达到基本要求，且与一阶10 因子模型相比，拟合指数更好。

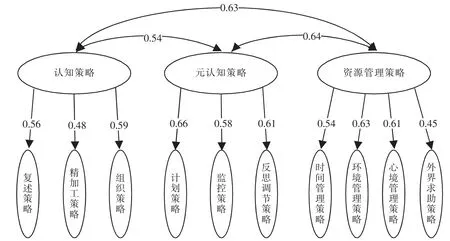
图1 小学高年级学生数学学习策略结构的路径系数

表4 一阶10 因子二阶3 因子模型拟合指数

3.3 问卷的信度和效度检验

3.3.1 信度分析

信度是衡量问卷稳定性的指标，正式的问卷调查中，共有30 道关于数学学习策略的题目。为探究正式问卷的稳定性，对样本二中的鞍山道小学、仁和小学的学生进行再测，分为两个步骤进行操作：第一步，采用 Cronbach’s 系数、Spearman－Brown 的分半信度衡量问卷的稳定性；第二步，采用相关分析计算两次测试相同题目的Pearson 相关系数（见表5）。结果表明，小学高年级学生数学学习策略量表具有较高的内部一致性，且选取的小学高年级学生在不同时间得分一致性也较高，即量表具有较高的外部一致性。

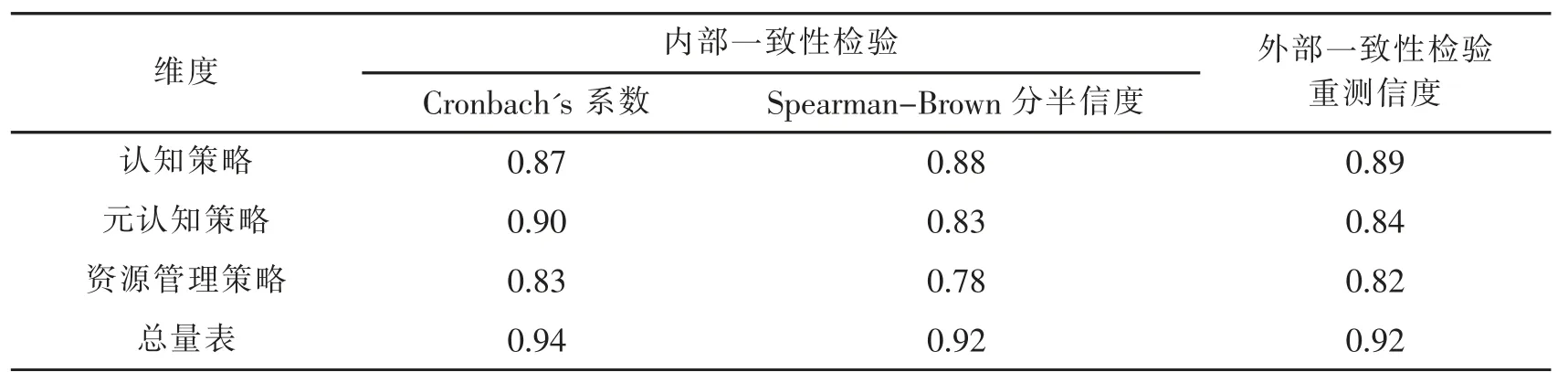
表5 小学高年级学生数学学习策略量表的信度检验指标

3.3.2 效度分析

3.3.2.1 结构效度

将验证性因素分析的结果作为结构效度是否合格的评价指标。施测数据对一阶10 因子二阶3 因子模型的拟合指数为：χ2／df＝3.92，RMSEA＝0.08，NFI＝0.97，TLI＝0.95，CFI＝0.98 和 GFI＝0.97，表明所测数据可以较好地拟合所设模型，问卷具有较好的结构效度。

此外，研究还计算了各主维度得分与总问卷得分之间的相关系数，发现三个维度间的相关系数介于 0.76～0.83 之间，表明数学认知策略、数学元认知策略以及数学资源管理策略两两之间呈现中度相关，而三个主维度与问卷整体水平的相关系数介于0.91～0.95 之间，均大于 0.9，表明各维度与总量表得分之间存在高度相关。

3.3.2.2 效标关联效度

选用PISA2012 学生学习策略问卷作为效标检验的参照工具，计算小学高年级学生数学学习策略量表的效标关联效度。结果显示：学生作答量表所得分数与作答参照工具所得分数的相关系数为0.86（p＜0.05）。

4 讨论

4.1 量表的结构

学习策略结构的研究经历了一个从二维结构向多维结构发展的历程。早期的学习策略由一般策略和调节策略构成，二十世纪九十年代伊始，元认知理论开始融入到学习策略当中。 1994 年，Dembo 根据信息加工及元认知理论，提出学习策略包括认知策略和元认知策略（杜晓新，冯震，1995）。随后Mckeachie 将学习策略划分为认知策略、元认知策略、资源管理策略三个主维度（陈琦，刘儒德，1997）。随后又有学者提出多维结构，例如Gagne 基于对学习者学习过程的考量，将学习策略划分为注意策略、思索策略、记忆策略、编码策略、检索策略（张庆林，1995）。国内学者在学习国外研究成果的同时，结合国内实际情况进行了大量的研究工作。如刘电芝（2003）、杜大源（2007）、曹一鸣与陈鹏举（2018）认为数学学习策略是由数学认知策略、数学元认知策略、数学资源管理策略构成的。

根据前期关于数学学习策略与测评工具的研究，结合我国小学高年级学生数学学习的特点与实际，研究将小学高年级学生数学学习策略的结构定义为三个主维度：数学认知策略、数学元认知策略、数学资源管理策略。根据三次样本预测的结果，小学高年级学生数学学习策略结构稳定为上述三个主成分，这与研究预设的结构相吻合，与初中生数学学习策略调查问卷（王光明，刘丹，2017）、高中生数学学习策略调查问卷（王光明，廖晶，黄倩，王兆云，Mc-Dougall，2015）的维度划分也一致，体现出数学学习策略三维结构划分的稳定性。

在各主维度下的子维度结构方面，研究认为数学认知策略包含三个子维度：复述策略、精加工策略、组织策略。数学元认知策略包含三个子维度：计划策略、监控策略、反思调节策略。数学资源管理策略包含四个子维度：时间管理策略、环境管理策略、心境管理策略、外界求助策略。其中认知策略的划分方式与曹一鸣和陈鹏举（2018）的研究相同，但与刘电芝（2003）的分类方式（概念学习策略、计算学习策略、解题策略、几何知识学习策略）存在差异，其可能原因在于刘电芝的认知策略分类是以数学知识为划分依据，而本研究侧重以知识习得过程中使用的策略。元认知策略的划分方式与以往研究的分类方式基本相同。资源管理策略的划分方式相较于曹一鸣与陈鹏举（2018）的分类增加了环境管理策略。Rose等（2018）指出，关注策略分类而忽视策略的使用环境是语言策略研究近年来备受质疑的原因。因此，增设环境管理策略的考察十分必要。

4.2 量表的信效度

在检验量表内部一致性时，一般认为Cronbach’s α 系数达到 0.60 以上就可接受（吴明隆，2010）。采用 Cronbach’s α 系数检验小学高年级学生数学学习策略量表的信度，研究显示三个主维度以及总量表的 Cronbach’s α 系数分别为0.88，0.90，0.83，0.94，表明各主维度与总量表均具有较好的内部一致性。

在效度检验方面，构建量表的理论框架和编制项目时，研究团队多次讨论，对题目的表述进行分析和修订，反复评估各项目及因子的适当性，以增强量表的内容效度。根据心理测量理论，一个量表的总分与各因子得分的相关系数可以作为检验其内容效度的指标（Foster ＆ Cone，1995）。本研究中问卷总分与其三个主维度得分之间均有较强的相关性（r＝0.76－0.83），表明量表具有良好的内容效度。验证性因素分析表明，该量表的一阶10 因子二阶3 因子模型拟合良好，其中 χ2／df＝3.92，RMSEA＝0.08，NFI＝0.97，TLI＝0.95，CFI＝0.98 和 GFI＝0.97，表明所测数据可以较好地拟合所设模型，问卷具有较好的结构效度。此外，研究选用PISA2012 学生学习策略问卷作为效标，测得所编量表总分与效标量表总分之间相关系数为 0.86（p＜0.05），表明所编量表具有良好的效标效度。

4.3 与以往量表的比较

问卷继承了王光明团队已有量表中的数学学习策略结构模型，同样将数学学习策略划分为数学认知策略、数学元认知策略和数学资源管理策略三个主维度。与以往研究相比，在以下两个方面存在差异：

首先是题目的数量。由于小学生注意力集中时间相对较短，为尽可能避免小学生由于答题时间过长造成数据失真，相较于以往量表的题目数（初中生数学学习策略调查问卷含35 道，高中生数学学习策略调查问卷含51 道）而言，控制了本量表的题目数量，仅有 30 道。

其次是选项的设置。已有的初、高中生数学学习策略量表均采用李克特五点计分，国内现有的量表也多采用五点或七点计分方式。但已有研究显示，四点或六点计分方式可改善量表的区分能力（风笑天，2013）。并且考虑到小学生的答题时间不宜过长，因此本量表采用选项数更少的四点计分，每道题目的四个选项分别为：非常符合、比较符合、比较不符合、非常不符合。