渗透数形结合思想，促学生思维发展

顾丽滨

摘要：“数”与“形”反映了事物两个方面的属性。数形结合，主要指的是数与形之间的一一对应关系。数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，通过“以形助数”或“以数解形”即通过抽象思维与形象思维的结合，可以使复杂问题简单化、抽象问题具体化，从而实现优化解题途径的目的。

关键词：小学数学;数形结合;概念形象化;概念直观化

我国著名数学家华罗庚说过：“数形结合百般好，隔裂分家万事休。”在小学数学学习中，数形结合是经常用到的思想方法，数形结合方法的实质是将抽象的数学语言与直观的图形结合起来。利用数形结合的方法可以使某些抽象的数学问题直观化、生动化，把抽象难理解的问题变为直观形象简易化的问题，有助于把握数学问题的本质;另外，由于使用了数形结合的方法，很多问题便迎刃而解，且解法简捷。

一、渗透数形结合思想，有助于理解数学概念

小学数学的教学内容充满了抽象化的数学概念，这种情况的出现就使得教学的过程过于枯燥，而学生在这一过程中往往会因为难以理解相关的知识点而出现厌烦的心理，继而导致学习效率的降低。在小学数学概念教学中，如果能够建立抽象的数学概念与形象的图形之间的联系，把数学概念中最本质的属性用恰当的图形演示出来，将数和形结合起来，就可以丰富学生的感性材料，为建构数学概念奠定基础。通过以形悟数，将抽象的内容具体化，能帮助学生更好地理解数学概念。

（一）概念形象化

在教学正方形周长公式时，教师先将长方形缩小为正方形，引导学生观察正方形的特征，并尝试求出正方形的周长。学生进而提出求解正方形周长的几种方式，如“一条边长乘4”“四条边长相加”“边长加边长再乘2”，再组织学生对此进行探讨。如此一来，学生则可以更准确地了解正方形周长的概念，在实际运用中也可以基于需要使用不同的方法。

（二）概念直观化

例如，在“正数和负数的初步认识”相关内容的教学中，教师可以先出示情境图，让学生辨别方向。师：小华如果向东走2千米，到达邮局。小林如果向西走2千米，到达公园。师：如果把向东走2千米记作+2千米，那么向西走2千米可以记作什么？课件再展示表示东西方向运动的路程线段图，让学生思考哪里可以标上0，小华与小林的位置大概在哪儿，怎么表示？师再问：看了线段图，你有什么发现？（板书：正数都大于0，负数都小于0）而在这一过程中学生深切感悟数形结合思想的助益，数形结合思想也渗透于学生的数学学习之中。

二、渗透数形结合思想，有助于理解算理

计算在小学教学内容中占相当多的部分，计算教学首先要引导学生理解算理。在教学时，教师应以清晰的理论指导学生理解算理，在理解算理的基础上掌握计算方法，正所谓“知其然，更要知其所以然”。

（一）利用简图帮助学生理解算理

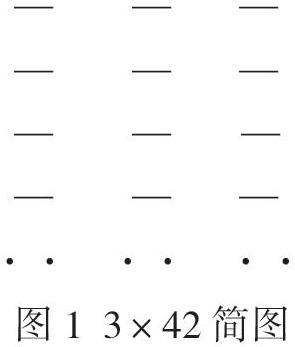
在沪教版数学三年级上册“用一位数乘”的教学中，笔者在新授课的设计中为了让学生更好地理解算理，渗透数形结合的思想方法，通过简图将直观图像和数学语言充分结合起来，帮助学生更好地理解数学知识。如图1所示，笔者用简图表示3×42。其中，一个短横代表的是10，一个小圆点代表的是2。

师：如何在简图上圈一圈，把算式表示出来？

圈法一：所有的短横圈在一起，表示3×40;所有的小圆点圈在一起，表示3×2。

圈法二：一组一圈，表示3个42相加，即3×42。

教师根据简图出示：

3×42=（    ）

3×40=（    ）

3×2 =（    ）

（  ）+（   ）=（    ）

在教学过程中，教师可使用直观图形辅助教学。学生在学习的过程中通过圈一圈、写一写，从而理解乘数是一位数乘法的算理，掌握算法。

（二）数形结合促学生掌握算法

以沪教版数学五年级上册“小数乘小数”这一章节中“小巧搬新家啦！她的房间长4.1米，宽3.2米，小巧房间的面积有多大？”为例。

算法一：

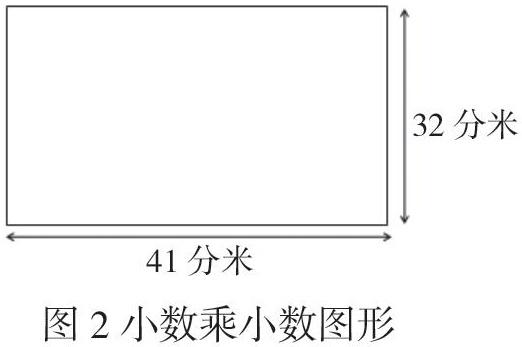
結合题目要求：把4.1米、3.2米转化成以分米为单位，求出面积后，再把平方分米转化为平方米。绘制出相对应的长方形图示（如图2所示），再结合图形进行运算。这样，学生既能够清晰地理解题目内涵，也能够根据图形计算，不容易出错。

4.1米×3.2米=13.12平方米

41分米×32分米 = 1312平方分米

4.1×3.2 = 41×32÷100 = 1312÷100 = 13.12

算法二：把它放在方格图上，通过数格数进行计算。

学生学习、理解和掌握“数的运算”内容时，都要经历从抽象到具体、从感性到理性的过程，这就需要教师在教学过程中不仅要关注结果、关注方法，还要关注得到结果、方法的思维过程，这个思维过程就是学生理解算理、掌握算法的过程。算理的抽象和算法的直观形成了鲜明的对比，在低年级段计算教学中，教师通常用小圆片等学具来组织学生的学习活动，从而把算理形象化、具体化，而到了高年级段，抽象的逻辑思维成了大多数学生的思维特点，此时，学具的应用逐渐由符号、示意图及空间想象等代替。数形结合的思想则帮助学生清晰每一步算的是什么，明白这样计算的道理在哪里，有效沟通新旧知识之间的联系，形成知识串。

三、渗透数形结合思想，有助于解决问题

数形结合思想能够帮助学生透过问题表象认知问题实质，学生的想象力、思维能力等被调动，因而能够从多个角度出发考虑问题。尤其是在应用题的教学中，教师渗透数形结合思想进行教学，可以帮助学生巧妙地将数量之间进行关联，而数量关系作为数学问题的基本特征，也是学生科学解决数学问题的关键。

教材中常常把抽象的问题置于直观的情境中，在直观图示的引导和教师的启发下，学生就能比较容易地理解各种数量之间的关系，从而有效提高学生比较、分析和综合的思维能力。在解决问题这一部分，可以根据数学问题指导学生借助线段图来理解题中的数量关系，从而化繁为简，事半功倍。

（一）帮助学生直观理解数量关系，从而使解题过程简单化

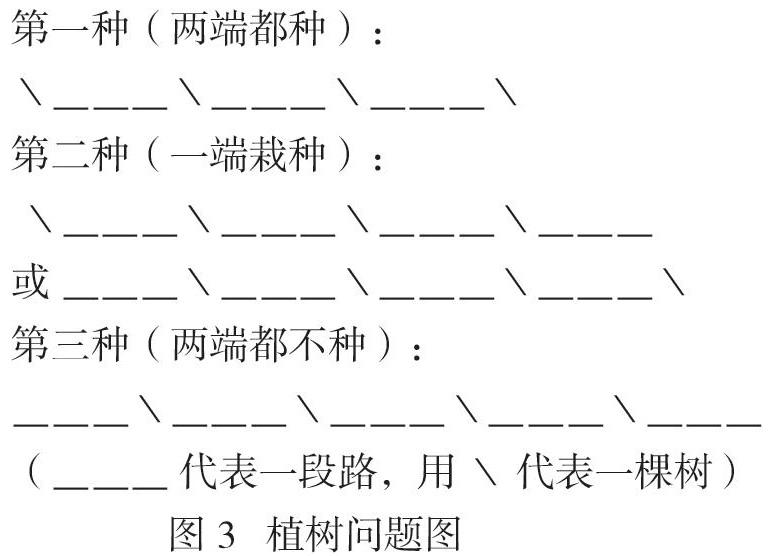
如植树问题，教师可让学生想象：在道路两旁种上四棵树，能有几种种法？学生独自操作完成后，教师根据学生的反馈相应地把三种情况都贴于黑板（如图3所示）：

师生共同小结，得出以下结论：（1）两端都种的情况下，棵数 = 段数 + 1; （2）一端栽种的情况下，棵数 = 段数;（3）两端都不种的情况下，棵数 = 段数 - 1。

一图抵千言。数形结合，抓住了数形之间的关系，帮助学生直观地理解某些数量关系，进而解决数学问题。画出线段图，这种关系就显现出来了，也就找到了解决问题的路径。

（二）帮助学生分析数量关系，明确解题思路

1.借助线段图、示意图读懂题意

教学中的问题，大多以纯文字表述，看上去枯燥乏味。学生平时看多了直观的图形，其抽象思维能力相对被削弱了，他们遇到纯文字的问题，读不懂题意，缺乏解题的自信，更有学生不愿读题、懒得读题。这时就需要借助于图形，让图形来架起学生形象思维和抽象思维之间的桥梁。用画图法是提高理解、分析问题能力的第一步，就是借助线段图或实物图把抽象的数学问题具体化，还原问题的本来面目，使学生读懂题意、理解题意。读懂题意、理解题意是解决问题的第一步，只有读懂题意，学生才有信心解题。所以借助线段图、示意图帮助学生理解题意是本课题至关重要的一步，它是学生打开解决问题大门的一把“金钥匙”。

以相遇问题为例：

沪宁高速公路全长约270千米，一辆轿车和一辆客车分别从上海和南京两地同时出发，相向而行，轿车平均每小时行100千米，客车平均每小时行80千米，经过几小时两车在途中相遇？如图4所示。

在教学中，教师可以让学生收集信息，并进行讨论，逐步出示线段图：

题中有几个物体在运动？（两个物体）以怎样的速度运动？（轿车平均每小时行100千米，客车平均每小时行80千米）

运动的方向与结果各是怎样的？（相向而行;相遇）

要解决一个怎样的数学问题？（几小时相遇？）

你还有什么信息要补充吗？（全长270千米，相遇点在哪儿？）

根据线段图说一说等量关系。（轿车行的路程+客车行的路程=相距的路程）

由此可见，借助线段图，学生很容易理解题目的数量关系，从而解决问题。

2.借助线段图、示意图，提高问题的分析能力

小学生年龄小，理解能力、分析能力都有限，线段图不仅能帮助学生读懂题意、理解题意，还能使题目中的数量关系更明朗，更形象、直观，教学中能帮助学生厘清思路，分析数量关系。

以和倍问题为例：

蝴蝶、蜻蜓和蜜蜂共有180只，其中蝴蝶的數量是蜻蜓数量的2倍，蜜蜂的数量是蜻蜓数量的3倍。三种昆虫各有多少只？

有三个量，怎么找出倍数关系呢？（可引导学生画图，如图5所示。借助图形比较得出一倍量和几倍量的关系）

等量关系是什么呢？

学生迎刃而解：蜻蜓的只数+蝴蝶的只数+蜜蜂的只数=总只数

一图抵万语。数形结合，抓住了数形之间的关系，帮助学生直观地理解某些数量关系，进而解决数学问题。

总而言之，在小学数学教学中，基于学生的认知规律，在教学中渗透数形结合的方法，是对学生数学思维能力的综合培养，也是发展学生逻辑思维能力的良好契机。教学实践表明，数形结合的思想方法可以把抽象的数学知识变得更加直观、具象，有利于学生更好地理解数学知识。同时，数形结合思想提高了学生解决问题的能力，有效地促进了学生思维能力的提升。所以，我们应该在小学数学教学中大胆地探索与实践数形结合思想方法的应用，让我们的数学课堂更精彩！

参考文献：

[1]董丽君.谈谈“数形结合”[J].湖南工业职业技术学院学报，2007（02）.

（责任编辑：奚春皓）