深化数学理解 提升运算能力

杜紫红

运算能力是数学能力的核心要素，小学生数学能力的培养与提升离不开数学运算能力的培养及建构。在运算意义、算法算理的教学与培育过程中，其实也灌输着抽象、推理、建模等数学思想，这一过程有利于学生数学能力及数学思维发展的可持续性。然而，随着社会高度发展，学生学习渠道增多，对于运算内容的学习，常出现学生知其然，不知其所以然的现象。学生跨越式地获得运算算法及结果的同时，却缺失了在建构算理算法的过程中对于数学思想方法的体验。在这样的现实背景下，对于数学运算，学生究竟要学习什么，才能真正体验到数学学习的本质，深化数学理解，提升其运算能力呢？笔者认为，可以从以下三个方面进行思考。

一、悟算理，以理促法

教学中，要注重学生对基础知识、基本技能的理解和掌握，要使学生掌握技能操作的程序和步骤，还要使學生理解程序和步骤的原理。可见，运算中算法的掌握是建立在理解算法的基础上。学生在数学学习过程中，不仅要知道正确的计算方法，更要理解计算的原理，在算理的指引下通过思考、提取、建构来掌握算法，从而形成一定的计算技能。

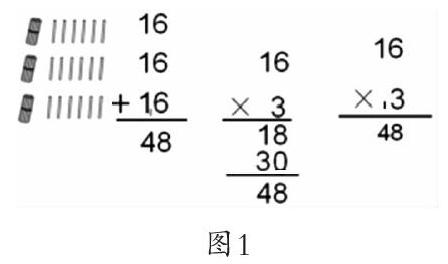
如人教版三上“两位数乘一位数（进位）”的教学，有些学生在课堂教学前就知道笔算的方法，但是主要以模仿的方式进行笔算，并不能主动将算理和算法联系起来。教学中，如何引导学生在理解算理的基础上掌握算法呢？笔者在学生自主表达笔算过程后提问：“16×3的个位上的3已经和6乘了，十位上为什么还要1×3+1，加的1是什么意思？”通过问题聚焦于为什么加“1”，引导学生比较直观图、加法算式、乘法算式（图1）的差异，学生观察并思考后得出：16×3的算法其实和加法中的连加计算一样，先算个位上的3个6相加，就是6×3等于18;再算十位上的3个10相加，就是十位上的1×3等于30;最后18和30再相加，写在乘法竖式里，可以有简便的写法，也就是个位上先写8再进上“小1”，十位上1×3再加1。可以发现，借助引导性问题将学生的思维聚焦在算法形成的薄弱处，能促使学生主动地将原本抽象的算理同加法竖式计算、乘法竖式计算与小棒图建立实质联系，理解6×3、1×3、1×3+1的意义，进而深刻理解乘法笔算的过程，抽象形成结构相对稳定的算法。

心理学研究表明，儿童的认知遵循“感知-表象-概括”这一规律，学生学习的过程需要在直观的计算与观察对比中慢慢感知、逐步体验，从而获得对事物的相对完整的认知。在数的运算教学中，应引导学生在直观感知、形成表象、抽象概括的基础上逐步体验、理解算理，进而掌握算法，只有经历这样的学习过程，才能使得算法的形成有丰富的学习经验的积累及支撑，通过悟算理，以理促法。

二、明思想，明晰学法

数学思想不同于数学知识技能的教学，它以数学知识为载体，是对数学知识探究过程的抽象、提炼、概括和升华。计算教学中，很多内容都需要借助具有方向性的问题引导，帮助学生感悟数学思想，实现迁移学习。

如教学人教版一上“9加几”的内容，在学生学习9加几的计算方法后，笔者出示题组：9+9、9+8、9+7、9+6、9+5、9+4，然后引导学生观察、思考，看看谁能发现藏在题组中的小秘密。学生通过观察发现：这些算式从小到大排列，后面一个算式的得数都比前面一个算式的得数多1;9+6从6借了1，9+8从8借了1……每次都是从后面一个加数中借了1，计算9加几变成10加几来算比较快。甚至有学生发现9+9、9+8、9+7的每个算式得数个位上的数字都比第二个加数少1。那为什么会这样呢？笔者引导学生再次观察算式，学生发现：原来每一个算式中得数个位上的数字少“1”，是被9借走的“1”，计算9加几其实就是计算9加几的“凑十法”。那么如何引导学生继续深入思考，理解20以内进位加法的基础方法呢？笔者提问：“如果学习8加几、7加几，它们的和要从第二个加数中借几呢？4+9你会借几？”通过这些问题引导学生的思维逐渐走向深入。学生观察不同算式中的和的变化，转变为从算式之间联系的角度进行观察和比较;发现了和与加数的联系，深入体验9加几计算的实质（凑十法）所在。学生联系前面的学习内容思考新的数学知识的走向，得出不管是8加几、7加几，还是4+9，都可以先凑十再计算。

上面的教学，学生在体验相同计算方法中感悟类推思想，通过这些学习过程的思考与体验，可以在潜移默化中形成数学学习的方法，并利用这种方法主动地迁移到其他同类知识的学习。

三、联结构，提升素养

认知心理学认为，认知结构具有整体性和概括性的特点，并且整体性和概括性越强，就越有利于学习方法的保持和迁移。当前小学数学教材大多是把原本整体的数学知识划分成一个个知识点，并分散在不同年级的不同单元，教师根据教材知识点的安排，以课时的方式进行教学。因此，每节课的教学内容大体都是围绕着知识点进行，这在一定程度上割裂了数学知识的整体结构，学生在教材上看不出知识的前后联系及其在一系列知识中的地位。学生在数学学习中，如果能从数学学科结构和单元题材结构的角度进行结构化的知识构建，就能把看似不同，实质却有联系的数学知识整合在一起，形成对数学知识体系的整体认知，提升数学素养。

如人教版三上“口算乘法”的内容，教材中的课例引导学生将整十数乘一位数转化成乘法口诀来解决，可如果遇到更大的数怎么办呢？在教学的初始，笔者为结构化教学埋下伏笔，在学生理解了20×3、200×3、2000×3的算理之后，提出问题：“没有两位数、三位数、四位数乘一位数的乘法口诀，你们怎么计算的？”引导学生将口算乘法及时地转化为几个十、几个百、几个千乘几这一模型，帮助他们沟通口算乘法的算理算法，即20×3=2个十×3=2×3×10，200×3=2个百×3=2×3×100，2000×3=2个千×3=2×3×1000，计算时都可以先计算2×3，再乘上相应的计数单位，它们的计算方法相同，只是最终乘上不同的计数单位。随后，笔者抛出问题：“猜猜看，二四得八能解决哪些计算？”学生探究之后回答出二四得八不仅能解决像20×4、200×4、2000×4一类的问题，还可以解决像22×4、222×4一类的算式。可以看出，通过提问引发思考，巧妙地引导学生利用乘法口诀沟通了整数乘法前后知识的联系，它们其实都是利用乘法口诀进行计算，只是计数单位不同。通过这样结构式的教学，帮助学生沟通前后知识的联系，将数学知识串成线、连成面、构成体，潜移默化地指导学生拓展思维，让学生学会思考，提升学生的数学素养。

（作者单位：福建省厦门海沧延奎实验小学   本专辑责任编辑：王振辉）