An Optimal Control Strategy for Multi-UAVs Target Tracking and Cooperative Competition

Yiguo Yang,Liefa Liao,Hong Yang,and Shuai Li,

Abstract—An optimal control strategy of winner-take-all(WTA) model is proposed for target tracking and cooperative competition of multi-UAVs (unmanned aerial vehicles).In this model,firstly,based on the artificial potential field method,the artificial potential field function is improved and the fuzzy control decision is designed to realize the trajectory tracking of dynamic targets.Secondly,according to the finite-time convergence highorder differentiator,a double closed-loop UAV speed tracking the controller is designed to realize the speed control and tracking of the target tracking trajectory.Numerical simulation results show that the designed speed tracking controller has the advantages of fast tracking,high precision,strong stability and avoiding chattering.Finally,a cooperative competition scheme of multiple UAVs based on WTA is designed to find the minimum control energy from multiple UAVs and realize the optimal control strategy.Theoretical analysis and numerical simulation results show that the model has the fast convergence,high control accuracy,strong stability and good robustness.

I.INTRODUCTION

THIS unmanned aerial vehicle (UAV) is a power-driven,unmanned and reusable aircraft widely used in military and civilian fields,such as geographical mapping,air rescue and military strike,etc.This paper imitates the phenomenon of winners-take-all (WTA),the UAV flight optimal control strategy refers to the selection of the minimum control energy input (called the winner) from given inputs.

In the last decades,the WTA phenomenon is widespread around us.In [1],plants grow rapidly toward the light and eventually dominate.Authoritative experts in animal research believe that [2],in the biosphere,if the animal has no natural enemies,it will eventually rule the forest.In human society[3],once a certain company has reached a certain scale in the market,enterprises that enter the market later will be more difficult if the industry wants to open up the market; finally,the enterprise dominates,etc.In our previous work,a lot of research was done on the WTA model,such as in [4]–[7],In[4],many researches on WTA models have been carried out,and the first distributed protocol to dynamically solve this WTA problem.A continuous-time dynamic model has been proposed [5],[6],which is described by an ordinary differential equation and produces the WTA competition by taking advantage of selective positive-negative feedback through the interaction of neurous viap-norm.In addition,a new recursive neural network model for solving quadratic programming problems has been presented,which has solved the WTA problem [7].However,the WTA model has not been applied to the multi-UAVs coordinated flight optimal control strategy.Therefore,based on WTA model,this paper proposed an optimal control strategy for target tracking and cooperative competition of muti-UAV.

During the past two decades,on the one hand,some research results have been achieved in the artificial potential field path planning and flight speed tracking controller of multi-UAV cooperative flight [8]–[15].For artificial potential path planning,the basic principle is that the motion control of UAV is determined by the attraction of target and the repulsion of obstacle.Moreover,the resultant force of virtual attraction and repulsion is regarded as the virtual control force of UAV,which can realize dynamic obstacle avoidance and target tracking of UAV.Artificial potential field methods have attracted much attention from academia.Therefore,the artificial potential field method has aroused widespread concern in the academic community.In [8],its proposed that an artificial potential field method combined with model predictive control (MPC) is used to improve motion planning.In [9],a sliding surface with artificial potential field step the surface is proposed for nonlinear terminal sliding mode,thus guaranteeing that the artificial potential field function converges to zero in an ideal state.In [10],its introduced that artificial potential field method combined with neural network is a new formation control strategy based on radius integral,which ensures the relative distance constraints between any adjacent agents through artificial potential function.In addition,in [11],the modified artificial potential field (APF)method is proposed for that robot avoid collision with fixed obstacles and reaches the target in an optimal path,etc.However,the above study does not consider the combination of fuzzy control with artificial potential field method.On the other hand,the control law of four-rotor UAV has the characteristics of non-linearity,time-varying,multi-input and multi-output,strong coupling and under-actuation.In recent years,the design of control law for non-linear UAV has become a research hotspot of scholars,such as,precise linearization control [16],adaptive control [17],[18],sliding mode control [19],[20],fuzzy control [21],[22],backstepping control [23]and neural network control [24],[25].such as in[12],the author proposes a synovial fluid control and adaptive tracking control method for position and attitude control of a four-rotor UAV.Reference [13]proposes a double closedloop adaptive global terminal sliding controller composed of motion and attitude controllers.The controller converges the position tracking error to zero in a finite time,avoiding the singularity problem in the traditional terminal sliding mode control (TSMC).Furthermore,a double closed-loop active disturbance rejection control (ADRC) scheme was proposed and applied to the nonlinear,strong coupling and low interference problems of four-rotor UAV systems [14].In[15],a four-rotor UAV robust dynamic surface trajectory tracking controller based on extended state observer has been proposed to estimate the uncertainty of parameters and external disturbances.Using a separate inner-loop or outerloop control method,an extended state observer was constructed to estimate the unmeasurable velocity state and the disturbance when the pose is rotated.The tracking error is reduced by the boundedness of all signals in the closed-loop system.Combined with recent research,the UAV speed control has the characteristics of high precision,strong robustness and fast convergence.Therefore,this paper proposes a double closed-loop control method for UAV control applied to multi-UAV cooperative competition optimal control decision.

Fig.1.The overall framework of optimal control strategy for multi-UAVs target tracking and cooperative competition.

This paper proposes an optimal control strategy based on the WTA model for multi-UAVs target tracking and cooperative competition based on the existing results.Its basic framework is shown in Fig.1.Firstly,based on the artificial potential field method,the artificial potential field function is improved and the fuzzy control decision is designed to realize the trajectory tracking of dynamic targets.Secondly,a double closed-loop UAV speed tracking controller based on finitetime convergent high-order differentiator is designed to realize the speed control and tracking of target tracking trajectory.Finally,a multi-UAV cooperative competition model based on WTA is designed to find the minimum control energy from the multi-UAVs.The contributions of this paper mainly include the following.

1) For the ideal path planning of target tracking based on the artificial potential field method,the fuzzy control rules are designed to solve the local minimum problem and optimize the barrier path.The dynamic obstacles and targets are updated to UAV flight path planning in real-time to realize UAV real-time path planning.

2) For the design of the double closed-loop speed tracking controller,to speed up the tracking speed and ensure the stability of the closed-loop system,this paper adopts the double closed-loop speed control with the inner-loop speed being greater than the outer-loop speed.The other aspect,a finite-time convergent high-order differentiator is designed to derive the discontinuous function and suppress the noise in engineering to the last layer of the differentiator.Simulation results show that the noise in the first derivative of the integral action signal is fully suppressed.Improve the reliability,stability,rapidity and accuracy of tracking.

3) For the optimal control strategy of multi-UAVs cooperative competition,the optimal control model based on WTA collaborative competition is designed to obtain the optimal control scheme.Thus,the optimal control strategy of cost reduction is realized.

The rest of this paper is organized in the following manner.In Section II,the WTA model,the kinetic equation of the four-rotor UAV and the principle of the traditional artificial potential field are introduced.In Section III the proposed optimal control strategy for target tracking and collaborative competition of multi-UAVs based on WTA model.Then,numerical examples for the proposed model are presented in Section IV.The Section V is the comparison and analysis of this model and other models.Finally,concluding remarks are given in Section VI.

II.PRELIMINARY AND PROBLEM FORMULATION

In this section,some relevant existing results are presented and the problem investigated in this paper is described.

A.Continuous-time Nonlinear Dynamic Competition

According to our previous work [26],the dynamic equations of theith UAV is

By superimposing the states of all UAVs,the dynamic equation (1) can be rew ritten as follows:

wherev=[v1,v2,...,vn]T,τ=[τ1,τ2,...,τn]T,the operator“ °” represents the following operational rules:

B.Kinetic Equations of Four-Rotor UAV

The kinetic model of four-rotor UAV has the characteristics of multi-input,multi-output and strong coupling underactuation.According to Lagrange equation,the kinetic equations [27]is as follows:

where the subscript “i” denotes theith four-rotor UAV,[ϕ,θ,ψ]is Euler angles of three postures,representing the roll,the pitch and the yaw,respectively.Therefore,[,,]is angular velocity and [,,]is angular acceleration.[x,y,z]is position vector of UAV in three directions,therefore,is its linear velocity,thenvis its flight speed,is its linear acceleration,τ1is the speed control input,τ2,τ3and τ4are the attitude angle control input,viis the flight speed of theith UAV,τiis the general control law ofith UAV.Ldenotes the distance from rotor endpoint to UAV center of gravity,mis the total mass of the UAV gravity load,IγandKγare the inertia and drag coefficient of each axis,respectively,which γ is the six-DoF (degrees of freedom) of the four-rotor UAV.

C.Path Planning Principle Based on Artificial Potential Field Method

Its basic idea is to design the UAV as an abstract artificial attraction field in its operation,which makes the target object produce “attraction” to the UAV,and the obstacles produce“repulsion” to the UAV.Finally,the movement of the drone is controlled by its combined force.

where [x,y,z]represents the position coordinates of the drone in three directions in the inertial coordinate system.F x(j),F y(j)andF z(j)denote the resultant forceFtol(j) in the directionx,y,zat timej,respectively.κ is the scaling factor.Therefore,Ftol(j) is

where the subscript “o”and “g” denotes obstacles and targets,respectively,F oandF grepresent the repulsion and attraction of obstacles and targets to UAVs,the operator “ ∇” represents gradient (Gard) operation,UoandUgrepresent the repulsive potential field function and the attractive potential field function,respectively.

III.CONTINUOUS-TIME DYNAMIC COMPETITION MODEL FOR FOUR-ROTOR UAV

In this section,the WTA optimal control model based on improved artificial potential field method and double closedloop speed tracking control and the corresponding theoretical analysis are proposed.

A.Ideal Path of UAV Determined by Improved Artificial Potential Field Method

1) Improved Design of Artificial Potential Field Method

To solve this problem,the attraction potential field function is defined as

the repulsive potential field function is defined as:

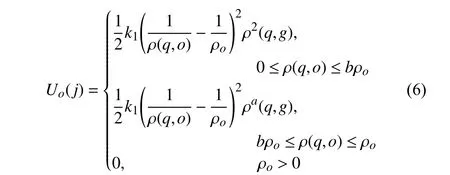
whereqis the position of UAV at timej,ρ(q,g) andρ(q,o)represent their relative distances,ρgis the attraction range and ρois the repulsive range,k0represents the attraction field coefficient,k1represents the repulsive field coefficient,ais gain coefficient,b∈(0,1) is a constant scale factor,when the distance is less thanbρo,the repulsive force field increases and the action intensity increases.

As described in Fig.2(a) show the force analysis diagram of an aircraft under attraction and repulsive forces.The attraction and repulsive functions obtained by calculating the negative gradient of (5) and (6) are as follows:

Fig.2.Schematic diagram of improved design of artificial potential field method.

2) Limitation Analysis of Artificial Potential Field Method

As described in Fig.2(b) show the attraction is greater than the repulsion in a certain time state,and the repulsion is greater than the attraction in the next time state,resulting in multiple cyclic oscillations,or when the resultant forces of attraction and repulsion collide to causeFtol=0,it is called the local minimum phenomenon.To solve the problem,this paper proposed a fuzzy control strategy,so that the UAV quickly leaves the local minimum.Its size iswithwis a positive proportional coefficient,the direction is perpendicular to the line between the current position and the UAV target position,and it satisfies the right-hand rule.The result is shown in Fig.2(c),the design of the fuzzy control algorithm can effectively improve the real-time and selfadaptability of dynamic path planning.

Fuzzy logic control is a simulation of human thinking ability [28].It has the characteristics of strong adaptability,easy adjustment and strong fault tolerance.According to the change of position,the fuzzy repulsion force of the potential field is adjusted by a double-input and single-output fuzzy controller to solve the local minimum value problem.

In the design of fuzzy control,defined ΔΦ is as the UAV angle difference of attraction and repulsion,and domain of discourse is expressed as ΔΦ ∈[−π,π],define ΔFas the difference between the resultant attractive force and the resultant rejection force,and domain of discourse is expressed as ΔF∈[−1,1].ΔΦ and ΔFare fuzzified by single-valued fuzzy method respectively.Its membership function and fuzzy decision-making database are as follows:

a) Input membership function ofΔΦ

b) Input membership function ofΔF

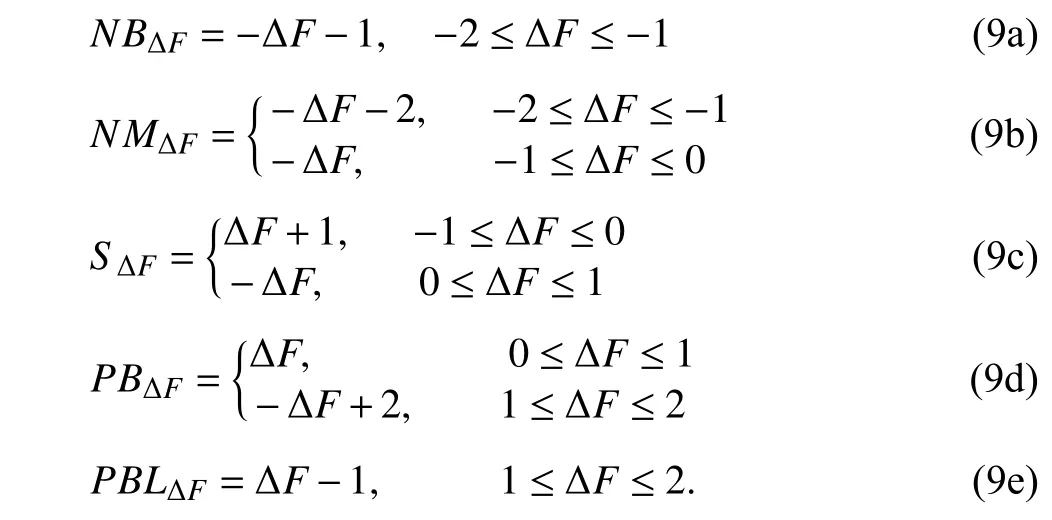
c) Fuzzy decision rules output fuzzy forces

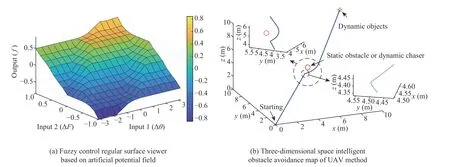
Fig.3.Improved design of artificial potential field method.

Assume that it is required to compare two membership function ΔΦ and ΔF,namely,input linguistic variables beΔΦ is the angle difference of attraction resultant force and repulsion resultant force (as shown in (8)),ΔFis the magnitude difference of attraction resultant force and repulsion resultant force (as shown in (9)).Fuzzy controller outputsf∈[−1,1]fuzzy force,the variables are described with five terms: “negative big” (NB),“negative medium”(NM),“small” (S),“positive medium” (PM),“positive big”(PB).The system of rules for the fuzzy logic is summarized in Table I,the surface viewer is the output force of the fuzzy control as shown in Fig.3(a).

TABLE IFUZZY LOGIC DECISION RULE BASE

As shown in Fig.3(b),the combined force of attraction and repulsion is zero before the UAV approaches the obstacle.The problem of back-and-forth oscillation and local minimum in traditional artificial potential field method can be effectively solved by designing a fuzzy control algorithm.When UAV starts from the starting point and meets obstacles on the way,the attraction equals to the repulsion force,the phenomenon of local minimum will occur,fuzzy control can effectively break the equilibrium state and avoid the phenomenon of local minimum.

3) Dynamic Artificial Potential Field Path Planning

In practical situation,let's consider the case of UAV working in air rescue or military strikes.There are not only static obstacles such as hills but also allied combat aircraft (or its own wingman) or enemy aircraft,radar,etc.This phenomenon can be equivalent to the attraction or repulsion of the UAV caused by multiple dynamic or static objects simultaneously.Let the UAV be subject tom1dynamic attractive,m2static attractive,m3dynamic repulsion andm4static repulsion at timej,the resultant forces of UAV at that time are as follows:

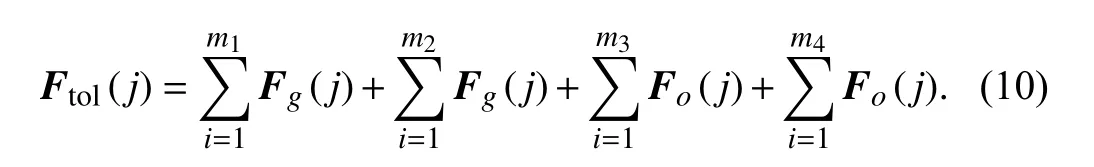
Apparently,the next path coordinate point of the UAV is shown in (4).As shown in Fig.4,the following is obtained:

where θ∗is the angle to theX-Yplane,ϕiis the angle between the projection of resultant forces on theX-Yplane and the positive direction of thex-axis,and with θ∗and φ∗values are determined by attraction and repulsion.

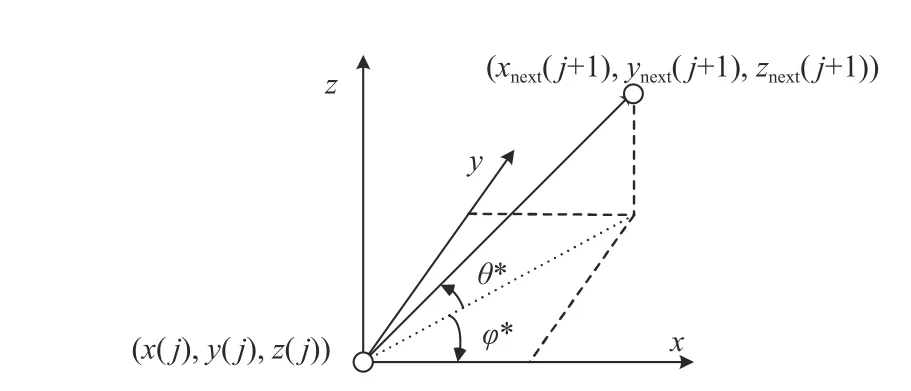
Fig.4.Motion azimuth diagram of UAV.

B.Velocity Tracking Control of UAV Based on Double Closed-Loop

1) Design of Speed Control Law

From the kinetic equations model of a four-rotor UAV as shown in (3),let

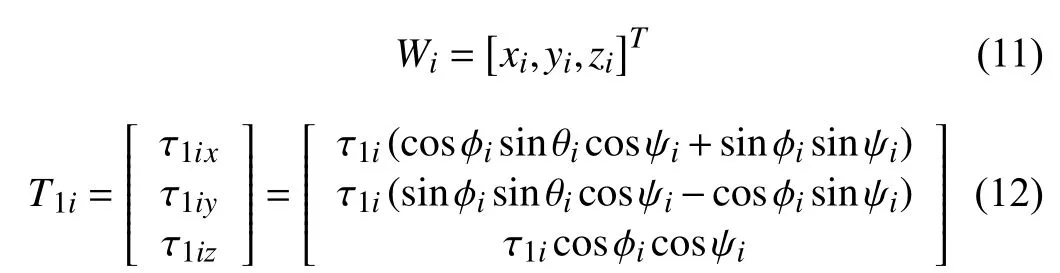
where subscript “i” denotes No.iUAV.Obtained byWas follows:

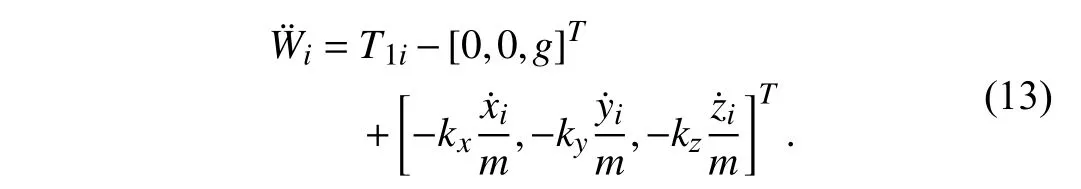
The speed control law is designed as follows:

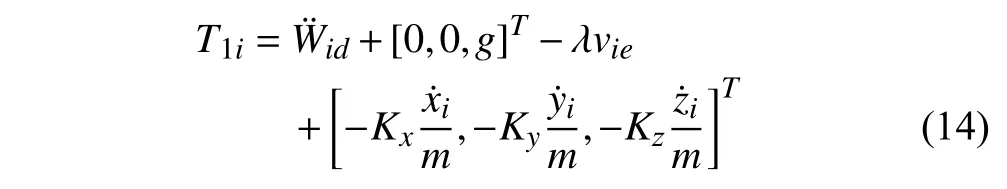
where λ>0,vie=vi−vid,from (13) and (14),the following can be obtained:

Let the Lyapunov function be

ForL,Its derivatives are

As a result

在各功率一定时，随着臭氧发生器出气流量的增大，臭氧的浓度随之减小，这主要是由于流量越小时，氧气在臭氧发生器里的停留时间就越久，有利于臭氧的产生，并且各曲线呈现出斜率相似的趋势，说明氧气的浓度与氧气在臭氧发生器的停留时间基本成正相关，但同时应考虑流量越小时，相同功率下反应器内的温度比更大的出气流量有所增高，会促进臭氧分解，因此，建议出气流量不低于30Nm3/h。与此同时，臭氧的产量却随着流量的增大而增大，这主要是由于出气流量在臭氧产量中所占比重更大，同时由于臭氧浓度与出气流量的变化曲线均为线性，因此，各臭氧产量随流量变化的曲线也呈现出线性关系。

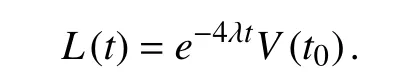
Whent→+∞,there isve→0,according to LaSalle invariant set principle,there is and the exponential convergence,Lyapunov function converges and proves the system’s stability.

2) Solution of State Angle

Because of the four-rotor UAV’s under-actuated characteristics,it’s impossible to track all six-DoF (degrees of freedom) simultaneously.Therefore,the control target scheme of this paper is to track the track and roll angle ϕ in three directions,keeping the elevation angle θ and the yaw angleψ constant.According to (3),let

According to the actual situation,the pitch angle of UAV can not exceed the actual range in θid∈[−90°,90°],otherwise,there will be a crash threat,(17) is derived from (16) as follows:

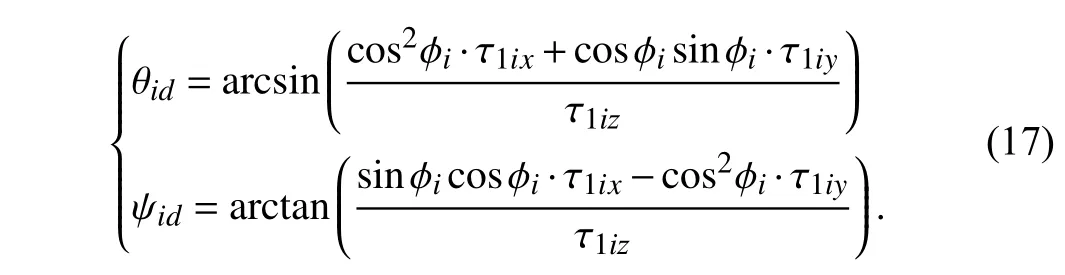
The speed control law is obtained as follows:

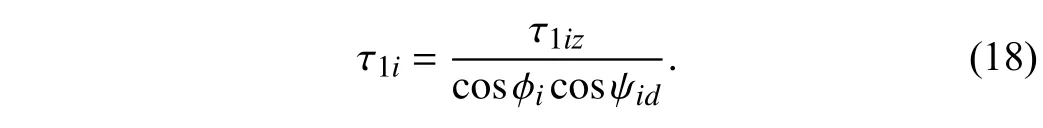
3) Attitude Control Law Design

This paper realizes ϕ→ϕd,θ→θd,and θ→θdby designing the PD control law,let

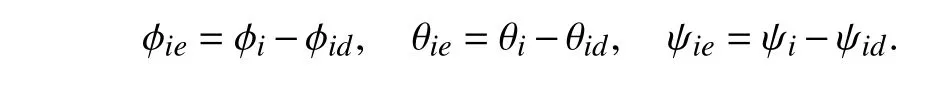
The method of PD control based on feedforward compensation is adopted.The attitude control law is designed as follows:

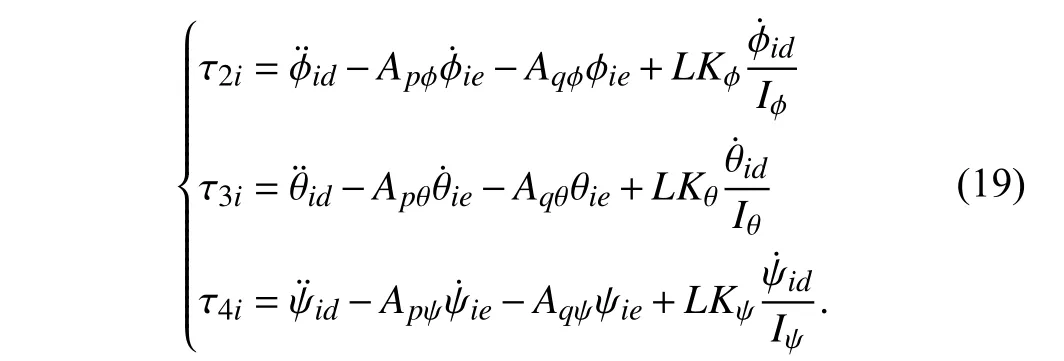
The kinetic equation (3) of the four-rotor UAV combined with (19) can be obtained

Remark 1 [29]:Routh-Hurwitz stability criterion,fornorder systems,the special equation of the system is

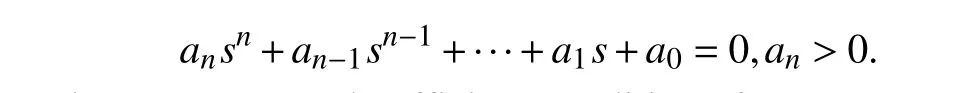
The necessary and sufficient conditions for system stability are as follows:

a) The coefficients of the system characteristic equation are all positive values

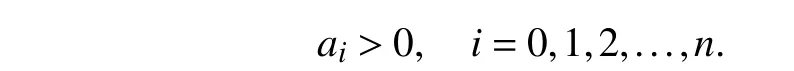
b) The Hurwitz matrix consisting of various coefficients,the subdeterminantsΔ1,Δ2,··· ,Δnof then-order determinant are all greater than zero.where determinant is

According to Hurwitz criterion of the second-order system as shown in Remark 1,Aqγ>0 andApγ+LKγ/Iγ>0 need to be satisfied,where γmeans ϕ,θ or ψ.4) Design and Solution of High-Order Differentiator With Finite-Time Convergence

Lemma 1 [30]:Let there be a higher-order differential equation

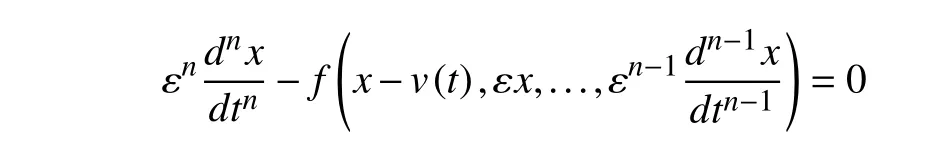
equivalent to

If the following is true:

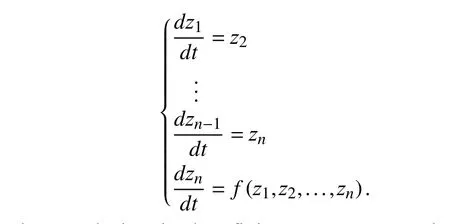
The conclusion is that finite convergence relative to the original point,the result is a variable+1,fori=1,...,n−1,the converges to the derivative of orderiofv(t) infinite time.

According to Lemma 1,design finite-time convergent thirdorder differentiator as shown in(21),realize the tracking solution of ideal pitch angular velocity,angular accelerationand ideal yaw angular velocityand angular acceleration.

wherev(t) is the input signal and can be the ideal roll angleϕdor pitch angle θd,ε is the scaling factor,X1is to track the original input signal,X2is the approximation estimate of the first-order derivative of the input signal,andX3is the approximation estimate of the second-order derivative of the input signal.Let the initial valueX1(0)=0,X2(0)=0,X3(0)=0.

For example,in (21),take the input signalv(t)=5sin(t) and ε=0.04,Simulink simulation results are shown in Fig.5,the designed third-order differentiator can filter the signal,and obtain its first-order and second-order derivatives.In this paper,because the designed differentiator has an integral chain structure,the noise can only exist in the last layer of the differentiator,the signal in the first-order derivative of the integral effect is sufficiently suppressed.Compared with other differentiators,the finite-time convergent differentiator has better convergence speed and stability.

C.Dynamic Competition of Continuous-time Nonlinear UAVs

Designing a group with a total ofnUAVs,in which the dynamic equation of theith UAV as shown in dynamic equation (1).andare the normalized values ofviandτiafter the interval[l,h].The normalized rulesare as follows:

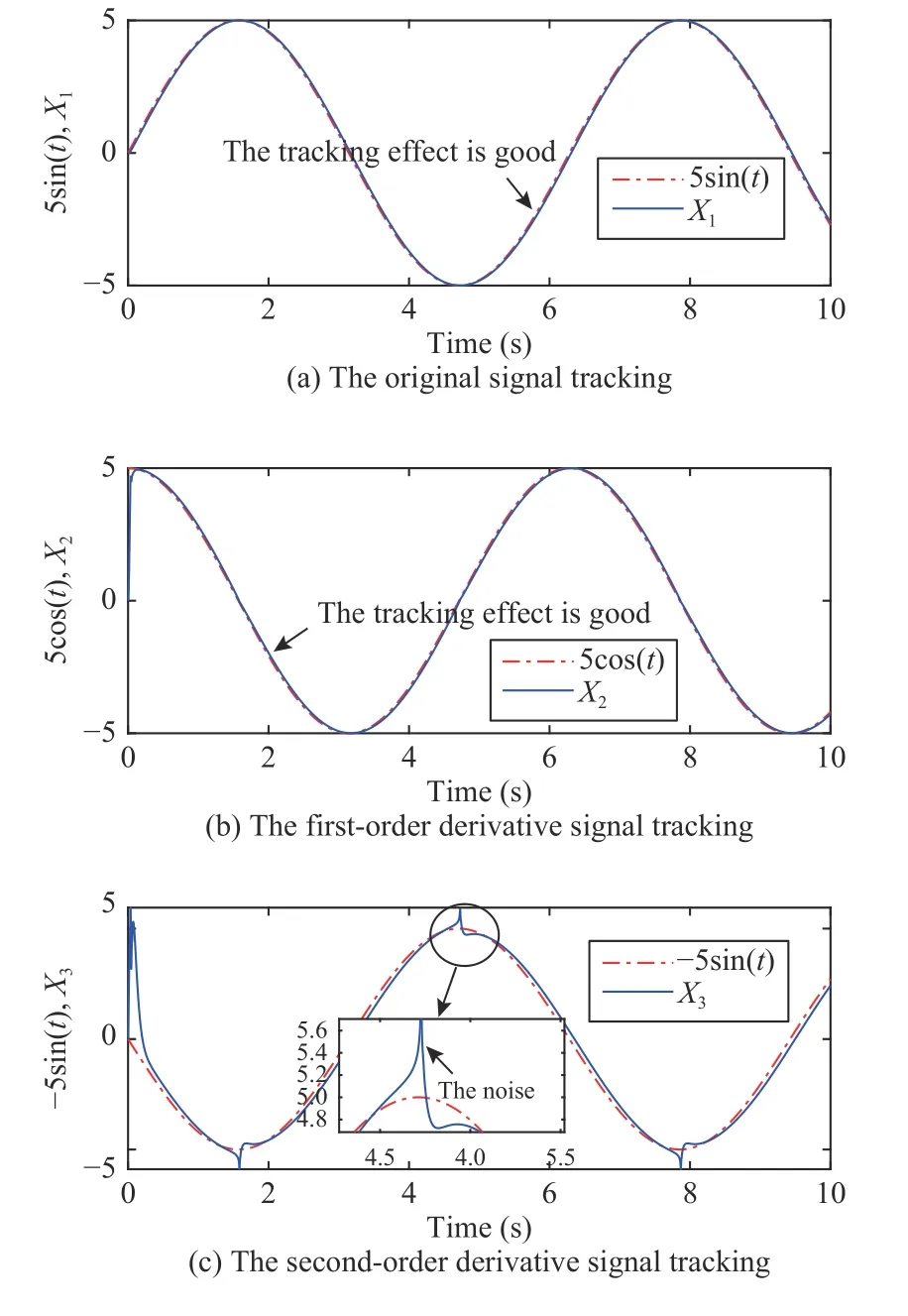
Fig.5.Design of finite-time convergent third-order differentiator.

Remark 2:When,for example,the right side of dynamic equation (1) is zero,but the left side is non-zero,the equation is not established,the differential equation diverges,and the normalized boundary conditionl>0 of the velocity vector is obtained.

Lemma 2 [31]:Let D=Rnbe the domain contains the origin,and ∀t≥0,∀v∈D,L:[0,∞)×D →R is continuous differentiable,satisfaction is as follows:

where α1and α2are class Kfunction,andM(v) is a continuous positive definite function.Letr>0 such that Br∈D,and suppose

Then,there is a class K Lfunction β,and for each initial statev(t0) that satisfies,There are∃T≥0,withv(t0) and µ.The solution of equation=f(t,v)satisfies:

Moreover,if D=Rnand α1belongs to class K∞,(25a) and(25b) are valid for any initial statev(t0) without any restriction on the size of µ.

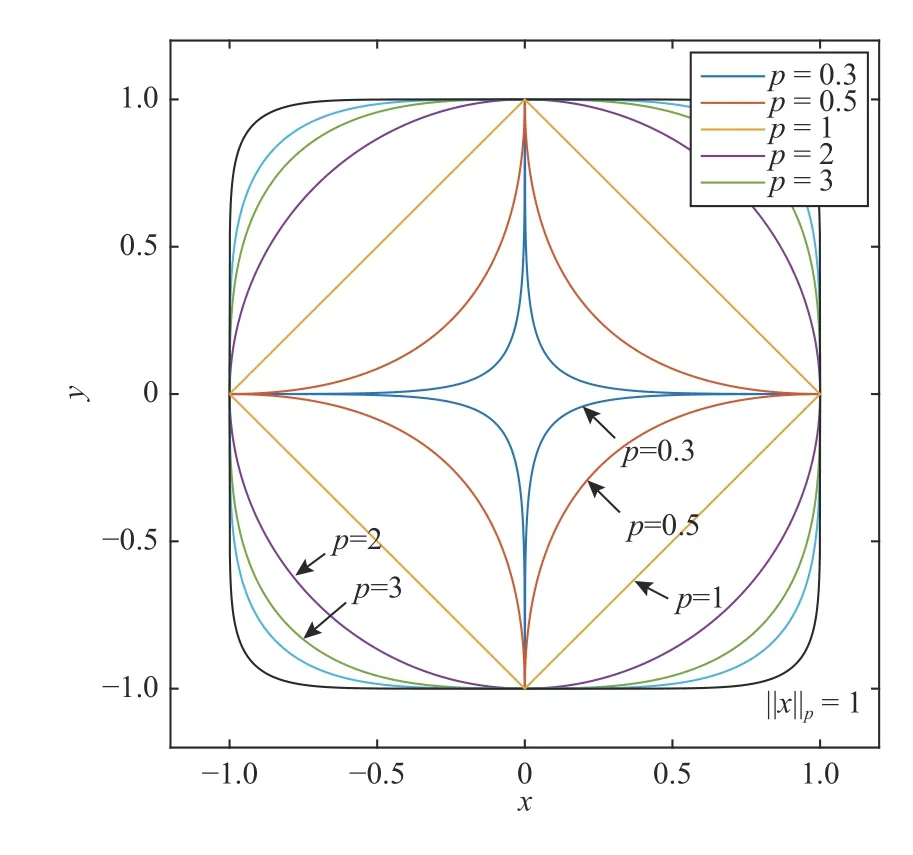
Fig.6.The level set for y=‖x‖p=1 with different value of p.

Remark 3:As shown in Fig.6 isp-norm functiony=‖x‖pcorresponds to different level sets and thus lead to completely different dynamic evolution ofx(namely:v) in dynamic equation (1).

By substituting (22) result into dynamic equation (1),the optimal control strategy of WTA model is obtained as follows:

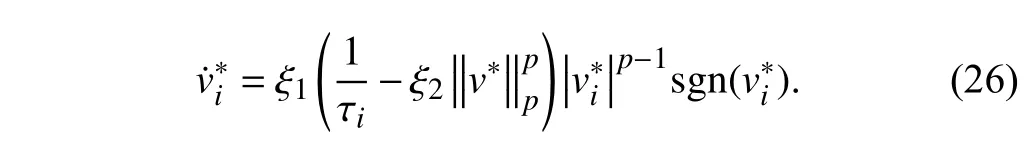
Then (27) can be transformed into

where µ1>0,to ensure the above inequalities (according to LaSalle invariant set principle,Lyapunov function converges and proves the stability of the system),the following needs to be satisfied:

Remark 4:According to Jensen inequality relation,the following inequality relation aboutp-norm is established

wherep1>p2>0,andndenotes the dimension of vectorv(t).

According to Lemma 2,let

Therefore,that

for any initialization of.

IV.NUMERICAL EXAMPLES

This section provides numerical examples to show finitetime non-linear UAV competition based on artificial potential field and double closed-loop speed tracking control.This section mainly simulates and verifies three examples from both static and dynamic static aspects.

A.Simulation Example 1: Multi-UAVs Take-off WTA Competition From Different Take-off Positions at Different Initial Speeds

1) The Ideal Optimal Trajectory Is Generated Based on the Improved Artificial Potential Field Method

Let the tracker take off point (0,0,0),coordinate point(5,5,1.5)((10,10,3) is the terminal point),repulsion range ρo=1 of dynamic obstacle or static obstacle,and attraction range ρg=1 of tracker to the dynamic obstacle,tracked target appeal to tracking target is unlimited.The dynamic or static obstacles are random ly generated by attraction gain factork0=15,repulsion gain factork1=2,gain coefficienta=1/2 proportional scaling factorb=1/2,step size κ=0.1,and the fuzzy control fuzzy force gain coefficientw=100.Dynamic or static obstacles are random ly generated,the effective obstacle points are (1,2,1.5),(2,2,1),(2,2,2),(4,2.2,2.1),(4.1,3,2.1),(3,5,2.1),(4,5,2.1),(5,5,2.3),(5.8,5,2.4),(8,5,2.6),(8.3,6,2.7),(8,8,2.6),(8.5,8,2.7).Because its dynamic obstacles lead to the dynamic pursuit of UAV,the delay effect trajectory of UAV is the ideal trajectory path of UAV as shown in Fig.7(a).

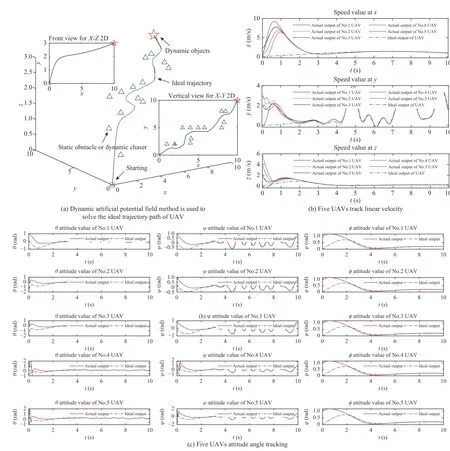
Fig.7.Output results for simulation Example 1.

2) Speed Tracking Control of Double Closed-loop Four-rotor UAV

Considering the actual curve distance of UAV asSiwith respect to time,and the following can be obtained:

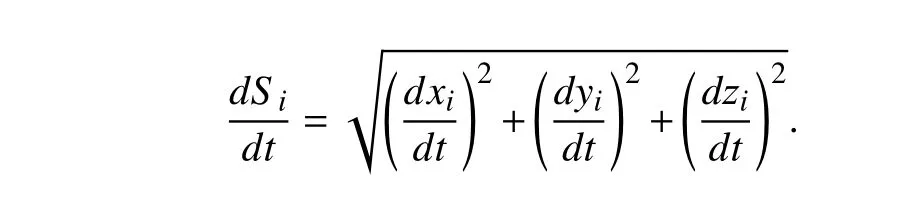
As a result,the flight speed of UAV is

where the subscript “i” denotes theith UAV,,andare velocity vectors at generalized node position coordinate vectors ofx,yandz,respectively.

In the kinetic equations model of a four-rotor UAV,letm=2,L=0.2,g=9.8,Kx=Ky=K z=0.1,Kϕ=Kθ=Kψ=0.015,Iϕ=Iθ=Iψ=1.25.The initial flight attitude is[ϕ,θ,ψ]=[1,1,1],let speed tracking control law proportional factor is λ=3,let state control lawApϕ=Aqϕ=Apθ=Aqθ=Apψ=Aqϕ=1.5.

Let five UAVs start from [0,0,0]at different initial test speeds,v1=[0,0,0],v2=[1,3,2],v3=[2,2,2],v4=[1,3,6],v5=[1,2,4],respectively.The simulation results are shown in Fig.7(b) and Fig.7(c).

As show in Fig.7(b),five UAVs use different speed tracking values to fit the curve at different initial speeds,but finally [x,y,z]three directions velocity tracking approximates the original desired flight speed.Similarly,as described in Fig.7(b),the Euler angles of attitude are similar to the expected values.

The approximate convergence principle is that the high order differential has an integral chain structure.When calculating the derivative of the signal containing noise in engineering,the noise is only included in the last layer of the differential.The double closed-loop speed tracking control is designed based on the principle that the noise in the first derivative of the integral action signal can be suppressed.A double closed-loop speed tracking controller with inner-loop convergence faster than outer-loop is designed,which ensures the stability of the closed-loop speed tracking system and achieves the goal of fast approaching the ideal value.

3) Output Optimal Control Strategy for Continuous-time Nonlinear Static Competition Model

In the model shown in dynamic equation (1),let ξ1=ξ2=1,p=2,andv≥0,the dynamic equation (2) is

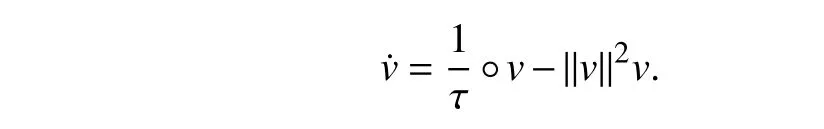
In this simulation,letn=5 is the number of UAV aircraft,this input variables arevi,τiwithi∈{1,2,3,4,5},and it changes dynamically over time with the change of timet,its value is shown in Fig.8(a),whent=0,get

A fter normalization to [0.0100,1.0000],the results are as follows:

B.Simulation Example 2: Multi-UAVs Take-off WTA Competition From Different Take-off Positions at the Same Initial Speed

1) Generation of Ideal Optimal Trajectory

Similar to Example 1,in this section,three UAVs take off at the same initial speed (1,1,1)from position (0,5,0),(0,0,0)and (0,−5,0) respectively,and the initial attitude is (1,1,1).The ideal path trajectory for pursuing the same target is shown in Fig.9(b),where random ly generated static or dynamic obstacles.Because the interaction is dynamic,the graph shows the artificial potential field trajectory after delay processing.

2) Speed Tracking Control of UAV

As described Fig.9(a) shows six-DoF tracking schematic for three UAVs.It can be seen that the tracking effect of six-DoF is better and stable when starting from the same initial test speed and attitude angle and different starting points.The results show that the designed finite-time convergence double closed-loop speed controller has fast convergence speed,high control precision,strong stability and good tracking performance.

3) Optimal Control Output

Simil√ar to Example 1,This paper simulates by normalizingto 0.8.The output of the ideal path planning control law (i.e.,control energy) from the double closed-loop speed tracking controller is [3.2481 × 105,3.4244 ×105,3.6916 × 105].To simplify the simulation normalization to [0.01,1],the simulation results are shown in Fig.9(c),it can be seen that multiple UAVs start from different points of departure (keeping the same take-off speed) to obtain the optimal control strategy of WTA based on the model proposed in this paper.Namely,a strategy of competition and activation between multiple UAVs can finally find the optimal control strategy of UAV control under the same conditions from multiple UAVs.

C.Simulation Example 3: Multi-UAVs Take-off WTA Competition From Different Take-off Positions at Different Initial Speeds

Combined with simulation Examples 1 and 2,in this section,starting from different starting points with different initial velocities.In this simulation,take three starting positions (0,5,0),(0,0,0) and (0,−5,0),and make each starting position take off at the initial speed ofv1=[0,0,0],v2=[1,3,2],v3=[2,2,2],v4=[1,3,6],v5=[1,2,4]using five UAVs respectively,namely,a total of 15 UAVs.In this simulation,letp=1.5,p=2.0,orp=2.5,respectively,other parameters remain unchanged.The simulation is shown in the figure,n=5,whent=0,get

A fter normalization to [0.0100,1.0000],the results are as follows:

Fig.8.WTA competitive optimal model output results for simulation Example 1.

Fig.9.Output results for simulation Example 2.

Fig.10.Comparisons of the UAVs state trajectories in the static competition scenario for p=1.5, p=2, p=2.5 and p=5.

Compared with Examples 1 and 2,simulation Example 3 increases the number of UAVs.The simulation results are shown in Fig.10(b),the winner is No.8 UAV.As shown in the illustration,only one velocity state for the largest UAV inis eventually non-zero(approaching,and other UAV velocity states are suppressed to zero.

As can be observed in Figs.10(a)–(d),in the model of this paper,it takes about 50 s forp=1.5,70 s forp=2.0,90 s forp=2.5,and more than 140 s forp=5,respectively.The comparison of simulation results shows that the smallerpcan achieve faster convergence speed.

D.Simulation Example 4: Output Optimal Supply Strategy of Continuous-time Non-linear Dynamic WAT Competition Model

In simulation Examples 4,based on the multi-UAVs target tracking and cooperative competition model of simulation Examples 1 and 2,the optimal control strategy of WTA model can be obtained.In the first three simulation examples are ideal trajectory planning based on artificial potential field method.The WTA model's input control law (i.e.,control energy) is static for the energy needed to complete the whole operation.

But according to the actual situation,the control energy of UAV in the flight process is dynamic change.In simulation Example 4,an optimal energy supply strategy for four-rotor UAV based on the dynamic form of the model proposed in this paper is modified,namely,the energy consumption produced by the continuous-time multi-UAVs cooperative dynamic competition and the energy supply for UAV entering.The optimal strategy of “refueling” in the air.

Fig.11.Based on simulation Example 1: Continuous time dynamic competitive output.

Our simulation is similar to but different from Example 1,the WTA model is not only a dynamic competition,but also the most energy input is “winner”.Its speed and control energy vary with time,as described in Fig.11(a),all UAVs speed state values and control laws (i.e.,the required energy for control) change with time,through theoretical analysis and numerical verification,It can be seen that: At a certain time,only the corresponding velocity state value of the UAV which controls the maximum energy output is non-zero,and other UAVs are restrained to zero.From the overall analysis,Eventually,the “winner” can be found in real time.Namely,the UAV corresponding to the large energy consumption.

When the interval time is prolonged,the input control energy is counted in 1/5 time,and the actual physical meaning is given.In the actual air combat operations or military material transportation process,assuming that the operational command an aerial refuelling aircraft to “refuel” each of the five UAVs,the output of the dynamic system in the dynamic competition scenario is shown in Fig.11(b),namely,the order of refueling is as follows:No.5 →No.1 →No.4 →No.2→No.3.

V.COMPARISON ANALYSIS

A.Comparative Analysis 1: Path Planning Algorithm Analysis

The classical algorithms [32]based on path planning include artificial potential field,fuzzy annealing,neural network,and reinforcement learning methods.In this paper,the improved dynamic path planning based on the artificial potential field is designed by using the characteristics of small artificial potential field structure and calculation.Firstly,the fuzzy control rules are designed to solve the local minimum problem and optimize the obstacle path.Secondly,the dynamic obstacles and targets are updated to the UAV flight path planning in real time to realize the UAV real-time path planning.

Compared with other path planning [32],the model in this paper has the characteristics of simple structure,small amount of calculation,and effectively avoiding the local minimum value to reach the optimal path planning.Meanwhile,in this paper,a 3D model is built and Simulink simulation is used to verify the advantages of this design: dynamic and real-time update of target and obstacle information,dynamic and realtime cooperative obstacle avoidance and target tracking.

B.Comparative Analysis 2: Speed Tracking Control Analysis of Double Closed-Loop Four-Rotor UAV

Fig.12.Comparison of derivative estimation performance of sliding mode differentiator,linear high-gain differentiator and finite-time convergent differentiator.

For the design of UAV controller,to speed up the tracking speed and ensure the stability of the closed-loop system,this paper designs a double closed-loop speed tracking controller and a finite-time convergence differentiator.The most important factor in the closed-loop system design is the derivation of the intermediate signal generated by the outerloop.This paper compares the performance of the sliding mode algorithm differentiator and the linear high-gain differentiator.

In this paper,to better illustrate the performance of the differentiator proposed in the UAV controller compared with other differentiators,the differentiator design is based on a time-optimal principle [33]– [35]to ensure rapid development convergence.In the simulation,the sinusoidal signal (sin(t)) is selected as the input signal (v(t)),and the initial condition is designed asx1(0)=0,x2(0)=0andx3(0)=0.As shown in the Fig.12,there are oscillations in the output curves of the sliding mode differentiator [36]and the linear high gain differentiator [37],and the output curves of the finite-time convergence differentiator proposed in this paper are smooth.By comparing with other differentiators [36],[37],it is shown that the model in this paper has fast convergence and high precision tracking performance.

C.Comparative Analysis 3: Robustness of Enhanced Noise in Optimal Control Strategy

On the one hand,In the practical implementation of the model proposed in this paper,there are some interferences such as calculation error,quantization error,system white noise,etc.In this situation,the Winner cannot get toexactly.However,when there is additive white noise,the convergence result will still gather near the expected value.

When there is additive white noise,dynamic equation (1)can be reduced to the following:

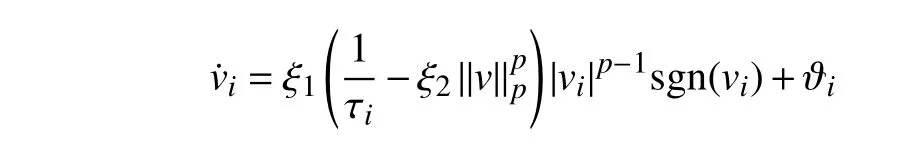
whereϑiis a Guassioan white noise,and its mean is zero and variance isσ2,ϑi≠ϑjfori≠j.

In this simulation,the variance is selected as σ2=0.1,σ2=1 and σ2=10 respectively for the experiment.For differentpvalues shown in simulation Example 3,the simulation results are shown in the Fig.13.It can be concluded that when the additive white Gaussian noise exists,the models in this paper can converge to the expected values,and with the increase of variance,the state values become more and more noisy.Meanwhile,under the same noise,thepvalue is larger and the state value is more noisy.

On the other hand,in practice,the UAV has delayed takeoff.Dynamic equation (1) can be reduced to the following:

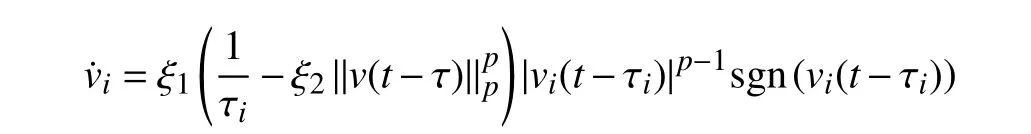
where τi≥0 is the delay constant of state variablev(t).

In this simulation,we choose the delay constant asτi=0.1 fori={1,...,5},τi=0.2fori={6,...,10} and τi=0.3 fori={11,...,15}.The simulation results are shown in the Fig.14.These figures show that it has a non-zero valueeventually,and all the other state values are suppressed to zero.The robustness and reliability of the model hare verified again.

VI.CONCLUSIONS

Fig.13.Comparisons of the UAVs state trajectories of the static competition scenario in presence of Gaussian additive noise under the norm parameter p=1.5 p=2 and p=2.5 and noise level σ 2=0.1,σ 2=1 and σ 2=10.

Fig.14.Comparisons of the UAVs state trajectories in the static competition scenario for p=1.5, p=2, p=2.5 and p=5 with time delay.

This paper proposes an optimal control strategy of the winnertake-all (WTA) model for target tracking and cooperative competition of multi-UAVs.For the ideal path planning of target tracking based on artificial potential field method,by improving the artificial potential field function,the fuzzy control decision is designed to solve the local minimum problem and realize the dynamic trajectory tracking.For the design of double closed-loop speed tracking controller,a highorder differentiator is designed to deduce the discontinuous function and suppress the noise in engineering to the last layer of the differentiator.In order to ensure the stability of the closedloop system,the inner-loop speed is greater than the outer-loop speed.Several simulation examples and comparisons with other models show the performance and theoretical results of the proposed model.Simulation results show that the model has the fast convergence,high control accuracy,strong stability and good robustness.