Blockchain-Assisted Secure Fine-Grained Searchable Encryption for a Cloud-Based Healthcare Cyber-Physical System

Mam ta,,Brij B.Gupta, Senior,Kuan-Ching Li, Senior,Victor C.M.Leung,,Kostas E.Psannis,and Shingo Yamaguchi, Senior

Abstract—The concept of sharing of personal health data over cloud storage in a healthcare-cyber physical system has become popular in recent times as it improves access quality.The privacy of health data can only be preserved by keeping it in an encrypted form,but it affects usability and flexibility in terms of effective search.Attribute-based searchable encryption (ABSE) has proven its worth by providing fine-grained searching capabilities in the shared cloud storage.However,it is not practical to apply this scheme to the devices with limited resources and storage capacity because a typical ABSE involves serious computations.In a healthcare cloud-based cyber-physical system (CCPS),the data is often collected by resource-constraint devices; therefore,here also,we cannot directly apply ABSE schemes.In the proposed work,the inherent computational cost of the ABSE scheme is managed by executing the computationally intensive tasks of a typical ABSE scheme on the blockchain network.Thus,it makes the proposed scheme suitable for online storage and retrieval of personal health data in a typical CCPS.With the assistance of blockchain technology,the proposed scheme offers two main benefits.First,it is free from a trusted authority,which makes it genuinely decentralized and free from a single point of failure.Second,it is computationally efficient because the computational load is now distributed among the consensus nodes in the blockchain network.Specifically,the task of initializing the system,which is considered the most computationally intensive,and the task of partial search token generation,which is considered as the most frequent operation,is now the responsibility of the consensus nodes.This eliminates the need of the trusted authority and reduces the burden of data users,respectively.Further,in comparison to existing decentralized finegrained searchable encryption schemes,the proposed scheme has achieved a significant reduction in storage and computational cost for the secret key associated with users.It has been verified both theoretically and practically in the performance analysis section.

I.INTRODUCTION

CYBER-PHYSICAL systems (CPS) tightly intertwine software and physical components that can have applications in nearly any field we can think of,including healthcare,energy conservation,environment protection,defense,agriculture and many more.CPS tirelessly produce huge silos of data,and to ensure scalability and efficient storage,large companies like Microsoft and Honeywell,etc.,are moving towards cloud-based solutions.Cloud-based CPS(CCPS) improves existing CPS functionalities,but at the same time,presents security challenges.

The data related to healthcare and defense may contain sensitive information.Therefore,in CCPS,in addition to applying security policies at the physical level,there is a need to ensure security at the cyber level,i.e.,the cloud component.The cloud-based CPS for healthcare offers many benefits like monitoring and controlling patient’s health by deploying sensors and actuators in the form of wearable devices.These devices keep track of the essential vitals and may even alert associated medical practitioners in case of critical situations.The data involved in the entire process of monitoring and alerting is highly sensitive,whether it is the location of the patient or the vitals stored by these devices.Therefore,a need for a security mechanism is as essential as providing healthcare services to the patients.Further,the data involved in the continuous monitoring may be massive,and the devices which gather this data are resource constrained.Hence the data is generally stored at a third party cloud server.For this purpose,an obvious solution is to encrypt sensitive data first and then store it to an untrustworthy cloud platform.Encryption indeed ensures security but severely debilitates the accessibility of data.It makes even the most basic operation of searching,a highly challenging task.The searchable encryption (SE) technique is the answer to this problem.

SE enables the cloud server to search confidential data without revealing any information about the data being searched.Further,in the cloud environment,users from multiple domains interact; therefore,access control must be embedded to enable fine-grained searching functionalities.All the stated features in the encryption scheme including search capability and access control fulfills our requirement for cloud-based CPS for healthcare.However,these features come with an inherent cost,and cannot be directly applied for the resource-constraint devices.There is a need of a mechanism to reduce this cost,and this is the key goal of this paper.To enable fine-grained searching capabilities,we have used attribute-based encryption (ABE) and specifically its ciphertext-policy (CP) variant as it makes it possible for the data owners to implement access rule over the encrypted data.Also,the data owner has full control over his shared data which is the essential requirement in any healthcare system.To reduce the associated cost with the ciphertext-policy ABSE scheme,we have leveraged the blockchain technology,where most of the computational load of the ABSE scheme is delegated to the blockchain network.

A.Research Methodology

This section describes the approach followed for the reduction in computational complexity,starting with the problem formulation of the proposed scheme.

1) Problem Formulation

The ABSE scheme provides fine-grained search capabilities to its users but it comes with an inherent computational overhead.In a typical ABSE scheme the associated storage and the computational cost varies linearly with the number of attributes possessed by a user.In a healthcare CCPS,the devices participating in the network are resource constraint.Thus it is not feasible to directly apply the ABSE schemes to access the encrypted information.

Given the above problem,we aim to construct a keyword search scheme with fine-grained search capabilities that can handle a large number of diverse attributes.Furthermore,it should be lightweight enough to be able to be deployed at devices with resource constraints.

2) Proposed Hypotheses

The proposed hypotheses state that the computational complexity of the existing state-of-the art fine-grained searchable encryption schemes is high and also varies with the number of attributes involved in the system.To use such security solutions for devices with limited resources,there is a need to develop a delegation mechanism which can reduce the computational burden from the entities involved in the system.The proposed scheme aims to reduce the associated cost of a fine-grained searchable encryption scheme with the assistance of blockchain technology.

3) Proposed Solution

To address the above-stated problem,in our view,there can be two possible solutions.First,is to make the associated cost independent of the number of attributes.It has already been the focus of many works,like [1]–[4].Second,resourceconstraint devices should not execute computationally intensive tasks involved in a typical ABSE scheme by themselves and leverage other technology like blockchain technology,which can improve both flexibility and reduce system overhead.

With blockchain technology,the proposed scheme can attain the following characteristic features:

Decentralization:It is the key property of blockchain technology,which means that there is no central control,i.e.,there exists no single authority responsible for governing the system.The searchable encryption system developed using the blockchain technology inherits this fundamental property and hence results in a fully decentralized system.

Reduction in computation overhead:In the blockchainassisted searchable encryption system,the task of system initialization is not the responsibility of a single entity.However,it is handled together by blockchain consensus nodes.Furthermore,the task of search token generation is assisted by consensus nodes to reduce the burden from endusers.

Improves system reliability and free from a single point of failure:In the blockchain-assisted searchable encryption system,there is no need for a central authority,and no master secret key is needed to generate user credentials.Hence,this makes the system more reliable in case one or more nodes fails or becomes malicious.

The remaining of this article is organized as follows:Section II discusses related works.In Section III,the reader is enlightened with the essential background required to understand the construction of the proposed scheme.Further,it presents an introduction to the blockchain and other retrospective techniques which forms the basis of the paper.Section IV gives the system and security definitions and explains the system and security model of the proposed scheme.Section V provides detailed construction of the proposed scheme along with its correctness and security analysis.Section VI finally concludes the paper with possible directions for future work.

II.RELATED WORK

ABSE enables fine-grained searching capabilities in a multiuser environment.Several attribute-based searchable schemes have been developed using either of the two design frameworks (ciphertext-policy or key-policy) [1]–[3].Moreover,in the area of healthcare,there exist some attributebased keyword search schemes [5]–[8].However,most of them need a central authority for management and distribution of secret keys to the cloud users.Consider a scenario where a data owner wants to share his data with a large number of users who possess attributes from different domains.Then the single authority cannot efficiently manage such a large and diverse set of attributes alone.Such a scenario is prevalent in the healthcare system,e.g.,in healthcare networks,a data owner,i.e.,a patient may want to share his data with users like a researcher,or a doctor or some insurance agent.All of these users belong to an entirely different domain; hence,there is a need for a multi-authority system where each authority is responsible for the management of a disjoint set of attributes from different domains.

One such multi-authority searchable encryption scheme was recently proposed by M iaoet al.[9].They achieved decentralization by eliminating the central authority.However,the schemes mentioned above,including the one in [9]comes with tremendous computational complexity inherited from the underlying ABE scheme.To reduce this computational overhead and to achieve decentralization at the same time,the authors leveraged the blockchain technology.They delegated most of the computationally intensive tasks either to the blockchain network or to the cloud server.In the proposed scheme,the system initialization and partial search token generation tasks are handled by the blockchain network,while the cloud server handles the search task.Thus,the users can stay relaxed and get their task completed by the smart blockchain technology.There exist several scenarios in literature where blockchain technology has been used[10]–[13].In [14],the searchable encryption scheme has been developed by leveraging blockchain technology,but it focuses on the searchable encryption in the symmetric setting.In [12],a searchable encryption scheme has been proposed with the assistance of blockchain technology in the public-key setting,but they did not consider the fine-grained searching capabilities into account.

III.BACKGROUND

This section gives the necessary information about the bilinear map,hardness assumptions on which the proposed scheme relies,and the structure of the access policy used in the proposed scheme.

A.Bilinear Map and Hardness Assumption

LetGbe a source cyclic group of prime order,p,andGTbe a target cyclic group of same orderpandgbe the generator of the source group,G.Letebe a map betweenGandGT,e:G×G→GT,it is called a bilinear map if it satisfies the following conditions:

1) ∀X=gu∈G1andY=gv∈G2:e(gu,gv)=e(g,g)uvwhereu,v∈Zp.This is called the bilinearity property.

2)e(g,g)is the generator of the target group,GT,ifgis the generator ofG.This property is called non-degeneracy.

3) ∀X,Y∈G;e(X,Y) is efficiently computable.

Assumption (q-decisional parallel bilinear Diffie-Hellman exponent (DPBDHE) ):Lete:G×G→GTbe a bilinear map defined above.Consider another cyclic groupZpof integers of order againp.Chooses,a,b1,b2,...,bq∈Zp,U∈GTand compute the t{upl}eD,whic{h co}nsists of the following elements:

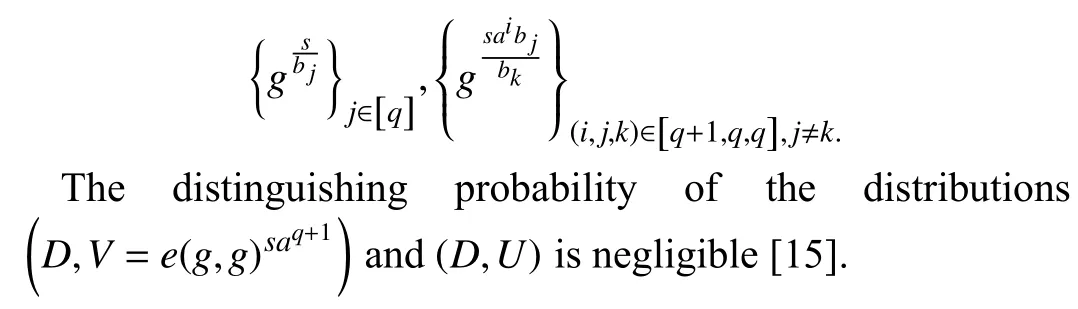
B.Access Structure

To construct the proposed searchable encryption scheme,we have used the monotonic access structure,which is defined as: Let the attribute universe be represented by U.A monotonic access structure,A,on U consists of non-empty subsets of U such that if a subset belongs to A then its superset must also be there in A,i.e.,∀B,C∈A,ifB∈A andB⊆C,thenC∈A [16].To distribute the secret over the access structure we use a linear secret sharing scheme (LSSS),π,overZp,which is defined as follows [16]:

LSSS should satisfy the linear reconstruction property which states that if∃S∈A such thatIrepresents the set of rows(l)such thatρ(l)∈Sthen,given λirepresents the valid shares of secret,s.

C.Shamir’s Secret Sharing Scheme

It is used to divide a secret intonshares such that the secret can only be constructed if a minimum ofkshares is available among them.Therefore,krepresents the threshold because after collectingkshares,the secret can be revealed.It is based on polynomial interpolation,givenkpoints,(xi,yi),such that no two different points have the samex-axis component,and in a two-dimensional space,there exists a single unique polynomial,q,of degreek−1 such thatq(xi)=yi∀i.Thus,the idea is to construct a polynomial of degreek−1,where the data to be shared is placed at the position of a constant term and restof the coefficients are selected random ly,i.e.,q(x)=,whereZpis the group of integers over which the polynomial is constructed.Now,generate thenpoints from this polynomial by putting different values of,i.e.,generate(xi,yi).The secret can be reconstructed by using any of thekpoints among the availablenpoints using the Lagrange interpolation method.To find the coefficients ofq(x),first,find the Lagrange identities by using thesekpoints as follows:

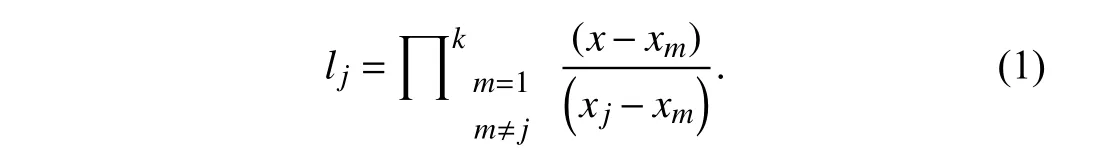
D.Consortium Blockchain Platform and its Role in the Proposed Scheme

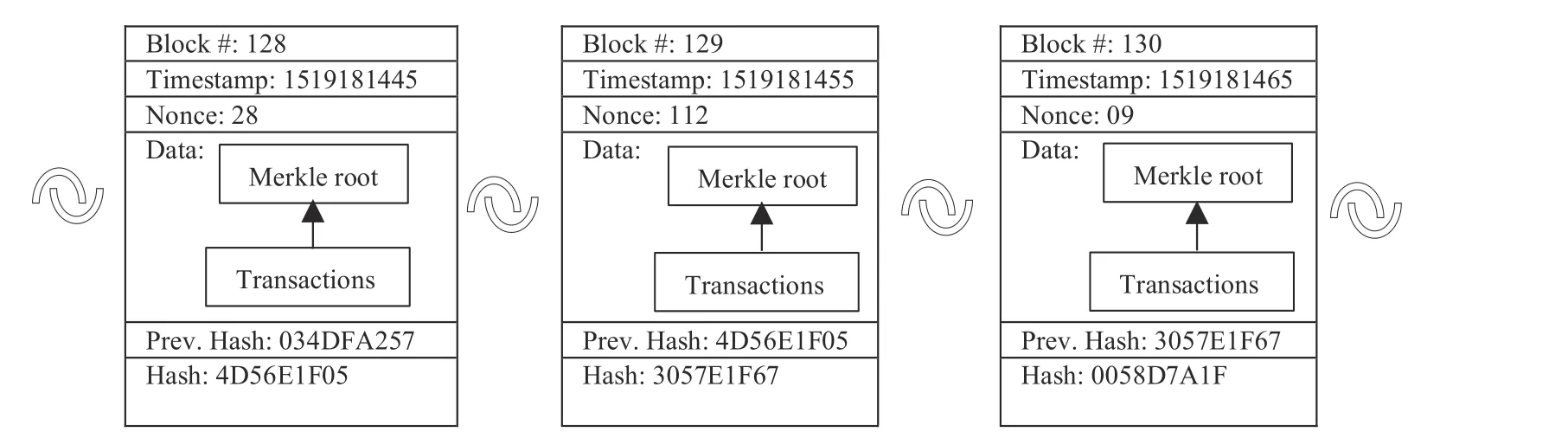
Fig.1.General structure of a blockchain.

The consortium blockchain (CB) platform extends the concept of private blockchain where the entire network is managed by a group of organizations instead of a single organization like in a private blockchain platform [14],[17],[18].A CB platform represents the fine line between public and private blockchain platforms.It adds flexibility in rules to be more like public blockchain.The visibility of the blockchain may be limited only to validators,authorized users or is visible to everyone,thereby combining the features of both the public and private blockchain platforms.The most noticeable difference between both public and private blockchain platforms is observed during the consensus.Unlike the open system in public blockchain or a completely closed system in a private blockchain,in consortium blockchain,a group of equally powered nodes participate in consensus.The typical structure of the blocks and how these blocks are connected in any blockchain platform is shown below in Fig.1.

Blockchain,as the name suggests itself that it is a chain of blocks,and this chain is formed and secured with the application of cryptography.Blockchain can also be defined as a sequence of records which is analogous to traditional ledgers with an additional property of immutability.Hence,it is often called an immutable ledger.Now,depending upon the requirement and application area,the responsibility of managing and updating this ledger is given either to everyone in the blockchain network (public blockchain platform,e.g.,the Bitcoin network [19]),or to one particular organization(private blockchain platform,e.g.,Hyperledger),or to a selected set of users from different organizations with equal power (consortium blockchain platform,e.g.,Quorum).

In cloud-based healthcare CPS,the public blockchain platform does not seem suitable because the public blockchain allow s access to everyone on the system and the data involved in the healthcare CPS may contain sensitive information which is not for the public use.The private blockchain platform also does not fit in the considered scenario because it is too restrictive,and there is still control by one single authority who can manipulate the data for their benefit.Therefore,the option that is suited well for the present scenario is the consortium blockchain where different entities associated with the healthcare CPS makes a consortium and pre-decides the nodes that will participate in the consensus.By leveraging the benefits of consortium blockchain in healthcare-CCPS,one can impose control as well as can enjoy the decided degree of freedom.The architecture of the consortium blockchain used in the proposed scheme is shown in Fig.2.

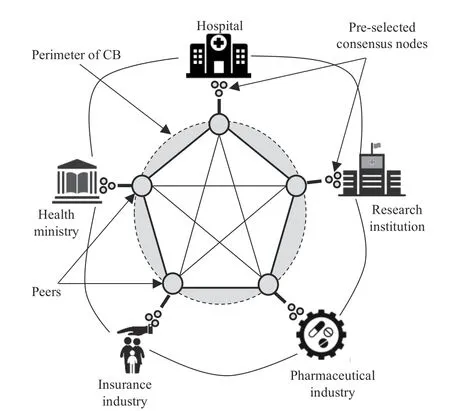
Fig.2.Architecture of consortium blockchain for healthcare CPS.

The consortium blockchain for healthcare CPS may involve entities like hospitals,research institutions,various state and central health departments managed by the health ministry,and the insurance and pharmaceutical industries,etc.These organizations pre-select some of the nodes as the consensus nodes as per their governance policy.These designated nodes are the one which participate in managing and updating the distributed ledger.In contrast,the other nodes can generate or contribute data.If the number of the consensus nodes is increased,then it results in a more secure and fault-tolerant system.Because now more nodes must agree to reach consensus.Further,the system becomes more scalable in terms of the number of transactions processed.Because in the consortium blockchain consensus nodes are the ones who can contribute a new block in the blockchain.The consensus protocol also requires less computational power because the consensus nodes are chosen by the organizations with a high trust level.

Thus,as the number of consensus node increases,there will be an increase in the number of new blocks,and as a result,more transactions will be included for processing.Lastly,as we increase the number of consensus nodes,the degree of decentralization also increases,which results in a more robust system.

Role of CB in the proposed scheme:

1)System Setup:The consensus nodes initialize the system and generate the global public parameters by using Shamir’s secret sharing scheme.

2) User Registration and Generation of Partial Search Token:Any user can register themselves to CB by storing their public key corresponding to their unique global identity.It is also responsible for managing and generating the search token when some user wants to retrieve encrypted information from the cloud,he/she can reach the CB to generate the partial search token corresponding to the attributes possessed by the user.

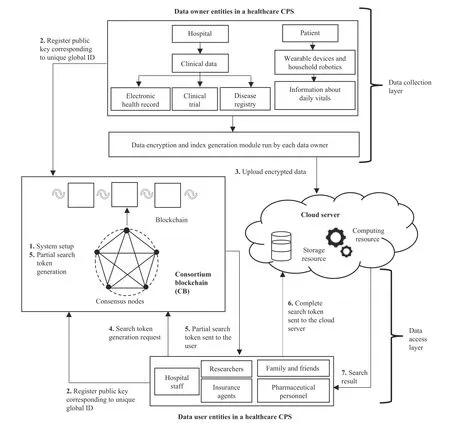
Fig.3.Architecture of the proposed scheme for CCPS.

3)Free From Keeping the Master Secret:In the CB assisted proposed scheme,there is no single entity that manages the system.Hence,it is free from keeping master secret unlike the existing schemes [11]–[14].

IV.SCHEME PRELIMINARIES

This section explains the architecture that provides the general algorithm for the proposed scheme.Further,it gives the security definition along with the game-based security model for the proposed scheme.

A.Architecture of the System

The system is composed of the following four entities,as shown in Fig.3:

1) Consortium Blockchain (CB):This entity will initialize the system and generate global parameters.Further,it registers the public key of the user corresponding to their unique global ID (GID).When a user wants to perform a search,then he/she can reach the CB along with the attributes possessed by him/her and the CB will generate the partial search token for the user.

2) Data Owner (DO):As the name suggests,DO is the one who owns some data (health data in the considered scenario)and wants to share his/her health data to a third-party cloud server.Before outsourcing both the health data file and the associated data,the keywords are first encrypted.In a healthcare system,the data owner is a patient who encrypts his health data using any standard encryption algorithm and probably the symmetric key algorithm (fast computation).The associated symmetric key used for encrypting data and the keywords contained in that data are encrypted using theGen Indexalgorithm of the proposed scheme.

3) Data User (DU):DU is the one who wants to access the data stored at the cloud server.He/she will generate the complete search token which is then sent to the cloud server to retrieve the file containing the searched keyword.In a healthcare system,a data user may be a researcher or a doctor,etc.

4) Cloud Server (CS):CS is the one which stores encrypted health data,performs a keyword search on behalf of the data user and returns the search result.A healthcare provider usually manages it in the considered scenario.

The detailed explanation of various steps shown in Fig.3 is as follows:

1) The consortium blockchain performs system initialization,and the global public parameters are published.

2) The CCPS users (data owner and data user) register themselves on CB by storing their public key generated by them locally,along with their GID.

3) The data owners run theGen Indexalgorithm to generate the ciphertext and upload it to the cloud server for secure sharing.

4) To get the required data from the cloud server,the DU sends a search token generation request to the CB.The search token request contains the global ID of the user,along with his/her set of attributes.

5) In CB,the set of consensus nodes will verify the user’s attributes and generate a partial search token for them using those attributes,which is then sent to the user who requested it.

6) Using the partial search token,DU will generate the complete search token using his/her secret key corresponding to his/her GID.The complete search token generated by DU is then sent to the cloud server.

7) Using the complete search token,CS runs theS earchalgorithm on behalf of the user,and the search result is then returned to DU.

B.Primary Algorithms

The proposed scheme consists of the following probabilistic polynomial time (PPT) algorithms:

1)GPP←GS etup(1n):CB runs this algorithm by taking the security parameter in the unary format as input and generates global public parameters.LetCN={cn1,cn2,...,cnn}be the set of consensus nodes,Att,be the universe of attributes and Wrepresents the keyword space such that each keyword is a binary string.

2)[PKGid,S KGid]←KeyGen(GPP,Gid∈GID):It is run locally by each CCPS user to get their key pair (public,PKand secret,S K) corresponding to theirGid.PKGidis sent to the blockchain andS KGidis kept by the user.

3)C←Gen Index(GPP,(A,ρ),w∈W):It is executed by DU to get the searchable index for the keyword,w.As we are using the CP-ABE design framework,this algorithm takes access structure,A,in addition toGPPto encrypt the keyword.

4)PTK←PTok(GPP,Gid∈GID,S ⊆Att):This algorithm is run by the consensus nodes in the consortium blockchain.It takesGidand the attributes possessed by the user.CB will first verify that the attributes claimed by the user are genuinely his/her attributes by checking the information associated with his/herGid.After verification is successful,then CB will output the partial search token for that user.

5)CTK←CTok(GPP,S KGid,w’):The data user will use this algorithm to generate the complete search token for the keyword,w’,using his secret key credentials,S KGid.

6)0/1 ←S earch(GPP,C,CTK):This algorithm is run by the cloud server on behalf of the data user.It will take the ciphertext,C,and the search token,CTK,of the keyword,w,and performs a search for that keyword without decrypting it.If a match is found then it returns 1 else,it returns 0 and if a user is not authorized to perform the search,then it returns ⊥.

The interaction between different entities involved in the system,along with their role,is shown in Fig.4.The detail of each step shown in Fig.4 has already been given in Section IV-A.

Correctness:The proposed scheme is correct if the following condition holds:

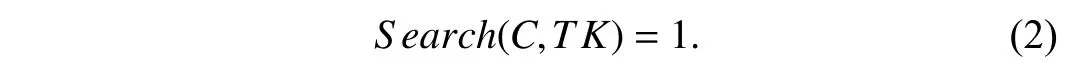
For the givenGPP←GS etup,[LPPτ,MS Kτ]←AAS etup,S KGid←KeyGen,C←Gen IndexandTK←Trapdoor.

C.Security Definition and Model

In this section,we will first define the meaning of security against a non-adaptive chosen keyword attack.Then the security of the proposed scheme is modelled as a game between a challenger,C,and an adversary,A,where challenger tries to break the security by leveraging the adversary’s output.

1) Security Definition

Indistinguishability against non-adaptive chosen keyword attack (CKA): It states that given the two challenge keyword ciphertexts,A should not be able to determine which ciphertext is the encryption of a keyword of their choice even if they gain access to the trapdoors for all the keywords except the challenge keywords.In the non-adaptive security definition,an adversary chooses the consensus nodes to be corrupted after looking at the global public parameters and keeping them the same throughout the game,which can corrupt at mostk−1 nodes.Moreover,the adversary selects the challenge access policy,A∗,which A plans to attack.

The above-stated security definition is modelled as a game between Cand A,with the following phases:

a) Global setup phase:Here,CrunsGS etup(λ) algorithm to get the global public parameters,which are then sent to A.

b) Initialization phase:After looking at the global parameters,a set of corrupted consensus nodes,CNc⊆CN:|CNc|≤k−1,and a set of non-corrupted consensus nodes,CNn⊆CN:(CNc∩CNn)=∅are chosen by A.Further,A selects the challengeaccess policy,A∗.

c) Query phase:Here,A can submit the query for the search token with (Gidi,Si).The queried trapdoors are stored in a list,Ltk,maintained by C.

d) Challenge phase:In this phase,A is asked to choose keywords,{w0,w1}of equal length such that{w0,w1}∉Ltkwhich are then sent to C.Upon receiving the challenge keywords,Cselects a binary bit,b∈{0,1} and generates the challenge ciphertext,C∗,for the keyword,wb,by usingGen Indexalgorithm and the challenge access policy,A∗.The resultingC∗is then sent to the adversary,A.

Fig.4.Interaction Between Different Entities in the Proposed Scheme.

e) Output phase:Here A outputs its guessb′ofband becomes the winner ifb′=bwith the advantage as follows:?

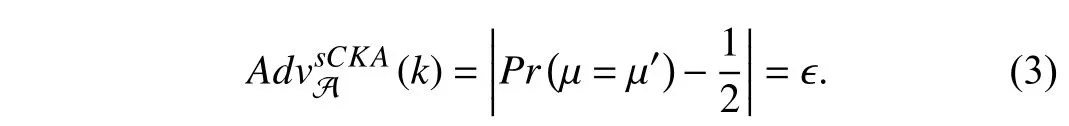
If for all PPT A this advantage is negligible,then the proposed scheme is said to be CKA secure.

V.THE PROPOSED SCHEME

This section discusses the construction of the proposed scheme along with a detailed correctness analysis,security analysis,performance analysis and a comparative analysis with the existing schemes.

A.Detailed Construction

The proposed scheme uses a linear secret sharing scheme(LSSS) and monotonic access structure represented by an LSSS matrix,A.The detail of each algorithm involved in the scheme is given below:

1)GS etup(1n)

The global setup algorithm is run by a set of consensus nodes,CN={cn1,cn2,...,cnn}.It selects a cyclic source group,G,of prime order,p,with a generator,g,and generates a bilinear map,e:G×G→GT,whereGTis a target cyclic group of prime order,p.Let GID be the global identity space,Attbe the attribute universe,and W be the keyword space.Select three collision-resistant hash functions,H1:GID →G,H2:U →G,H3:{0,1}∗→ZpwhereZpis a group of integers of prime order,p,and each keyword,w∈W,is assumed to be a binary string.Select two secrets{α,β}←Zp,and calculate the shares of these two secrets,using Sham ir’s secret sharing scheme(k,n)fornconsensus nodes.Using the secret shares,each consensus node computes the two local public parameters,e(g,g)αiandgβiand broadcast them to the blockchain network.To get the global public parameters,kor more consensus nodes combine their secret shares using the Lagrange polynomial interpolation method as follows:

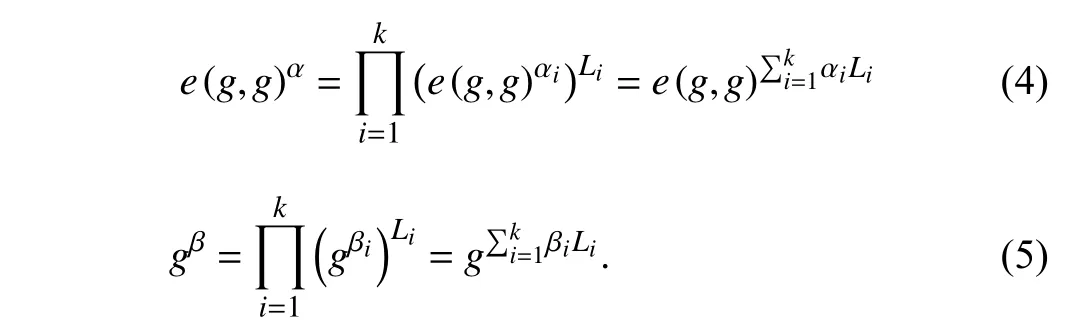
Conse(nsus nodes publish the gl)obal public parameters,GPP=e,p,g,H1,H2,H3,e(g,g)α,gβ.

2)KeyGen(GPP,Gid∈GID)

It is executed locally by each CCPS user to get his/her public and private key pair corresponding to his/herGid.Random ly select,γGid∈Zpand computegγGid.The user then sends the public key,PKGid=gγGidto the blockchain (user registration at blockchain) and keeps the corresponding secret key,S KGid=γGidto himself/herself.

3)Gen Index(GPP,(A,ρ),w∈W)

4)PTok(GPP,PKGid,S⊆Att)

5)CTok(GPP,S KGid,PTK,w’)

6) Search(GPP,C,CTK)

λxcxwill reconstructsandwxcxwill reconstruct 0.λxare the shares of secrets,whilewxare the shares of 0.

Multiply (8) and (9):

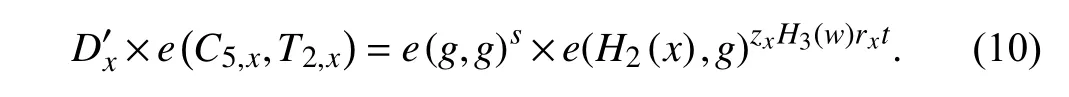
From R.H.S.of (6),compute:

From (10) and (11),(6) holds,provided the keyword in both the ciphertext and the trapdoor are same.

B.Security Analysis

Security against collusion attacks:In the proposed scheme,each user possesses a unique global identity,Gid,which binds the search token components of a user together in a consistent manner.If some user wants to collude with another user then the binding fails and thus prevents two users with differentGidto collude [20].

Security against non-adaptive CKA:The following theorem guarantees the security against the non-adaptive CKA:

Theorem 1:The proposed scheme is secure against nonadaptive chosen keyword attack if the decisional parallel bilinear Diffie-Hellman exponent (DPBDHE) problem is hard.

Proof:We will start the proof by assuming that if there exists a probabilistic-polynomial time (PPT) adversary,A,who can break the proposed scheme,then we can construct another probabilistic-polynomial time adversary,C,who can break DPBDHE assumption,given an instance (D,V) of the DPBDHE problem.C simulates the challenger in the security game defined for the proposed scheme as follows:

Global Setup Phase:Given the DPBDHE problem instance(D,U),Cpublishes global public parameters,GPP=(e,p,g,G,GT).

Initialization Phase:A selects a set of corrupted consensus nodes,CNc⊆CN:|CNc|≤k−1,and constructs the challenge LSSS matrix,A′,of sizel∗×m∗using the challenge access structure,A∗.Letc=|CNc|.

wherem′≤qandXare the set of attributes in the challenge access structure.

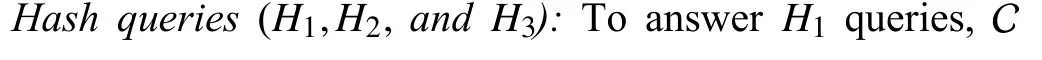
Ifx∉ρ∗(l∗),then C knows αi,βiand generates the secret ke y as in the originalscheme.Ifx∈ρ∗(l∗)andSi∩ρ∗(l∗)=∅,which implies that the attribute is in the challenge access structure,but none of the attributes of useriis present in it,then C uses the output ofH1andH2oracles and sets

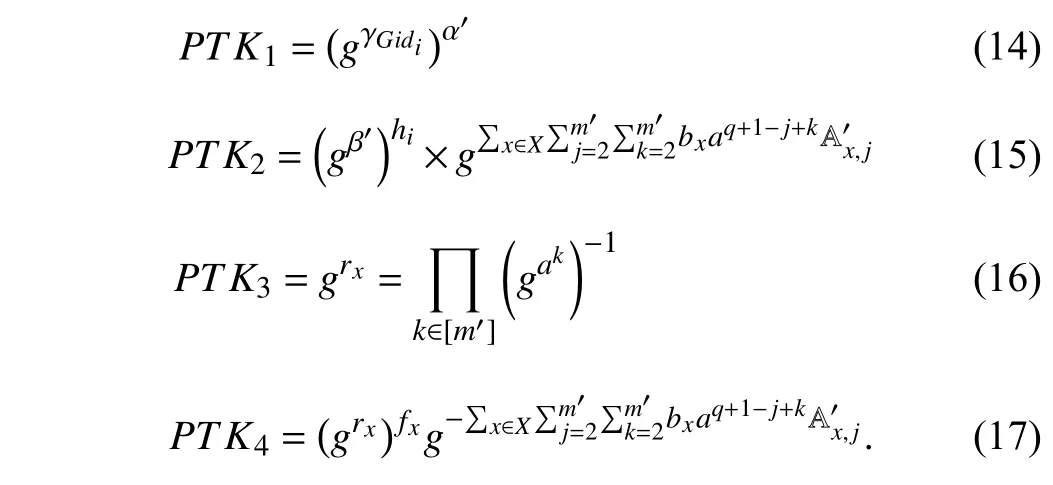
Otherwise,x∈ρ∗(l∗) andSi∩ρ∗(l∗)≠∅,which means the user has some shares of the challenge access policy.Then for each suchx∈X,Cuses another output ofH1andH2oracles and sets

The partial search token is then used by C to answer the search token queries for any keyword.

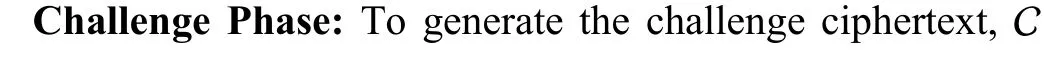
Output Phase:If the guess of the adversary is correct,i.e.,b′=b,then C correctly outputs the challenge termV=e(g,g)saq+1,otherwise C outputsa random elementofGT.

C.Performance Analysis

In this section,we will first present the analysis of the proposed scheme comparatively with exiting schemes in the literature and then provide the implementation details of the proposed scheme to validate the theoretical claims.

1) Comparative Analysis

The comparative analysis of the proposed scheme is done in terms of the features,the storage cost,and the computational cost with the similar CP-ABE based searchable encryption schemes in the literature.The notation used throughout the comparative analysis is given in Table I.

Table II compares the basic features of the proposed scheme with related schemes.

2) Asymptotic Complexity Analysis

In this section,we will compare the storage and the computational cost of the existing CP-ABE based similar searchable encryption schemes in the literature with the proposed scheme,as shown below in Table III.Here,we will not compare every CP-ABE based searchable encryption scheme,but we will focus only those CP-ABE based searchable encryption schemes which have multi-authority support to manage a diverse set of users.The storage cost is computed in terms of the number and size of the group elements involved.In contrast,the computational cost is computed in terms of the number and types of operations involved in the output of each algorithm.

As shown in Table III,the storage and computational cost of the key generation algorithm is constant in the proposed scheme,unlike other similar schemes where it varies with the number of attributes.Therefore,the proposed scheme reducesthe burden from attribute authorities to manage the secret key of users.Instead,it is managed by the consensus nodes,and that too is done only when the consensus nodes receive a search token generation request from the end-users.For remaining algorithms,storage and computational cost is dependent upon the number of attributes.However,the proposed scheme is genuinely decentralized and more secure due to the application of blockchain technology.Further,the search token needs not be stored by the user; it can be computed on-demand with consensus nodes.Consensus nodes generate a partial search token,upon which the user will perform some exponent and multiplication operations(minimal cost operations) to compute the complete search token.Therefore,we can say that the cumbersome process of computing search tokens corresponding to the user’s attributes is delegated to the blockchain.Furthermore,system initialization is also managed by the consensus nodes in the blockchain.Therefore,the proposed scheme is genuinely decentralized and is free from a single point of failures.

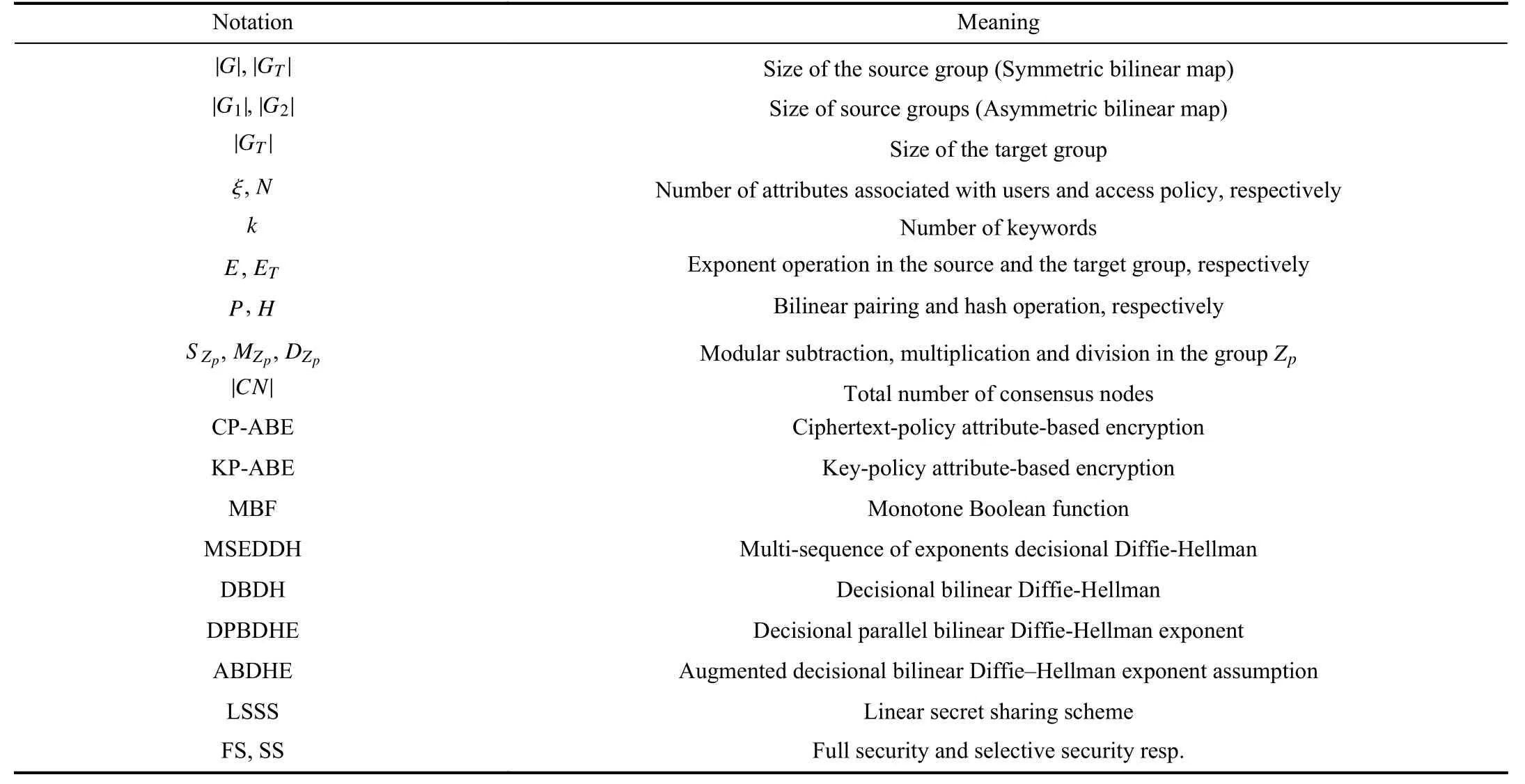
TABLE INOTATION AND DESCRIPTION

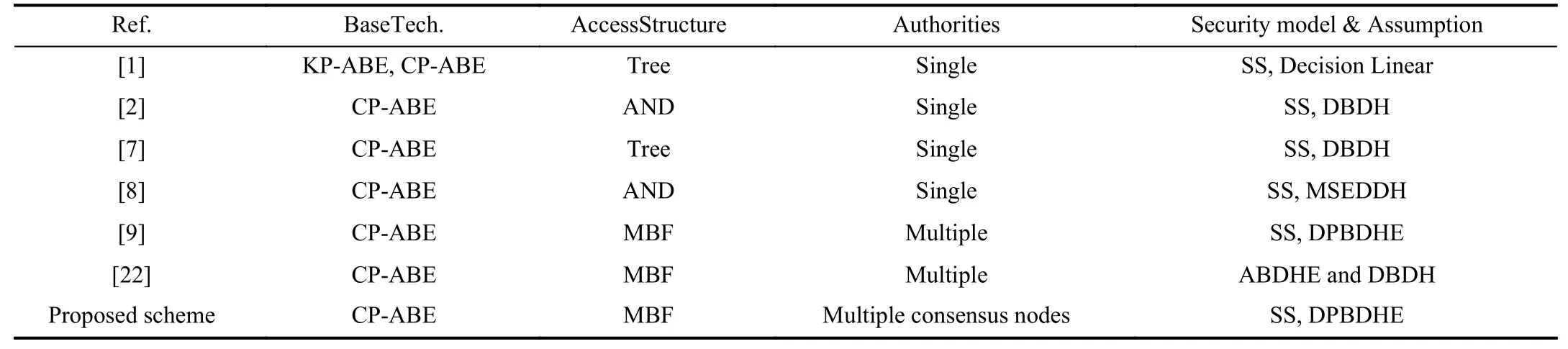
TABLE IICOMPARISON OF BASIC FEATURES OF THE PROPOSED DECENTRALIZED SEARCHABLE ENCRYPTION SCHEME WITH EXISTING SCHEMES

3) Experimental Analysis

Experimental setup:To evaluate the performance of the proposed scheme,the implementation is done on a 64-bit Windows 10 system with an Intel Core i3 processor 2.00 GHz and 4 GB RAM,in JAVA using the Netbeans-8.1 IDE and java pairing-based cryptography library (JPBC) [23].To create the symmetric bilinear map,we used a Type A pairing constructed on the elliptic curve,y2=x3+xover a fieldFq,whereq=3mod4 is a prime.In(this)pairing bothG1andG2are the group of points fromand hence it is called a symmetric pairing.

Parameter setting:The size of the base field is set to be 512-bit which offers a security equivalent to 1024-bit DLOG[23]and the order,pof source groupGand target groupGTis set to be 160-bit.The efficiency of the proposed scheme relies on the operations performed by the consensus nodes in the blockchain network and the remaining operations by the end users and the cloud server.The performance of the blockchain operations depends entirely upon the consensus mechanismand the computational power of the consensus nodes,which is not the focus of this paper.In this paper,we mainly focus on the regular operations performed by the end users and how blockchain technology assisted in reducing burden from these end users and the cloud,and compared that with existing multi-authority searchable encryption schemes [9],[22].

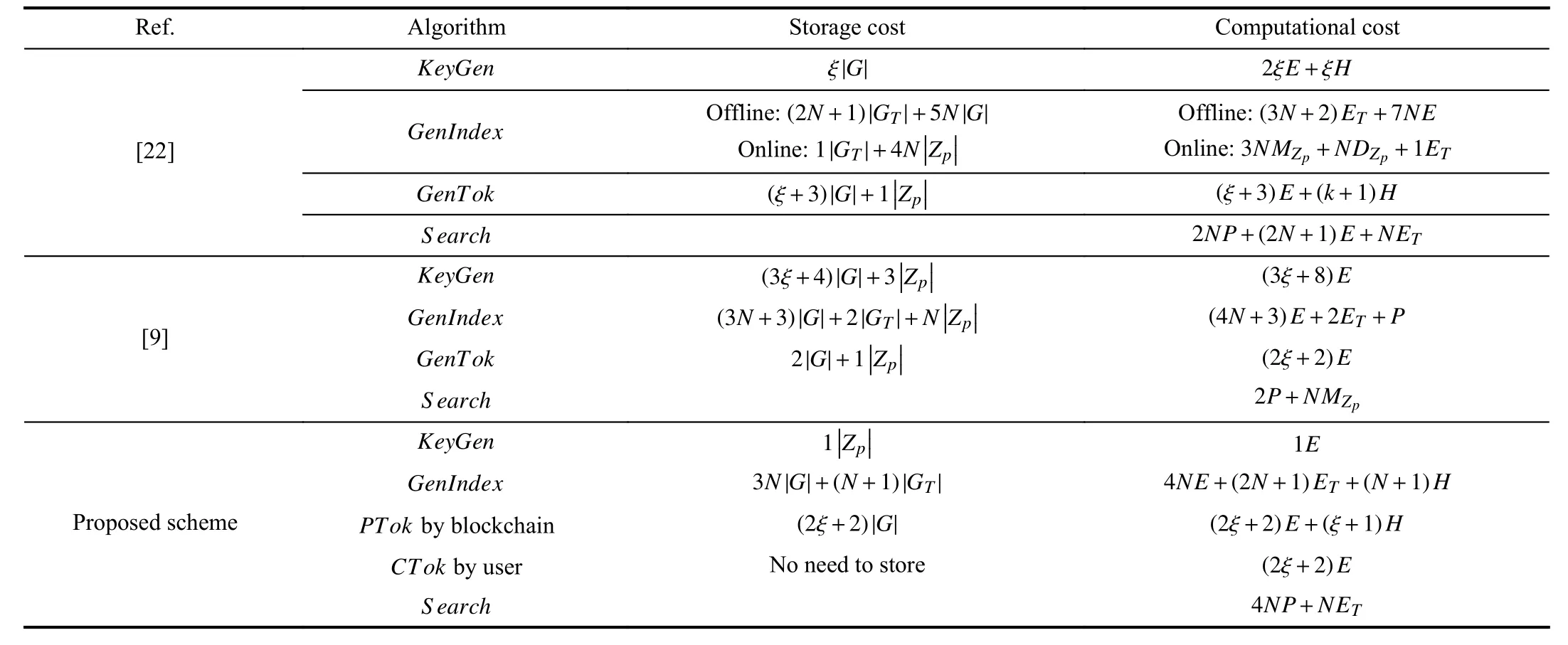
TABLE IIICOMPARISON OF STORAGE AND COMPUTATIONAL COST OF THE PROPOSED DECENTRALIZED SEARCHABLE ENCRYPTION SCHEME WITH EXISTING SCHEMES

TABLE IVAVERAGE EXECUTION TIME (AAETTT) R(SIBEUCTOEN DU)N OIFV ETRHSEE ,A ALCGCOERSIST HPOMLSI COYF TAHNED PTRHOEP SOESTE D ξ SISC KHEEMPTE TWHEH ESRAEM TEH E NUMBER OF ATTRIBUTES IN

Procedure:To demonstrate performance,we have varied the number of attributes in the attribute universe,and the access policy in the set ξ from 10 to 50 with a step length of 10.In each step,the experiment has been executed 20 times to find the average time taken by each algorithm which is listed below in Table IV.

For the better demonstration of the results,we plotted the time complexity of each algorithm against the number of attributes comparatively,as shown in Fig.5.As mentioned in the asymptotic complexity analysis section,we will compare the time complexity of the proposed scheme with existing similar decentralized CP-ABE based searchable encryption schemes.

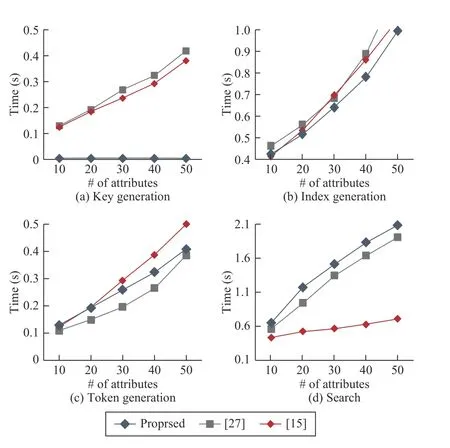
Fig.5.Average execution time taken by (a) KeyGen,(b) GenIndex,(c)CTok,and (d) Searchalgorithms.

Fig.5(a) denotes the time taken by the key generation algorithm of the proposed scheme and other related schemes[9],[22].The key generation time for the proposed scheme is constant and does not vary with the number of attributes,while in [9]and [22]a linear graph can be observed.In the proposed scheme,the attributes are not embedded while generating the secret key for the user.At the same time,it is done directly during the search token generation by the consensus nodes.Here,the user will generate a public and private key pair for himself/herself corresponding to his/her unique global identity and sends the public key to blockchain network to register himself/herself to the blockchain network.Therefore,the proposed scheme eliminates the need of a central authority for the management of users attributes.It is done by the consensus nodes when a search token generation request is received from the user.

Fig.5(b) shows the time taken by the index generation algorithm.As it can be observed from the Fig.5(b),the index generation time of the schemes under consideration is almost the same and varies linearly with the number of attributes.Fig.5(c) presents the time taken by the search token generation algorithm at the user’s end.It also increases linearly with the number of attributes for all the three schemes.Fig.5(d) shows the time taken by the search algorithm executed by the cloud server.It also varies linearly with the number of attributes,and the proposed scheme has higher time complexity as compared to [9]and [22].The time complexity of [9]is least among the three since it only has two pairing operations,and thus the time taken by the search algorithm is almost constant.However,this algorithm is executed by the cloud server,which is assumed to have plenty of resources,and will not affect the performance of the scheme.Hence,the experimental results validate the theoretical claims made in the asymptotic complexity analysis section.

VI.CONCLUSION AND FUTURE DIRECTIONS

In this paper,we have proposed a truly decentralized,robust and computationally efficient ABSE scheme for healthcare CCPS with the assistance of consortium blockchain.The devices involved in a typical healthcare CCPS are resource constrained.Further,the users in a healthcare CCPS may belong from a variety of domains,and to manage such a large number of diverse users,a single authority is not sufficient.

Keeping that in mind,we have proposed a scheme where computationally intensive tasks are delegated to the consensus nodes in the blockchain network to increase efficiency and to avoid single point failure.The consensus nodes are responsible for initializing the system and generating partial search tokens for users.This helps in reducing the computational burden from data users and also eliminates the need for a global central authority which sets up the system.Further,consensus nodes in the blockchain network handle the user’s attributes,unlike the central trusted authority in similar ABSE schemes.Therefore,a large number of attributes from diverse domains can efficiently be handled by the proposed scheme.The proposed scheme addresses both of the aforementioned constraints in a healthcare CCPS,and thus works well in this scenario.

As a part of future work,one can work in two directions.First,one can impart efforts to incorporate a proper reward mechanism like the bitcoin network.In the proposed scheme,if we add a proper mechanism to reward users financially by means of a token,which can be spent by the users either in availing healthcare services or can be converted to other cryptocurrencies in return for sharing their data with government and healthcare agencies.By doing this,we can inspire users to utilize the system for the benefit of both the healthcare agencies and themselves.Second,one can work on adding scheme-specific features like verifiability of the search results and handle the event of user revocation with the assistance of the blockchain network to increase the correctness,robustness and dynamicity of the system.