基于优化支持向量机方法的风电场风速预测研究

罗默涵

摘 要：随着全社会用电量的逐步增大以及国家双碳战略的逐渐落地，可再生能源的高效利用成为当前发展阶段需要不断探索的问题。由于存在无序性，风力发电难以大规模接入电网系统，若能有效预测风电场的出力并进行统一调度，将大幅提高风力发电利用率。基于此，首先阐述了支持向量机理论，然后针对其解决大样本问题的低效性进行了优化，最后通过实验对比了优化的支持向量机方法在风速预测中的有效性和准确性。

关键词：风电场;风速预测;支持向量机

0    引言

风力发电作为波动性能源，大量接入电网时需要接受电网的统一调度，而对能源进行调度的前提是能掌握发电机的变化趋势，当前的预测技术基本基于相似日数据以及天气数据进行分析，并制订相关调度计划[1-2]。

难以直接对风力发电进行预测的原因在于风速变化的无序性，这直接导致了风机转速的不稳定以及发电功率的无序变化，所以目前电网难以接受大量风力发电的并网运行[3]。因此，对风力发电进行更为准确的预测，是支持风力发电大规模并网的关键所在[4]。而究其根源，需要对风速进行有效预测，本文针对此问题进行了相关研究。

1    支持向量机基本理论

支持向量机（Support Vector Machine，SVM）是在20世纪90年代初提出的，它建立在统计学习理论的VC维概念和结构风险最小原理基础上，可以根据有限的样本信息实现计算量和计算能力之间的平衡性，是归属于统计学的新兴分支[5]。其独特的对于数据的归类识别能力，使其能够有效地应用到机器学习的相关领域进行预测分析。

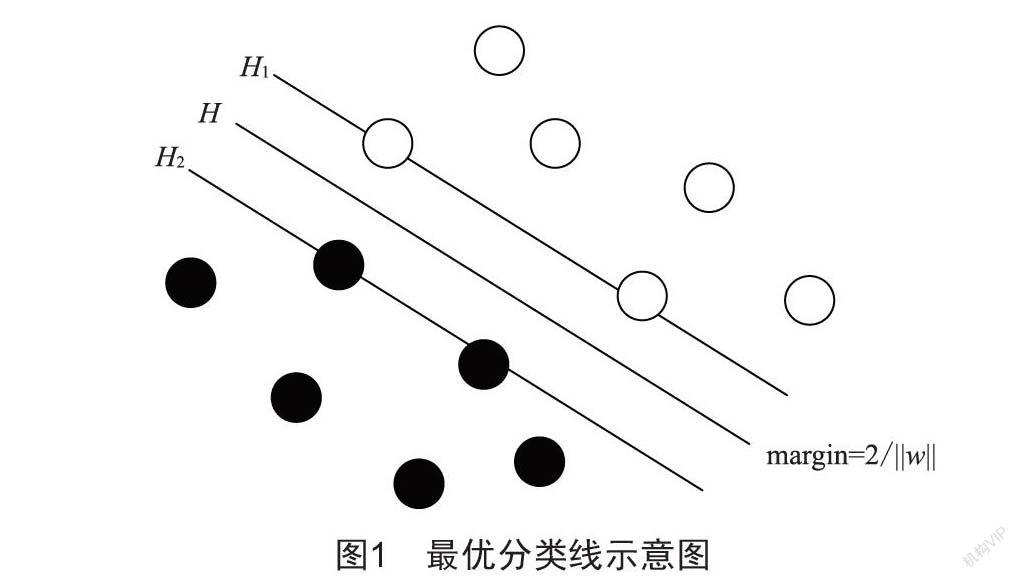
对于群体在线性可分情况下的分类情况示意如图1所示，由图可知，两类不同的样本被分类线H分离，且存在两条与H平行的直线H1和H2分别经过了两组样本最靠近分类线的样本。针对此结果，可得出最优分类线的定义：针对两样本存在一条分类线能将其正确分类，而且H1和H2的距离最大。

针对以上基本理论，将分类线H的方程设为wx+b=0，并将该方程归一化，有：

yi（w·xi+b）-1≥0                  （1）

在方程（1）的樣本集（xi，yi）中有以下关系：xi∈Rd，yi={-1，+1}，i=1，2，…，n。据此可知分类间隔（margin）为2/||w||。若要在计算中实现分类间隔最大化，则通过约束实现||w||2最小即可。

据此，最优分类线在数学上的定义可描述为满足式（1）且使||w||2最小的方程表达式，而在H1和H2上进行训练的样本点则为对应的支持向量。

以上分析是基于二维平面概念而言的，那么在VC维空间里，则所分析的样本理论上分布在一个超球范围内，同样存在一超平面能够将超球内的样本进行有效分类，将超平面表示为f（x，w，b）=sgn（wx+b）。若要实现有效分类，则该函数满足以下关系：

h≤min（A2R2，N）+1                       （2）

其中，R和N分别为超球半径和空间的维数，且在超球中存在条件||w||≤A。与二维系统同理，当w最小时，VC维可取得最小值。

为了实现对最优分类面的求解，通常引用拉格朗日优化方法，利用该方法将此问题转化为对偶问题，可得：

Q（α）=αi-αiαjyiyj（xi·xj）          （3）

式（3）中的αi对应于每个数据样本中的拉格朗日乘子，且该因子有以下关系：

αiyi=0，αi≥0，i=1，2，…，n    （4）

由于式（3）受到不等式的约束，所以能够求解出该方程的唯一解。同时，对于系列解的结果中存在少部分αi不为零的数据样本的合集便组成了支持向量。基于以上解的结果，可知分类曲面所对应的最优函数表达式为：

f（x）=sgn（w·x+b）=sgn

αi*yi（xi·x）+b*         （5）

据前文分析可知，大部分的求解结果αi均为零，所以式（5）中的有效求和只是有效支持向量的解的和。对应的分类阈值b*可通过将式（5）代入任一支持向量求得。

2    优化的支持向量机算法研究