基于点云数据的电力线弧垂验收校核及应用研究
2021-11-06徐梁刚时磊王时春余江顺龙新
徐梁刚 时磊 王时春 余江顺 龙新


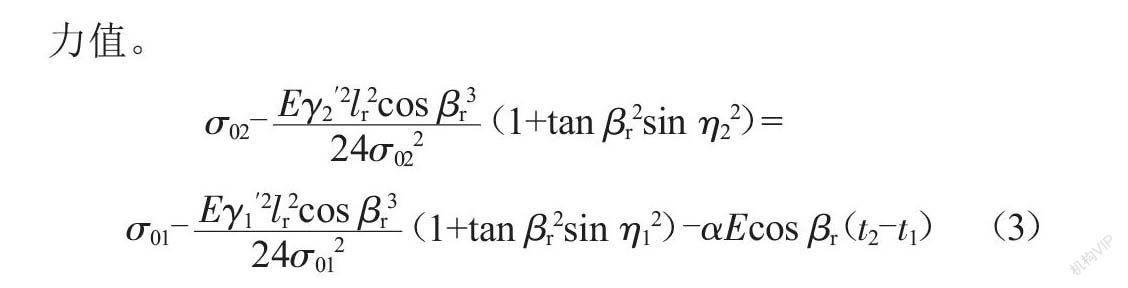
摘 要:从电线力学理论出发,提出一种基于点云数据的电力线弧垂验收校核方法。通过计算电力线比载,判断电力线控制条件,进而求解电力线控制应力,实现电力线任意工况应力的计算,并结合电力线弧垂公式建立电力线任意位置弧垂计算模型,最后通过与提取的电力线点云弧垂进行比对,完成电力线弧垂校核。
关键词:电力线;弧垂;比载;施工验收
0 引言
随着社会经济的发展,输电线路的新建与迁改呈现逐年增多的趋势。因而,作为电网建设生命周期中的关键一环,做好施工验收阶段工作对架空输电线路安全稳定运行起着重要作用[1-2]。为了保证架空输电线路建成后的安全运行,减少杆塔所受的不平衡张力以及满足导地线与交叉跨越物之间的安全距离,必须对架空输电线路的弧垂进行严格控制[3]。当前对于架空输电线路弧垂的观测校核方法有等长法与角度法[4],这两种方法的操作均较为复杂,且对人员技能要求较高。随着无人机以及激光LiDAR技术的推广应用,通过分析机载LiDAR点云数据,进行弧垂验收校核成为可能[5-7]。
1 电力线控制应力计算
电力线弧垂最低点水平应力是决定弧垂大小的主要因素,随着气象条件变化,其值也在变化,必定存在一种气象条件,使该应力最大,这一气象条件称为电力线控制条件,对应的应力称为电力线控制应力[8]。一般情况下电力线可能的控制条件有低温、大风、覆冰、高温、年平等,究竟哪种气象条件为电力线的控制条件,取决于档距大小。根据导线许用应力定义,前4个工况下的导线许用应力均为σm,年平工况条件下导线的许用应力为σp,则有:
导线许用应力:
σm== (1)
年平均使用应力:
σp= (2)
式中:K0为年平系数,取值通常为0或1;Tb为计算拉断力(N);K为安全系数,取值不小于2.5;A为导线截面积(mm2);Kp为年平均系数,取值不小于4。
1.1 比载计算
作用在电力线上的分布荷载包括自重、冰重、风荷载等。根据作用方向的不同可分为垂直比载、水平比载、综合比载,其计算公式如表1所示。
1.2 控制应力计算
求解控制应力之前,首先得判断线路的控制条件。控制条件判别方法有图解法、列表法以及试推比较法,由于图解法与列表法在进行编码计算时编码过程较为复杂,且当前普通计算机计算能力较之以前也有大幅度提升,因而本文采用试推比较法进行电力线控制应力的判别。试推比较法基本理论可表述如下:
首先假设其中某个条件为有效控制条件,利用状态方程式(3)推求其他可能控制條件下的应力值。若均不超过各自的应力许用值,则假设正确;若其中某个条件下的应力超出其限度值,则应以该条件作为有效控制条件;若有多个条件的应力超限,则以超限最多的条件作为假定控制条件,重新进行计算。通过上述步骤即可判断出线路控制条件及其对应的控制应力。在求得控制应力之后,通过状态方程式(3)即可求解出其他任意工况条件下电力线的应力值。
σ02-(1+tan βr2sin η22)=
σ01-(1+tan βr2sin η12)-αEcos βr(t2-t1) (3)
式中:σ02、σ01分别为两种状态下架空线弧垂最低点处应力;α、E分别为架空线的温度膨胀系数和弹性系数;γ2′2、γ1′2分别为两种状态下架空线综合比载;lr为连续档耐张段的代表档距;βr为高差角;t1、t2分别为两种状态下架空线的温度;η1、η2分别为两种状态下架空线风偏角。
2 悬链线方程与弧垂计算
2.1 悬链线方程
原始的电力线悬链线方程及其导出的有关公式中都涉及双曲函数,计算较为复杂。工程计算中常使用简化公式,其中精度较高且广泛应用的为斜抛物线法[8],根据斜抛物线法,选取线路方向为坐标系x轴,平行于比载方向为y轴,则简化后的悬链线方程表达式如下:
y=xtan β- (4)
式中:β为电力线高差角;γ为电力线比载;l为电力线档距;σ0为电力线弧垂最低点水平应力。
结合式(4),根据弧垂定义,则可得到电力线任意一点的弧垂为:
fx= (5)
对式(5)关于x求导,并令x=0,则可知最大弧垂发生在档距中央及x=l/2处,且最大弧垂表达式为:
fm= (6)
2.2 电力线弧垂计算
在自然环境中电力线一方面受到自重、冰重产生的垂直比载作用,另一方面还经常受到横向风荷载的作用。在二者的综合作用下,原来位于垂直平面内的架空线向风压方向偏摆。因而,在实际工程应用中,经常将电力线弧垂分别投影到垂直平面及水平平面进行计算。
2.2.1 垂直投影面内电力线弧垂