焊缝宽度对对接接头疲劳强度的影响

刘振雄 ，徐 刚 ，曹文涛 ，马春伟

（上海工程技术大学 材料工程学院，上海 201620）

进入21世纪，我国高铁事业取得飞速发展. 在一些大型高铁设施的工业结构中，特别是以焊接形式存在的结构中，往往要考虑工业结构的强度，尤其疲劳引起的失效在工程中尤为突出，因此强度设计对于传统强度的控制能力大大增强. 高铁长期运行过程中，受到风、挤压、撞击等多种复杂载荷的作用，其工业结构易产生裂纹，最终导致结构失效而引起事故. 为减少事故发生，研究工作者致力于探索提高疲劳强度的方法. 疲劳的定义核心为：材料受到循环作用的力，局部产生裂纹，发生永久性失效，最后断裂的过程[1−2]. 疲劳会因应力集中产生，在循环载荷作用下裂纹扩展，从而导致疲劳破坏. 而对接接头处的几何形状突变会产生较大的应力集中，且常伴随各种焊接缺陷，是疲劳裂纹最容易萌发的区域. 焊缝宽度决定对接接头的强度[3−4]. 焊缝宽度增大可在一定程度上提高焊接接头的强度，但由于对接接头中存在焊接缺陷和夹渣等因素，焊缝容易产生应力集中.

目前，疲劳研究最常用方法是试验法，即通过大量试验收集相关的数据，整理成S−N曲线；另外一种方法是数值仿真. 传统的试验法耗资大、花费时间长. 而数值仿真法因减少了对大量试验的依赖及分析处理过程中的偶然误差，降低了研究成本，节省了时间，受到很多学者的青睐[5].

1 疲劳分析方法

目前，疲劳强度分析方法种类不多，主要有名义应力法、网格不敏感结构应力法和热点应力法，其对焊接接头的疲劳设计和分析帮助非常大[6].

1.1 名义应力法

名义应力是指在试样的有效横截面上计算得到的应力，是一种整体的等效应力，而不是实际作用于结构的局部力[7−8]. 对接接头的焊缝周围最容易出现该平均应力. 名义应力示意图如图1所示. 图中：F为构件所受的外载荷力；σn为焊缝部位的名义应力.

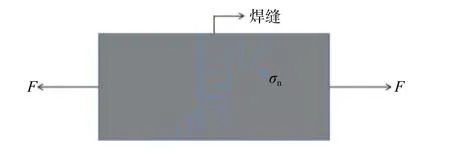
图1 名义应力示意图Fig. 1 Nominal stress diagram

获取名义应力的方法通常是通过贴应变片获得实测动应力数据或通过有限元方法计算获取.其中，贴片方法虽然精度较高，但测试比较繁琐，耗资较大，不推荐采用. 目前使用更多的是有限元法. 各种结构疲劳设计规范中，广泛使用基于名义应力的焊接构件疲劳评定方法，应力和应力集中系数在名义应力法中充当重要参数.

1.2 网格不敏感结构应力法

网格不敏感结构应力法是通过疲劳模拟软件计算节点力并且求解焊缝处的结构应力，解决了焊缝处应力求解出现较大误差的问题，能更好地探索影响焊缝处疲劳的影响因子.

网格不敏感结构应力法具有很多优点，其中比较显著的是完全克服了对于网格尺寸和单元类型等因素敏感的缺点，同时可以不再考虑热点应力法在分析典型对接接头的限制，在结构的理论疲劳强度评定和寿命预测方面比另外两种方法表现得更为精准.

在T型对接接头中，由于应力集中的影响，焊趾处承受的应力最大. 该应力是由平衡等效结构应力场和自平衡缺口应力场两种简单应力场组成，如图2所示. 断裂力学将其描述为一种远端驱动力场[9].

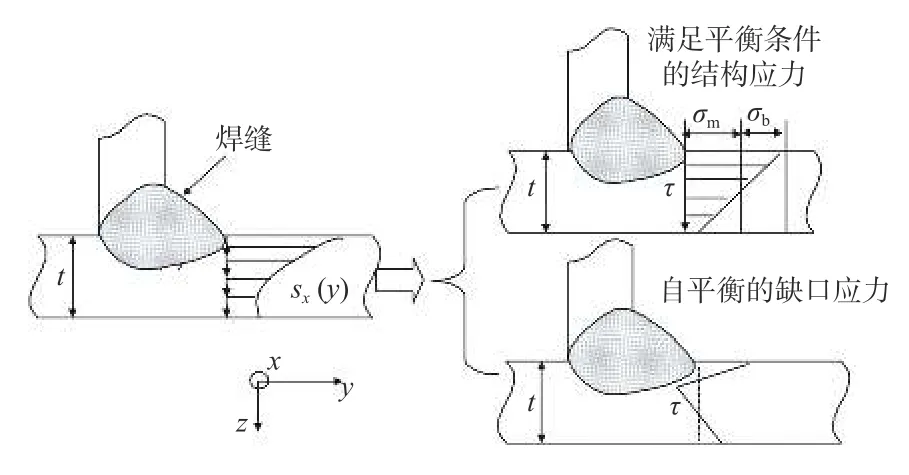
图2 基于厚度的结构应力Fig. 2 Structural stress based on thickness

在实体建模中，网格不敏感性需要平衡节点力和力矩. 通过有限元软件计算出节点力和力矩，可直接得到应力集中或重要位置的结构应力，保证对接接头网格尺寸达到理想的不敏感性. 结构应力的数学表达式可以描述为

式 中：σ为结构应力；σm为 膜应力；σb为弯曲应力.

1.3 热点应力法

对接接头焊趾处沿板厚方向的非线性应力分布如图3所示. 此处的应力称为缺口应力σloc，由 3部分组成，即膜应力σmem、 弯曲应力σbre及非线性峰值应力σnlp.热点应力由σmem和σbre两部分力组成. 计算热点应力前必须先定义垂直于焊趾一定距离的表面为热点区域，通过该区域内的应力值外推从而求得热点应力.

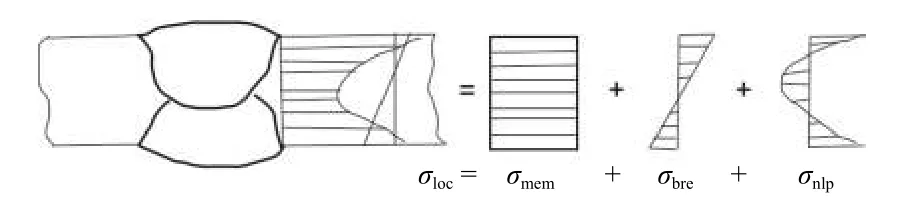
图3 焊趾处沿板厚方向的非线性应力分布Fig. 3 Nonlinear stress distribution at weld toe along plate thickness direction

2 对接接头有限元模型

2.1 有限元模型属性

本研究模型由Q235A钢板对接而成，焊缝模型简化为两块100 mm × 60 mm × 20 mm钢板对接焊接而成，三维坐标系已在模型中标出. 为操作方便和计算的精确度，所有模型都不开坡口，采用窄间隙气体保护焊. 按照焊缝模型几何尺寸，利用Pro/E软件建立焊缝宽度分别为1、10、20、25、30、50、70、90 mm的对接接头三维几何模型，其中焊缝宽度为1、25和90 mm的模型如图4所示.

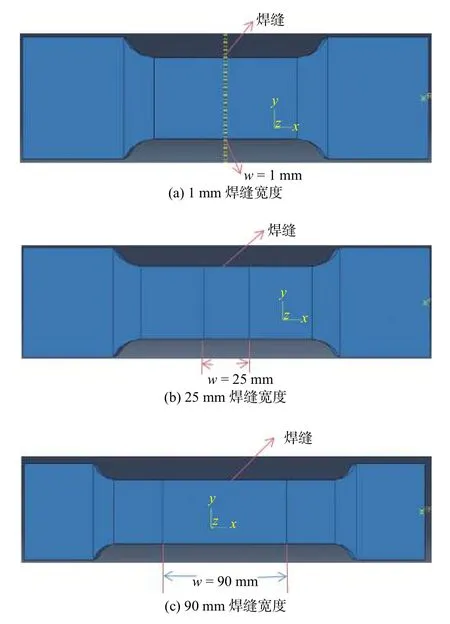
图4 对接接头三维几何模型Fig. 4 Three-dimensional geometric model of butt joints

钢板模型均采用左端面全约束，即UX = UY =UZ = URX = URY = URZ = 0，如图5（a）所示. 接头左端采用耦合约束，参考点选取右端面中心点，均按照拉伸载荷的方式进行定义，载荷类型为面载荷，如图5（b）所示.

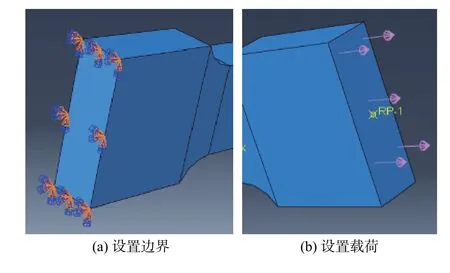
图5 对接接头载荷及约束定义Fig. 5 Definition of load and constraint for butt joints

2.2 有限元模型网格划分

利用ABAQUS软件自带网格划分功能对对接接头进行划分，有限元网格基本单元尺寸为0.5～6.0 mm，单元类型为八节点六面体三维实体单元（C3D8R），再对对接接头进行离散，其中焊缝宽度为1、25和90 mm对接接头的网格划分如图6所示.

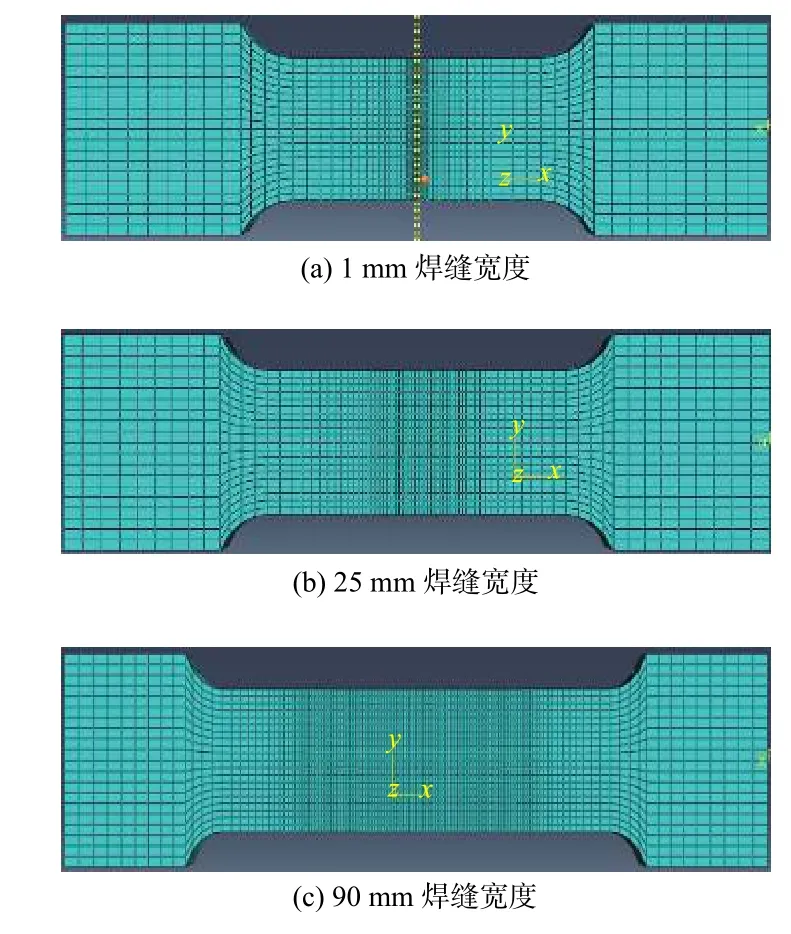
图6 对接接头的有限元网格Fig. 6 Finite element mesh of butt joint

3 有限元计算及结果分析

3.1 对接接头相关参数

将建好的有限元模型导入ABAQUS中，分别赋以焊缝和母材不同的材料，并正确定义边界条件及载荷，提交计算就可得到应力云图. 材料模型采用20 mm低碳钢板Q235A，焊缝材料采用高强度低合金钢焊条JM56，焊条直径都为1.2 mm，材料力学性能见表1. 材料化学组成成分见表2. 加载形式为拉伸载荷，面载荷为200 MPa，对接接头左端面设置全约束，进行应力强度计算.

表1 材料力学性能Table 1 Mechanical properties of materials

表2 材料化学组成成分Table 2 Chemical constituents of materials %

3.2 对接接头结构应力求解

要正确求解网格不敏感结构应力，需要使用ABAQUS软件准确定义焊接基本信息. 焊接区域单元、焊线、起始单元和起始节点等元素组成一条完整焊线，各元素定义如图7所示.

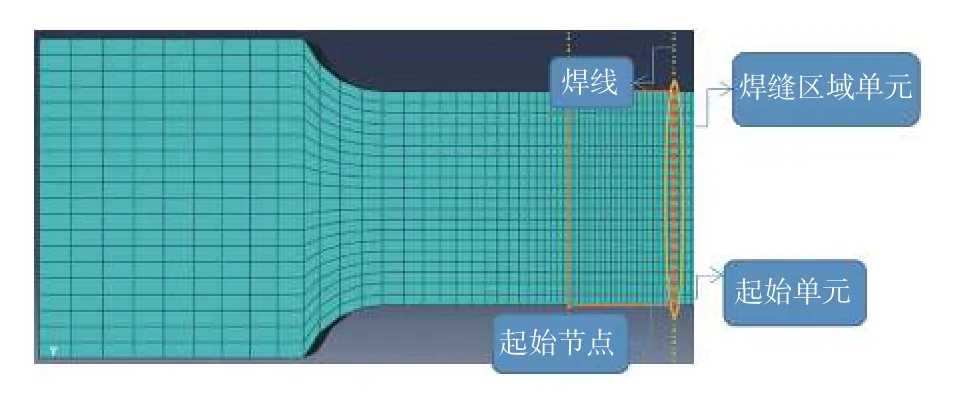
图7 有限元模型定义的相关参量Fig. 7 Related parameters defined by finite element model

焊缝对接接头的最大 Mises 应力云图如图8所示. 其中，“Avg：75%”表示当相对节点变量小于该值时，该节点的结果才被平均. 相对节点变量=（节点变量的最大值−节点变量的最小值）/（区域内的最大变量值−区域内的最小变量值）. 从应力云图可知，虽然焊缝宽度为1、25和90 mm时，3种焊接模型宽度变化较大，但应力整体分布规律相似. 有两处区域存在较大的应力集中：第1处为结构形状突变处，第2处为焊趾处. 分别选取应力集中区域和焊趾处应力集中最大的点为参考进行分析. 由图8（a）可见，由于焊缝宽度较小，应力几乎全部集中在整个焊缝处；由图8（b）可见，焊缝宽度为25 mm时，焊趾处即为最大应力位置，且相对于1、10、20 mm焊缝宽度时应力值变小；由图8（c）可见，相对于25、30、50、70 mm焊缝宽度，焊缝宽度 为90 mm时应力值略微增大.

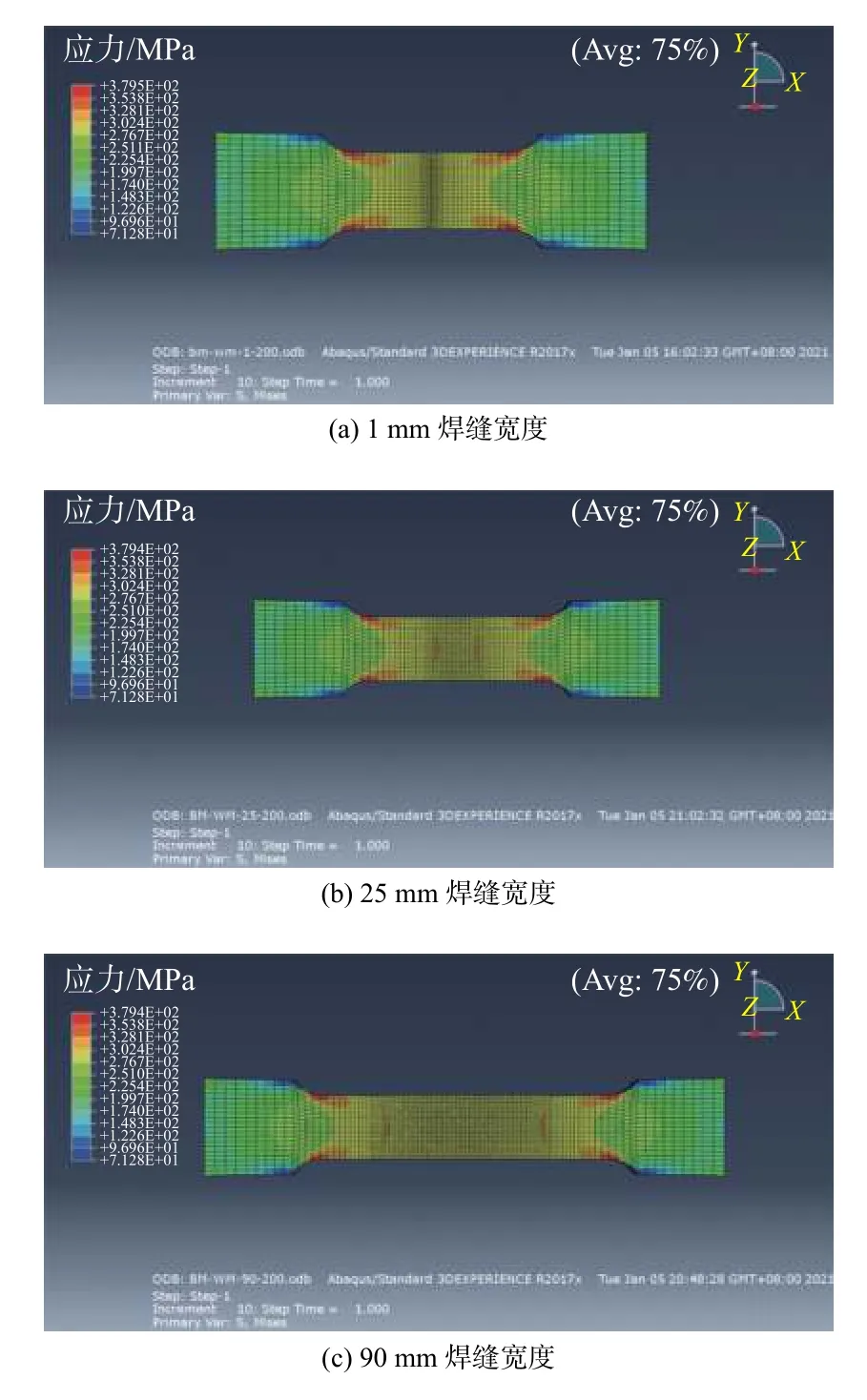
图8 对接接头Mises应力云图Fig. 8 Mises stress nephogram of butt joint

3.3 应力结果分析

由于对接接头出现应力集中现象，因此选择应力集中系数（Stress Concentration Factor，SCF）作为参数，即结构应力和名义应力之比. 对接接头在相同加载的情况下，各接头对应的应力集中系数见表3.

根据图8焊缝对接接头的应力云图可以发现，焊趾位置存在应力集中现象. 普遍认为，焊趾处的应力集中现象是由焊缝余高引起的，但本研究所建模型去除了焊缝余高，所以产生应力集中的原因是焊缝区材料和母材的静载强度不一样. 根据表1提供的力学性能，对接接头为高匹配. 随着焊缝宽度的改变，焊缝和母材的静载强度差异也在改变. 从表3数据分析发现，焊缝宽度在1～25 mm时，对接接头的应力集中系数逐渐变小，但是变化非常小. 有限元模型结构在焊缝处应力变小是因为随着焊缝宽度变大，所施加的载荷不变，单位面积平均受力减小. 焊缝宽度在25～90 mm时，其对应的应力集中系数开始变大.

表3 对接接头应力集中系数Table 3 Stress concentration factors of butt joints

4 对接接头疲劳性能分析

根据图8得到各焊缝宽度对对接接头的应力分布，对其疲劳寿命进行模拟. 首先将得到的结构应力结果.odb文件导入ABAQUS软件Fe-safe模型中，设置弹性模量、抗拉强度和疲劳参数后进行疲劳寿命计算.为减少工作量、加快计算效率，只对焊缝部位进行寿命计算. 焊缝宽度分别为1 、20 、25 和90 mm时疲劳寿命云图如图9所示. 寿命云图显示，焊缝最危险的区域在焊趾处，寿命与应力呈非线性反比关系，随着焊缝宽度变大，焊缝失效率变小，对接接头对应的疲劳寿命先变大再变小.

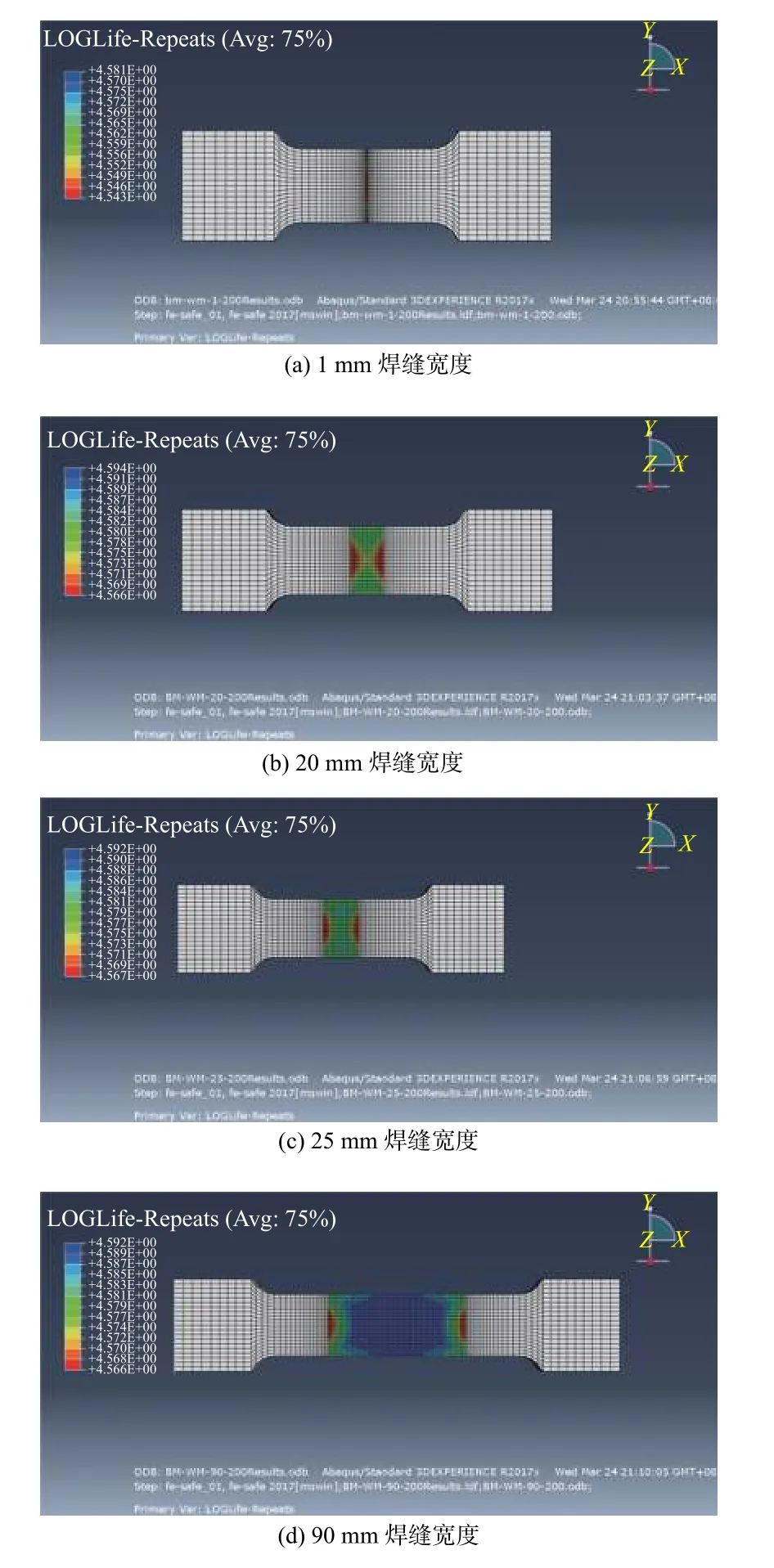
图9 对接接头疲劳寿命云图Fig. 9 Fatigue life nephogram of butt joint

为更加直观地表达焊缝宽度对对接接头疲劳性能的影响，可以分别对同种有限元对接接头模型施加不同的应力，再各自进行寿命计算. 根据国际焊接协会（IIW）标准中疲劳累积损伤理论，选择疲劳等级FAT=100疲劳强度S−N曲线，损伤比计算式为

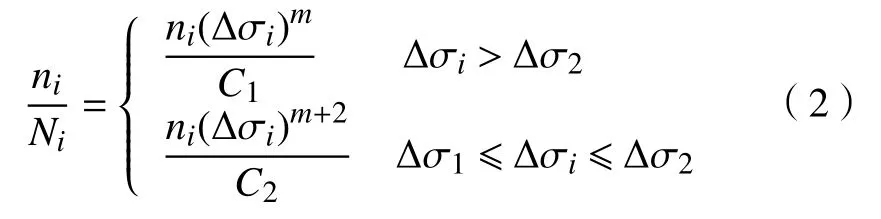
式中： ∆σ1为 常幅疲劳极限； ∆σ2为截止疲劳极限，分别为S−N曲线上的应力幅值； C1、C2为常数；m为S−N曲线的斜率； ni为载荷谱中应力范围为∆σi的循环次数； Ni为导致损坏的循环总数. 结合ABAQUS CAE软件准确定义焊接基本信息，焊接区域单元、焊线、起始单元和起始节点；通过三级加载的方式得到模拟应力，再通过Fe-safe有限元模型模拟计算得到疲劳寿命；将三级加载对应的循环次数代入式（2）计算得到损伤比，最终得到疲劳强度与性能见表4 .

对比表4中各种焊缝宽度的对接接头损伤比可以看出，对对接接头采用三级加载的方式，拉伸载荷依次为200、210、220 MPa，损伤比先随着焊缝宽度的增大而变小，之后随着焊缝宽度的增大而变大. 前期疲劳强度变大是因为焊缝宽度增大，焊缝的平均受力面积增大，降低了损伤比；后期疲劳强度变小是因为随着焊缝宽度的变大，焊缝的静载强度减小，从而使损伤比增大.

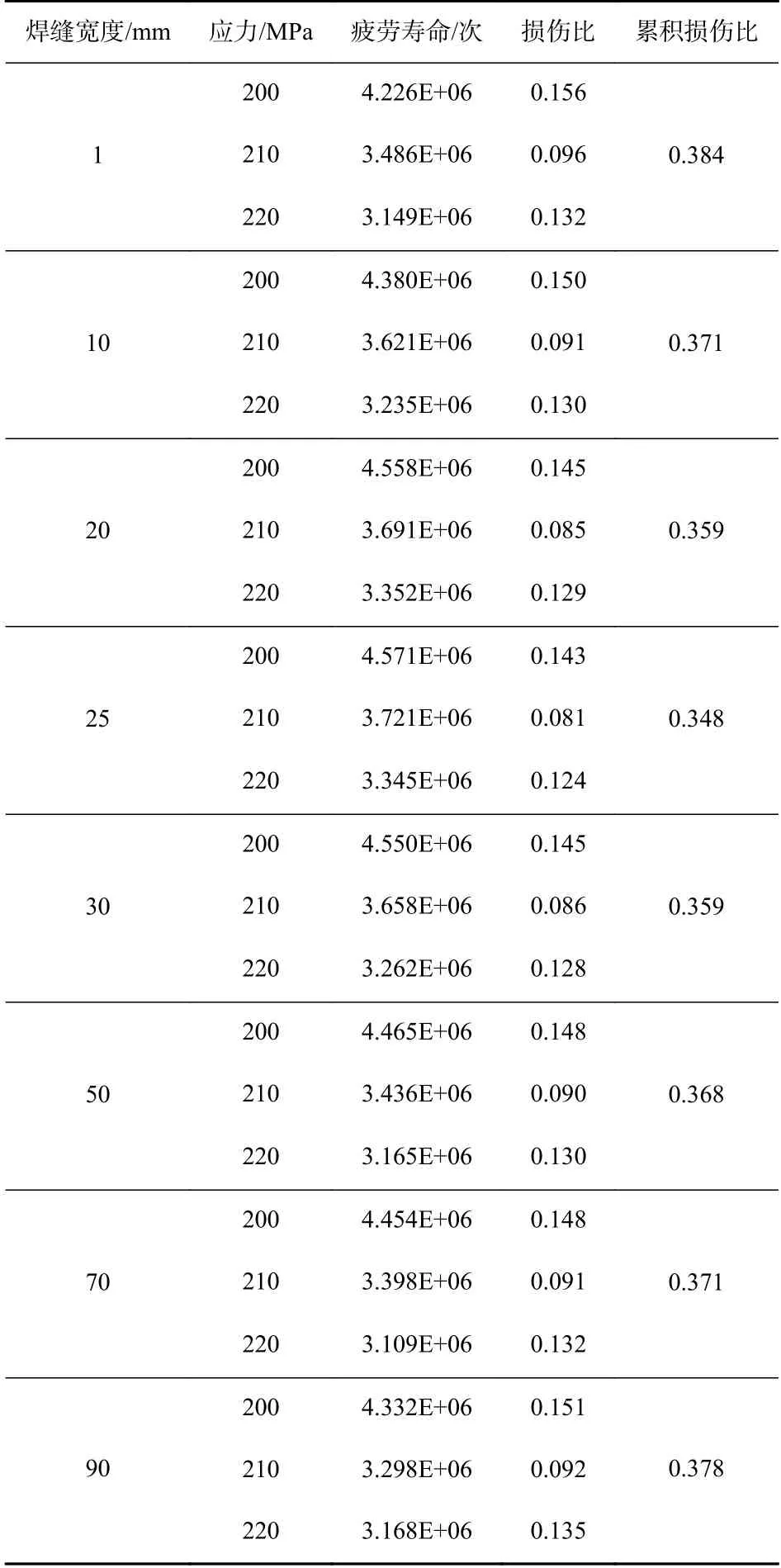
表4 疲劳强度与性能Table 4 Fatigue strength and performance

根据陈传尧[1]的研究，影响疲劳性能有若干因素：如平均应力因素，有可能是因为主应力或剪切应力的影响；载荷因素，有面载荷、压强等；尺寸效应和环境等因素. 而本文研究中焊缝宽度对疲劳性能的影响属于尺寸效应一类，尺寸因素改变了对接接头的拘束度. 焊缝宽度之所以对疲劳性能有影响是因为对接接头为高匹配对接接头. 在焊缝宽度增加的同时，由于焊缝和母材的静载强度不一样，构成高匹配对接接头，焊缝和焊趾处的结构应力差变大，因此，焊缝中应力集中程度不同[10−11].

根据赵峰[12]研究证明，结构应力较名义应力能够更好地表征材料几何尺寸对对接接头疲劳性能的影响，这也说明本研究所选方法是正确的；另一方面，其证明在应力比相同的情况下，板厚越小，疲劳性能越好，这也符合本研究中焊缝宽度大于25 mm的对接接头疲劳强度变化规律，即焊缝宽度越大，疲劳寿命越差. 根据罗超等[13]研究证明，一定板厚范围内，钢板越厚，静载强度越大，从而造成钢板疲劳强度差异，这也符合本研究焊缝宽度小于25 mm的对接接头疲劳强度变化规律，即焊缝宽度越大，疲劳寿命越好.

对接接头疲劳强度影响因素复杂，后期将建立带有裂纹的对接接头模型以及对对接接头进行温度场分析，从而分别分析焊缝宽度对焊缝内部缺陷和残余应力产生的影响.

5 结 语

本研究利用ABAQUS软件建立Q235A焊接平板对接接头模型，不考虑焊缝余高且不开坡口，不但减少了影响焊缝疲劳性能的因素，还简化了计算和分析过程. 对比名义应力法、网格不敏感结构应力法和热点应力法，选择能够克服网格尺寸和单元类型引起的误差，且更加精准的网格不敏感结构应力法为主要计算方法. 应用Fe-safe模型模拟焊缝对接接头的疲劳寿命，采用应力集中系数和损伤比比较分析焊缝对接接头疲劳强度与性能，得出如下结论：

1）采用网格不敏感结构应力法对不同焊缝宽度的对接接头进行研究，通过焊缝损伤比能很好地评定焊缝的疲劳性能；

2）从疲劳模拟的结果可以发现，在一定范围内，随着焊缝宽度变大，焊缝疲劳强度增强，但超过该范围后，焊缝宽度再增大，疲劳强度将会逐渐减弱；

在工业应用中，弄清焊缝宽度和疲劳强度之间的关系有助于降低经济成本，并且能使某些机器在获得最高疲劳性能的情况下，处于最简结构状态. 本研究只得出焊缝宽度与焊缝疲劳性能之间的关系，未来工作将具体研究焊缝宽度是如何影响焊缝寿命的.