浅谈守恒定律在分析化学教学中的应用

薛庆旺，贾丽萍，贾文丽，王术皓，李爱峰

聊城大学化学化工学院，山东 聊城 252000

守恒存在于整个自然界的千变万化之中，一切化学反应都遵循守恒定律，在化学变化中有各种各样的守恒，如质量守恒、能量守恒、元素守恒、电子守恒、电荷守恒等[1]。在分析化学中也不例外，许多公式的推导过程要用到守恒定律。此外，在有关化学平衡和滴定分析的计算中，运用守恒定律只需要考虑反应体系中某些组分相互作用前后某些物理量或化学量的始态和终态，利用其中某种不变的量建立关系式，不必了解过多的中间过程，避免了繁杂的分析和多重化学反应，从而达到速解、巧解化学习题的目的[2]。笔者在长期的教学过程中发现这种“纵览全局，抓住守恒，不看中间，只看两头”的解题思路具有思路简单、关系明确、计算快捷、不易出错等优点，更容易为学生所接受[3]。本文简要介绍守恒定律在分析化学教学中的应用。

1 公式的推导

1.1 质子平衡式的列出方法

在酸碱反应中酸失去质子，碱得到质子，因此，酸碱反应的实质是质子的转移，在酸碱转移质子的过程中，酸失去质子的总数与碱得到质子的总数必然相等，即质子是守恒的。在酸碱溶液中，有些物质(即酸)失去质子，有些物质(即碱)得到质子，因此，得质子产物与失质子产物的浓度之间存在一定的关系。根据质子守恒，可以列出质子平衡式(proton balance equation，PBE)。

PBE的书写有两种方法：推导法和直接列出法。前者是在物料平衡式(material balance equation，MBE)及电荷平衡式(charge balance equation，CBE)的基础上推导得出。下面以cmol∙L−1Na2CO3溶液为例，说明PBE的推导过程。

首先列出2个MBE：

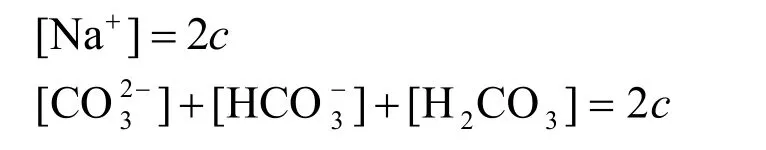
再列出CBE：

将2个MBE代入CBE：

整理可得PBE：

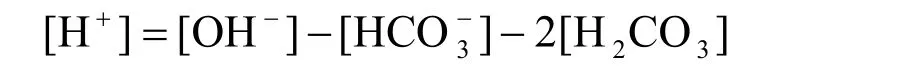
如图1所示，以Na2CO3溶液为例，说明直接列出法的步骤。

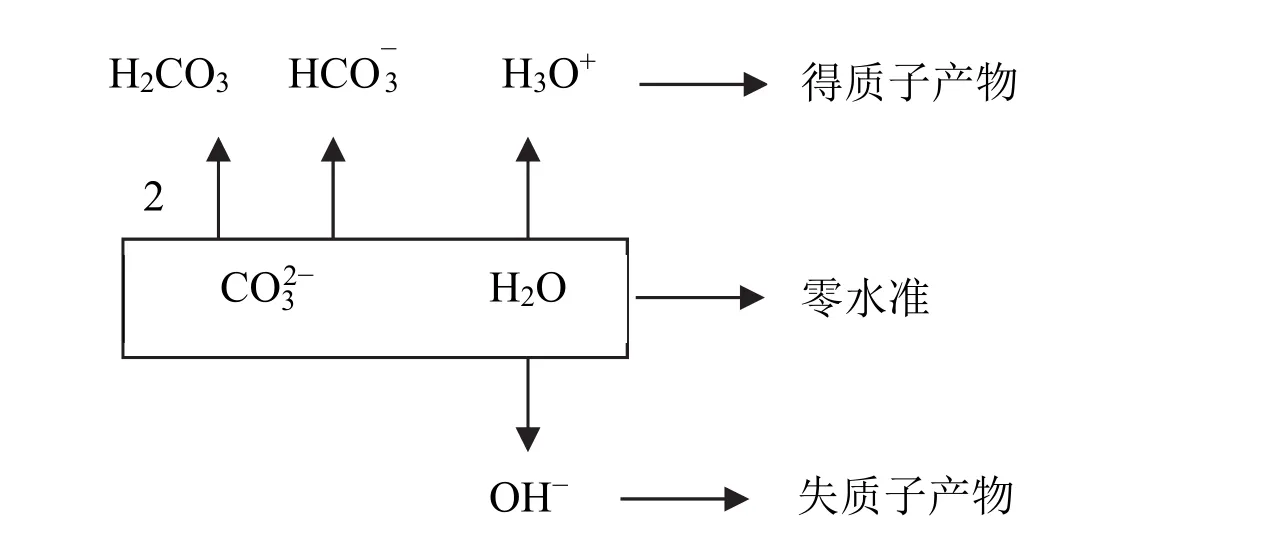
图1 Na2CO3溶液PBE的列出方法

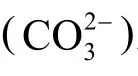
1.2 分布分数的计算公式

溶液中某酸碱组分的平衡浓度占其总浓度的分数，称为分布分数，以δ表示。δ将酸碱型体的平衡浓度与酸碱的总浓度联系起来，能定量说明溶液中各种酸碱组分的分布情况。通常酸碱的总浓度已知，知道了δ，便可求得溶液中各种酸碱组分的平衡浓度，这在酸碱平衡的学习中是十分重要的。

在δ的推导过程中，也用到了物质守恒。下面，以一元弱酸HA为例，说明δ的推导过程：首先，列出平衡常数的表达式：

整理可得：

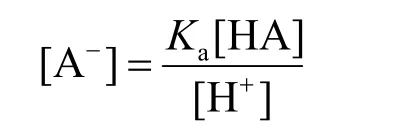
代入物料平衡式，可得：

将整理得到的物料平衡式代入酸型体δ的定义中，整理可得：

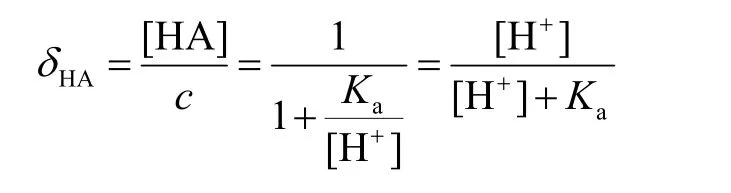
根据物质守恒，酸型体与碱型体的δ的加和等于1，可得碱型体的δ：

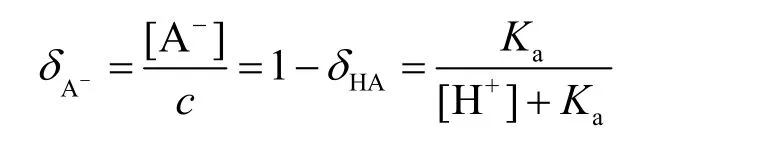
1.3 终点误差公式

在酸碱滴定中，由于酸碱指示剂的变色点与化学计量点不重合引起的误差称为滴定误差(titration error)或终点误差(ending point error)，用Et或TE表示。Et的推导也用到了MBE及CBE。

下面以浓度为c(mol∙L−1)的NaOH滴定浓度为c0(mol∙L−1)、体积为V0(mL)的HCl溶液为例，说明Et的推导过程：设滴定终点时，消耗NaOH溶液的体积为V(mL)。根据相对误差的定义，终点误差可以表示为：

因此Et的正负及大小取决于cV和c0V0的相对大小。列出2个MBE：

列出CBE：

将式(2)、(3)和(4)代入式(1)，整理可得：

由式(5)可知，Et的大小与滴定终点时HCl溶液的浓度成反比，浓度越大，误差越小。由于滴定终点时溶液的总体积与化学计量点时差距甚小，因此滴定终点时HCl溶液的浓度与化学计量点时近似相等，式(5)也可写作：

由上述推导过程可知，Et的计算公式是在定义式的基础上，引入MBE及CBE后逐步推导得出的。

1.4 化学需氧量的计算公式

化学需氧量又称COD (chemical oxygen demand)，是在水质分析中表征水体被微量有机物和无机可氧化物质污染程度的常用指标，它是将测定过程中消耗的氧化剂的量折合成氧气的质量浓度(mg∙L−1)来表示。如图2所示，以酸性高锰酸钾法测定COD为例分析测定步骤及计算公式的推导过程。

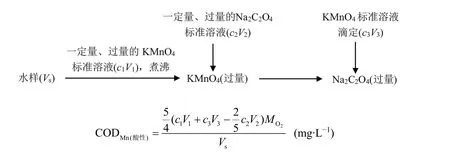
图2 酸性锰酸钾法测定COD的实验步骤及计算公式

根据上述测定步骤，可知：先后总共向水样中加入氧化剂KMnO4的物质的量为c1V1+c3V3，与其发生反应的还原剂有污染物和Na2C2O4。氧化剂的量是守恒的，即污染物消耗的KMnO4的物质的量与Na2C2O4消耗的KMnO4的物质的量之和等于KMnO4的总物质的量。Na2C2O4消耗的KMnO4的物质的量为2/5c2V2。因此，污染物消耗的KMnO4的物质的量为c1V1+c3V3− 2/5c2V2。由于在酸性高锰酸钾法中，1 mol KMnO4得5 mol电子还原为Mn2+。如果用O2做氧化剂，1 mol O2得4 mol电子还原为H2O。因此，1 mol KMnO4的氧化能力相当于5/4 mol O2，(c1V1+c3V3− 2/5c2V2) × 5/4就是污染物消耗的O2的物质的量。这样，COD的计算公式就不难理解了。

2 守恒定律在分析化学计算中的应用

利用守恒定律解决化学计算的问题是抓住物质变化过程中某一特定的量固定不变来列式求解，关键是抓住其中的守恒关系。在有关化学平衡和滴定分析的计算中经常会用到守恒定律，如元素守恒、电子守恒等，下面结合例题说明守恒定律的妙用。

2.1 元素守恒

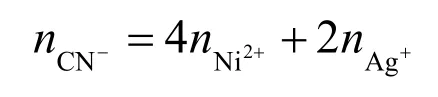
代入数据，可得：

2.2 电子守恒

例2[4]：移取乙二醇试液25.00 mL，加入0.04500 mol∙L−1KMnO4的碱性溶液50.00 mL，反应完全后，酸化溶液，加入0.3000 mol∙L−1Na2C2O4溶液10.00 mL，此时所有高价锰均还原至Mn2+，以0.04500 mol∙L−1KMnO4溶液滴定过量的Na2C2O4，终点时消耗2.30 mL，求试液中乙二醇的质量。(Mr(HOC2H4OH) = 62.05)

解法1：设25.00 mL乙二醇试液中含乙二醇xmmol。

乙二醇与KMnO4的反应：

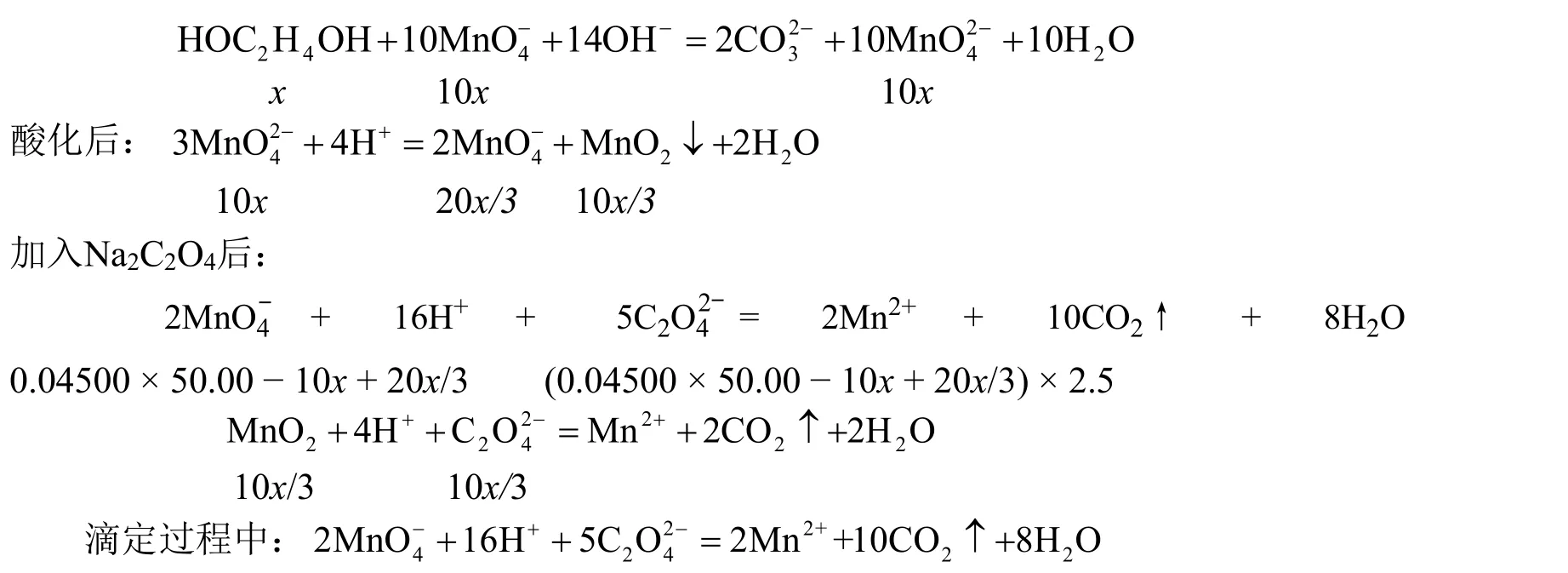
剩余Na2C2O4的量为：[0.3000 × 10.00 − (0.04500 × 50.00 − 10x+ 20x/3) × 2.5 − 10x/3] mmol

剩余的Na2C2O4刚好与2.30 mL 0.04500 mol∙L−1KMnO4溶液完全反应，

因此：0.3000 × 10.00 − (0.04500 × 50.00 − 10x+ 20x/3) × 2.5 − 10x/3 = 2.30 × 0.04500 × 2.5

解得：x= 0.5768 mmol

解法2：首先，根据参与氧化还原反应的物质的最终产物，分析得失电子的数目：

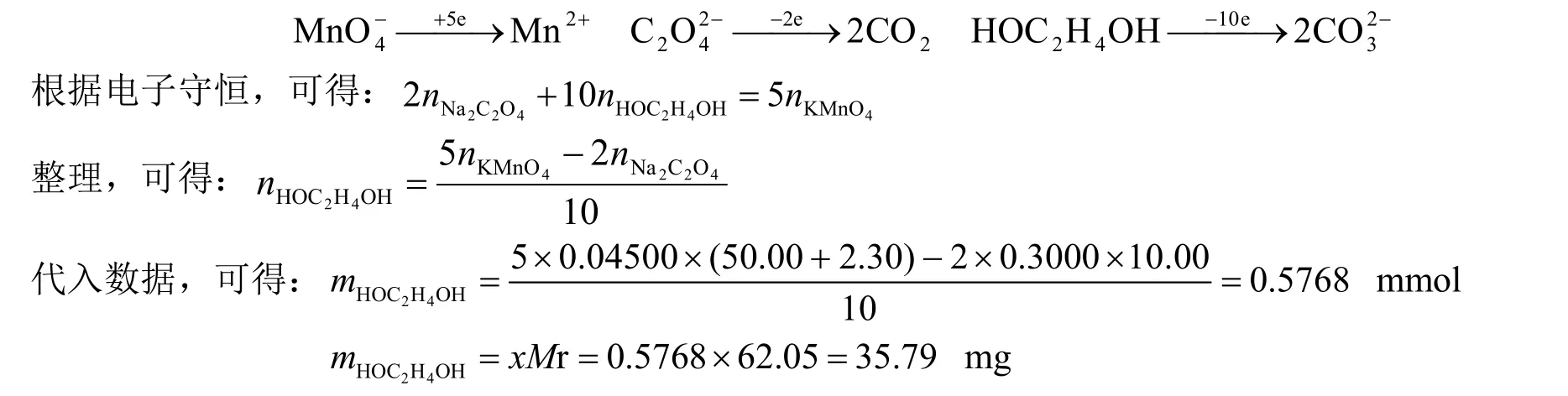
通过比较2种解法可以看出：解法1是将题目涉及到的每一个氧化还原反应进行剖析，搞清楚反应物及生成物的物质的量，步骤繁琐而且容易出错。解法2没有考虑中间的细节，而是搞清楚氧化剂及还原剂的始态和终态，分析得失电子的数目，根据电子守恒直接列出等量关系式，步骤简单、清晰易懂且不易出错。

2.3 元素守恒与电子守恒并用

解法1：设消耗的Ce4＋为x毫升

解得：x =26.67 mL

解法2：设消耗的Ce4＋为x毫升，固体I2刚刚出现沉淀时，溶液的总体积为V毫升(V= 50 +x)。首先，分析氧化剂与还原剂得失电子的数目：

根据电子守恒，可以列出：

将(7)、(8)式代入平衡常数的定义式，可得：

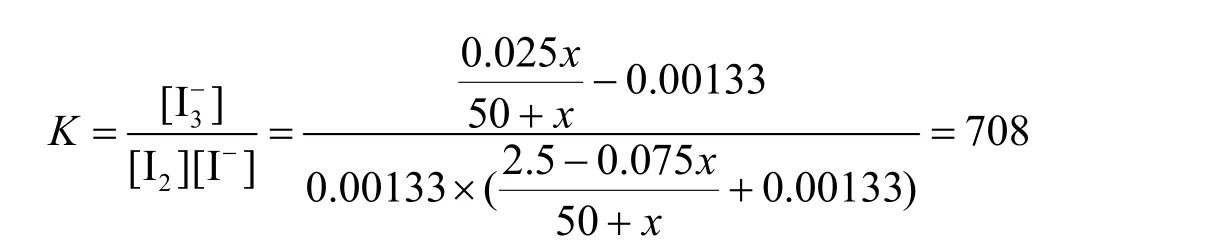
解得：x =26.67 mL

与例2相比，例3虽然涉及到的氧化还原反应的个数较少，但还涉及到络合平衡，因此情况变得更加复杂，只要抓住氧化还原反应中的电子守恒及络合平衡中的元素守恒，就能列出等量关系式，达到速解、巧解的目的。

3 结语

综上所述，在分析化学教学中，运用守恒定律推导公式可以帮助学生了解公式的来龙去脉，更好地利用公式解决问题；运用守恒定律解决复杂的计算问题，特别是氧化还原滴定的相关计算，不仅能够速解、巧解问题，更重要的是帮助学生从宏观全局的视角思考问题，形成科学的思维方式，从整体上把握问题的关键，从复杂的内容中理清头绪，将复杂的过程简单化，而不是在繁琐的过程细节上过多地纠缠[6]。守恒定律的巧妙运用要求教师具有渊博的知识、丰富的教学经验及高超的总揽全局的能力。只要教师认真钻研教学内容，仔细揣摩分析解决问题的思路，发现解决问题的切入点，就可以灵活地运用这种“重过程、巧守恒”的教学策略取得良好的教学效果[7]。