光学软件热分析方法和消热差镜头设计

石 佳,余飞鸿

(浙江大学光电科学与工程学院,浙江 杭州 310027)

1 引 言

光学系统的性能随着温度变化而变化,温度的变化使系统的最佳像面的位置发生偏离,并且破坏原有的像差校正状态。这种由温度变化引起的性能衰减统称为光学系统的热效应或温度效应。

通常,设计一个光学系统时,仅对20 ℃的单一环境温度进行设计。但是如果一个光学系统的工作环境温度变化范围较大,则整个系统的光学、结构参数都会发生较大的变化,从而降低光学系统的成像质量。所以,对于这种在温度范围变化较大的环境中使用的光学系统,需要在设计时就考虑到温度变化造成的影响。即采取一定的手段使光学系统能在一个温度变化较大的范围内保持良好的光学系统性能。

国外对热分析研究起步较早。1981年,Miller[1-2]等人首次提出了热-结构-光集成分析方法(the structure-thermal-optical integrated analysis,STO),它开创性地结合了光学、机械学、热学三个学科,在三者结合的基础上进行了优化设计的循环过程,实现了以集成的观点对光机系统进行分析的目的,揭开了“光机热集成分析”的序幕。1984年,Gibbons[3]通过阿贝曲线进行红外温度自适应系统的设计。1990年,Rayces和Lebich[4]使用了γV-V图,通过选择合适的材料,设计了可以进行温度补偿的三片式光学系统。1991年,Rogers[5]通过试探的方法,寻求无热化光学系统中合适的材料组合。1992年,Yasuhisa Tamagawa等人[6]提出了一种利用T-C图的新方式去寻找同时消热差和消色差的材料组合,并于1994年[7]和1996年[8]利用该方法寻求了合适的材料组合,对红外光学系统进行了无热设计。

国内在21世纪之前对热分析的研究较少,21世纪初,中国科技大学精密机械与精密仪器系[9]、北京理工大学光电工程系[10-12]、北京空间机电研究所[13]、天津津航技术物理研究所[14]、浙江大学[15-19]、华中光电技术研究所[20]、西安应用光学研究所[21-24]、浙江师范大学[25]等单位对光学系统的无热化设计展开了研究,并对红外镜头以及卫星CCD相机等光学系统进行了无热化设计。中国科技大学精密机械与精密仪器系的胡玉禧[9]等人使用T-C图寻求可以互补热差的材料组合,设计了同时消热差和消色差的三片式光学系统。北京理工大学的李林[10]等人研究了环境温度变化对光学系统性能产生的影响,设计了光学热效应分析软件。北京空间机电研究所的黄颖[13]等人论述了遥感卫星CCD相机光学系统的热补偿设计方法。天津津航技术物理研究所的吴晓靖等人[14]将无热化光学系统设计方法与变焦系统设计方法进行类比,将光学系统的无热化设计方法等同于广义变焦的设计方法。浙江大学的奚晓[15-17]等人研究了红外光学系统的无热化设计,文献[15]和文献[16]分别采用了光学被动式无热技术和机械(电子)主动式无热技术进行无热化设计。华中光电技术研究所的杨长城[20]等人研究了折射系统和折/衍射混合系统的无热化设计方法,并进行了红外波段的折射系统和折/衍混合系统的无热设计。西安应用光学研究所的焦明印[21]使用近轴成像公式,推导出光学系统实现热补偿的通用条件。西安应用光学研究所的罗传伟[22]等人提出一种在Code V中分析和计算折射率温度效应的新方案。西安应用光学研究所的王学新[24]等人通过研究消热差方法,提出了光学被动式和机电式组合消热差的方法,即先使用光学被动消热差方法得到合理的消热差材料组合,降低热差,然后剩余像差通过机电消热差的方法消除。浙江师范大学的钱义先[25]分析了航空相机光学系统的无热化设计,使用广义变焦系统的设计方法来进行可见光折射系统的无热化设计。

过去,进行热分析的光学系统大多为红外镜头、航天航空镜头等。随着塑料镜片的广泛使用以及光学系统使用环境的多样化,目前,更多种类的镜头需要在环境温度变化较大的范围内保持良好的光学性能。现在已有较多文献资料对红外镜头、航空航天镜头进行热分析,但对车载镜头、监控镜头等其他种类的镜头的研究资料较少,且目前它们同样需要在较大的温度范围内工作,为了消除温度效应对光学系统产生的影响,需要使用无热技术对系统进行补偿,使光学系统在温度变化范围较大的情况下都能保持较好的成像质量,从而使光学系统能够在较大范围的温度环境下正常工作。

2 热分析的相关知识

2.1 光学元件的热分析参数

1)折射率温度系数dn/dT

折射率与温度有关,单位温度引起折射率的变化称为折射率温度系数。

光学材料的绝对折射率随着温度变化的变化值由式(1)给出,该公式是根据Sellmeier拟合公式推导而来,其中各个系数通过拟合实际材料数据确定:

(1)

式中,n为光学材料在某温度下的绝对折射率；ΔT表示温度的变化量；其他6个常数由材料制造商提供,均为折射率公式的拟合参数,D0、D1、D2的单位分别为℃-1、℃-2、℃-3,E0、E1的单位分别为μm2/℃、μm2/℃2,λtk的单位为μm,一般位于0.08～0.33之间。

将式(1)两边对T进行求导,得到光学材料的绝对折射率关于温度的导数,即绝对折射率温度系数,如式(2)所示:

(2)

2)热膨胀系数

光学材料的热膨胀是指由于温度变化引起的光学材料的热胀冷缩现象,以热膨胀系数α表示,表示在压强一定时,单位温度变化引起的光学材料的长度或者体积的变化,单位为ppm/℃,1ppm=1×10-6。

2.2 光学系统的结构参数变化

1)光学元件的曲率半径、中心厚度随温度的变化

光学元件的曲率半径、中心厚度随温度的变化是由光学材料的热胀冷缩引起的,与光学材料的线性热膨胀系数α0有关[26]。当温度变化后,光学元件的曲率半径和中心厚度变为:

R′=R+dR=R+R·α0·dT

=R(1+α0·dT)

(3)

D′=D+dD=D+D·α0·dT

=D(1+α0·dT)

(4)

式(3)和式(4)中,R,D和R′,D′分别为温度变化前和温度变化后的曲率半径和中心厚度,dT为温度变化量,α0为光学材料的线性热膨胀系数。

非球面示意图如图1所示。二次曲面的面型不会随着温度变化而发生变化,旋转偶次非球面的曲面方程如式(5)所示。

图 1 非球面示意图Fig.1 Aspheric diagram

(5)

式中,h为曲面上的点到光轴的距离；z为该点到顶点的沿轴距离；c为顶点处的曲率；k为二次曲面常量。

非球面的二次曲面常量k不会随着温度变化而变化,顶点处的基本曲率半径的变化如式(3)所示,高次方的系数的变化如式(6)、式(7)、式(8)所示:

(6)

(7)

(8)

……

2)镜片间隔随温度的变化

镜片间隔随温度的变化与镜筒、隔圈等零件材料的热胀冷缩有关。由于光学设计时只考虑镜片间的中心间隔,而镜筒、隔圈的变形会引起边缘间隔的变化,必须将其换算成中心间隔的变化量才能进行热分析和设计。这个变化量可以按照以下方式计算:

假设前一片光学元件的后表面的曲面方程如式(9)所示:

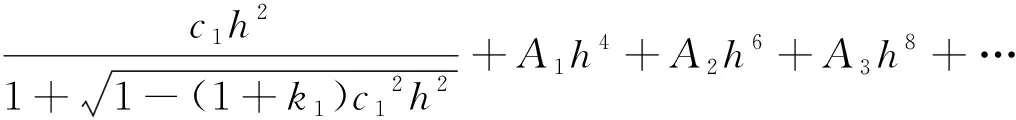
(9)

后一片光学元件的前表面的曲面方程如式(10)所示:

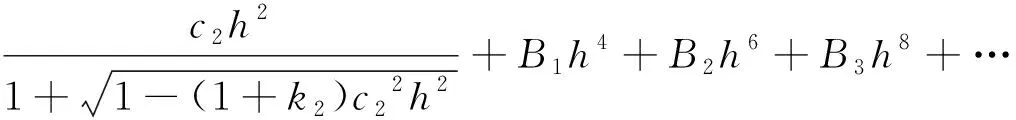
(10)

假设它们之间由一个隔圈隔开,则隔圈与前后两个表面的接触点的高度为H1和H2。在接触点前后两个表面的矢高(即该点与曲面顶点的沿轴距离)分别如式(11)和式(12)所示:

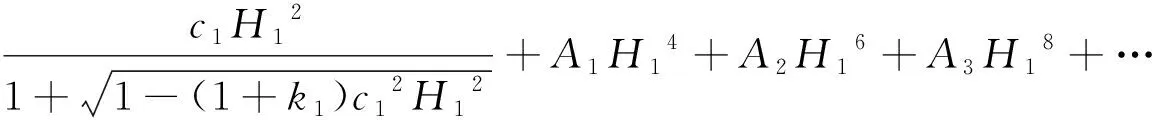
(11)

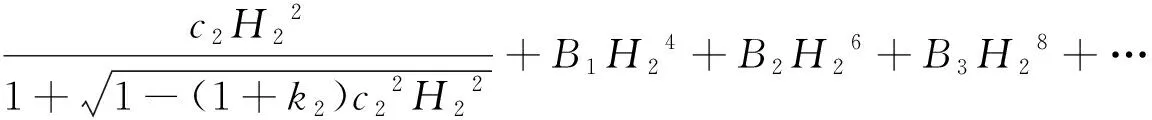
(12)

从式(11)与式(12)可以看出,光学元件的矢高与曲率同号。曲率为正,则矢高大于零；曲率为负,则矢高小于零。隔圈的厚度如式(13)所示:

L=D+z2(H2)-z1(H1)

(13)

式中,L为隔圈的厚度；D为相邻光学元件的中心间隔。

镜片间隔示意图如图 2所示。当温度从T→T′=T+dT时,隔圈的厚度和半直径的变化如式(14)和式(15)所示：

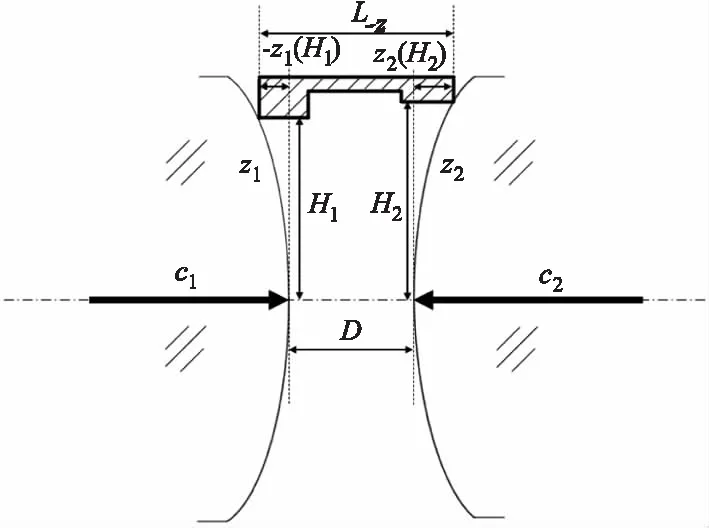
图2 镜片间隔示意图Fig.2 Schematic diagram of lens interval

L′=L+dL=L+L·αm·dT

=L(1+αm·dT)

(14)

H′=H+dH=H+H·αm·dT

=H(1+αm·dT)

(15)

式(14)和式(15)中,L和L′分别为热分析前后的隔圈的厚度,H和H′分别为热分析前后的隔圈的半直径,αm为隔圈材料的线性热膨胀系数。

而在接触点H′处的前后两个表面的矢高分别如式(16)和式(17)所示:

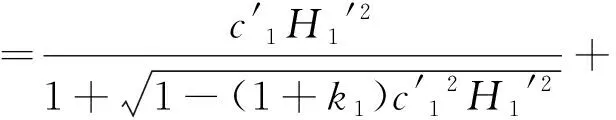
(16)

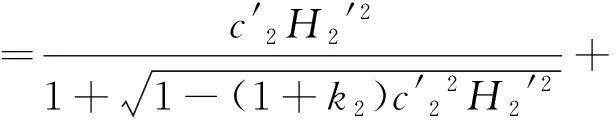
(17)

式(16)和式(17)中,曲面方程中的系数的变化可以参见式(6)、式(7)、式(8)。

因此,温度变化后,两个光学元件的中心间隔如式(18)所示:

D′=L′+z1(H′)-z2(H′)

(18)

上述方程描述了光学系统的热模型,在进行光学系统的无热化设计时,需要利用此模型进行模拟分析,得到不同温度时的成像情况。

3 Code V热分析特点和改进方式

3.1 Code V热分析特点

Code V热分析时,半径变化的计算是基于式(3)和(5),即利用光学元件的热膨胀系数和初始半径计算半径随温度的变化；元件厚度和相邻元件间隔变化的计算是基于式(4)进行计算,即利用光学元件的热膨胀系数和初始元件厚度计算元件厚度随温度的变化、利用隔圈或镜筒的热膨胀系数和初始元件中心间隔计算相邻元件间隔随温度的变化。但是,根据前面所述的光学系统的热模型,计算相邻元件间隔随温度的变化时,需要先计算间隔处镜筒或者隔圈的变形,再将其换算成相邻元件中心间隔的变化量,换言之,相邻元件间隔随温度的变化与镜筒或隔圈的热膨胀以及元件表面形状有关,因此仅通过式(4)计算的相邻间隔变化与实际情况存在一定误差,是不准确的。

光学材料折射率随温度的变化量可以通过两种方法计算:第一,如果Code V玻璃库中包括所需分析材料的热分析参数,则直接利用式(2)计算出材料的折射率温度系数,以此得到光学材料在高温和低温下的折射率,并以自定义材料的形式储存；第二,如果Code V玻璃库中没有包含所需分析材料的热分析参数,则需要在therm_env.seq文件中输入材料的折射率温度系数,以此得到光学材料在高温和低温下的折射率。第一种方法得到的折射率是直接根据材料的热分析参数计算出来的,与实际相近,第二种方法是通过直接输入材料的折射率温度系数进行计算,由于材料的折射率温度系数是温度的函数,所以单凭某一温度下的折射率温度系数计算出来的折射率与实际情况存在一定差异,存在误差,在比较小的温度范围内,折射率温度系数变化较小,因此由此导致的误差可以忽略,但是在温度范围较大的情况下,最高温度对应的材料折射率温度系数与最低温度对应的材料折射率系数相差较大,折射率温度系数的变化不能忽略,因此计算出来的材料在高温时和低温时的折射率与实际情况差异较大,导致在较大温度范围时热分析结果不准确。

3.2 光学元件间隔计算改进

3.2.1 典型装配方式

假设镜片与镜筒之间胶合方式为弹性胶合,在温度升高情况下,当镜筒膨胀的速度比镜片膨胀的速度快时,镜筒和镜片之间产生的间隔会由胶合层填满,如图 3所示,图中展示的是两个相邻表面都是凹面的情况,相邻镜片通过隔圈固定在镜筒中,因此隔圈和镜筒在相邻表面边缘处的轴向长度决定了相邻镜片的中心间隔。

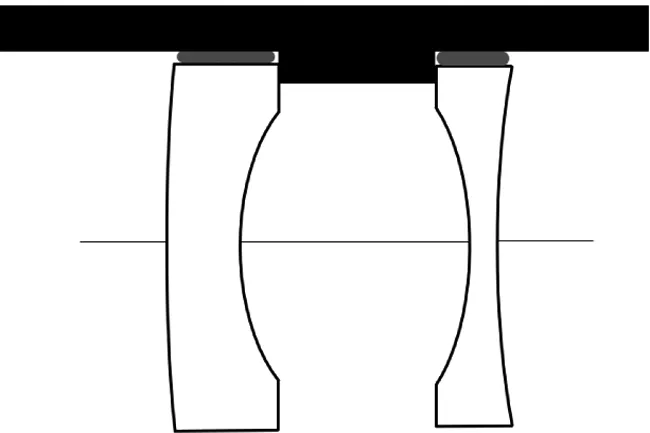
图3 装配方式一Fig.3 Assembly method 1

图3只是展示了最简单的一种装配方式,即镜筒和隔圈与相邻表面相接触,图 4展示了隔圈与不相邻的两个表面相接触的情况,图4中,表面2和表面4的中心间隔是受镜筒的热膨胀系数和接触两个表面的镜筒的轴向长度决定的,而表面2和表面4的表面顶点的位移是由光学材料的热膨胀系数和表面矢高决定,最后通过计算出表面2和表面4的顶点距离,推断出表面1和3的顶点移动距离。

图4 装配方式二Fig.4 Assembly method 2

图5展示了隔圈不与相邻表面相接触的一种特殊情况,此时,隔圈与其中一个表面的凸面相接触,在这种情况下,表面顶点移动距离的计算将会更加复杂。

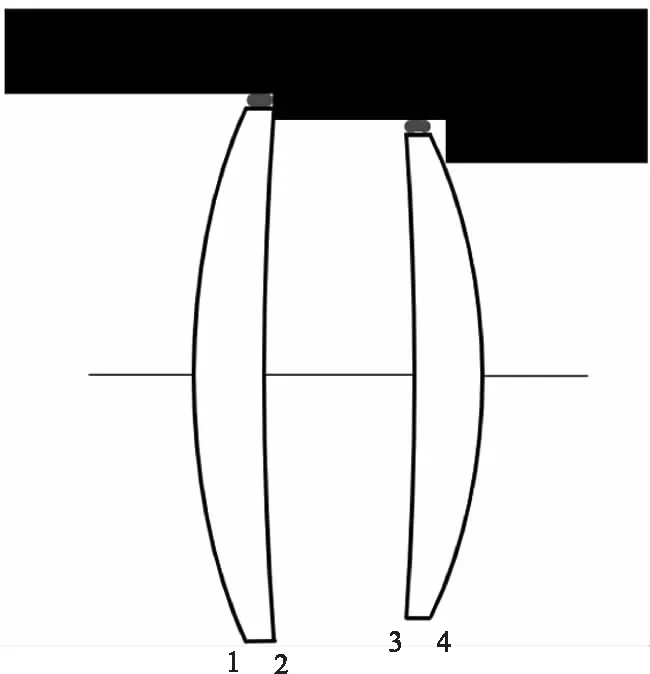
图5 装配方式三Fig.5 Assembly method 3

3.2.2 宏语言编写原理

当温度从当温度从T→T′=T+dT时,镜片的半直径的变化如式(19)所示:

Hg′=Hg+dHg=Hg+H·α0·dTg

=Hg(1+α0·dT)

(19)

式中,Hg和Hg′分别为温度变化前和温度变化后的镜片的半直径；dT为环境温度的改变量；α0为光学材料的线性热膨胀系数。

当温度从T→T′=T+dT时,镜片的半直径的变化如式(20)所示:

Hh′=Hh+dHh=Hh+Hh·αm·dT

=Hh(1+αm·dT)

(20)

式中,Hh和Hh′分别为温度变化前和温度变化后的镜片的半直径,dT为环境温度的改变量；αm为隔圈的线性热膨胀系数。

计算隔圈与镜片接触点处的矢高时,首先需要假设镜片表面与隔圈一直保持接触。在温度升高的过程中,镜筒会在沿轴方向上和垂轴方向上都发生膨胀,此时隔圈与镜片的接触点会远离轴线。

进行相邻元件间隔变化的计算时,需要根据光学系统的热模型,综合考虑镜筒或者隔圈的变形、以及镜片表面形状。图6为相邻两个光学元件的热模型,相邻元件中心间隔与隔圈厚度以及两元件相邻表面矢高的关系式如式(21)所示:

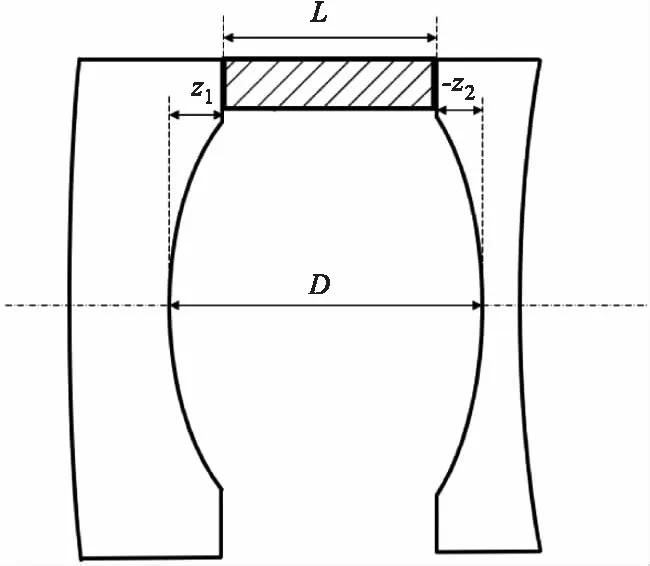
图6 相邻光学元件间隔Fig.6 Schematic diagram of adjacent optical elements

D=L+z1-z2

(21)

其中,D是相邻元件中心间隔；L是隔圈厚度；z1是前一片元件后表面的矢高；z2是后一片元件前表面的矢高。

首先,需要计算镜片半径R、隔圈厚度L和半直径H的变化,计算公式如式(3)、式(14)和式(15)所示。

然后,计算出两个相邻表面各自矢高的变化,如果镜片表面为凹面,则直接利用光学元件的热膨胀系数和原始矢高进行计算,初始镜片表面与隔圈的接触点的矢高如式(22)所示,温度变化后接触点的矢高如式(23)所示：

(22)

z′=z(1+α0·dT)

(23)

如果镜片表面为凸面,假设隔圈和镜片表面保持接触,则温度变化后镜片表面与隔圈的接触点会随着隔圈的热膨胀发生变化,此时该点处矢高如式(24)所示：

(24)

最后根据式(25),将镜筒或者隔圈的变形换算成相邻光学元件间隔的变化量:

(25)

3.2.3 实现方式

为了能计算各元件前后表面的矢高,首先需要确定各元件前后表面边缘的位置,利用Code V内置的sagf()函数得到表面边缘处的矢高,然后在每个表面处插入两个虚拟面,其中一个表面表示边缘处的位置,另一个表面的作用是将当前坐标返回到表面顶点处。

在添加虚拟面时,需要对单透镜、双胶合透镜和光阑等表面进行分情况讨论,以保证每个元件前后表面都正确添加2个虚拟面,并且没有多余的虚拟面存在。

3.3 光学材料折射率计算改进

3.3.1 计算理论

光学材料的折射率温度系数如式(2)所示,图 7给出了几种肖特材料的折射率温度系数随温度变化的曲线。

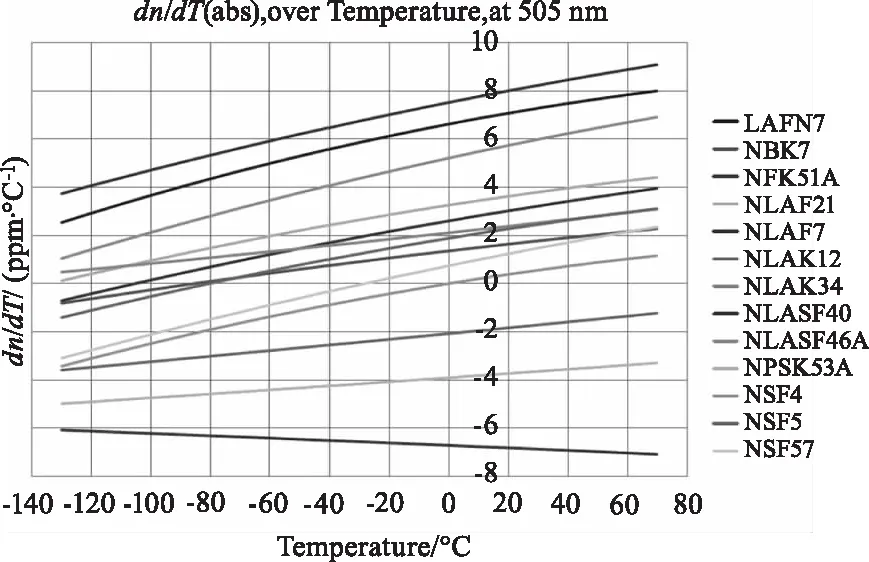
图7 绝对折射率温度系数Fig.7 absolute dn/dT

从图7中可以看出,许多材料的折射率温度系数与温度相关,并且随温度变化会发生较大变化,甚至在-100 ℃至20 ℃之间许多材料的折射率温度系数的正负号发生了变化。因此,在一个较宽的温度范围内仅仅运用20 ℃时的折射率温度系数得到的结果是不准确的。为了解决这个问题,可以分别计算出各个温度下的折射率温度系数,再依次进行计算各个温度下的折射率,具体而言,就是从20 ℃开始,利用式(2)计算出20 ℃时的折射率温度系数,然后利用20 ℃时的折射率和折射率温度系数,计算出19 ℃时的折射率和折射率温度系数,再利用19 ℃时的折射率和折射率温度系数,计算出18 ℃时的折射率和折射率温度系数,重复步骤直到达到所需分析的最低温度,然后再从20 ℃重新开始,利用20 ℃时的折射率和折射率温度系数,计算出21 ℃的折射率和折射率温度系数,重复步骤直到达到所需分析的最高温度。在此过程中,可以减小计算温度的间隔以进一步提高精确性。值得注意的是,在图 7中可以看出,许多材料在温度0 ℃以下时,其折射率温度系数小于零,这就有可能导致在低温时,该材料的折射率甚至小于20 ℃时的折射率。

3.3.2 宏语言编写原理

在Code V软件中,对于软件内未包含热分析参数的材料,不能直接使用添加的光学材料的热分析参数直接计算不同温度下的折射率,而需要通过计算光学材料在指定温度下的折射率温度系数从而获得不同温度下的折射率。

Code V软件计算塑料材料不同温度的折射率的步骤如下:

①在dndt_constants.dat内添加所缺少的材料的折射率系数与温度系数；

②利用dndtcalc.seq宏计算材料的折射率温度系数；

③将计算所得的折射率温度系数值添加到therm_env.seq宏内；

④利用thermpik.seq宏进行热分析,生成多个温度配置。

⑤根据上述光学材料折射率的计算理论,自定义宏文件,实现读取光学材料的热分析参数,并计算出材料在各个温度下的折射率温度系数,然后进一步推导出材料在高低温时对应各波长的折射率,利用计算的数据生成新的自定义材料,并替换运行thermpik.seq宏时自行生成的材料。

3.4 镜头热分析优化步骤

假设需要进行无热化设计的光学系统的使用温度范围是-20 ℃～85 ℃,则在无热化的设计过程中,选出三个温度作为三个变焦配置的温度,通常情况下选择常温20 ℃、最高温度85 ℃和最低温度-20 ℃,即初始变焦配置的温度设置为常温20 ℃,第二、第三变焦配置的温度分别设置为最高温度85 ℃和最低温度-20 ℃。

然后,将不同变焦配置之间建立起联系,即建立不同变焦配置中镜片的半径、厚度、间隔和材料之间的联系。可以使用Code V中PIK命令建立各个配置之间的联系。由于Code V中PIK命令只能设置线性关系,因此需要对上述间隔计算公式进行近似。将矢高变化都近似为凹面时的情况,如式所示。此时,矢高随温度线性变化,可以使用Code V中的PIK命令对不同温度下矢高建立联系。

镜片元件间隔厚度随温度线性变化,在程序中,具体的命令语句如下:

pikthis^sz^zthis^sz1 ^r0

thi为厚度,^s为表面序号,^z为配置编号,^r为[1+(第^z配置温度-初始温度)×热膨胀系数]。

在进行热分析并修正光学材料的折射率之后,需要对镜头的三个变焦位置(三个不同温度下的系统)进行优化设计。

1) 核对镜头数据,将各镜片的半径、厚度和间隔厚度设置为变量。

2) 修改优化函数,因为插入虚拟面之后原先实际镜片的表面序号会发生改变,因此需要进行调整以保证能正确优化。

3) 添加边缘间隙自定义约束,因为在插入虚拟面后,一般约束中的最小边缘厚度设置不能正确约束边缘间隔,所以需要添加自定义约束以控制各镜片边缘间隙满足加工要求。

假如第i面为前一组镜片的后表面,第j面为后一组镜片的前表面,则边缘间隙自定义约束如下,表示第i面到第j面的边缘间隔:

@ET_i_j==(ETSi)+(OALS(i+1)..(j-1))+(ETS(j-1))

4) 添加误差函数权重进行优化,对三个配置(三个不同温度下的系统)的像质进行优化,使得在整个工作温度范围内系统像质均满足要求。

5) 将添加的虚拟面删除。

6) 重新计算优化后镜头各元件表面的矢高,并添加虚拟面,再次进行镜头的热分析。

7) 检查镜头在整个温度范围内的像质,如果不满足要求,则重新进行第五步和第六步,如果满足要求,则完成镜头的无热化设计。

4 消热差镜头的优化设计

4.1 设计指标

根据设计规格要求,镜头的设计参数如表1所示。

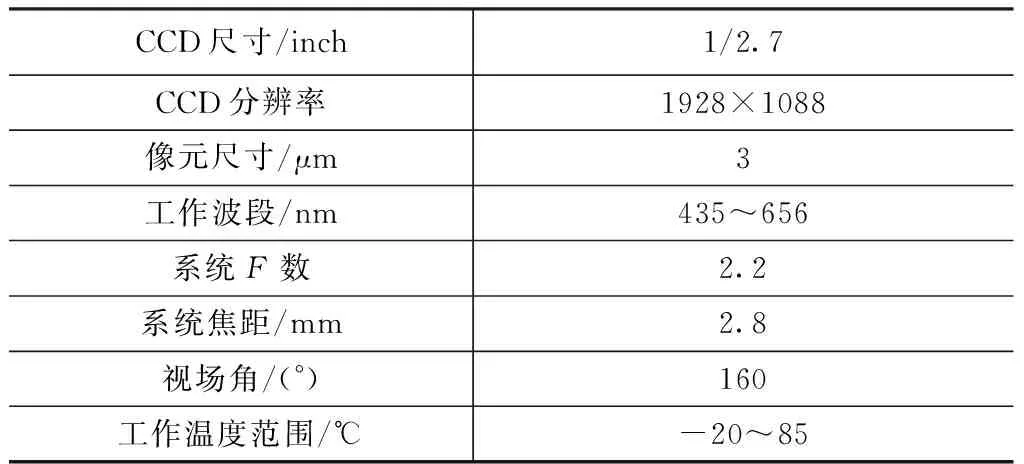
表1 消热差镜头的设计指标Tab.1 Specifications of the athermal lens

4.2 Code V无热化分析和优化结果

根据设计指标,选取合适的初始结构,利用Code V软件进行优化,然后通过改进的Code V热分析优化方式进行无热化设计,无热化镜头的最终优化设计结果如图8所示。

图8 消热差镜头的二维图Fig.8 2D plot of the athermal lens

经过无热化优化设计,镜头系统各个波段在-20 ℃～85 ℃温度范围内成像质量良好。图 9(a)、(b)和(c)分别为温度为20 ℃、-20 ℃和85℃时的MTF曲线。可以看出当温度为20 ℃时,各视场的MTF曲线在160 lp/mm处均大于0.3,高温情况比低温情况的MTF稍差,在温度为-40 ℃时,边缘视场的MTF在160 lp/mm处降至0.24,60°以内的视场的MTF在160 lp/mm处仍在0.4以上,在温度为85 ℃时,边缘视场的MTF降至0.16,60°以内的视场的MTF在160 lp/mm处仍在0.3以上。

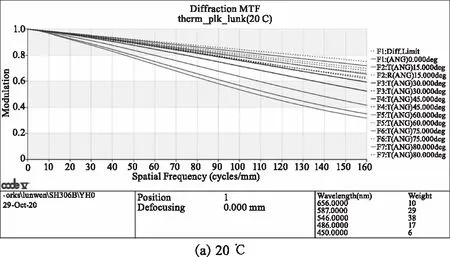
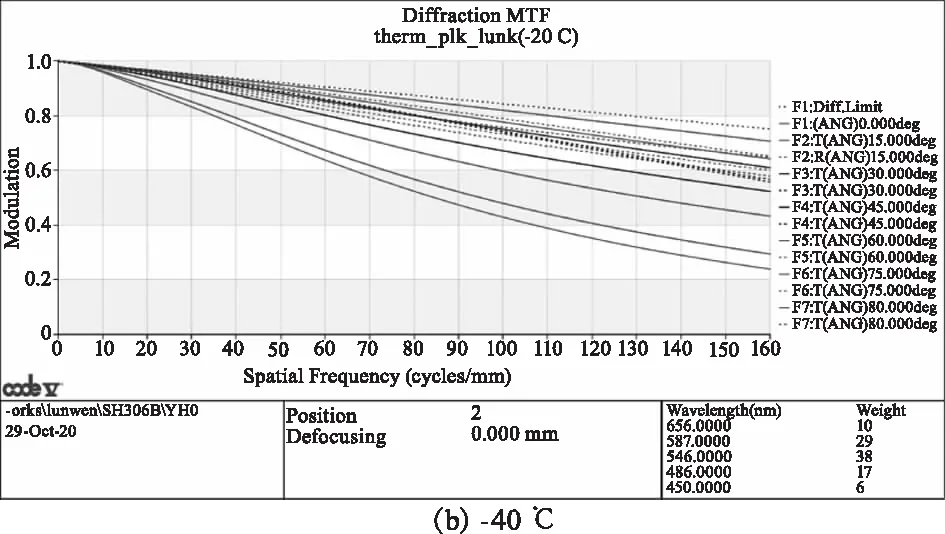
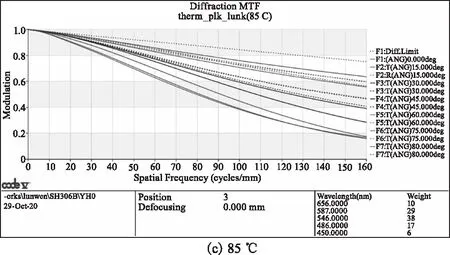
图9 消热差镜头的MTF曲线Fig.9 MTF of the athermal lens

根据瑞里判据,点列图的RMS直径需要小于两倍像元尺寸,相邻两个像点才能被分辨。图 10(a)、(b)和(c)分别为温度为20 ℃、-20 ℃和85 ℃时的点列图,可以看出当温度为20 ℃时,各视场的点列图的RMS直径小于3 μm,各个像点之间可以被传感器所分辨,当温度为-20 ℃或者85 ℃时,各视场的点列图的RMS直径基本在两倍像元尺寸以内,即小于6 μm。因此,成像质量满足传感器的分辨率。

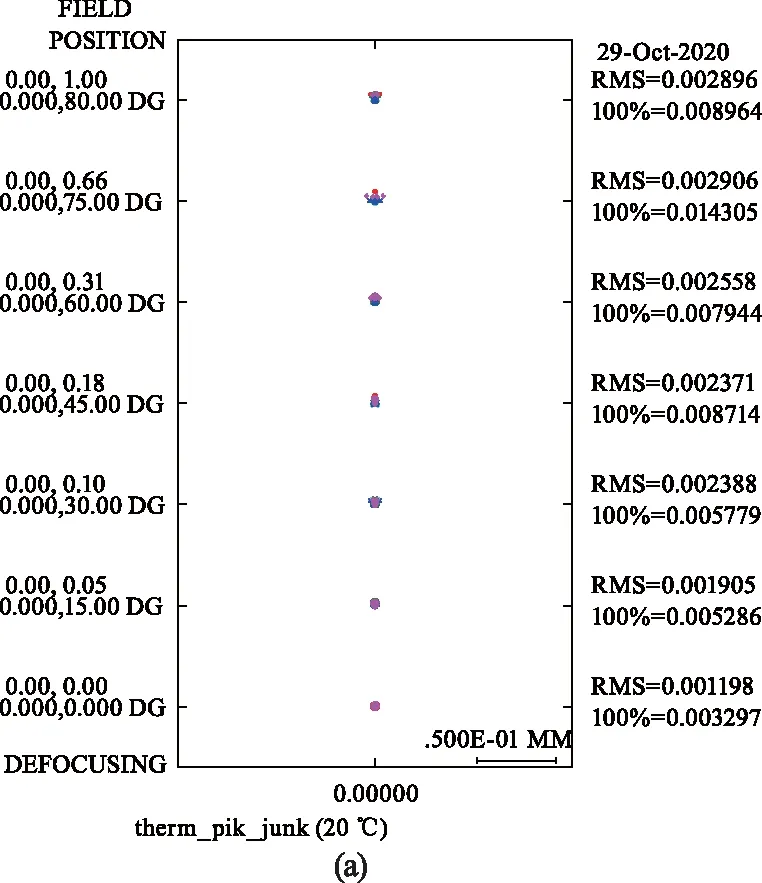
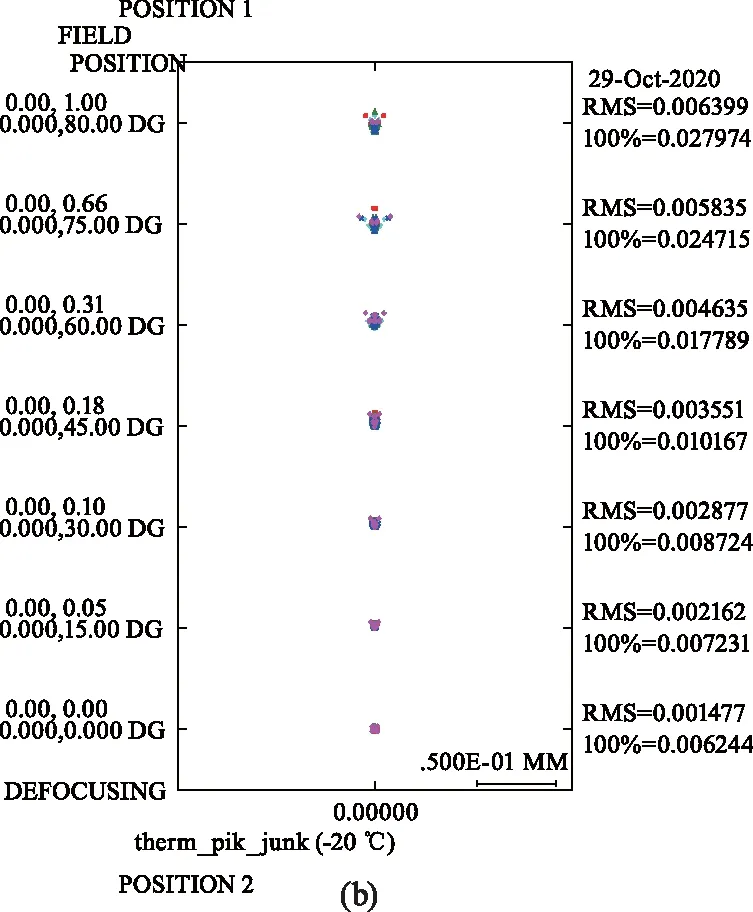
图10 消热差镜头的点列图Fig.10 Spot diagram of the athermal lens

5 总 结

本篇文章主要说明了光学系统热分析和无热化设计方法的相关知识,首先介绍了光学元件的热分析参数,分析了光学系统结构参数随温度变化的情况,然后指出了Code V软件在热分析功能上的不足之处,从光学元件间隔计算和光学材料折射率计算两个方面说明了计算理论,并且利用软件的宏语言进行编写实现,最后使用Code V软件进行了消热差镜头的优化设计,设计结果在-20 ℃～85 ℃之间成像质量良好,完成了镜头的无热化设计。