高校毕业生就业趋势邻接树分析方法研究

李兆飞，熊兴中，汤勇，Volchenkov Dimitry

（1.四川轻化工大学自动化与信息工程学院，四川 宜宾 644002；2.人工智能四川省重点实验室，四川 宜宾 644002；3.比勒费尔德大学先进认知交互技术中心，德国 比勒费尔德 D-33718）

引 言

随着20世纪90年代末中国高等教育实行扩招政策以来，高等院校毕业生数量持续增长，社会就业岗位需求相对不足，毕业生教育结构、就业观念与市场需求脱节的结构性矛盾仍然突出，毕业生就业工作面临极大压力［1］。高等院校毕业生的就业情况是国家及地方各级主管部门、学校和社会都非常关心的问题。高等院校毕业生信息数据库涵盖了高等教育环境的各个方面，能提供对各级教育机构目前状况的一个意义深远的观察，通过对其分析，可以帮助指导专业建设和有针对性的课程改革，能预测复杂的教育系统发展的未来趋势。然而，高等院校毕业生信息数据库包含海量、结构异构、不同度量和非度量的阵列统计数据，如何从这些模糊、有噪声、不完全、随机、事先无法预知却又成倍增长的潜在有用的“大数据”信息中获取有价值的知识是目前亟需解决的问题。

传统上用于高等院校毕业生就业趋势分析系统的数据处理方法，使用简单的SQL 语句进行数据库查询及基本的数据统计［2-4］，并通过简单的图表进行可视化展示。这种方法虽然便于直接比较，但并没有提供高等教育系统的综合情况，其分析方法和呈现方式单一。目前，针对毕业生就业数据挖掘较多采用的技术主要是决策树算法、神经网络算法、关联规则算法和模糊集方法等。如文献［5］基于修正函数和属性优先值的改进ID3算法，从时间复杂度和准确度方面进行毕业生数据挖掘。文献［6］通过对ID3 算法生成毕业生就业分析模型并进行剪枝优化。文献［7］基于云服务决策树分类算法提高了大学生思想政治教育效率。文献［8］采用ID3 算法生成就业预测决策树模型进行就业决策分析。文献［9］采用K-means 聚类分析和R-C4.5 决策树方法挖掘影响高职毕业生就业质量的相关因素。文献［10］基于变精度粗糙集的决策树模型进行就业数据分析。但是这些决策树方法计算量大，产生的决策分类规则鲁棒性较弱。文献［11］采用元分析方法对就业结果的影响进行了分析，但该方法本质上也是统计的方法，呈现方式单一。文献［12］通过减少频繁项集生成的数量，进行候选项集剪枝效率优化的改进Apriori算法，提高了算法的时间和空间复杂度，并应用于职业高中的教学评价与就业分析中。文献［13］通过Apriori 算法在属性选择过程中进行数据预处理量化操作，然后进行对象聚类，得到支持度和置信度，形成对高校的就业分析规则。文献［14］利用代价敏感的非频集过滤矩阵寻找k-频集构造过滤矩阵的Apriori 算法，进行高职院校就业数据挖掘。文献［15］采用关联规则挖掘Apriori 结合ID3 算法，对嘉华学院学生就业进行了分析。但是，无论怎么改进Apriori 算法，都会产生大量的中间项集，适应性较窄。因此，为满足对高校毕业生就业系统数据库几十万，几百万，甚至上亿条多样化和异构的毕业生信息数据进行挖掘分析及呈现的需求，必须建立一种先进而有效的毕业生就业趋势分析系统的数据处理及呈现方法。

基于此，通过研究提出一种统计频率特征距离的高校毕业生就业趋势邻接树分析方法。该方法通过对不同度量和非度量的海量、结构异构的阵列统计数据，引入离散分布（图）来合理的表征“待分析类别”间的距离，并基于相应分布的待分析类别之间的距离矩阵，进一步采用聚类分析技术进行定量多标准比较、分析。

1 方法和设计

提出的统计频率特征距离的高校毕业生就业趋势邻接树分析模型构建中，首先选择一个“待分析类别”，而所有“比较特征”都是随机变量，通过比较特征的离散概率统计分布（由随机变量的值及其相应的概率组成）来描述待分析类别的特性并快速进行傅立叶变换（FFT）；然后，通过待分析类别的频域分布间的Wasserstein 距离（采用两个向量间的标准欧几里德距离）进行量化计算，得到待分析类别间的对称相似距离矩阵, 定量、多标准地进行待分析类别的比较；最后，通过比较待分析类别聚类分析的邻接生成树的形式，对高校毕业生现状进行可视化表征。构建的数据分析算法流程如图1所示。

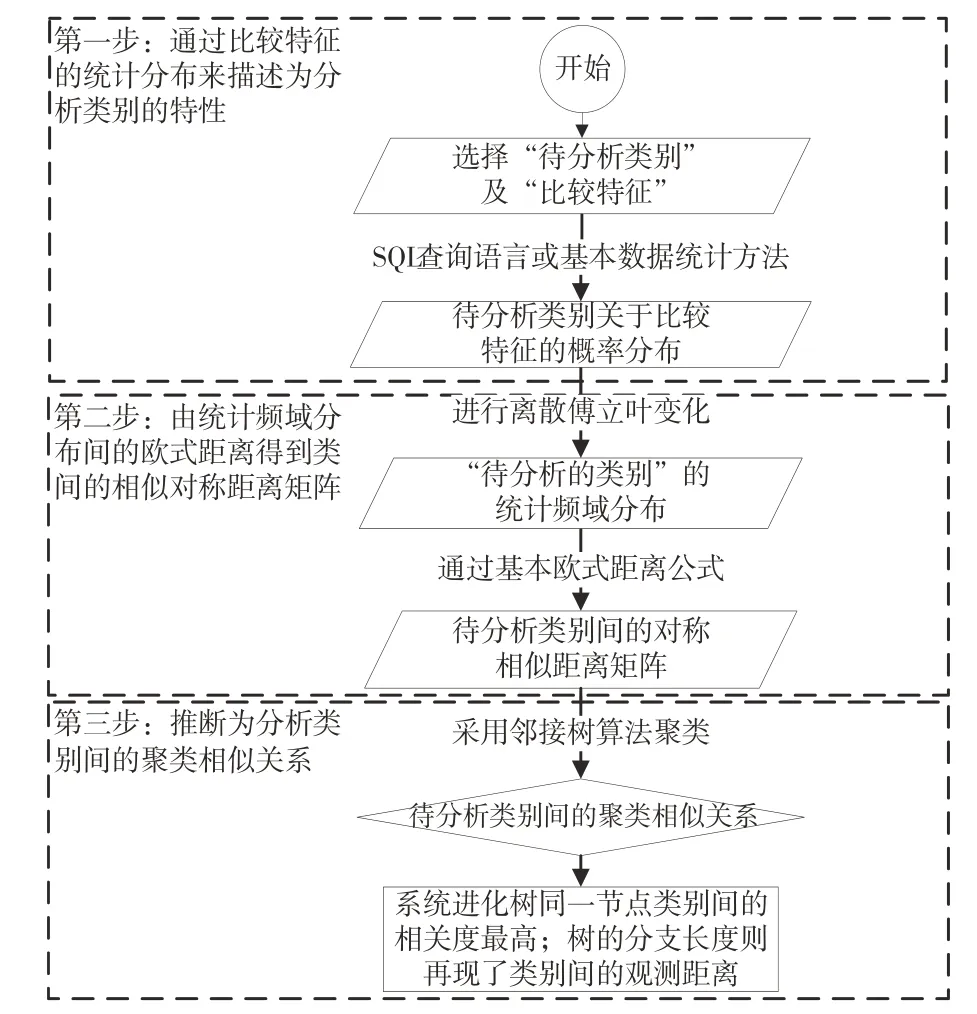
图1 高等院校毕业生就业趋势数据分析算法流程图

1.1 表征待分析类别间的特征分布

由于图表是一种极好的工具，可以直观地比较不同类别（如高校）的产品成果和其他重要特征，因此，该步骤中对“待分析的类别”（也称为“类、分类”或者“被观测特征”，如“高等院校”）的每一个值，考虑每个相关的其他特征（如“专业”、“毕业生去向”和“工作单位类别”等，称为“比较特征”）都是随机变量X。X 作为一种可能的文本值（状态）具有X1,X2,…,Xn多种，则作为分析的类别，其概率也有多种情况P(X1),P(X2),…,P(Xn)。离散概率分布（通过常用的SQL 语言或者相关统计算法实现）由随机变量X 的值及其相应的概率P(X ) 组成，通过图能得到体现。最终，从数据库中就可以直接计算待分析的类别（如“高等院校”）的文本值或状态的经验分布。例如，如果选择的类别是“院校”，选择比较的特征是“就业单位行业”，那么部分院校毕业生就业单位行业可能的最终等级分布情况如图2 所示。该方法具有可伸缩性、实时性、跨平台性，允许与潜在的数据库（如包括数十亿个人信息的数据库）同时工作。

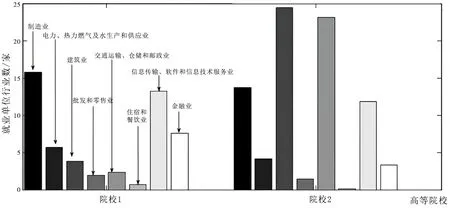
图2 部分院校毕业生就业单位行业可能的最终等级分布（从左到右依次排列）

1.2 通过离散傅里叶变换计算分布向量间的距离

虽然图表便于对待分析类别进行直接比较，但并没有提供整个高等教育系统的综合情况。因此，通过引入离散分布（图）来合理地表征待分析类别之间的距离，将有助于进行大规模的数据聚类分析。但该方法的主要问题在于数据库中特定状态的文本数据不构成度量空间，因此直接使用标准概率度量作为图之间距离的方法不可取。在Volchenkov Dimitry 之前的研究中［16-19］，常把离散分布图视为由图表示的信号，形成了对非度量结构数据集的分析技术。对图上定义的扩散过程的谱分析，能够基于自回避随机游动的第一通道时间方法定义结构化数据集上的度量。该框架扩展了Wasserstein 度量的概念，Wasserstein 度量被定义为两个概率分布在一个给定的度量空间的距离，如果是非度量空间则辅以图形结构进行定义［20］。如果每一个分布被视为在顶点堆积的一个单位数量的“沙”，这样的度量就是随机行走者将一堆沙变成另一堆沙的最小“成本”（时间步长）。由于描述可能的文本值（状态）给待分析类别之间的精确图形结构关系未知，该步骤中假设它是一个完全图，如图3所示。

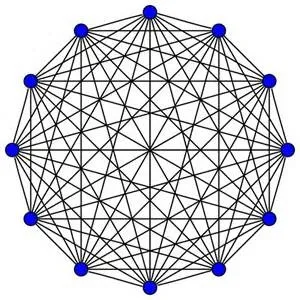
图3 文本值（状态）与待分析类别之间的完全图结构

完全图上定义的信号的谱等价于离散傅立叶变换（DFT），可以用酉DFT矩阵的形式表示如下：

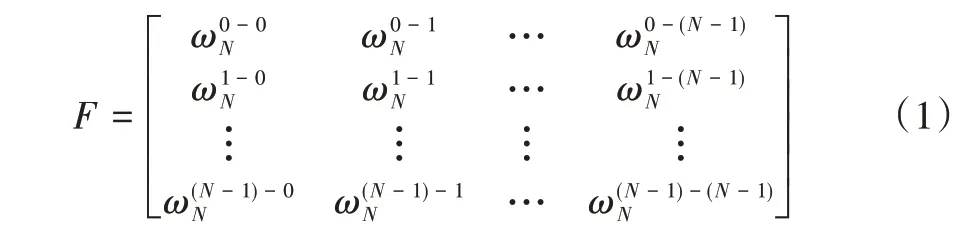
式中，ωN= e-2πiN，i 为虚数单位，e 为自然对数底数，N 为数据个数。利用DFT，每个由图表示的采样信号yk（特别是直接从数据库中计算状态的分布）能被分解成频域中的傅里叶模式Yk。

离散傅里叶逆变换如式（2）所示：

式中，N 为数据点个数，n 为变换点数，Yk为DFT 变换后的数据，k = 0,1,…,N - 1，在频域中傅立叶变换的振幅采用下式计算得到：

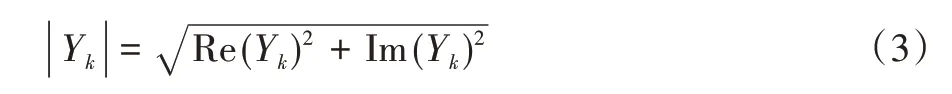
式中，Re(Yk)和Im(Yk)分别表示Yk的实部和虚部， || Yk为频域中傅里叶变换的振幅，分布的DFT 可以视为一个坐标变换，它只是简单地指定一个新坐标系中向量的分量，保 持 点 积 和 向 量 范 数y = (y1,y2,…,yn) →y͂=(Y1,Y2,…,Yn)。

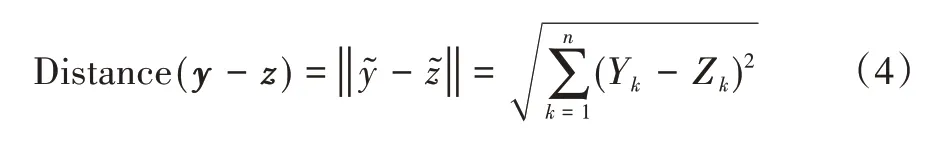
DFT 的正交性对于该算法框架是最重要的，因为它允许使用两个向量之间的标准欧几里德距离作为Wasserstein度量，标准欧式距离公式如下：式中，Distance(y - z ) 表示两个向量y 和z 间的欧式距离表示两个向量y 和z 编码后的向量y͂和z͂间的欧式距离，Yk和Zk为y 和z 经DFT 变换后的数据。为了评估向量y 和z 编码后的两个分布之间的距离，该算法框架中定义的距离为分布矢量中的对齐位置的不匹配分数。并且采用快速傅立叶变换（FFT）得到频域的处理过程，解决数据特征尺度的统一问题，就可以使用统计特征分布间的标准欧式距离进行量化计算，从而得到待分析类别间的对称相似距离矩阵。

离散傅立叶变换在很多领域都有广泛的应用，并且有著名的快速算法（快速傅立叶变换），有效地用于计算离散傅立叶变换。本文提出的方法通过离散傅立叶变换计算分布之间的距离，具有统计鲁棒性，能够容忍部分不完整和伪造数据，使其可以用于不同的计算平台且易于实现。

1.3 邻接树算法推断待分析类别间的相似距离

由于采用DFT 计算待分析类别（如院校）之间的距离，得到了描述每两个待分析类别之间距离的一个对称的、实值的、零对角的矩阵，基于相应分布的类别之间的距离矩阵，可以进一步采用各种聚类分析方法。本研究采用了系统进化树的聚类形式，将密切相关的类别（如院校）置于同一个内部节点，其分支长度紧密再现了相关类别之间的观察距离。特别地，使用邻接树方法［21］将一般数据聚类技术通过给定的距离，作为一个聚类度量应用于序列分析。邻接算法拓扑结构相当于一个星型网络，从一个完全不具备决断能力的树，通过连接最近矩阵中欧式距离最近的元素进行迭代，直至树具有判断的功能。并且，树中所有分支的长度是已知的，分支（花穗）长度表明按照指标或选择特征对数据的分级及排名（拟合优劣程度）：分支越短，表明（与线性排序的距离矩阵）契合度越好；分支越长越远，拟合度及关联度越低，说明就业或单位等情况越不好。在每一步的近邻连接贪婪的加入这对分类树，最大限度地减少生成的邻接树的长度（分支长度的总和，距离矩阵中距离数值的一个特殊加权和），最终，生成一个接近最优的拓扑结构。

该步骤中，采用邻接数算法对分析大型数据集（数百个或数千个分类单元）具有快速而实用的优点，并且有许多可用的程序实现该算法，使该方法在不同的计算平台可行且易于实现。也使分析结果可以实现直观明了的可视化表征，解决了决策者对待分析类别间的相似关系进行决策处理的困难，并且具有快速和鲁棒分析的特点。

2 试验结果及分析

研究对象为四川省教育厅就业指导中心提供的截至2016 年8 月底的2016 届毕业生就业信息数据库（包含了390 000 多条省级高等院所毕业生信息）。该数据库是一个矩形表，包括字段为：学籍信息（民族，政治面貌，学历，专业，专业方向等），就业信息（毕业生去向，就业单位名称，就业单位组织机构，就业单位性质，就业单位行业，就业单位所在地，工作职位类别），派遣信息（报到证签发类别，报到证签往单位名称及签往单位所在地）及报到证信息（报到证编号和报道起始时间）等。提出的统计频率特征距离的高校毕业生就业趋势邻接树分析方法中，统计特征选择主要的14 个文本列或字段为：高等院校名称、性别、政治面貌、学历、专业、生源所在地、学制、师范生类别、困难生类别、毕业生去向、就业单位行业、就业单位性质和工作职位类别及签往单位所在地，每个列或字段中的每个记录可以仅用几个文本值来表示，例如，在列的“就业单位行业”，该值可以是采矿业、制造业、建筑业等。

对该数据库基于高等院校作为“待分析特征”，分别选择毕业去向、就业地域类型、就业省份分布、就业行业分布、就业职位分布及就业单位性质进行了分类研究，由于篇幅所限，这里只给出了部分研究分析结果。

2.1 毕业去向分布实验

由四川省2016届毕业生信息，统计了120所高等院校学生毕业去向（包括：签就业协议形势就业、科研助理、待就业、自主创业和升学等14种毕业去向）的分布。通过分析，大多数院校毕业生以签劳动合同形式、签就业协议和其他录用形式就业为主。通过本文所提出的算法，得到各高等院校毕业生去向的整体聚类结果如图4所示。

图4 中，所生成的辐射树左边部分高校（四川大学、四川文理学院、四川化工职业技术学院）毕业生的毕业去向分布拟合最差（即该类高校毕业去向分布最分散）；图4 中下边“灯泡”状部分高校（西南财经大学、四川职业技术学院及四川工业管理职业学院）表示高等院校集团，这部分高等院校的毕业去向分布杂乱无章，很难区分优劣，但这部分学校中有两类高校（四川邮电职业技术学院到四川工程职业技术学院为一簇，四川外国语大学成都学院到四川工业管理职业学院为另外一簇）具有较相似的毕业去向分布。图4 中右上方分支部分高校（四川大学锦城学院到中国航空研究院611 研究所等）就业毕业去向分布拟合较好（即该类高校就业毕业去向分布较集中）；图4 中最右上方部分高校（中国燃气涡轮研究院到等中共四川省委党校）就业省份分布拟合最好（即该类高校就业类型分布最集中）。

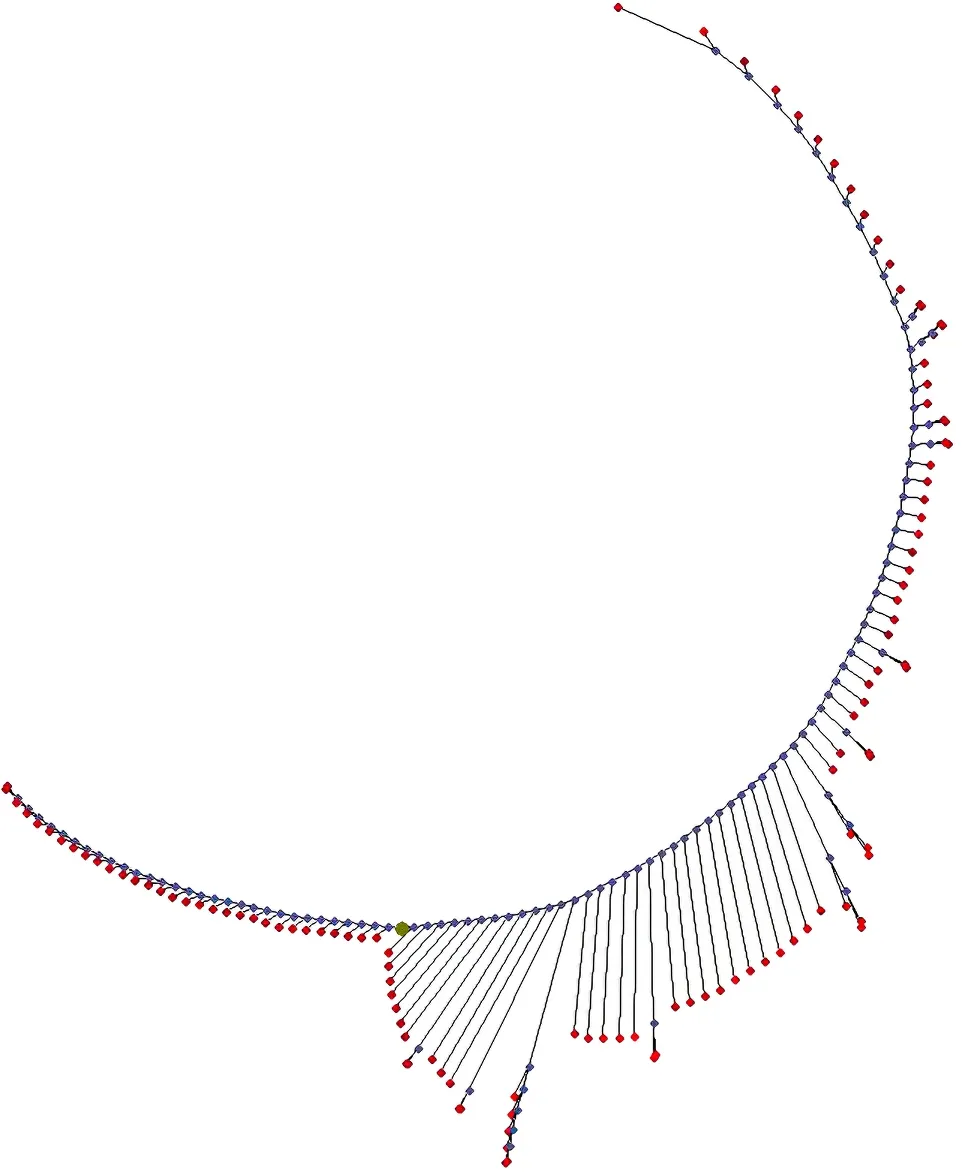
图4 高等院校毕业生毕业去向的聚类结果

2.2 就业地域类型分布实验

由四川省2016届毕业生信息，统计120所高等院校毕业生的就业地域类型（包括：直辖市、省会城市、计划单列市、地级市和县级市6 种地域类型）的分布。通过分析，大多数院校毕业生就业最多的地域是省会城市，其次是地级市。通过算法得到各高等院校毕业生就业地域类型的整体聚类结果如图5所示。

图5 中，所生成的辐射树最右边的族，分别为核工业西南物理研究院、西南通信研究院、西南技术物理研究院、中共四川省委党校、西南自动化研究所、电信科学技术第五研究所、中国核动力研究设计院及中国燃气涡轮研究院在同一个节点下，表明这些高校具有相似的就业地域类型，该部分高校就业地域分布拟合较差（即该类高校就业类型分布较分散）。左上方“灯泡”状部分（四川托普信息职业技术学院、四川师范大学文理学院及成都职业技术学院等）表示高等院校集团，这部分高等院校的就业地域类型分布杂乱无章，很难区分优劣。右上方分支部分如四川大学、四川音乐学院、川北医学院等高等院校毕业生的就业地域分布拟合最差（即该类高校就业类型分布最分散）。图5 中，“灯泡”状下边部分高校（四川商务职业学院、四川艺术职业学院及四川西南科学大学城市学院等）就业地域分布拟合较好（即该类高校就业类型分布较集中）。图5 中最右下方部分高校（中科院成都生物研究所、中国科学院光电技术研究所及中科院成都计算机应用研究所等院校）就业地域分布拟合最好，即该类高校就业类型分布最集中。

图5 高等院校毕业生就业地域类型的聚类结果

由于篇幅所限，高等院校作为“待分析类别”对其它比较特征（如就业省份、就业行业及就业单位性质等）可以进行类似的分析。同时，也可以选择毕业去向、就业地域类型、就业省份、就业行业及就业单位性质等作为“待分析类别”，其它特征或字段作为比较特征对高校毕业生相关数据进行聚类分析。

3 结束语

基于统计频率特征距离的高校毕业生就业趋势邻接树分析方法的研究，及对四川省2016 届毕业生数据库的部分待分析类别的研究分析表明，该方法可以实现省级或国家高等教育系统数百万大学毕业生大规模数据的研究分析（数据规模越大，效果越好），其算法效率及可视化效果优于单纯用SQL 语言进行数据库查询并通过图表呈现的方式。该方法比决策树算法计算量小，决策分类鲁棒性更强；也较Apriori 算法简单、分析效率高，是一种先进而有效的方法。能解决教育主管部门及相关机构进行大数据挖掘及战略决策困难的问题，也可用于经济、社会保障、卫生保健系统等各种大规模统计数据库的分析，具有较好的应用前景。