施工横通道交叉口射流风机布置方式优化研究

聂清文

（中铁十二局集团第一工程有限公司 陕西西安 710038）

1 前言

射流风机在隧道施工通风中具有射流、卷吸和诱导风流的作用。在长大隧道施工过程中，单一的压入式通风方式不足以稀释大量有毒有害气体和粉尘，往往需要通过布置射流风机进行辅助通风［1－3］。我国对于射流风机辅助通风的研究起步虽然较晚，但经过学者们的不断努力仍积累了一定的成果。

目前对于射流风机辅助通风的研究主要可分为特殊隧道环境下射流风机的应用研究和射流风机的优化布置研究两个方面。在特殊隧道环境下射流风机的应用方面，李景银［4］系统讨论了射流风机的参数、推力计算公式并针对高海拔地区研究风机的设计要点。王峰等［5］分析了小半径曲线隧道射流风机布置方式对风机升压折减效率的影响。康小兵等［6］针对高瓦斯隧道研究了射流风机的合理布置方式。方勇等［7］研究了低瓦斯隧道射流风机辅助通风技术。上述研究极大地拓宽了射流风机在隧道通风中的应用范围。

在射流风机的优化布置方面，戴国平等［8］对射流风机在公路隧道中的应用及选型进行了系统分析。冯炼［9］结合新龙门隧道污染物浓度分布对射流风机的送风方向进行了研究。王海桥等［10］建立独头巷道压入式受限附壁射流通风的紊流k－ε数学模型，研究了射流通风典型截面的流场规律。曹正卯等［11］研究了全射流诱导式通风中多种射流风机组合布置形式对升压效率的影响。上述研究为射流风机在隧道通风组织中的布置选型提供了较为科学的参考，但在这一领域仍存在很多需进一步研究的地方。

压入式通风的极限距离为5 km，单头掘进3 km以上巷道式通风比压入式通风更节能。在隧道巷道式通风中射流风机布置在隧道主洞与施工（车行）横通道交叉口处，于交叉口处形成汇流三通和分流三通，已有研究［12］表明三通局部阻力损失与总管和支管间的夹角、面积比及流量比有关，对此种汇流形式目前尚缺乏足够的理论依据，需要采用试验和数值模拟的方法来研究。因此本文将基于FLUENT流体分析软件，讨论交叉口处射流风机的布置位置和角度，并提出射流风机的最优布置形式。

2 数值计算方法及原理

2.1 模型参数

以成昆铁路老鼻山隧道为依托工程，隧道几何模型尺寸如图1所示。利用FLUENT前处理软件Gambit建立主洞与施工横通道（车行横通道）交叉口射流风机三维通风模型。主洞长度为100 m，施工横通道长度为80 m，交叉口位于主洞中部，如图2所示，射流风机参数如表1所示。

图1 横断面模型（单位：m）

表1 射流风机参数

根据模型特点选择分区划分方式，所用网格类型有Cooper及Hybrid两种。体网格元素主要为四面体网格和六面体网格。在隧道主洞和横通道周边区域网格尺寸为1.2 m，在主洞和横通道交叉口网格加密为0.3 m。网格划分完成后共有30 234个节点、91 283个单元，模型如图2所示。

图2 隧道主洞模型

选取标准K－ε两方程紊流模型，速度－压力耦合采用SIMPLE算法。定义边界条件为：入风口为速度入口边界条件，速度 v＝3 m／s；出风口为压力出口边界条件，初始压力p＝0 Pa；射流风机进口为速度入口边界条件，速度v＝30 m／s；隧道及风管管壁边界类型均为壁面边界，满足无滑移条件，壁面摩阻系数设为0.015；所有压力值的相对压力取为0，即没有附加压力。

2.2 计算工况

施工横通道作为主洞通风联络通道，在隧道施工过程中，主要有两种风流组织形式，如图3和图4所示。

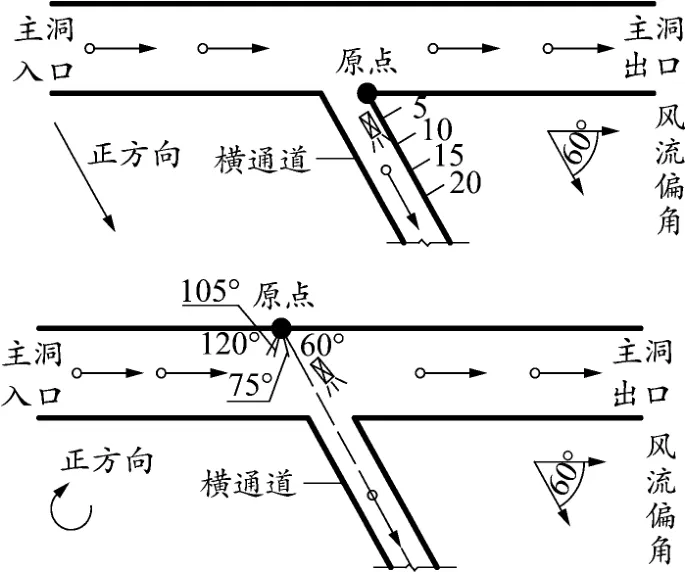
图3 工况1计算模型示意

图4 工况2计算模型示意

2.3 计算原理

射流风机和轴流风机通风的隧道流场可简化为三维粘性不可压缩流场。不可压缩粘性流体的雷诺平均Navier-Stokes方程表述如下：

在三维的情况下，式中：i，j＝ 1，2，3，分别表示笛卡尔坐标系三个方向和为相应方向的平均速度为雷诺应力为平均动压；ρ为流体密度；v 和分别为粘性系数与惯性力平均值。

求解方程式（1）必须首先模拟雷诺应力使方程式封闭，基于各向同性的Boussinesq假设，认为雷诺应力与平均速度梯度成正比，表述如下：

式中：νT为湍流粘度；k 为湍动能；δij为 Kronecker函数。标准的K－ε模型首先由Majumdar和Rodi在1985年用来计算漩涡分离流动，其湍动能和耗散率方程：

式中：vT＝Cuk2／ε。

其他模型参数：C1＝1.44，C2＝1.96，Cu＝0.09，σκ＝1.0，σε＝1.3。

《公路隧道通风设计细则》（JTG／T D70／2—02—2014）规定射流风机理论升压力ΔPfan计算公式：

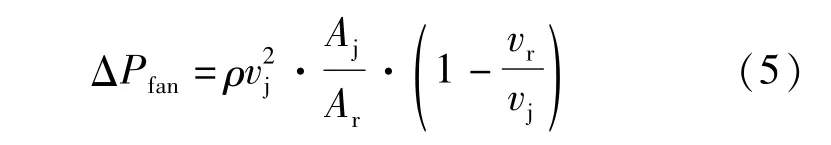
式中：Aj、Ar分别为射流风机出口面积和隧道当量面积；vj、vr分别为射流风机出口风速和隧道风速。

本次数值模拟实际射流风机升压力计算公式为：

式中：P入口为隧道入口处风压；ΔP为隧道沿程阻力损失（包括局部阻力）。

通过对射流风机模型计算得到风流沿横通道和主洞一侧的沿程阻力损失ΔP分别为3.84和0.12 Pa。理论计算结果与实际数值模拟计算结果表明，实际计算升压力值为理论计算值的75%以上。数值计算能够反映实际情况，结果较为可靠。以射流风机布置在横通道为例，横通道升压力理论值和数值模拟计算结果对比见表2。

表2 射流风机升压力计算结果对比

3 射流风机布置优化研究

3.1 工况1结果分析

针对工况1主要讨论射流风机布置在主洞和横通道两种情况，具体如图3所示。情况1为射流风机布置在横通道，以隧道主洞内边缘和横通道的侧壁交点为原点，以横通道出口方向为正方向，与原点距离为5、10、15和20 m的四种位置；情况2为射流风机布置在主洞中，施工横通道中线与隧道外侧壁交点处，以顺时针方向为正方向，与隧道轴线呈60°、75°、105°和 120°的四种安装角度。

为研究射流风机的升压和导流作用，以横通道内的升压力和出口流量为评价指标，压力以流出为正，流量以流出为负。情况1和情况2的风压计算结果以及流量计算结果如图5和图6所示。

图5 工况1压力分布曲线

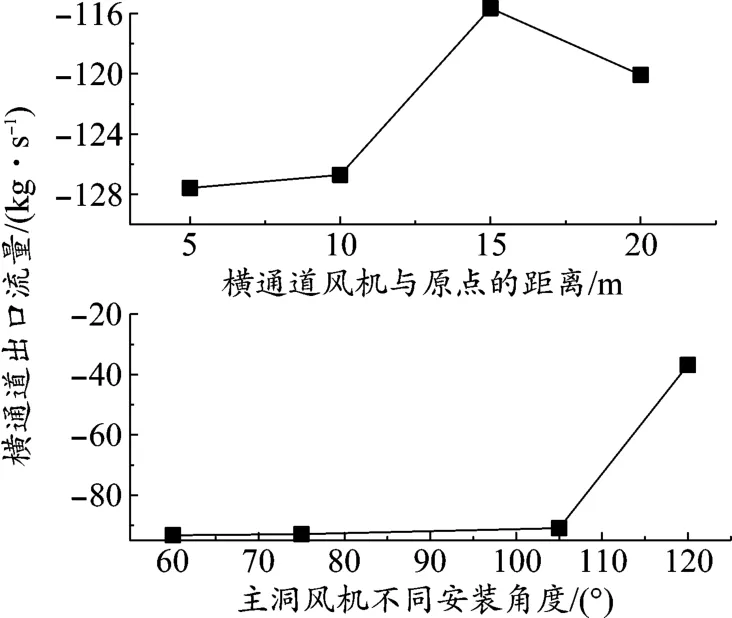
图6 工况1流量变化曲线

由图5可知：随着横通道长度的增加，横通道中风压呈对数型减小趋势，计算出情况1四种布置位置的风机升压力分别为15.54、15.96、14.26和15.2 Pa，在10 m时升压力最大，其值为15.96 Pa，在15 m时升压力最小，其值为14.26 Pa。计算出情况2四种安装角度下的风机升压力分别为7.49、6.71、7.06、5.32 Pa，在60°最大为7.49 Pa，在120°最小为5.32 Pa。

由图6可知：在情况1中随着风机布置位置与原点之间距离增加，横通道出口流量呈先降后升的趋势，在5 m时最大，其值为－127.58 kg／s，在15 m时最小，其值为－115.65 kg／s。在情况2中随着风机安装角度增加，横通道中的流量呈先缓后急的增加趋势，在 60°最大，其值为 －93.32 kg／s，在 120°时最小，其值为 －36.85 kg／s。

3.2 工况2计算结果分析

分射流风机布置在横通道和主洞两种情况讨论，情况1为射流风机布置在横通道中；情况2为射流风机布置在主洞中，与原点距离为15、10、5、0、－5、－10和－15 m七种位置。

工况2取主洞出口1侧的升压力和流量为评价指标。情况1和情况2下的风压计算结果如图7所示，流量计算结果如图8所示。情况2的风压计算结果只取流量较大的一侧制图。

图7 工况2风压分布曲线

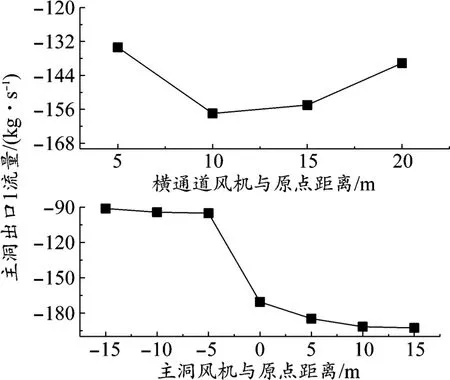
图8 工况2流量变化曲线

由图7可知：在情况1中随着主洞距离的增加，主洞出口1侧的风压呈整体减小趋势，4种布置位置风机升压力为2.03、1.81、1.90和1.41 Pa，在5 m 时最大，其值为2.03 Pa，在20 m最小，其值为1.41 Pa。在情况2中随着主洞距离的增加，主洞出口1侧的风压呈先升后降的趋势，4种布置位置风机升压力为 0.27、0.46、0.47 和 0.48 Pa，在 15 m 时最大，其值为0.48 Pa，0 m时最小，其值为0.27 Pa。

由图8可知：在情况1中随着风机与原点之间距离增加，主洞出口1的流量呈先升后降的“V”型趋势，在10 m时最大，其值为－157.48 kg／s，在5 m时最小，其值为－134.07 kg／s。在情况2中随着风机与原点之间距离增加，主洞出口1的流量呈阶梯型减小趋势，在15 m时最大，其值为－192.58 kg／s，在 －15 m时最小，其值为 －91.25 kg／s。

4 结论

通过对不同风向下施工横通道交叉口处射流风机布置位置和安装角度的综合讨论，得到以下结论：

（1）在风流方向为主洞入、横通道出且风流偏角为60°的条件下（工况1），射流风机布置在横通道时的升压和导流效果优于布置在隧道主洞中。

（2）在风流方向为横通道入、主洞出且风流偏角为60°的条件下（工况2），射流风机布置在横通道时的升压效果优于布置在隧道主洞中，而布置在隧道主洞时的导流效果优于布置在横通道中，此时射流风机的升压效果远低于导流效果。