HPM视角下基于“二重原理”的复数教学设计研究

唐 遥， 易桂生

(江西师范大学 数学与统计学院， 江西 南昌 330022)

1 问题的提出

《普通高中数学课程标准(2017年版2020年修订)》(以下简称《标准》)指出，复数作为一类重要的运算对象，有广泛的应用[1].然而当下一些教师因复数教学内容“简单”，加之考试分值占比小，往往重解题、重练习，轻过程、轻设计.在数学教育立德树人的大环境变革下，当前对复数教学设计的研究主要围绕以下四个方面展开：(1)核心素养，如张筱玮等[2]着眼于核心素养对“数系的扩充和复数的概念”进行教学再设计，吕天玺等[3]基于核心素养以“几何意义”为线索进行了复数教学设计研究；(2)HPM，如王海青[4]基于数学史对“数系的扩充和复数的概念”的教学设计提出思考，尹娟[5]进行了数学史融入复数概念的设计和教学研究；(3)教师学科知识，如从建华等[6]研究了MKT下的“数系的扩充和复数的引入”教学设计，卢建川[7]重构了基于问题驱动的高中复数教学内容并开展教学设计研究；(4)学生认知，如李昌官[8]在布卢姆认知目标的指导下进行了“数系的扩充与复数的概念”教学设计研究，甘经娟[9]研究了高中生关于复数单元的概念表象.

对复数教学设计的现有研究充分肯定了核心素养的价值，认识到数学史对于特定教育内容的指导意义，有重视学生发展的导向，一定程度上贯穿了“教师主导、学生主体”的理念，为教学的实施提供了参考.但是还存在以下问题：在教学内容上多集中在“数系的扩充和复数的引入”部分，而对于复数的其他知识涉及较少，缺少整体性的单元教学设计；在教学原理的指导上相对缺乏，更多的是强调数学知识的本身，教师的教与学生的学及数学知识间的逻辑关系并未充分分析.此外，HPM与核心素养的联系程度不够高.基于此，笔者在HPM的视角下从《标准》和高中数学新教材出发，分析复数教学设计背景，在数学教学“二重原理”理论框架的指导下，探讨复数的单元教学设计.

2 教学设计背景

《标准》是课程的纲领性文件，教材是知识的载体，在教学设计前应明晰.为此，整理《标准》对于复数的教学要求[1]，如表1所示.复数属于“主题三 几何与代数”，是培养学生数学学科核心素养的重要载体.三个版本最新教材中复数的数学史料呈现情况如表2所示.不同版本所呈现的数学史料不乏有相同之处，都有关于复数概念形成的背景，尽管呈现形式不尽相同.北师大版和湘教版还专门设置了阅读材料作为学习内容的补充.

表1 《标准》对于复数内容的相关要求

表2 不同版本新教材中“复数”的HPM内容比较

可见，HPM的渗透是教材编写者的共识，对于复数的教学有一定的指导性.然而，把HPM融入教学绝非易事，其原因主要有：教师要充分储备复数的数学史知识，要对复数概念有完整的理解，要认识受教育者的“最近发展区”等.另外，HPM应用于复数教学时不应简单拼接，应着重揭示含于历史进程中的数学文化价值[10]，体现数学的思想、方法和精神.

3 教学理论基础

数学教育是“数学”与“教育”的双向建构[11]，既有一般教育共有的特征，又有其数学自身的特性.在这种思想基础上，数学教学研究遵循“教与学对应”和“教与数学对应”，数学教学设计从学生的“学”和“数学”的本质上开展.此外，在新课改的背景下，学科核心素养的出台倒逼教学设计的变革，教学设计要从设计一个知识点或课时转变为设计一个大单元[12].因此，数学单元教学设计就显得尤为重要了.

3.1 教与学对应

“教与学对应”原理由认知主义心理学家皮亚杰(Jean Piaget)提出，它源于夸美纽斯(Jan Amos Komensky)的“教育适应自然”思想[13]，即人类的教育活动应以自然界的一般规律为基础，根据人的自然本性和年龄特征，使学习者的智力得到充分的发展.数学教学要从学生出发，教师的“教”要以学生的“学”为基础，教学的设计、实施和评价等也应根据学生的学情来确定.这与布鲁纳(Jerome S. Bruner)的“教的理论以学的理论与发展的理论为基础”[11]也是一致的.

不同的学生对之前接触的数系扩充经验不一致，此外数系扩充经历了漫长的发展过程，学生不可能亲身经历，之前已经获得的间接经验也相对有限.因此，在学生已有认知基础上确定复数教学的重难点显得尤为重要.学生对于数系扩充并不陌生，但是在为何还要将数系扩充至复数这一点上可能会存在理解上的问题.所以在教学设计中要讲清复数概念形成的来龙去脉，并扩充学生的知识面，在引导得出复数的概念之后举例说明它在现实世界中的应用.

3.2 教与数学对应

有理论张力的数学教育学体系的逻辑起点有两个维度：一个维度是教育学，另一个维度是数学教学[14].数学教育是研究数学教学方法与实践的学科，认识数学的学科课程内容在数学教育中的重要价值，这样数学教育才能达到育人目的.数学教学中的“教与数学对应”与“教与学对应”原理相辅相成.

数学对象，如定义、公式、概念、法则等，往往有不同的表现形式，但它本身所固有的根本属性不变.因此，站在“教与数学对应”原理的角度，数学教学不仅要让学生认识形式，如记住公式、符号等，更重要的是使学生把握本质，即理解其在特定范围内始终不变的特质[15].“复数”来源于解方程的现实需要，它在教材中是静态的定义，但从HPM的角度出发更能体会其动态的形成过程.

复数问题的发现始于古希腊时代丢番图(Diophantus)求解一元二次方程，但当时并未被承认；至1545年意大利数学家卡丹(Cardano)在作品《重要的艺术》中意识到求解一元三次方程无法避免虚数问题；直到18世纪末韦塞尔(C. Wessel)给出了复数几何表示，这一概念才开始被人们逐渐接受[16].复数的出现既充满历史的痕迹，又影响了现代科学的发展.数学之内有黎曼(Riemann)和柯西(Cauchy)开始了复变函数研究，将数学的眼界由一维扩展至二维，数学之外有物理学家用其解释波动现象等.

3.3 数学单元教学设计

单元是指一个特定主题下相关教学目标、内容、过程、评价的集合[17]，单元教学设计是对单元教学的整体规划和系统安排[18].数学单元教学设计着眼于提升学生的数学学科核心素养，它是在整体思维的指导下，为了突出数学课程内容的主线和内在联系而统筹、重组和优化教材的内容，并将优化后的内容视为一个相对独立的教学单元，在此基础上对教学单元整体进行循环改进的动态教学设计[19].这也契合《标准》中“优化课程结构，突出主线，精选内容”的理念.“复数”是“主题三 几何与代数”的重要内容之一，可以将其视为一个单元，内容主要包括：数系的扩充与复数的引入；复数的概念；复数的代数形式及其几何意义、复数的运算等.

4 预设教学设计

在数学教育的实践研究上，张奠宙先生提倡“上通数学，下达课堂”，把数学的“学术形态”转化为数学的“教育形态”[20].这一转化需要数学课堂教学实践，需要在教学理论的支撑下进行教学设计、预设教学情形.因此，依据“教与学对应”和“教与数学对应”的原理，认识学生的数学认知水平，理解复数的数学概念本质，从而梳理好教学设计的内容.

4.1 基于学生的认知经历，创设良好的教学情境

学生已经学习过的相关内容和认知经历如表3所示，从一年级至八年级持续“经历”数系的扩充.从自然数扩充到整数，然后扩充到有理数，再扩充到实数，新数系和原数系加法、乘法运算相容，并保持运算律.义务教育阶段并未给学生强调数系扩充的规则和特点.学生只有大概的经验，没有形成完整的认识.

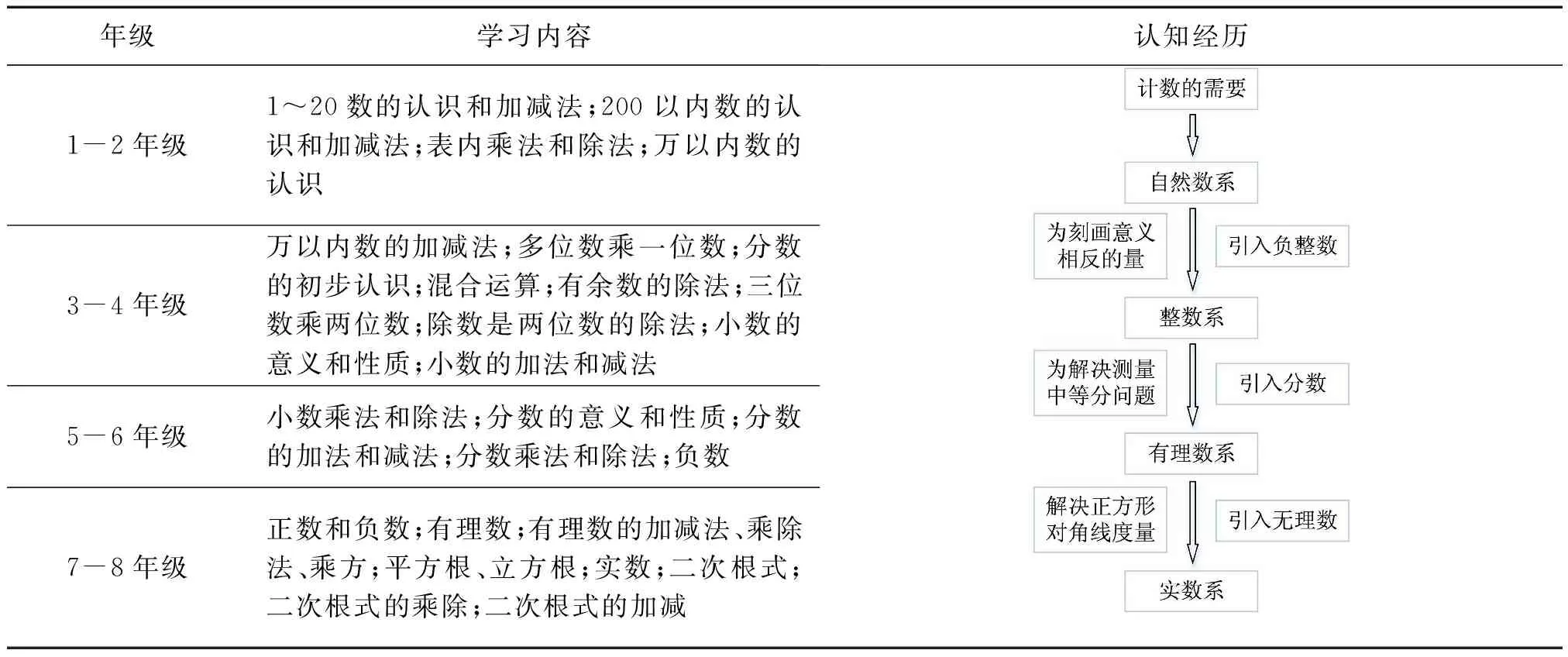
表3 学生已经学习过的相关内容及认知经历

基于上述分析，学生学习复数的认知困难主要有[21]：已经建立的数系扩充经验理性程度不高，特别是对其中蕴含的数学思想方法的理解不够深入；复数是“二维数”，用直角坐标系上的有序数对表示是经验上的一次飞跃.为此，引入复数时可以介绍数学史背景，在解方程中引起认知冲突，在数学情境中激发学生的学习兴趣.

4.2 基于HPM设计数学问题，揭示数学概念的本质

数学问题的设计要合理、自然，基于HPM设计的引导性问题应体现复数的数学逻辑及文化底蕴.在实际教学实践中，教师常采用的引入复数概念的方式有[22]：直接从一元二次方程的求解问题引入；先讲解数系的扩充，然后再从方程求解问题引入；利用卡丹或莱布尼茨的二元二次方程组问题引入；从三次方程求根问题引入.前两种方式遵循复数概念的逻辑顺序，后两种方式则遵循历史顺序.HPM视角下开展教学设计可以将复数的历史顺序和逻辑顺序统一起来.

根据复数发展史，基于HPM的教学设计可用的数学史料、数学抽象出的内容、问题和要点如表4所示.数学史料在数系扩充、复数引入和后续教学中具有引导性，结合《标准》的理念适当选取并有机融合，凸显出教学设计的要点；从解方程中归结出将数系扩充到复数系所要解决的根本问题[21]，为揭示复数的数学本质做准备，并体现出复数产生和发展过程中的科学精神和数学文化.

表4 HPM知识、数学抽象出的问题和教学设计要点

5 教学设计形成

数学学科核心素养体现在四个方面[1]：情境与问题；知识与技能；思维与表达；交流与反思.从这四个方面入手，结合HPM并在数学教学“二重原理”的指导下，尝试将《标准》中复数的考试要求内容“复数的概念”和“复数的意义”进行整合，并适量渗透复数的三角表示，开展单元教学设计.

5.1 教学目标设置

根据上述分析，制定复数单元教学设计的教学目标，如表5所示.将复数的要点进行分解，在知识学习的层次上用“了解”“理解”和“掌握”刻画，同时对应可能涉及的数学学科核心素养.

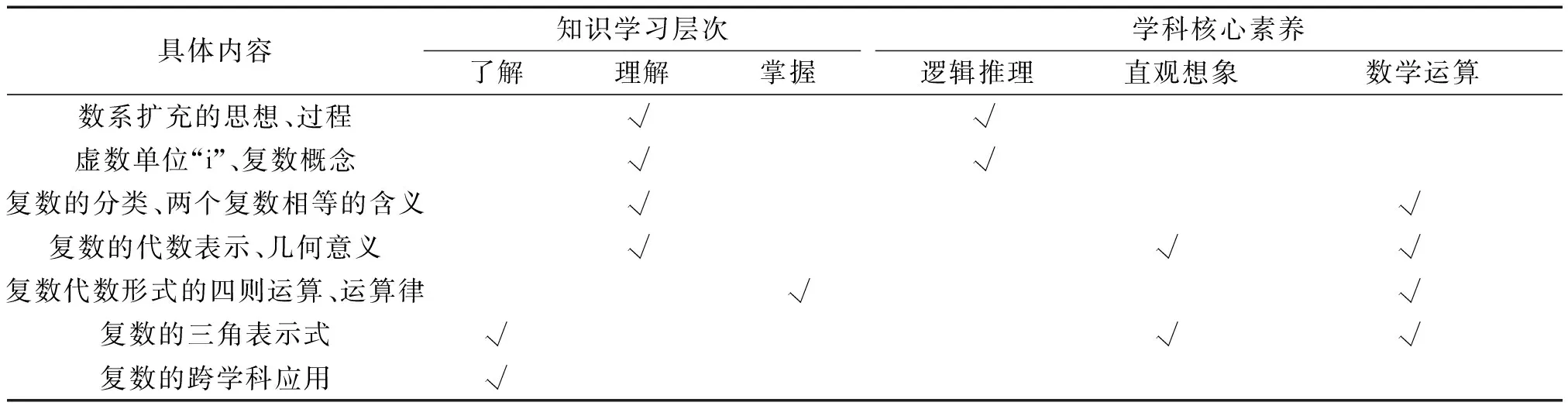
表5 复数的教学目标

5.2 教学重点、难点

教学重点：数系的扩充过程；复数的概念；复数的代数形式及其几何意义；复数的四则运算；复数加、减运算的几何意义.

教学难点：复数的引入；复数的几何意义；复数的三角表示式.

5.3 教学程序设计

【情境与问题】

情境一：1545年，意大利数学家卡丹在著作《大术》中遇到一个问题：将数字10分成两部分，使得它们的乘积为40，则它们分别为多少？

情境二：在16世纪出现了用

(Tartaglia)求解方程x3+px=q.1572年意大利数学家邦贝利研究了三次方程的个例：x3=15x+4.根据上面的求根公式，你觉得邦贝利这个方程有解吗？

问题：当年的数学家们遇到了“实数集不够用”的情况，那么后来又是怎样解决这个问题的呢？

设计意图：通过呈现真实的数学史故事，自然地引出数学问题.结合学生已有的认知水平，给出三次方程求解公式并从数学史中发掘问题，激发学生的学习兴趣，对应了“教与学对应”的原理.

【知识与技能】

经验一：回顾学过的数系扩充过程，体会它来源于生产实践的需要.

(1)远古人类由于计数的需要而创造了自然数，形成自然数系；

(2)为了刻画相反意义的量而引入了负整数，将数系扩充至整数系；

(3)为了解决测量与分配中等分的问题而引入了分数，将数系扩充至有理数系；

(4)第一次数学危机，为了解决正方形对角线测量问题而引入了无理数，将数系扩充至实数系.

经验二：从解方程的角度理解数系的扩充过程[22]，如表6所示，体会它是数学内部发展的需要.

表6 从解方程的角度理解数系的扩充过程

知识建构：引入复数的必要性和数系的扩充.

(1)卡丹二次方程求解.

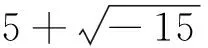
看似合理，实则违反了“负数不可开平方”.

(2)邦贝利三次方程求解.

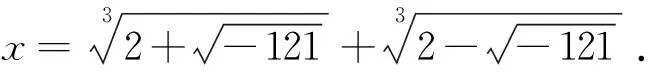
图1 函数f(x)=x3-15x-4的局部图象

(3)学习顿悟.

(4)引入复数系.

设计意图：从生产实践和数学内部需要两个角度回顾数系扩充过程，总结数系扩充过程中遵循的规律和原则，自然地引入复数系，对应“教与数学对应”的原理；数学史和现代教育技术的合理融合，有利于加深学生对数系扩充过程的理解.

知识建构：复数的概念、代数形式、分类及相等的含义.

把扩充后的新数记为a+bi(a,b∈R),通常用z表示，其中a为实部，b为虚部，分别记作：Re(z)=a,Im(z)=b.1813年，高斯首次将这种数取名为“复数”(complex number)，a+bi(a,b∈R)称为复数的代数形式.全体复数组成的集合{a+bi|a,b∈R}称为复数集，记为“C”(大写)，其具体分类如表7所示.在此基础上，引导学生展开讨论，得出两个复数相等的充要条件：实部和虚部分别都相等.由此，再带领学生一起画出数集之间的关系图，如图2所示.

表7 复数的分类

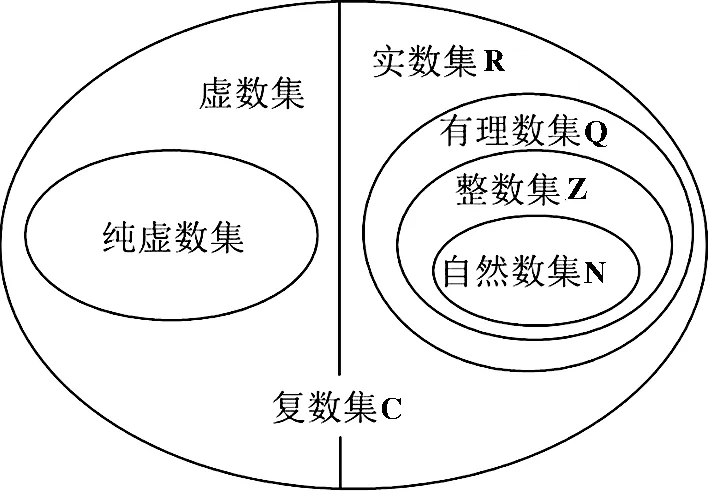
图2 数集之间的关系

设计意图：突出重点，系统传授复数的主要知识，并引导学生明晰数集之间的关系，有利于提升学生归纳总结能力.

知识建构：复数的几何意义.

(1)引出复平面.

复数z=a+bi(a,b∈R)本质上是一对有序数对(a,b).提出问题：复数系是在实数系的基础上扩充而来，实数可以用数轴上的点表示，并一一对应，那么类似地复数能否也用点表示呢？启发学生思考，并展开讨论.有了直角坐标系上的点和有序数对一一对应的经验，复数可以用点表示.但是一维数轴上的点只能表示“一维数”，无法正确地表示复数这种“二维数”.在此基础上，为了表示出复数“二维”的性质，复平面应运而生.介绍复平面的由来：1797年，挪威数学家韦塞尔在著作中首次把全体复数与平面上的点建立了一一对应关系；1831年，德国数学家高斯对复平面作出了详细的说明，至此复平面才被人们广泛地接受，它也被称为高斯平面.

(2)复数的几何意义.

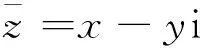
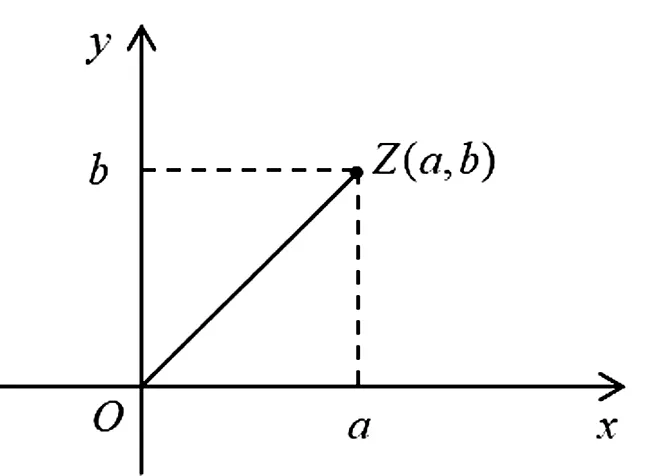
图3 复数z=a+bi的几何表示

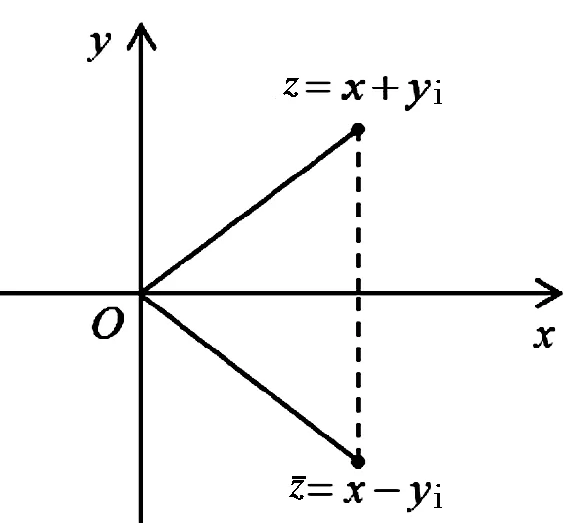
图4 复平面上z和它的共轭复数

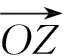
图5 复数z=a+bi的向量形式

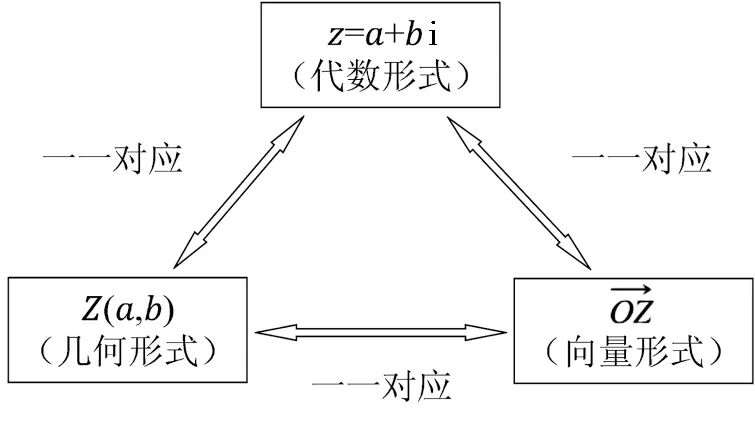
图三者之间的关系

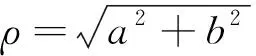
设计意图：通过类比“实数—数轴”，得到“复数—复平面”，实现了一维到二维的联想[24]，从复数的代数形式迁移到复数的几何形式和向量形式，建构了复数的几何意义，并引出了共轭复数、复数模的概念和复数的三角表示，层层递进，中间穿插了复平面的数学史.对应了数学教学的“二重原理”，有利于培养学生数形结合能力及数学运算、直观想象核心素养.

知识建构：复数的四则运算.

(1)复数的加法与减法运算及其几何意义[25].

根据已有的经验，实数的加法满足交换律和结合律，即a,b,c∈R,a+b=b+a,(a+b)+c=a+(b+c).先提出问题：复数的加法应该如何规定，才能符合类似的结合律和交换律？然后给出三个复数：z1=1+2i,z2=1-i,z3=-1+3i,让学生思考并讨论z1+z2与(z1+z2)+z3的值应该等于多少？归纳总结出任意两个复数相加的运算规则：设z1=a+bi,z2=c+di(a,b,c,d∈R)，则z1+z2=(a+bi)+(c+di)=(a+c)+(b+d)i.显然，两个共轭复数的和为实数，即

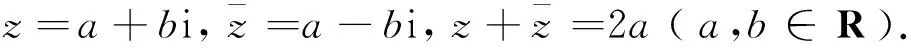
图7 复数加法的几何意义

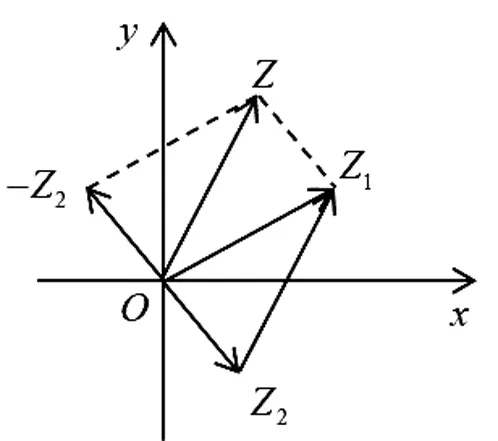
图8 复数减法的几何意义

(2)复数的乘法与除法运算.

实数的乘法对加法满足分配律，如(x1+y1)(x2+y2)=x1x2+x1y2+y1x2+y1y2.设z1=a+bi,z2=c+di(a,b,c,d∈R)是任意两个复数，如何定义它们的乘法法则才可行呢？引导学生探究.为使乘法分配律成立，有：

z1·z2=(a+bi)(c+di)=ac+adi+cbi+bidi;

希望加法满足交换律和结合律，所以有：

z1·z2=ac+adi+cbi+bidi=ac+(ad+bc)i+bdi2.

当b=0,d=0时，复数与实数的乘法法则一致了，说明采用这种办法得到的复数乘法法则与实数乘法法则相容.复数的乘法类似于关于i的“一次二项式乘法”，按照乘法、加法的运算律展开，再合并同类项，结果中如含有i2则替换成-1.

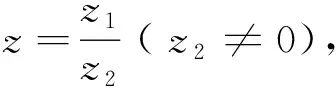
类比根式除法中的“分母有理化”，复数的除法写成分数的形式后，借助除数的共轭复数进行“分母实数化”[21]，再拆开、化简.这里还可以用问题的形式引入，如设实数a,b满足(a+bi)(1+3i)=1,利用方程组求得a,b的值，让学生思考能否用其他方法求解，从而发现并总结复数除法运算的规则.事实上，1837年复数四则运算的法则由爱尔兰数学家哈密尔顿提出，之后他还推广了“四元数”.

设计意图：注重引导学生探究与发现，类比实数推出复数的四则运算法则，既顺应学生的认知又符合数学的发展历程；对于复数的加减法还给出了几何解释，数形结合，有利于培养学生数学运算和逻辑推理核心素养.

【思维与表达】

思维训练：主要通过习题考查学生对复数知识的理解与应用.

(3)已知实数x、y满足(1+i)x=1+yi,求复数z=x+yi的模长.

(4)计算

i÷(1-i).

学习升华：学生根据教师的讲解，反思解题过程中存在的问题，理解其中蕴含的数学思想方法.教师再进行知识拓展，复数在数学之外也“大有作为”，如：达朗贝尔将复变函数论用于流体力学，兰伯特将复数理论用于地图制作等.

设计意图：解题过程中复数知识的灵活应用既训练了学生的逻辑思维，又有利于提高分析问题和解决问题的能力，对应了“教与学对应”的原理.此外，复数跨学科应用的知识拓展，融合了数学史料，使学生认识数学知识的重要性和实用性.

【交流与反思】

提出以下问题：

(1)复数是怎样产生的？复数的概念是什么？

(2)复数的代数表示和几何意义是什么？

(3)怎样理解共轭复数、复数的模？

(4)复数代数表示式的四则运算规则是什么？

(5)复数的三角形式怎样表示？

(6)学习复数后对数学有哪些新的认识与感触？

引导学生系统回顾、交流讨论、归纳总结，并进行学习反思，然后将复数知识之间的联系以及其中的数学思想方法整合[26]，如图9所示.

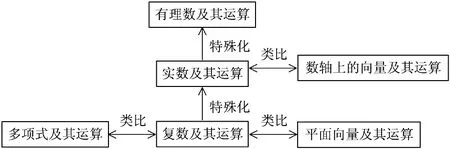
图9 复数知识之间的联系及其思想方法

设计意图：引导学生回顾、梳理所学知识，知识再现、过程再现、交流反思，有利于加深学生对复数的理解，并形成系统的复数知识框架和建构完整的复数认知结构，对应了数学教学的“二重原理”.

6 结束语

数学存在于历史之中, 活的数学存在于活的数学史之中, 活的数学教育讲授的是活的数学和活的数学史[27].HPM视角下将复数的数学史料、数学知识、学生认知有机结合，注重知识的整体性和关联性，把教师的教和学生的学统一起来，使复数的教学变得生动而更加有意义.围绕数学教学的“二重原理”开展复数教学设计，既要考虑学生学习的前后关联和继承，也要凸显数学的本质及其蕴含的思想方法.上述复数的单元教学设计在HPM、“二重原理”理论、数学知识、学生学习等方面的耦合上做了一些安排和思考，以期助力于新课改下围绕数学核心素养的主题式和单元式教学设计研究及实践.