考虑随机生产等待的串行生产系统机会维护建模

宁小涵， 周晓军

(上海交通大学 机械与动力工程学院，上海 200240)

维护是保障生产系统正常运行、提高设备可靠性的有效手段.随着市场需求的日趋多样化，越来越多的制造企业采用面向订单的生产模式.在这一模式下，由于原材料缺乏、需求不足等原因，生产系统常面临着随机的生产等待，进而导致系统整体停机，这也为系统维护带来了机会.为此，如何充分利用随机生产等待以合理优化系统的维护方案，对制造企业降低维护成本、提高生产效率有重要的现实意义.

目前，已有的机会维护研究多围绕如何利用系统中设备强制预防维护所引发的确定性停机时间进行机会维护.Xia等[1]采用单维护时间窗方法判断串行系统中的设备是否接受预先计划的确定性预防维护机会，并对维护活动进行整合优化.俞梦琦等[2]则引入双维护时间窗方法进一步确定维护组合的最佳维护时刻.Zhou等[3]、Zhao等[4]和Nguyen等[5]基于设备的状态判断其是否接受这种确定性机会.Zhou等[6]以最大化短期机会费用节余为目标，采用动态规划求解，判断是否接受强制预防维护引发的机会.显然，已有研究均集中于如何利用设备强制预防维护所引发的系统内部维护机会，没有考虑生产等待带来的外部维护机会，不利于进一步降低维护成本.

在利用外部机会的机会维护研究中，先期有学者针对确定性的外部机会进行研究.Do van等[7]针对多设备串联系统提出新的动态成组维护策略，对预先已知的外部机会进行维护活动规划.Nzukam 等[8]基于Bruss算法选择最优的外部机会对单设备系统进行机会维护.Khatab等[9]考虑利用生产计划中预先已知的生产间歇进行机会维护，提出基于弹性维护力度的串并联系统选择性维护优化模型.随着市场需求的多样化，生产等待的随机性越来越高，为此，Li等[10]提出基于年龄的单设备更换策略，随机生产等待到达时，若设备年龄达到机会更换阈值则对其进行更换.Wu等[11]提出两阶段单设备机会维护策略，第1阶段对设备进行等周期检测，第2阶段利用随机到达的生产等待进行机会维护，以充分利用设备剩余寿命.Yang等[12]采用逆高斯分布来表示设备衰退增量，针对生产等待随机到达的单设备系统，基于状态维护与机会维护相结合的策略，获得预防更换衰退阈值和机会更换衰退阈值.在考虑机会到达随机性的基础上，Truong等[13-14]还考虑机会持续时间的随机性，提出基于时变持续时间阈值的单设备机会维护策略.综合来说，由于随机性导致决策过程复杂，目前对利用随机外部机会进行机会维护的研究多局限于单设备维护规划层面，且没有兼顾系统中其余设备强制预防维护带来的内部机会.

本文以多设备串行生产系统为研究对象，考虑齐次泊松到达且持续时间随机的生产等待，提出一种时间窗与引力窗相结合的维护决策模型，充分利用了生产等待带来的外部维护机会以及系统中设备强制预防维护引发的内部维护机会实施维护优化，以获取系统在维护规划期内的最优维护计划，为面临随机生产等待的串行系统维护决策优化研究提供基础.

1 问题描述及维护策略

串行生产线中的生产等待如图1所示，该生产线由n台设备组成.以串行生产系统为研究对象，在实际生产场景中，该生产线面临随机到达的生产等待且持续时间随机.通常，串行生产系统中任何一台设备的停机往往意味着系统的整体停机，为了减少设备维护造成的停机时间，节约停机成本，可利用生产等待带来的外部机会对生产线进行维护.

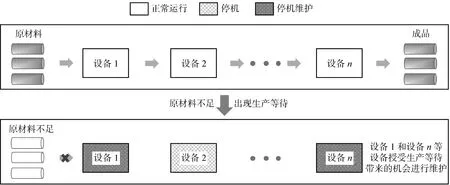
图1 串行生产线中的生产等待Fig.1 Production waits in serial production line

在维护策略方面，对于串行生产系统中的每一台设备，当出现可接受的生产等待时，该设备实施机会维护；若在计划的预防维护周期内没有生产等待被接受，则进行预防维护；设备发生故障时，则进行故障小修.从整个系统的角度考虑，设备的同时维护也意味着系统停机成本的节约，故当某些设备停机进行机会维护或预防维护时，其余设备也存在着提前维护的内部机会.对于由设备强制预防维护(内部机会)引发的维护活动，采用时间窗[1]判断其余设备是否同时维护；而对于由设备接受生产等待(外部机会)引发的维护活动，由于每个设备进行维护的时刻并不固定，传统时间窗无法有效组合这类维护活动，所以引入引力窗判断未接受生产等待机会的设备是否同时维护.

基于以上维护策略，维护建模及决策分为两部分.首先，建立一个随机状态下的设备层维护决策优化模型，分别构建机会维护和预防维护的期望维护成本模型，以最小化各维护周期内各设备期望维修总成本率为目标，获得最优设备时间窗和生产等待持续时间阈值并判断是否接受生产等待的机会；其次，构建综合考虑内部机会和外部机会的系统层维护决策优化模型，以最小化维护规划期内系统维护总成本率为目标，基于系统时间窗与引力窗相结合的维护模型获得系统的最优维护计划.其中，引力窗的定义综合考虑了机会到达时刻与持续时间、设备维护相关成本及机会与设备时间窗之间的关系对于系统层维护整合趋向的影响.

2 维护建模及决策

2.1 考虑随机生产等待的单设备维护建模及决策

考虑到模型的复杂性，首先提出以下假设：① 预防维护与机会维护均为修复非新，且效果相同；② 故障小修仅恢复设备功能不改变其衰退状况；③ 维护活动和生产等待的持续时间相比于维护周期很短，故忽略不记；④ 生产等待到达服从齐次泊松过程，持续时间为已知分布的随机变量[10-13].

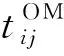
预防维护和机会维护往往不会使设备恢复到全新状态.Pham等[15]概括总结了8种修复非新的建模方法，其中虚拟役龄法在工程实践中应用广泛，故基于该建模思想，采用虚拟役龄描述设备状态，并用虚拟役龄因子θ∈(0,1)表示维护设备健康衰退演化的影响，则第i台设备在第j+1次维护后的虚拟役龄Ai,j+1为

Ai,j+1=Ai,j+θiTi,j+1

(1)

式中：θi为第i台设备的虚拟役龄因子；Ti,j+1为第i台设备第j+1个维护周期的长度.

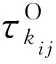
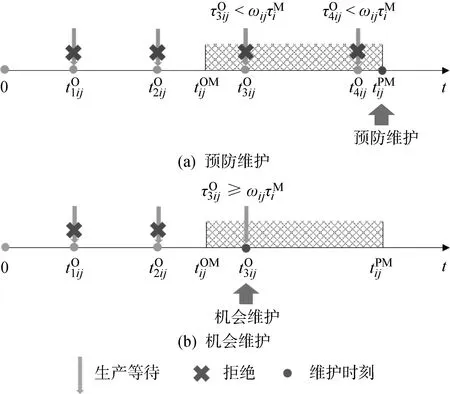
图2 设备维护的两种情况Fig.2 Two situations of equipment maintenance

(2)

预防维护总成本包括维护成本、停机成本和故障小修成本，故第i台设备在第j个维护周期预防维护的期望维修成本率为

(3)

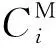
(4)

(5)

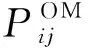
(6)

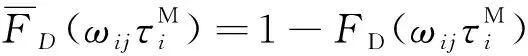
(7)

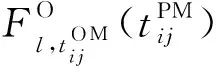
(8)

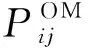
(9)

(10)

(11)

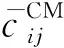
(12)

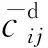
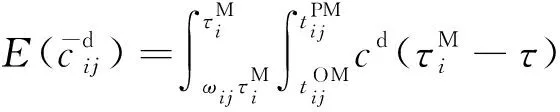
(13)

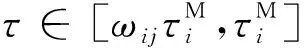
(14)

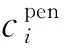
(15)

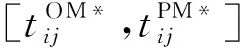
2.2 时间窗与引力窗相结合的系统维护建模及决策

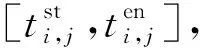
(16)

(17)

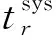
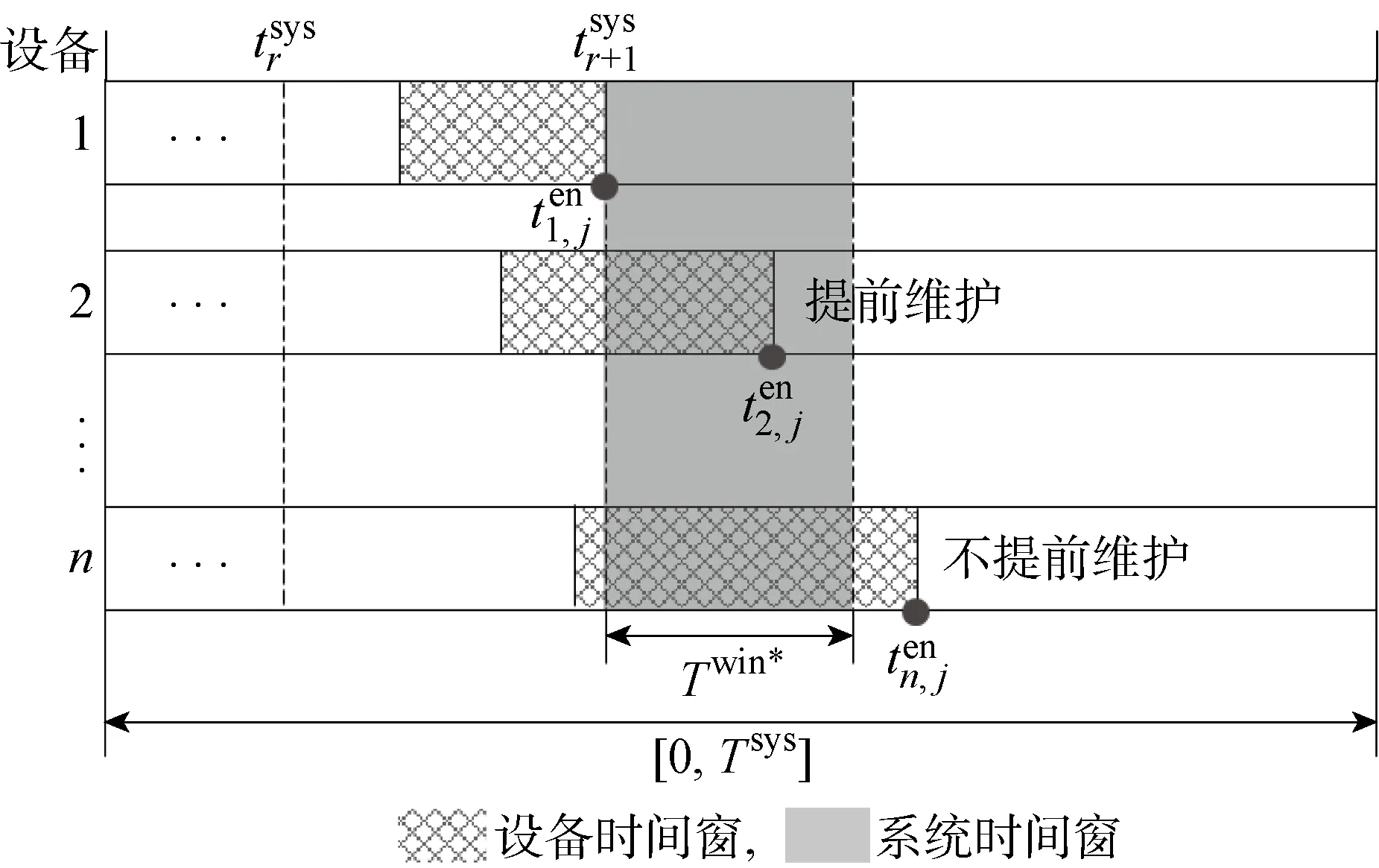
图3 针对强制预防维护的时间窗模型Fig.3 Time window model for mandatory preventive maintenances

而对于外部机会(接受生产等待)引发的系统维护活动，由于每个设备都分别通过设备时间窗判断是否接受生产等待的机会，而不是在一个计划的时间点进行维护，系统时间窗无法处理这类维护活动的优化整合，所以引入引力窗这一概念来进一步对维护活动进行优化整合.

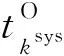
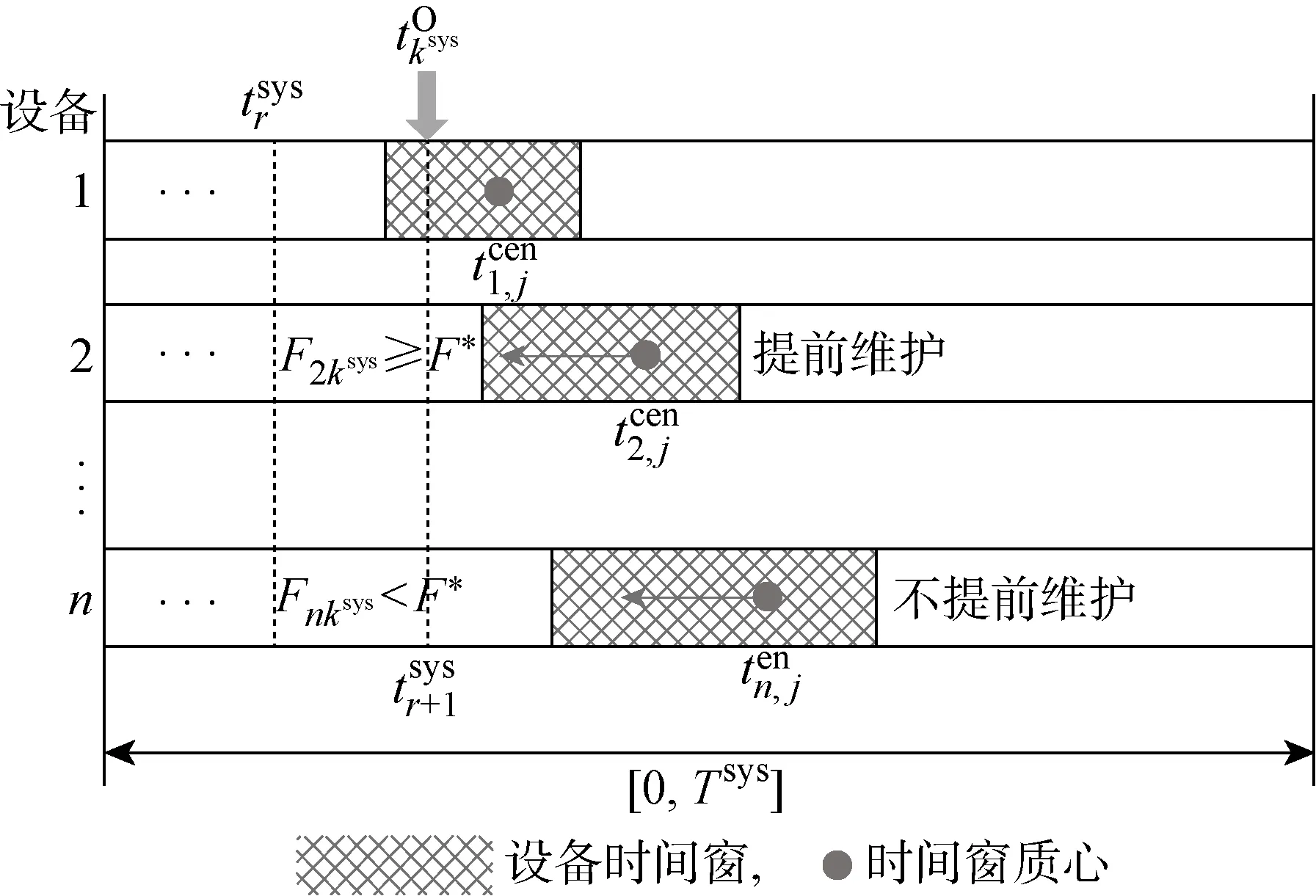
图4 针对随机生产等待的引力窗模型Fig.4 Gravity window model for stochastic production waits

类比于万有引力公式Fiksys可以定义为

(18)

式中：G为引力常量；miksys为机会的“质量”；Mi为第i台设备时间窗的“质量”；Riksys为机会与设备时间窗之间的“距离”.将万有引力公式与机会维护策略相结合的关键在于如何定义以上“质量”和“距离”.引力常量G是一个比例系数，为了计算方便，取为G=1 N·h2/元2；“质量”表示维护整合趋向的大小.机会的持续时间和设备的停机成本影响这一趋向的大小，故机会的“质量”miksys可定义为

(19)

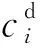
(20)

(21)

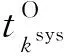
(22)

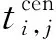
(23)

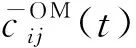
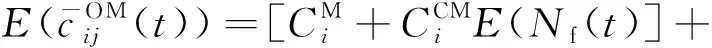
(24)

基于以上所述的系统维护整合模型，具体决策步骤如下.

步骤1从系统初始活动次数，即r=1开始，各设备处于全新状态；

步骤2输入各设备维护时间窗及质心，并赋值给3个时刻tst、ten和tcen，即

步骤3判断累计系统维护活动次数是否达到维护规划期Tsys.若是，结束系统维护规划；否则，转入步骤4；

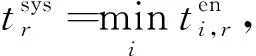
(25)

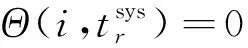
(26)

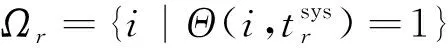
(27)

步骤5进入下一次维护活动，赋值r=r+1，则

(28)

i=1,2,…,n

(29)

i=1,2,…,n

(30)

i=1,2,…,n

然后转回步骤3进行下一次维护活动的维护规划.

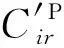
(31)

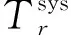
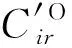
(32)

3 算例分析

3.1 算例概览及策略对比

考虑一个由6台串行设备组成的机械加工生产线，如车床、磨床、铣床等组成的串行生产系统，生产线维护规划期Tsys=1 500 h.Weibull分布特别适用于机械加工设备的故障率建模，故假设该串行生产线中每台设备的故障率分布均服从Weibull分布，即为

(33)

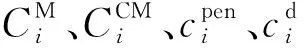
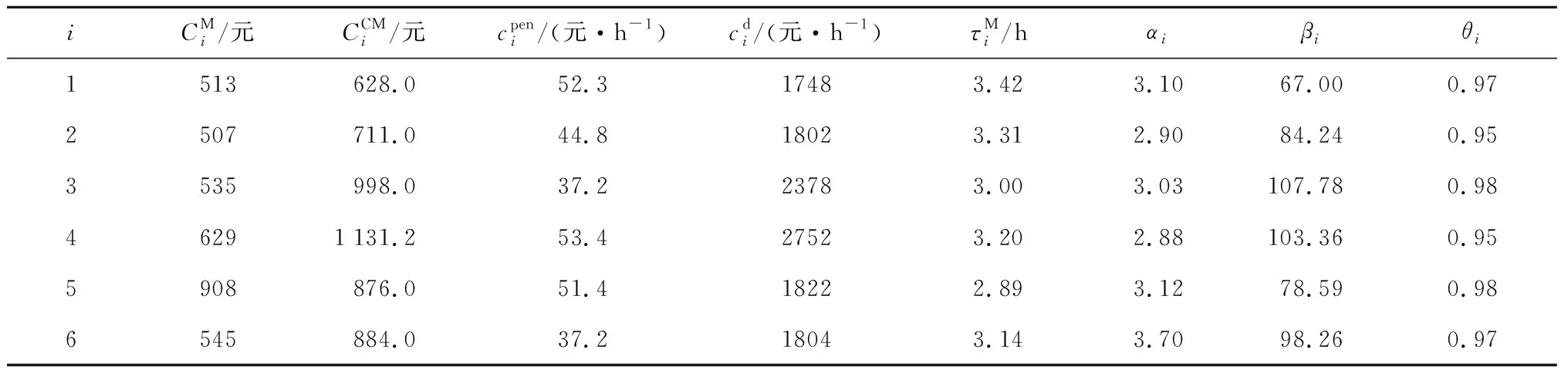
表1 设备参数Tab.1 Equipment parameters

为获得时间窗和引力窗维护整合模型下系统的最优维护策略，基于MATLAB对系统进行仿真，系统维护模型的决策变量为Twin*和F*.Twin*取值以设备预防维护周期为依据，通过设备层的数值模拟得到系统中设备的最长预防维护周期约为250 h，因此Twin*的搜索范围为[0,250] h，搜索步长为10 h，通过仿真得到F*的最优取值落在[3,9] kN区间内，即为搜索范围，搜索步长为0.1 kN.生产等待的随机性给系统带来了不确定性，因此利用仿真获得系统平均总维护成本率，每次数值模拟均对系统做 2 000 次随机场景中的仿真.

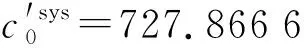
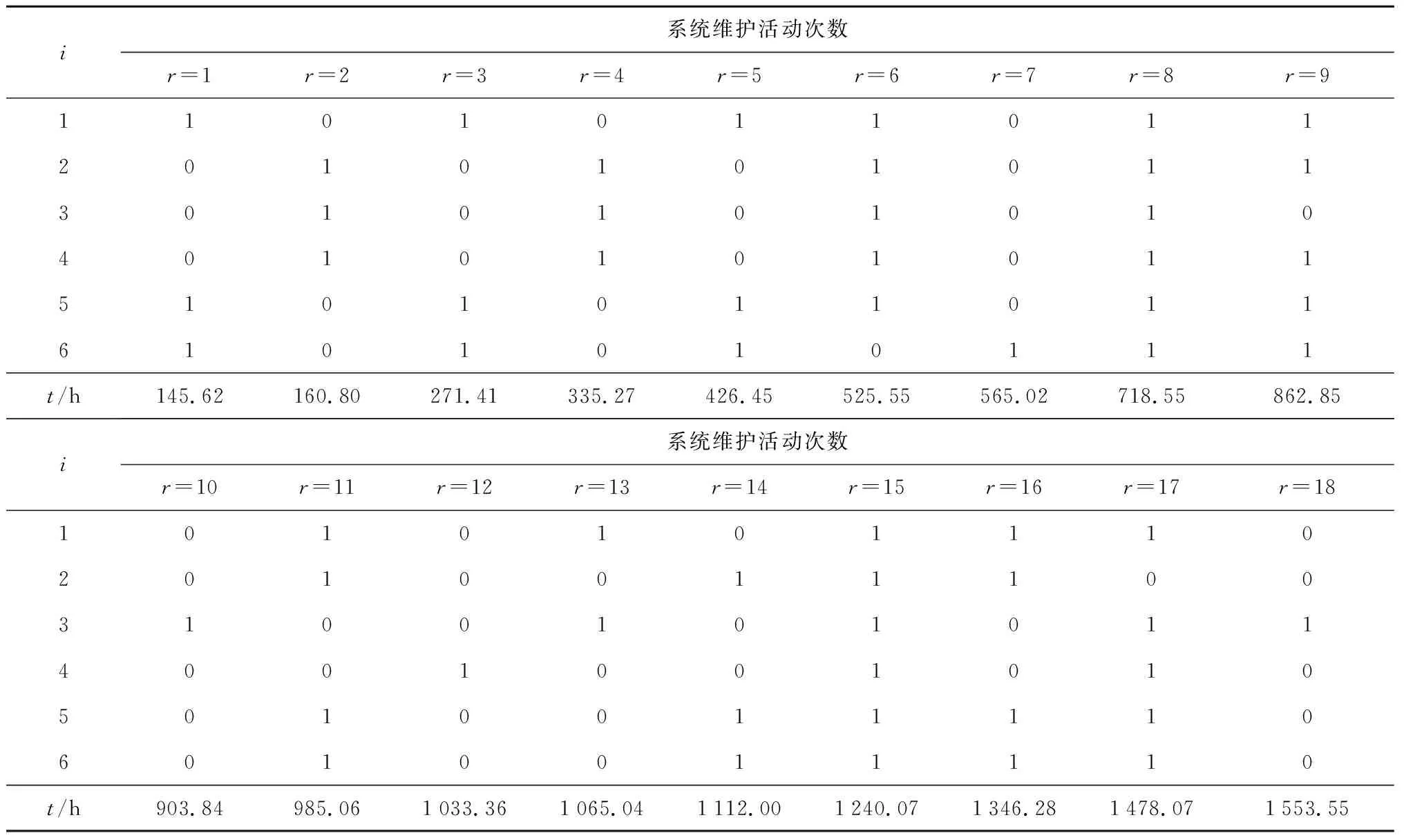
表2 系统维护时刻表Tab.2 System maintenance schedule

3.2 不同停机成本下的策略对比

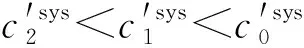
图5 不同停机成本下的系统维护总成本率分析Fig.5 Total cost rate analysis of system maintenances at different downtime costs

(34)

随着停机成本的增加，φ的变化如图6所示.由图6可知，停机成本越大，φ越大，意味着引力窗改进的效果越明显.这是因为当停机成本增加时，设备更趋向于利用生产等待进行机会维护，从而避免设备强制性预防维护导致巨额停机成本的情况.由仿真结果可知，当κ=0.1时，最优维护策略下，在维护规划期内由外部机会引发的系统维护的平均次数为10.152 5次，由内部机会引发的系统维护的平均次数为6.928次；而当κ=50时，最优维护策略下，由外部机会引发的系统维护的平均次数为7.826次，由内部机会引发的系统维护的平均次数仅为0.015次.故停机成本越大时，引力窗对于系统维护计划的改进越为重要；停机成本相对较小时，时间窗对于系统维护计划的改进越为重要.不同停机成本下的具体仿真及优化结果如表3所示.

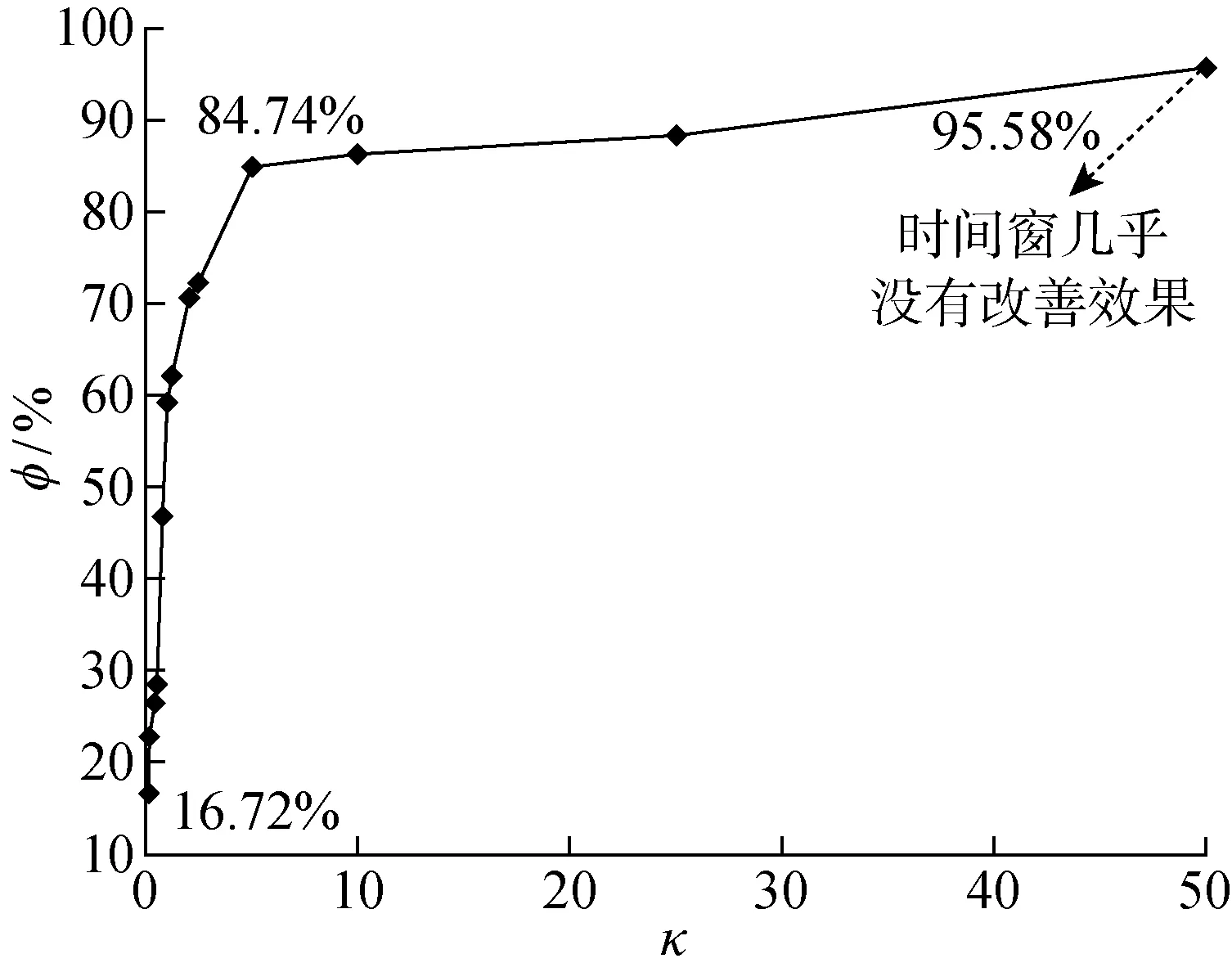
图6 不同停机成本下的引力窗改善占比分析Fig.6 Analysis of the proportion of gravity window improvements at different downtime costs

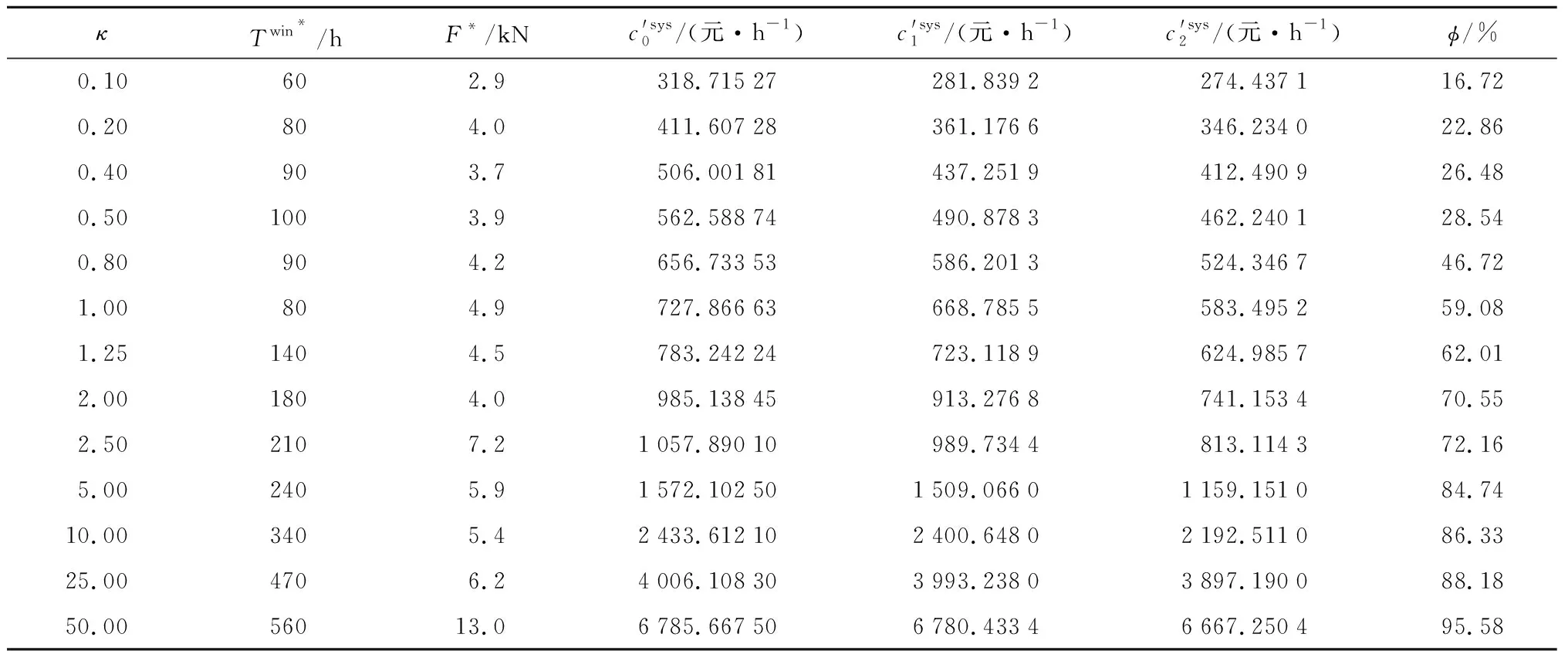
表3 不同停机成本的仿真结果Tab.3 Simulation results of different downtime costs

3.3 不同生产等待到达频率的策略对比

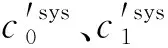
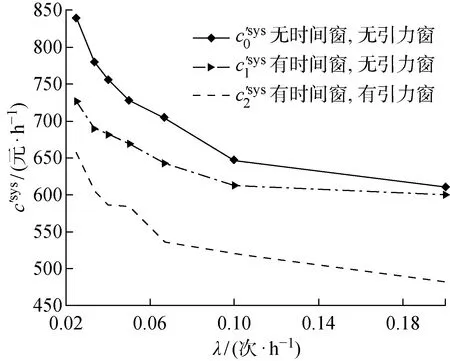
图7 不同生产等待到达频率下的系统维护总成本率分析Fig.7 Total cost rate analysis of system maintenances at different production wait frequencies

此外，随着λ的增大，φ的变化如图8所示.由图8可知，λ越大，φ越大，意味着生产等待的到达越频繁，引力窗改进的效果越明显.这是因为生产等待的到达越频繁，设备越大概率地利用生产等待进行机会维护.由仿真结果可知，当λ=0.025 次/h时，在维护规划期内由外部机会引发的系统维护的平均次数为7.462次，由内部机会引发的系统维护的平均次数为 1.730 5 次；而当λ=0.2 次/h时，由外部机会引发的系统维护的平均次数为14.082次，由内部机会引发的系统维护的平均次数仅为 0.045 5 次.故生产等待的到达越频繁，引力窗对于系统维护总成本率的改进越为重要；生产等待到达相对稀疏时，时间窗对于系统维护总成本率的改进越为重要.不同生产等待到达的频率下的具体仿真及优化结果如表4所示.

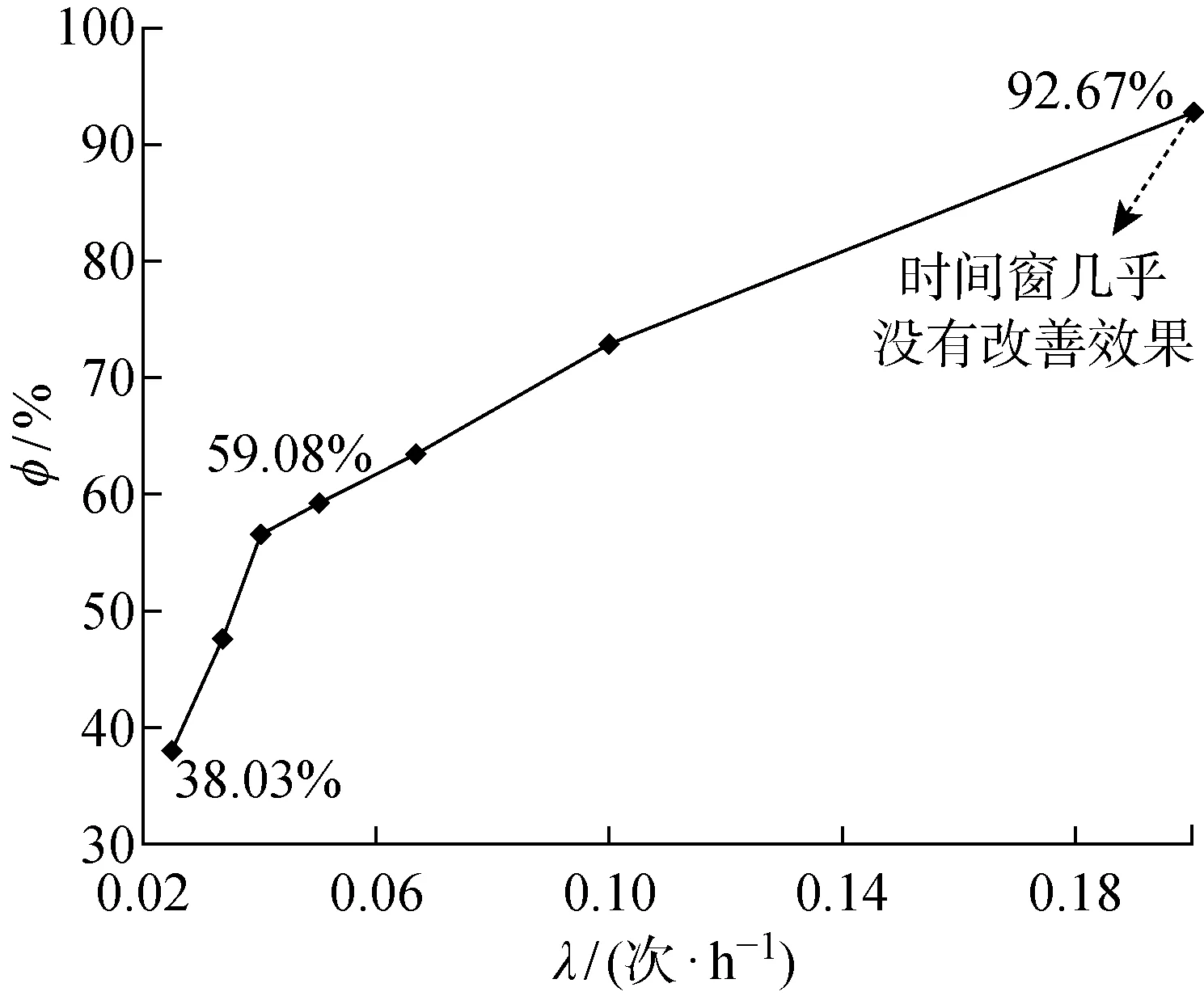
图8 不同生产等待到达频率下的引力窗改善占比分析Fig.8 Analysis of the proportion of gravity window improvements at different production wait frequencies

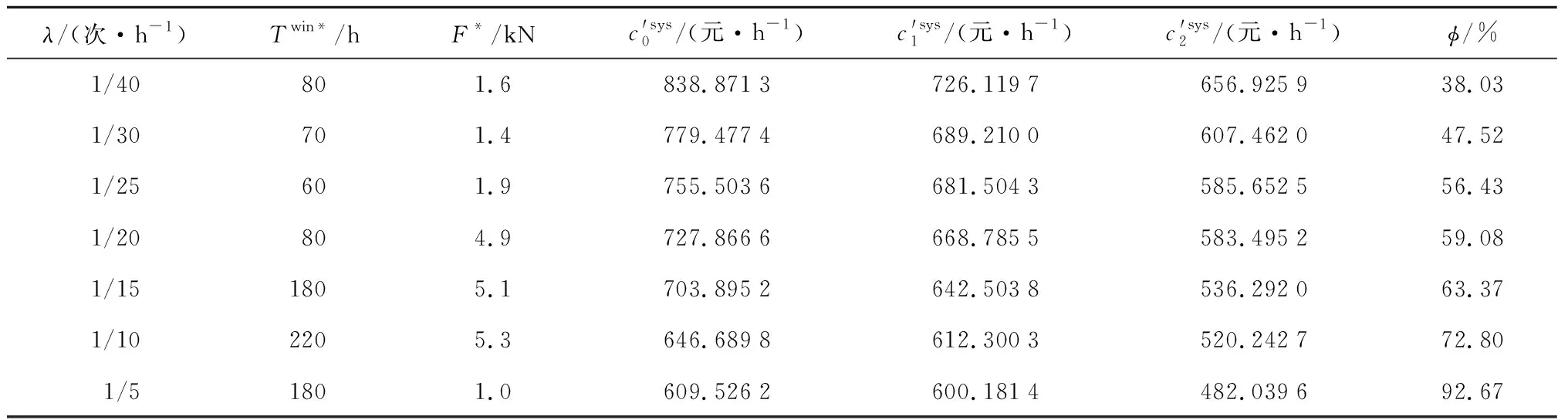
表4 不同生产等待到达频率的仿真结果Tab.4 Simulation results of different production wait frequencies

4 结语

本文同时考虑了串行生产系统面临的由预防维护引发的内部维护机会以及由生产等待带来的随机外部维护机会，提出时间窗与引力窗相结合的机会维护策略.对设备和系统分别进行维护建模，利用时间窗对内部机会引发的维护活动进行整合，利用引力窗对外部机会引发的维护活动进行整合.算例分析结果表明，在复杂的参数环境中，相对于无维护整合模型和时间窗模型，时间窗与引力窗相结合的决策模型均可以获得更低的系统维护总成本率，具有广泛的适应性与稳定性，且随着停机成本的增大或生产等待到达频率的提高，引力窗的改善占比呈递增趋势.因此，在停机成本较高或生产中断频繁发生的串行生产系统中，引力窗对于维护计划的改进更为重要.