基于在线改进符号序列熵与逻辑回归模型的岸桥起升减速箱在线退化评估

2021-11-05孙德建

上海交通大学学报 2021年10期

王微, 王冰, 胡雄, 孙德建

(上海海事大学物流工程学院，上海 201306)

岸桥是一种对集装箱进行装卸的大型港口起重设备.起升机构是岸桥最重要的工作机构，主要实现集装箱或吊具的升降运动，一般由驱动电机、减速箱、卷筒以及钢丝绳等设备组成.岸桥运行环境恶劣且工况特殊，在高速、重载、大冲击的周期性集装箱吊装作业中，起升减速箱会承受由强烈动载引起的振动冲击，长期作用下会诱发性能退化甚至突发故障[1]，导致停工停产甚至是人员伤亡.目前，起升减速箱已成为岸桥设备管理中的易损部件和安全薄弱环节.如果能够在线监测其状态信号，跟踪其性能退化趋势，在线识别其性能退化状态，就能有效开展基于状态的维修，提升岸桥的安全可靠性.

特征提取是基于状态维修(CBM)中的关键步骤[2].特征提取的目标是在监测信号中挖掘能够反映性能退化趋势的定量指标.目前，应用较多的方法以时域、频域以及时频域分析等线性方法为主[3-5]，提出了基于均方根(RMS)谱[6]、峭度[7]、谱峭度[8]等性能退化指标.考虑到机械振动信号的非线性、非平稳特性，近年来基于信息熵与分形的复杂性分析方法开始应用到轴承、齿轮等旋转机械的退化规律分析中.文献[9]提出用时频熵指标来度量轴承振动信号的复杂度并反映其退化过程.文献[10] 提取轴承振动信号的多尺度模糊熵(FE)和变分模态分解(VMD)能谱熵作为退化特征向量，利用全寿命数据样本的退化特征向量训练不同退化状态下的隐马尔科夫模型(HMM)，最后通过建立的HMM模型库并根据最大对数似然概率原则识别轴承退化状态.除此之外，还包括多元多尺度熵[11]、多尺度置换熵[12]等退化特征.

前期研究表明，监测得到的起升减速箱振动信号中包括了大量的随机冲击成分，直接影响了信息熵和分形维数的精确化计算，使得结果波动性强，无法准确反映信号内部的复杂性规律.而符号动力学分析能够采用符号化的方法处理时间序列，保留前后幅值变化，忽略幅值大小，是一种“粗粒化”的信号处理方式[13].以该理论为基础的符号序列熵(SSE)起源并主要应用于脑电信号分析中[14-16]，能够刻画符号序列中的信息熵演化规律，具有计算简便、运算速度快、抗干扰能力强的优点.目前，该算法很少应用在设备特征分析的研究中.考虑到减速箱现场振动信号随机冲击大的特点，以符号序列熵为基础分析退化进程中的复杂性规律是可行的.

为了解决岸桥起升减速箱的健康状态在线评估问题，本文研究并提出基于改进符号序列熵(ISSE)-逻辑回归模型的退化状态在线评估方法.引入阈值因子对符号序列熵进行改进，以逻辑回归模型[17]为基础，对训练样本进行模型重构，计算未知状态样本的模型偏移量，并以此评估机械设备的健康状态.以起升减速箱全寿命振动监测信号进行方法的有效性验证，本文开展的研究能够有效解决起升减速箱退化状态评估关键技术问题，为港口起重机械领域同类问题研究提供借鉴，推动港口起重机械的故障预测与健康管理(PHM)实践.

1 符号序列熵及其改进

1.1 符号序列熵

符号序列熵应用在脑电信号分析中，计算方法如下[18].

假设R是长度为B的脑电信号，该信号的电位变化是非平稳的随机信号.对信号进行符号化处理，以0、1、2这3种符号保留脑电信号的变化方向信息，则有：

(1)

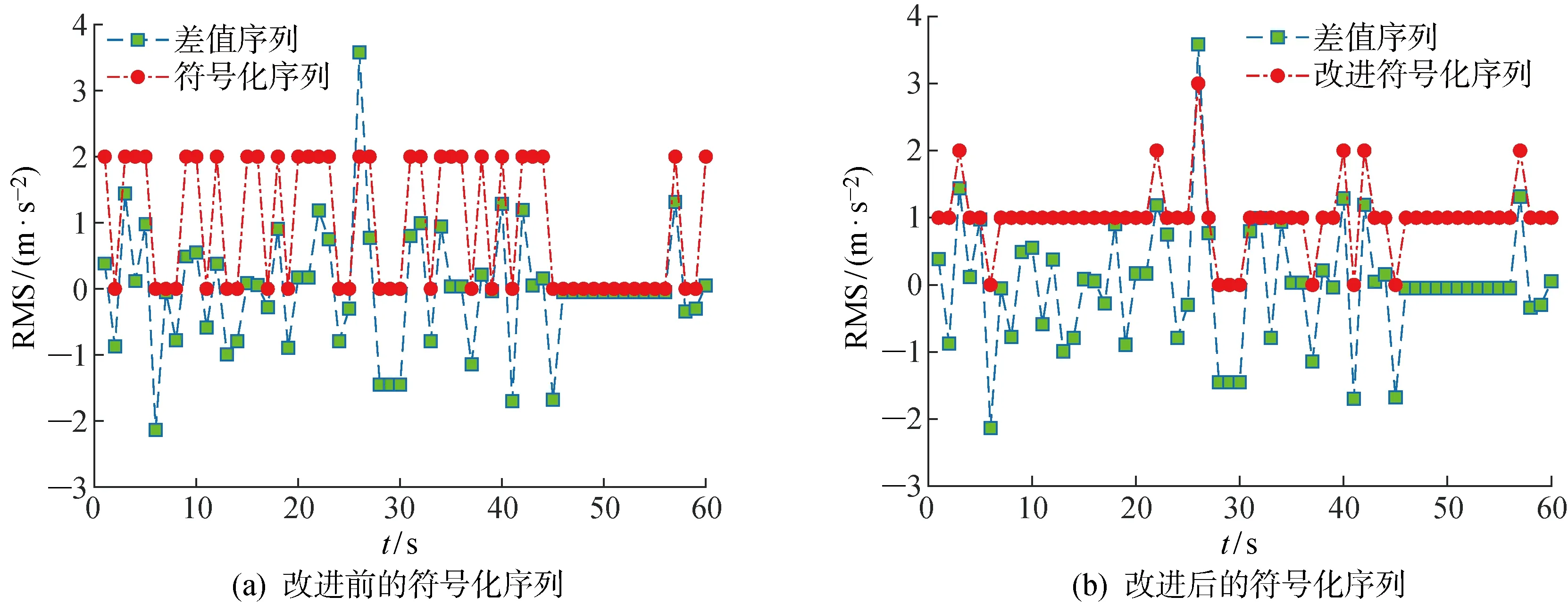
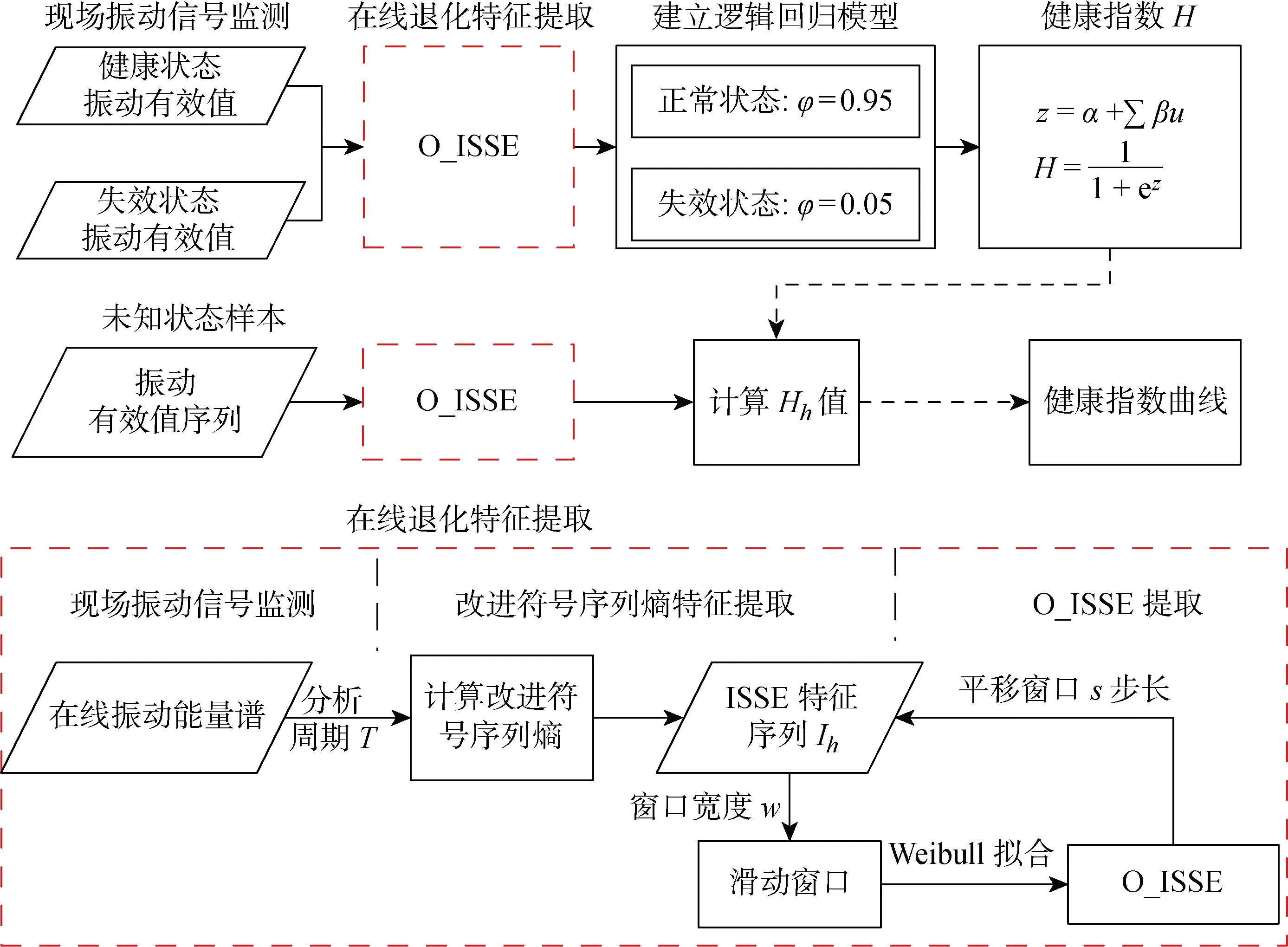
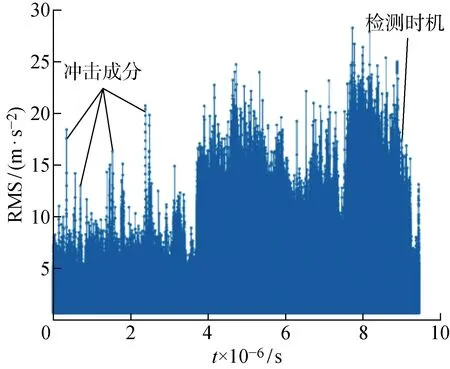
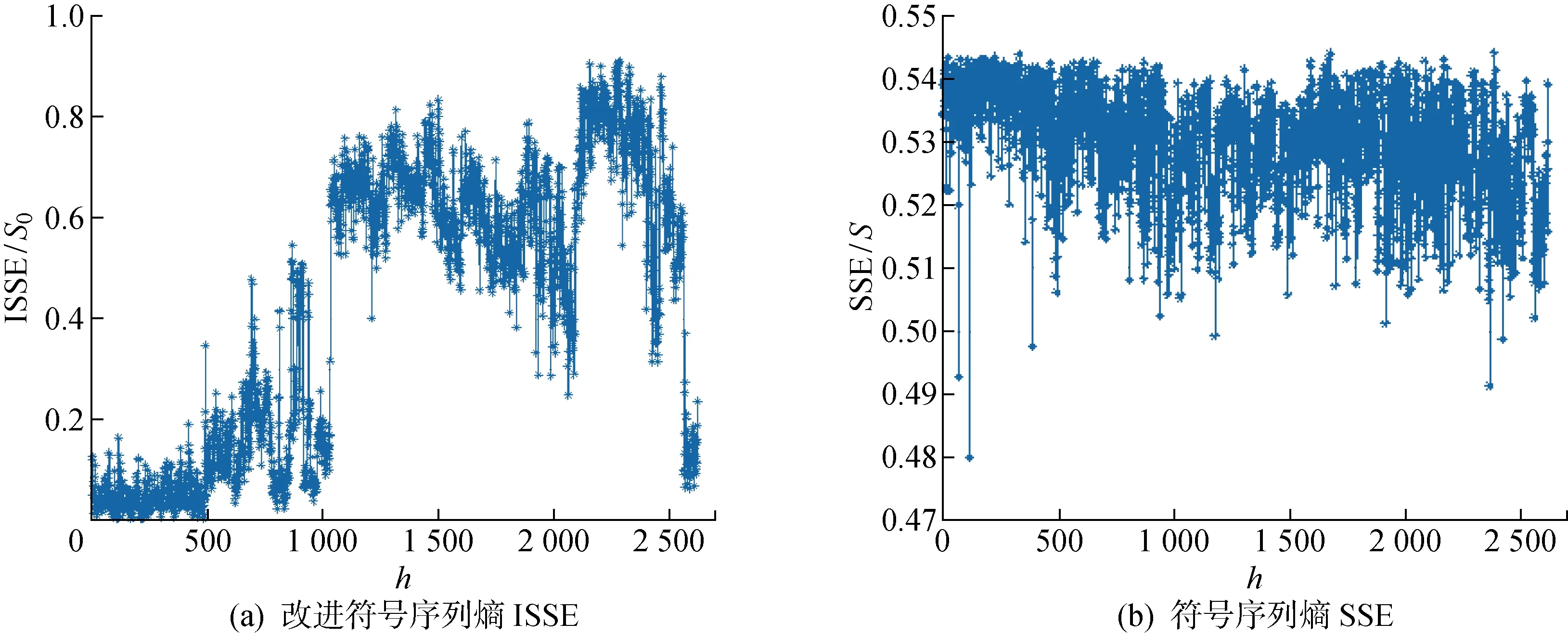
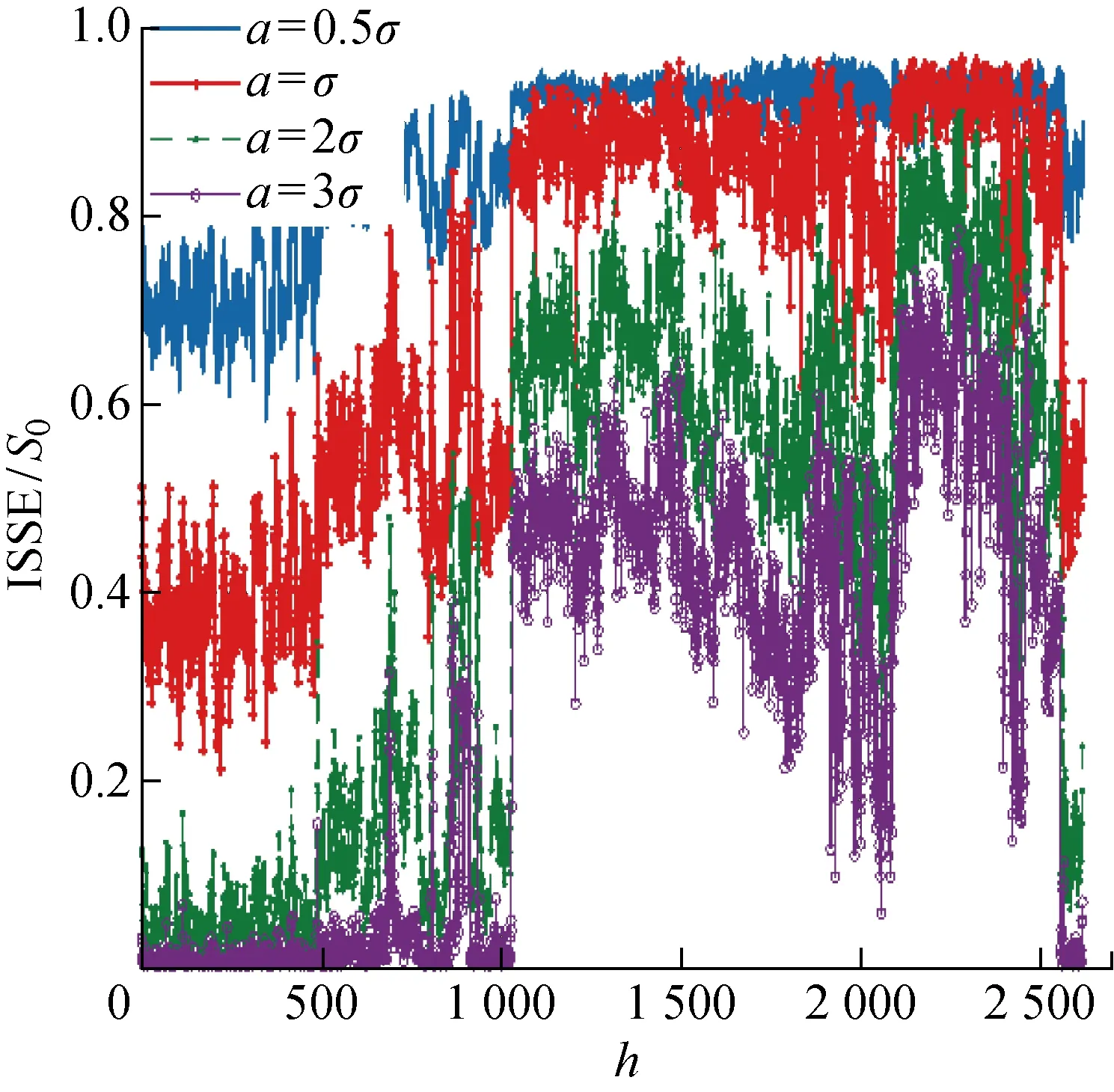
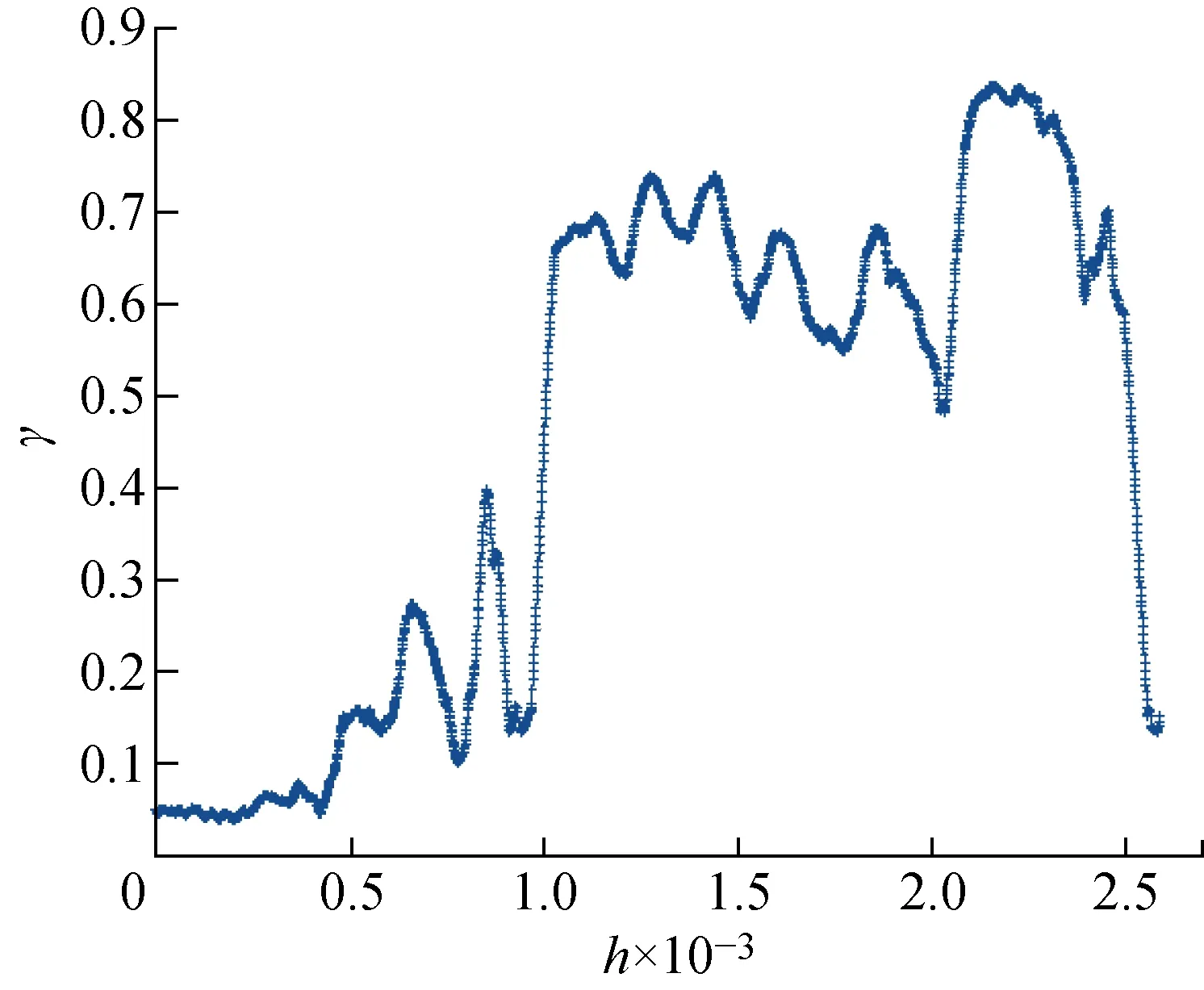
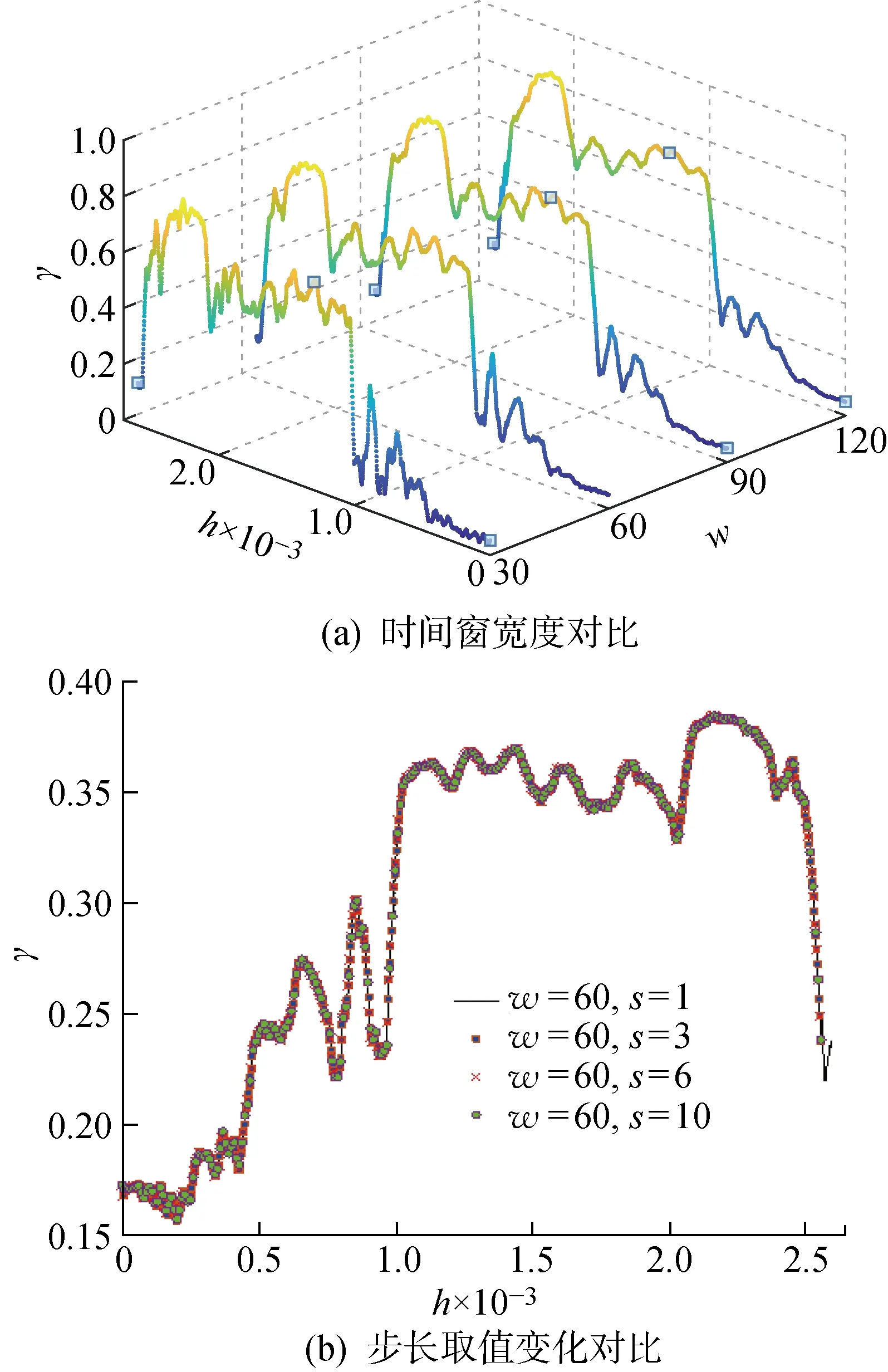
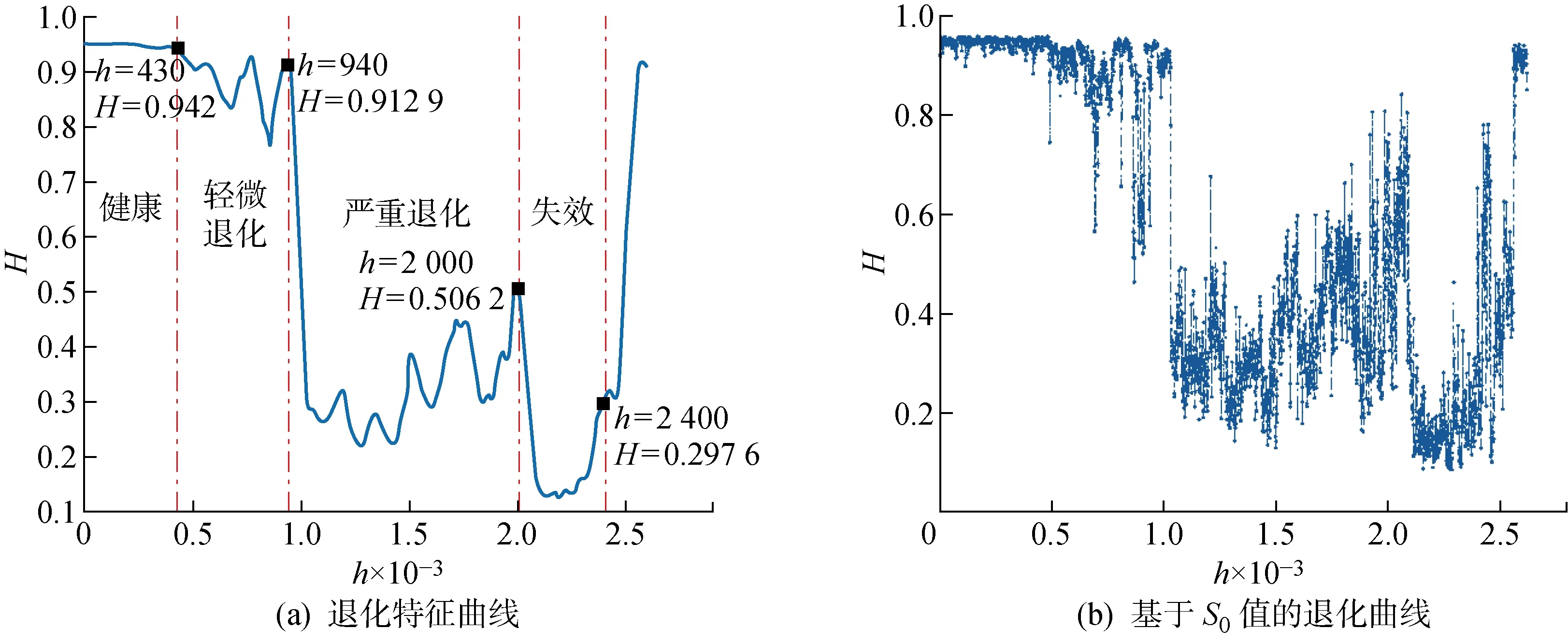
以滑动窗方法构造长度为m的向量Xi.Xi中可能的符号模式共包括M=3m种，则有：

Xi=[xixi+1…xi+(m-1)]

(2)

i=1, 2,…,B-m

统计Xi中每种模式出现的概率，以Nj为出现第j个符号模式的次数，Pj为出现第j个符号模式的概率，则有：

(3)

j=1, 2, …,M

按照下式计算归一化的符号序列熵：

(4)

式中：m的取值无特殊要求，一般N>3m即可.

1.2 改进符号序列熵

符号序列熵算法以相邻点的信号幅值大小确定序列符号，以符号1、2、3灵敏地反映信号的变化方向信息.但岸桥现场监测信号中包括较多的噪声和随机冲击，极易影响符号序列熵的取值，为了提高算法的稳定性，同时挖掘信号内部定量的复杂度大小，引入阈值因子a，在保留方向变化信息的同时，增加了“粗粒化”的幅值变化信息.以阈值因子a划分方向变化的幅值区间，并采用1、2、3、4、5进行符号化处理，具体计算如下：

(5)

阈值因子a决定了幅值区间划分的“粗粒化”程度.一般认为，当设备处于稳定的健康状态时，其符号化模式是稳定的.同时，由于标准偏差能够衡量数据分布的分散程度，所以本文将阈值因子a设置为健康状态信号标准偏差的2倍，按照式(5)的符号化规则，健康状态的信号具有稳定的符号化模式.

以一组起升减速箱振动有效值序列为例.假设a=1，算法改进前后的符号化处理效果如图1所示.其中：t为时间；RMS为均方根.由图1可知，通过引入阈值因子，差值序列的幅值在 |a| 之内的采样点均被符号化为2，并且保留了差值序列的幅值信息，降低了原算法对于方向变化的敏感性，使得改进后的符号模式变化更加稳定，从而体现出信号内部的整体模式变化规律.

图1 序列符号化改进前后对比Fig.1 Comparison of sequence symbolization before and after improvements

在对符号化过程进行改进后，按照式(2)和(3)进行向量构造和模式统计，计算得到的改进符号化序列熵如下：

(6)

2 基于在线改进符号序列熵与逻辑回归的在线退化状态识别

以改进的符号序列熵、Weibull分布[19]、逻辑回归模型为基础，提出基于改进符号序列熵与逻辑回归的在线退化状态识别方法.首先结合ISSE和滑动窗Weibull分布，提出在线改进符号序列熵(O_ISSE)的计算方法，之后结合逻辑回归建模，实现退化状态的在线识别.该方法的流程如图2所示.其中：Ih为第h组ISSE特征序列；Hh为第h组的健康指数；w为窗口宽度；z为回归模型；s为平移窗口步长；α为模型的常数项；β为模型的系数；u为前一环节特征提取所得到的O_ISSE；φ为训练样本的状态阈值；T为分析周期；H为健康指数.

图2 在线退化状态识别流程Fig.2 Process of online degradation status recognition

由图2可知，在线退化状态识别主要包括以下几个关键步骤.

(1) 现场振动信号在线监测.以在线监测采集系统为平台，持续获取振动监测信号.考虑到机械大数据的海量性以及低密度，本文采用的是岸桥现场监测得到的振动有效值序列yi(i=1, 2,…,n).

(2) ISSE特征提取.设置分析周期T，将振动有效值序列划分为分析组Gh(h=1, 2,…, floor(n/T)).其中，floor函数代表取下整数.划分方式如下：

G1={y1,y2,…,yT}
G2={yT+1,yT+2,…,y2T}
⋮
GJ={y(J-1)T+1,y(J-1)T+2,…,yJT}

(7)

计算阈值因子a，分别计算每个分析组Gh(h=1, 2,…, floor(n/T))的ISSE特征，得到ISSE特征序列Ih.

(3) O_ISSE计算.按照滑动窗方法，设置每个滑动窗口宽度与平移窗口步长，得到一组滑动窗口Wq(q=1, 2,…, floor(n/T)-w+1)，滑动窗口宽度即代表每个滑动窗口包括w个ISSE特征序列.划分方式如下：

W1={I1,I2,…,Iw}
W2={I1+s,I2+s,…,Is+w}
W3={I1+2s,I2+2s,…,I2s+w}
⋮
WQ={I1+(Q-1)s,I2+(Q-1)s,…,I(Q-1)s+w}

(8)

分别对每个滑动窗口内的ISSE序列进行Weibull拟合，计算得到该分布的尺度参数，以此作为在线退化特征O_ISSE.计算完毕后平移窗口s步长，在线得到O_ISSE在线退化特征序列.

(4) 逻辑回归模型训练.选取典型的健康和失效状态样本作为数据基础，设计基于逻辑回归模型的健康指数H.定义健康状态样本的健康因子H=0.95，失效状态样本H=0.05.训练逻辑回归模型，得到参数α、β取值.建立逻辑回归模型，如下式所示：

z=α+∑βu

(9)

(5) 退化状态识别.按照流程提取未知状态样本的在线退化特征，输入至逻辑回归模型，计算得到样本的H值，判断设备当前性能的退化状态.

3 起升减速箱实例分析

3.1 起升减速箱全寿命数据集

采用起升减速箱全寿命数据对提出的方法进行验证.全寿命数据来自上海港某集装箱码头的岸桥起升机构减速箱.自该岸桥列装以来，课题组NetCMAS系统一直对该设备40多个关键测点的振动、温度、应力信号进行在线监测[20]，现场数据监测示意图如图3所示.岸桥不同测点部位安装振动、温度传感器以及应变片，通过电缆连接至岸桥现场采集处理主机中，实现数据的在线监测与存储.

图3 数据监测与测点采集Fig.3 Data monitoring and measurement points

持续监测近7年8个月后，系统报警.经停机检修后发现，失效位置为减速箱高速输入轴滚子轴承，失效形式为滚子磨损.现场检修图如图4所示.

图4 减速箱轴承失效现场检修图Fig.4 On-site inspection of gearbox bearing failure

本文所采用的全寿命数据集来自起升机构减速箱高速输入轴垂直方向振动传感器.采样频率为24 kHz，采样时间为1 s，采样间隔为10 s，每采样1次，系统自动计算该采样时段有效值RMS，在线获取该测点的振动RMS序列.通过系统自动预处理，该数据集中停机等非工作态的振动有效值序列被滤除，得到全寿命数据集的时域波形如图5所示.由图5可知，从整体上看，该测点的振动有效值在不断增大，同时包括了许多冲击成分，这些都是由集装箱吊装作业时的瞬间启停造成的.单纯通过有效值很难精确跟踪性能退化状态，随机冲击的存在很可能造成误判，有必要进行进一步的退化特征提取.

图5 振动有效值序列时域波形Fig.5 Time domain waveform of vibration effective value sequence

3.2 ISSE退化特征提取

设置分析周期T=3 600 s，起升减速箱全寿命数据集共划分为 2 622 组Gh(h=1, 2,…, 2 622).分别计算每个分析组的改进符号序列熵ISSE，阈值因子a设置为G1标准偏差SD的2倍，即a=2SD(G1)，其中G1={y1,y2,…,yT}.

起升减速箱全寿命演化进程中的ISSE特征序列Ih如图6(a)所示.退化程度越深，ISSE取值呈现逐渐增大的趋势，并且具有明显的阶段性.由于振动有效值序列中较强的随机冲击，使得ISSE特征曲线中仍存在明显的随机波动，影响了对于性能退化趋势的精确跟踪.图6(b)对比了改进之前的SSE特征序列，该曲线随机波动性强，且并未体现出单调变化的主趋势.主要原因在于原有的符号化方式对于随机冲击过于“敏感”，使得性能退化的主要规律“湮没”在随机波动中.

图6 符号序列熵特征曲线对比Fig.6 Comparison of symbolic sequence entropy characteristic curves

采用模糊熵和样本熵(SE)算法对全寿命数据进行分析处理，参数如下：模糊熵相空间维数设置为4、相似容限度设置为r=0.5；样本熵相空间维数设置为4、相似容限度设置为0.5，常见的模糊熵和样本熵退化曲线对比如图7所示.由图7可知，两种基于熵的分析方法很难提取起升减速箱全寿命演化进程中的主趋势.主要原因在于全寿命数据中噪声和冲击成分较多，直接影响参数的取值.

图7 基于熵的退化曲线对比Fig.7 Comparison of degradation curves based on entropy

采用不同阈值因子时的ISSE演化曲线的对比分析如图8所示，其中：σ为标准差.由图8可知，4组曲线的整体趋势未变，但ISSE特征的值域以及阶段敏感性发生了变化.a取值越小，ISSE的值域越小，初期退化敏感性越高，后期退化曲线越平缓，敏感性越低；a取值越大，ISSE的值域越大，初期退化敏感性越低，后期退化趋势性明显，敏感性更强.主要原因在于阈值因子决定了符号化划分标准.当a值越小时，对弱冲击引起的模式变化越敏感，对强冲击的模式区分度越低.而减速箱性能退化的进程伴随着弱冲击成分越来越少，强冲击成分越来越多.因此，阈值因子a的取值决定了不同时期的性能退化敏感能力.为了兼顾性能退化整个过程的敏感性，本文选取阈值因子为G1标准偏差的2倍，即a=2σ.

图8 不同阈值因子的取值影响Fig.8 Influence of different threshold factors

3.3 O_ISSE在线特征提取

为了提高退化特征的稳定性，降低随机冲击对于特征准确性的影响，采用滑动窗口-Weibull拟合的方法提取尺度因子，以此作为起升减速箱的在线退化特征O_ISSE.设置滑动窗口宽度w=60，步长s=1.图9(a)为任意窗口Wq中的ISSE序列.采用Weibull分布验证序列的统计学规律，如图9(b)所示，其中：P为概率.数据统计概率呈近似直线型，符合Weibull分布.因此，采用Weibull分布挖掘其统计规律是有效的.

图9 滑动窗口Weibull分布拟合Fig.9 Weibull distribution fitting based on sliding window

对每组滑动窗口进行Weibull拟合，并提取尺度因子，得到的尺度参数γ演化曲线如图10所示.由图10可知，尺度参数能够准确地反映起升减速箱性能退化的趋势.与图6(a)中的ISSE曲线相比，尺度参数曲线更加平滑稳定，滤除了冲击成分的影响.因此，以尺度参数作为O_ISSE.

图10 在线退化特征提取结果Fig.10 Online degradation feature extraction results

图11(a)对比分析了窗口宽度参数w对在线退化特征提取结果的影响.由图11(a)可知，窗口宽度能够决定对于随机冲击成分的滤除能力.宽度越小，曲线的随机波动越明显，变化细节反映越充分；宽度越大，主趋势反映越明显.因此，可以根据实际需求设置恰当的滑动窗口宽度.从图11(b)可以看出，步长参数没有改变尺度参数的取值，步长越小，演化曲线的观测精度越高.因此，可以结合工业现场需求，选择合适的时间窗与步长大小.本文设置的滑动窗口参数为宽度w=60，步长s=1.

图11 参数影响对比分析Fig.11 Comparative analysis of parameter influence

3.4 退化状态评估

按照逻辑回归模型的建模步骤，首先选取健康和失效状态下的在线退化特征样本.本文选取前50组滑动窗的在线退化特征作为健康状态样本.考虑到退化特征S0的最大值为1，定义失效状态样本的退化特征为1，选取20组作为失效状态样本.定义健康状态H=0.95，失效状态H=0.05.采用70组训练样本进行逻辑回归模型训练.采用极大似然法计算得到模型参数：α=3.206 2，β=-6.139 0.将图10(a)中的在线退化特征序列输入至逻辑回归模型，得到未知样本的健康指数H值曲线如图12(a)所示.由图12(a)可以看出，起升减速箱的健康状态呈现整体下降的趋势，且呈现明显的阶段性.第430个滑动窗之前，健康指数基本上稳定在0.94附近，此时认为起升减速箱处于健康状态.之后，状态出现轻微的退化并存在一定的波动性，健康指数最低值约为0.78左右，此时认为起升减速箱处于轻微退化状态.约第940个滑动窗之后，设备出现明显的性能退化，健康指数下降到区间[0.2, 0.5]之间，并出现一定的波动性.此时认为起升减速箱处于严重退化状态.约第 2 000 个滑动窗之后，设备再次出现退化过程，健康指数最低值下降至0.12附近，并出现一定的波动，此时认为起升减速箱处于失效阶段.在约第 2 400 个滑动窗时，减速箱进行了检修，并更换了损坏的轴承.设备经过一定阶段的磨合之后，健康因子快速上升.达到运行初期的水平.图12(b)对比分析了以S0为退化特征时的H值曲线.由于S0特征曲线存在的波动性，使得健康指数曲线也存在较大的波动，很容易造成退化状态的误判.