缺失标记下基于类属属性的多标记特征选择

2021-11-05张志浩林耀进王晨曦

计算机应用 2021年10期

张志浩，林耀进*，卢舜，郭晨，王晨曦

（1.闽南师范大学计算机学院，福建漳州 363000；2.数据科学与智能应用福建省高校重点实验室（闽南师范大学），福建漳州 363000）

0 引言

多标记学习广泛应用于机器学习、数据挖掘和模式识别等应用领域［1-3］，多标记学习是指构建一个分类模型，将由特征向量描述的样本映射到多个类标记［4］。例如，在图像标注中，一幅图像可能同时具有“湖泊”“房屋”和“蓝天”等多个语义；在疾病诊断过程中，每个候诊病人可能同时具有心脏病、糖尿病和高血压等多种慢性疾病；在新闻网页分类中，一则体育报告同时含有多个相关主题，如：“篮球”“比赛”和“库里”。

同传统单标记学习一样，多标记数据的特征空间通常具有成千上万个特征［5-6］。例如，从图像中可以提取出数千个特征来表示其复杂的语义信息；然而，对于分类学习任务来说，许多特征是无关或者冗余的，并且这些无关或冗余特征往往给学习算法带来计算负担、性能不佳和过度拟合等问题。为处理该问题，相应的多标记特征选择算法被提出，用于降低多标记数据的高维性，以及提高分类算法的泛化性能。根据现有研究工作，可将多标记特征选择算法分成三大类：嵌入式、包装式和过滤式。嵌入式方法将特征选择过程嵌入到分类学习过程中，Zhang等［7］提出基于流形正则项约束的多标记特征选择算法；包装式方法需利用特定算法或模型评估特征子集，Gharroudi等［8］提出基于随机森林和标记依赖性的多标记特征选择算法；过滤式方法利用统计度量（如信息熵）评价特征，且该过程与分类器学习过程相互独立，Lin 等［9］提出通过最大化特征的依赖度并同时最小化特征间的冗余度来进行特征选择。

为提高多标记学习算法的性能，寻找每个标记对应的类属属性比利用所有属性进行分类更有效，即每个类标记往往与原始特征空间中一个特定的特征子集密切关联，该特征子集称为类属属性［10］。例如，在新闻分类中，“足球”“篮球”“奥运会”这类词（特征）能鉴别一则新闻是否是体育类新闻，而“股市”“货币”“证券”等词能鉴别一则新闻是财经类还是非财经类新闻。标记的类属属性是一组与该标记最相关、可辨别性最强的特征子集，可有效地挖掘类属属性与标记间的联系。因此，标记的类属属性能为多标记学习提供更加有价值的信息。

现有多标记特征选择方法一般假设训练样本的标记空间为完备的，并未考虑到标记缺失的情况，即训练样本的整个标记空间是提前给定的［7-9］。然而，在实际任务中获得完整的标记空间是非常困难的，原因在于为每个样本打上所有的类标记需要花费大量的人力物力；另外，类标记之间的歧义性容易导致漏标情况的出现。众所周知，标记空间的缺失会破坏原有的语义结构，使得标记的语义发生一定程度的变化，导致对挖掘标记之间的关系产生负面影响。为了解决缺失标记所带来的影响，根据多标记信息熵、线性回归和标记一致性等理论，许多缺失标记环境下的多标记特征选择算法被提出。例如，Wang 等［11］定义多标记信息熵和多标记互信息两个新概念，并运用特征交互进行特征选择；Zhu 等［12］运用鲁棒的线性回归模型选择最具区分性的特征，并且在特征选择的同时恢复缺失标记；Wu 等［13］用零元素为无符号标记定义缺失标记，利用标记一致性和标记平滑度假设重构不完整的标记矩阵。上述算法在处理缺失标记环境下的特征选择问题上具有一定成效，但未考虑每个类标记具有固有类属属性的情况，并且也未考虑如何利用标记固有类属属性恢复缺失标记。

根据以上分析可知，利用每个类标记的类属属性对提高缺失标记环境下多标记特征选择算法性能具有重要意义。基于类属属性固有性质，利用样本具有相同的特征值往往拥有一致标记的准则来最小化真实标记与预测标记间的差异，可实现缺失标记恢复。为此，本文提出一种缺失标记下基于类属属性的多标记特征选择（Multi-label Feature Selection based on Label-specific feature with Missing Labels，MFSLML）算法。该算法主要贡献如下：首先，通过稀疏学习方法为每个类标记选择类属属性；然后，在此基础上，利用线性回归模型构建标记与其类属属性的映射关系，用于恢复缺失的标记空间；最后，在7 组数据集上的实验结果表明，与现有特征选择算法相比，MFSLML性能更优。

1 所提模型

在多标记学习中，X=[x1，x2，…，xN]T代表样本的特征空间，其中xi∈Rd，d为特征维度，代表第i个样本共有d个特征；Y=[y1，y2，…，yN]T代表样本的标记空间，其中yi∈Rl，l为标记个数，所以N个样本可以表示为：S={(xi，yi)}。将标记值设置为yij=1、yij=0和yij=-1，yij表示矩阵Y中第i行第j列的元素，如果第i个样本具有第j个标记，则yij=1，反之，yij=-1，如果yij=0则无法明确第i个样本是否具有第j个标记，表示该标记缺失。

在本章中，提出一种缺失标记下基于类属属性的多标记特征选择算法，该算法主要有两个步骤：首先，考虑到每个类别标记具有固有类属属性，因此通过稀疏学习方法为每个类别标记选择固有类属属性；其次，为恢复缺失标记，根据所选类属属性，利用线性回归模型构建标记与其类属属性的映射关系用于恢复缺失标记。

1.1 类属属性学习

在实际多标记分类任务中，标记空间中每个类标记只与特征空间中一个特定的特征子集相关。于是，在特征选择过程中，可采用线性回归模型和平方损失函数学习一个特征权重的系数矩阵W。为保证选择的特征数量少且有代表性，在系数矩阵W上添加ℓ1范数正则项，则目标函数为：

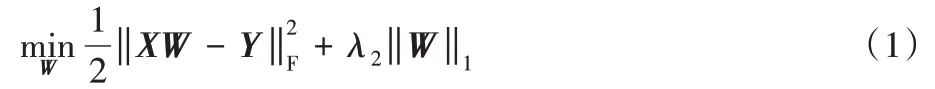
其中：X是样本的特征矩阵，Y是标记随机缺失的标记矩阵，W是学习得到的系数矩阵，λ2是参数。对于矩阵W，第i行表示为wi，第j列表示为wj，wij代表第i行第j列的元素值。wj中的非零元素决定了每个类标记的类属属性：若wij=0则表示第i个特征和第j个标记没有任何联系；若wij≠0，则表示第i个特征对于第j个标记具有鉴别能力。

1.2 缺失标记下基于类属属性的多标记特征选择

标记空间不完整会破坏原有语义结构，导致无法完整构建类属属性，使得样本特征信息难以准确刻画标记信息。针对缺失标记问题，采用恢复缺失标记的方法进行处理。首先，定义一个新矩阵Y*，在标记已知处，令在标记缺失处，设值为0。其次，在每一次迭代过程中，根据式（2）用学习得到的系数矩阵W以及特征矩阵X，更新Y*=XW中的缺失值，更新后的Y*将用于后续迭代过程。最后，利用式（3）将标记恢复成离散值，并令Y=Y*。

同时，为提高模型准确率，根据特征值相近的两个样本具有一致类别标记的准则，故目标函数可重写为：

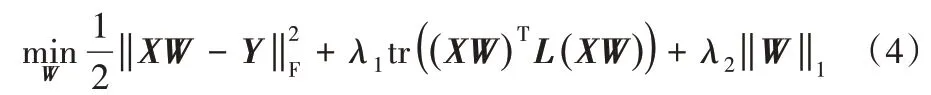
其中：tr((XW)TL(XW))代表一致性准则，L是Laplacian 矩阵，λ1和λ2是参数。参数λ1是控制模型中一致性准则的系数，而参数λ2控制每个类别标记固有类属属性的稀疏性。

为了清晰地阐述模型的计算过程，下文给出一个计算实例进行说明。

1.3 模型优化

由于式（4）中存在ℓ1范数正则项，且ℓ1范数是不光滑凸优化问题，因此，可利用加速近端梯度方法［14］进行求解，于是式（4）可变化为如下表达式：

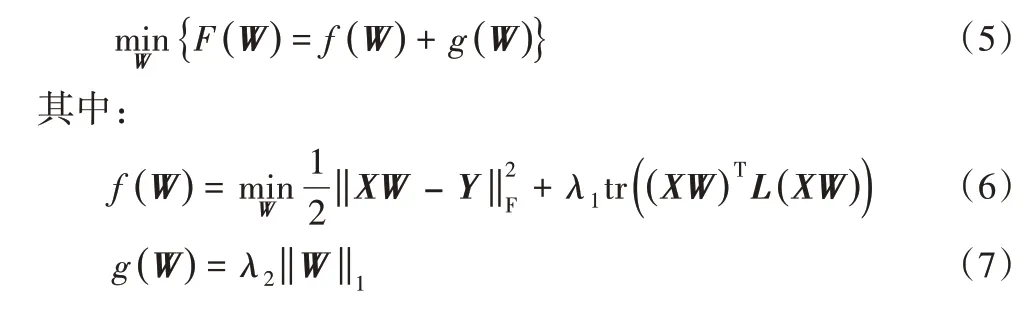
由于f(W)是一个凸优化问题，g(W)是一个不光滑凸优化问题，故上述优化问题可以转换成二次逼近序列优化问题进行求解：

1.3.1 更新W

在式（4）中优化目标只有一个未知变量W，故采用迭代优化方法进行求解。因式（5）中存在不光滑凸优化目标，则可定义以下优化目标求解W：

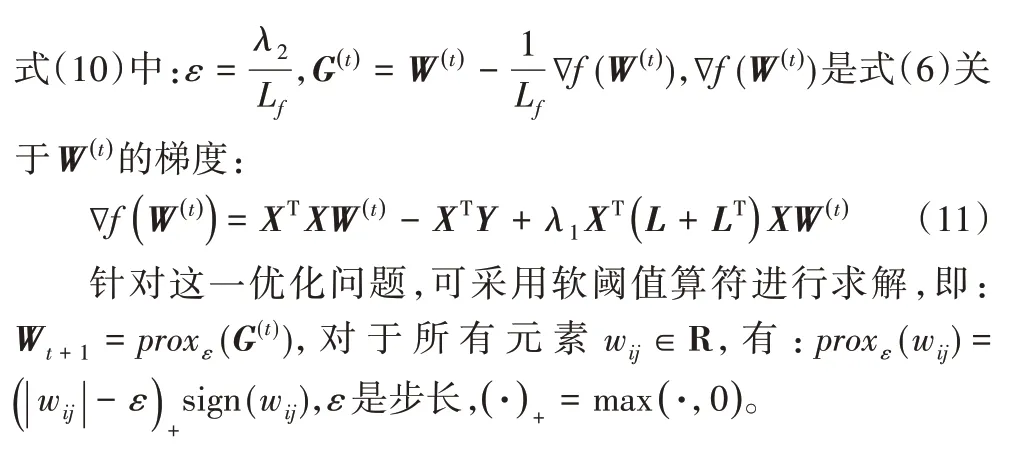
综上，可将W更新过程整理如下：

1.3.2 证明Lipschitz连续性

本节给出利普希兹连续性证明过程。假设存在参数W1和W2，将这两个参数分别代入式（11），可得：

其中Lf为Lipschitz常量。

根据式（4）所表示的优化目标，可提出缺失标记下基于类属属性的多标记特征选择算法，如算法1所示。

算法1 缺失标记下基于类属属性的多标记特征选择算法（Multi-label Feature Selection based on Label-specific feature with Missing Labels，MFSLML）。

输入训练样本矩阵X∈Rn×d，不完整训练样本标记矩阵Y∈Rn×l，参数λ1和λ2。

输出系数矩阵W*，恢复后的样本标记矩阵Y。

1.4 时间复杂度分析

在MFSLML 中，时间复杂度主要取决于步骤1、4和6。在步骤1 中，涉及到初始化，因此时间复杂度为O(d2n+d3+dnl+d2l)；在步骤4 中，计算Lipschitz 常量的时间复杂度为O(d3+l3)；在步骤6 中，需要计算f(W)的梯度，该步骤复杂度为O(d2l+dl2)，故t次迭代后总复杂度为O(t(d2l+dl2)) 。综上，算法时间复杂度为O(d2n+d3+dnl+d2l)+O(d3+l3)+O(t(d2l+dl2)) 。

2 实验设计与结果比较

2.1 实验数据

为了证明MFSLML 算法的有效性，从http：//mulan.sourceforge.net/datasets.html 选取7 组标准多标记数据集，其中，Arts、Computer、Entertainment、Recreation 和Reference 数据集被广泛用于文本分类任务中，Emotions 是音乐数据集，Scene 是场景图像数据集。表1 给出数据集的描述信息，训练样本和测试样本按照Mulan网站中的默认设置划分。

表1 多标记数据集例子Tab.1 Example of multi-label dataset

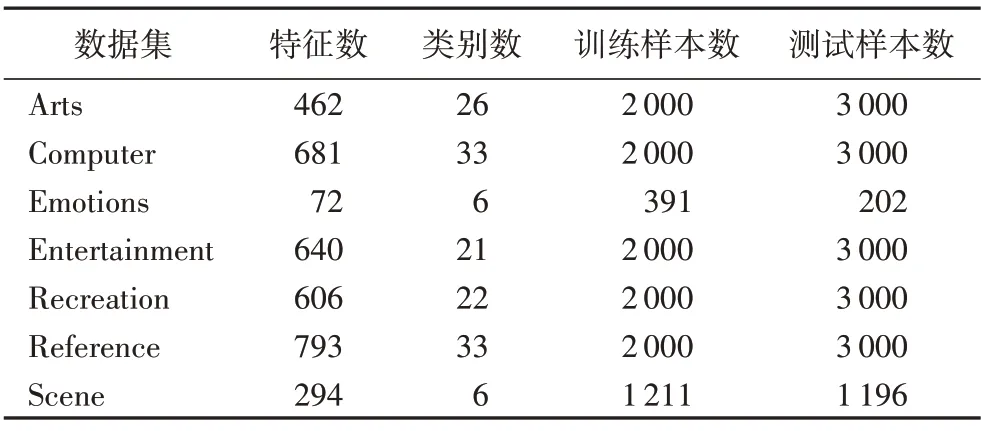
表2 本文所用的多标记数据集Tab.2 Multi-label datasets used in this paper

2.2 评价指标与对比算法

在本文实验中，采用平均查准率（Average Precision，AP）、覆盖范围（Coverage，CV）、海明损失（Hamming Loss，HL）和单错误（One Error，OE）四个评价指标，其中，AP指标取值越大越好，而CV、HL以及OE的取值则是越小越好。

给定一个测试集T={(xi，yi)|1 ≤i≤N}，假设yi⊆L为真实标记集合，⊆L为预测标记集合。4个评价指标具体计算公式如下：

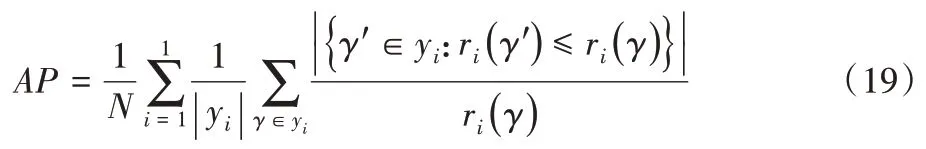
其中ri(γ)代表预测标记γ的排序。

其中rank(λ)代表预测标记λ可能排序位置。

其中：⊕代表异或运算，M代表集合中标记数目。

为了有效地验证MFSLML 算法性能，本文选择6 种流行的多标记特征选择算法进行比较：

MDDM（Multi-label Dimensionality reduction via Dependence Maximization）［15］该算法通过最大化特征和类标记之间的依赖关系，将原始特征空间投影到更低维的特征空间，其中包括MDDMspc和MDDMproj两种投影策略。

PMU（Pairwise Multi-label Utility）［16］该算法运用所选特征和标记集之间的互信息来处理特征选择问题。

MDMR（multi-label feature selection algorithm based Max-Dependency and Min-Redundancy）［9］该算法通过最大化特征的依赖度并同时最小化特征间的冗余度来进行特征选择。

MFML（Multi-label Feature selection with Missing Labels via considering feature interaction）［11］该算法定义多标记信息熵和多标记互信息两个新概念，并运用特征交互来进行特征选择，该算法能处理缺失标记环境下的特征选择问题。

MLMLFS（robust Multi-Label Feature Selection with Missing Labels）［12］该算法运用鲁棒的线性回归模型选择最具区分性的特征，该算法能处理缺失标记环境下的特征选择问题，并且在特征选择的同时恢复缺失标记。

2.3 参数设置

对于MFSLML 有两个参数，参照文献［17］将参数λ1和λ2设置在{10-6，10-5，…，103}范围内搜索最优值；对于MDDMspc和MDDMproj，根据文献［15］将参数μ设置为0.5；对于MDMR和PMU，采用等宽策略离散化连续型特征；对于MLMLFS，根据文献［12］将参数λ和α都设置为10-6。对于标记的缺失率，设置为0%，20%，40%。对于实验中用到的多标记分类器，与所有对比算法一样，采用经典的ML-KNN分类器［18］，其中参数Num和Smooth分别设置为10和1。

2.4 实验结果与分析

由于实验中算法最终都是得到特征排序，为了达到特征选择的目的，参照文献［9］，Arts、Computer 和Emotions 数据集取前15%个特征，剩下4 个数据集则取前20%个特征。表3～14 中运用“↑”符号来表示该评价指标的取值越大越好，运用“↓”符号来表示该评价指标的取值越小越好。此外，在每个表中，将最优的实验结果用黑粗体标出。

表3～5列出了7种特征选择算法在不同标记缺失率下，在评价指标Average Precision 上的实验结果；表6～8 列出了7 种特征选择算法在不同标记缺失率下，在评价指标Coverage 上的实验结果；表9～11 列出了7 种特征选择算法在不同标记缺失率下，在评价指标Hamming Loss 上的实验结果；表12～14列出了7 种特征选择算法在不同标记缺失率下，在评价指标One Error上的实验结果。

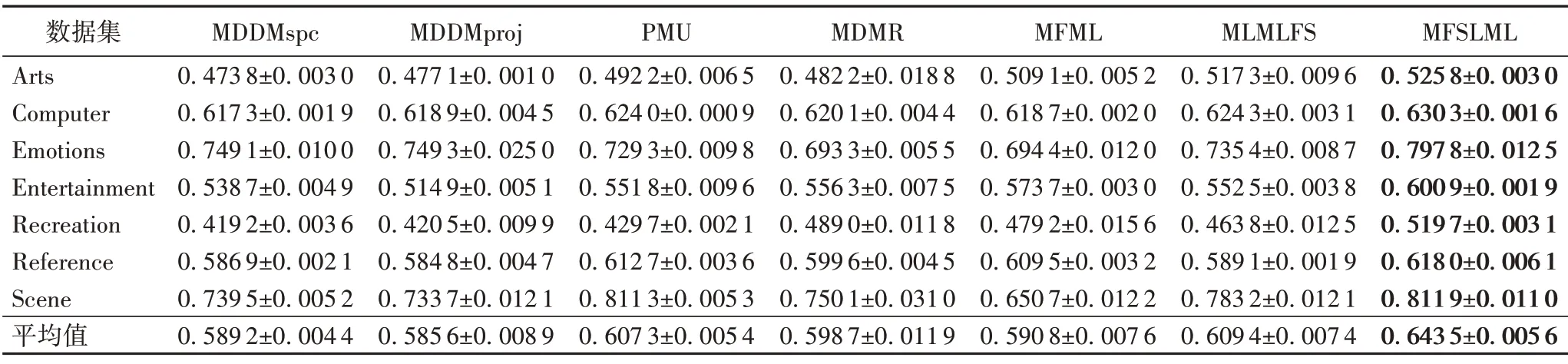
表3 0%标记缺失率下，7种特征选择算法的对比结果（Average Precision↑）Tab.3 Comparison results of 7 feature selection algorithms under 0%missing labels（Average Precision↑）

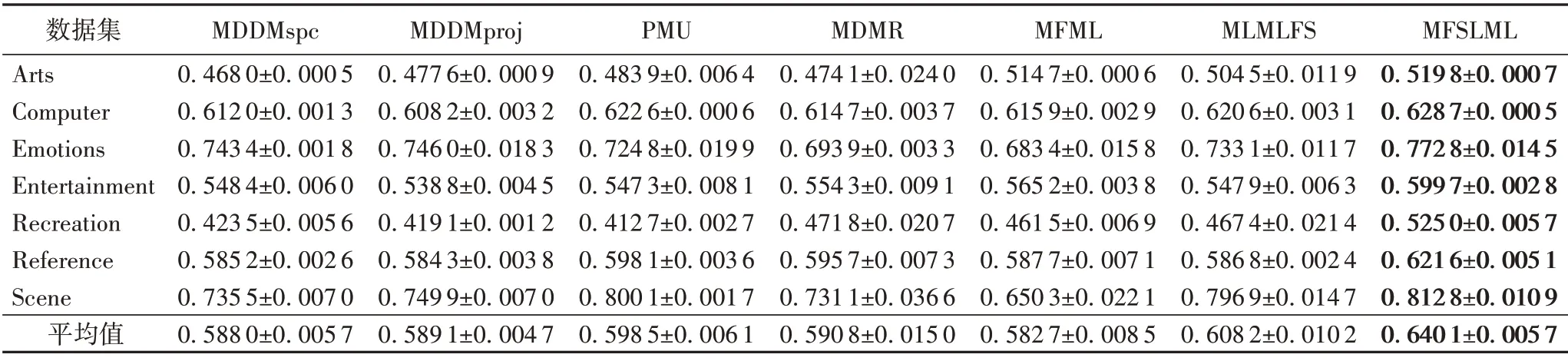
表4 20%标记缺失率下，7种特征选择算法的对比结果（Average Precision↑）Tab.4 Comparison results of 7 feature selection algorithms under 20%missing labels（Average Precision↑）

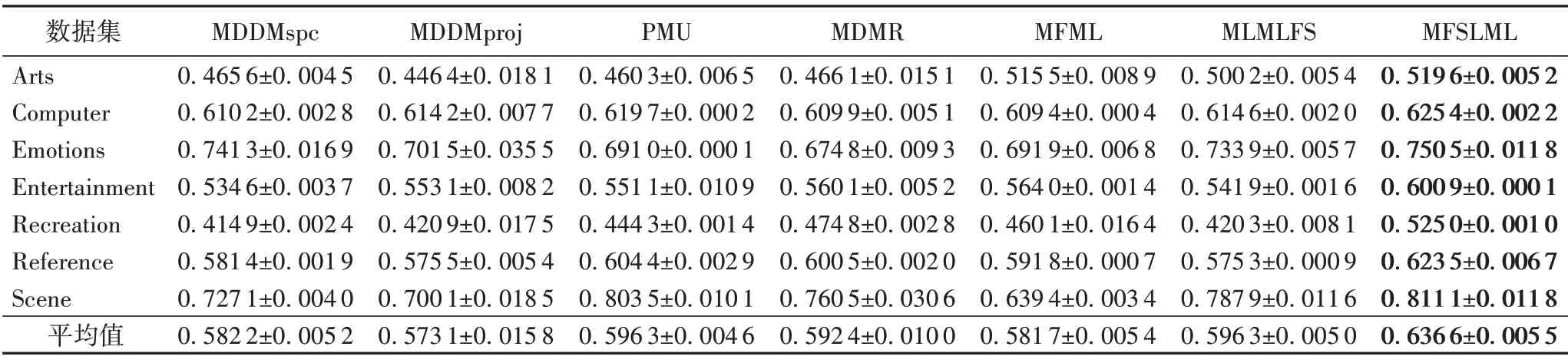
表5 40%标记缺失率下，7种特征选择算法的对比结果（Average Precision↑）Tab.5 Comparison results of 7 feature selection algorithms under 40%missing labels（Average Precision↑）

表6 0%标记缺失率下，7种特征选择算法的对比结果（Coverage↓）Tab.6 Comparison results of 7 feature selection algorithms under 0%missing labels（Coverage↓）

表7 20%标记缺失率下，7种特征选择算法的对比结果（Coverage↓）Tab.7 Comparison results of 7 feature selection algorithms under 20%missing labels（Coverage↓）

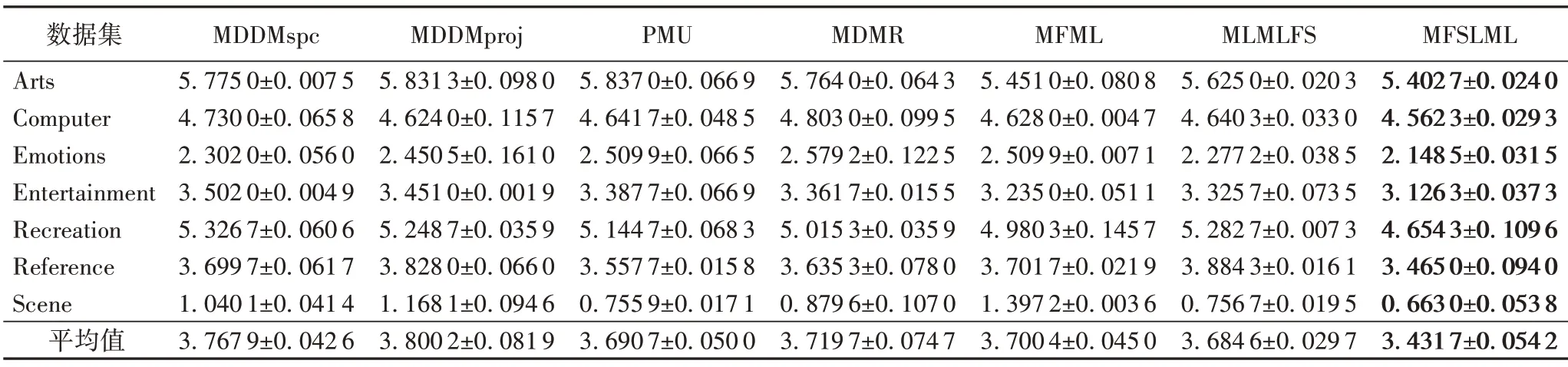
表8 40%标记缺失率下，7种特征选择算法的对比结果（Coverage↓）Tab.8 Comparison results of 7 feature selection algorithms under 40%missing labels（Coverage↓）

表9 0%标记缺失率下，7种特征选择算法的对比结果（Hamming Loss↓）Tab.9 Comparison results of 7 feature selection algorithms under 0%missing labels（Hamming Loss↓）

表10 20%标记缺失率下，7种特征选择算法的对比结果（Hamming Loss↓）Tab.10 Comparison results of 7 feature selection algorithms under 20%missing labels（Hamming Loss↓）

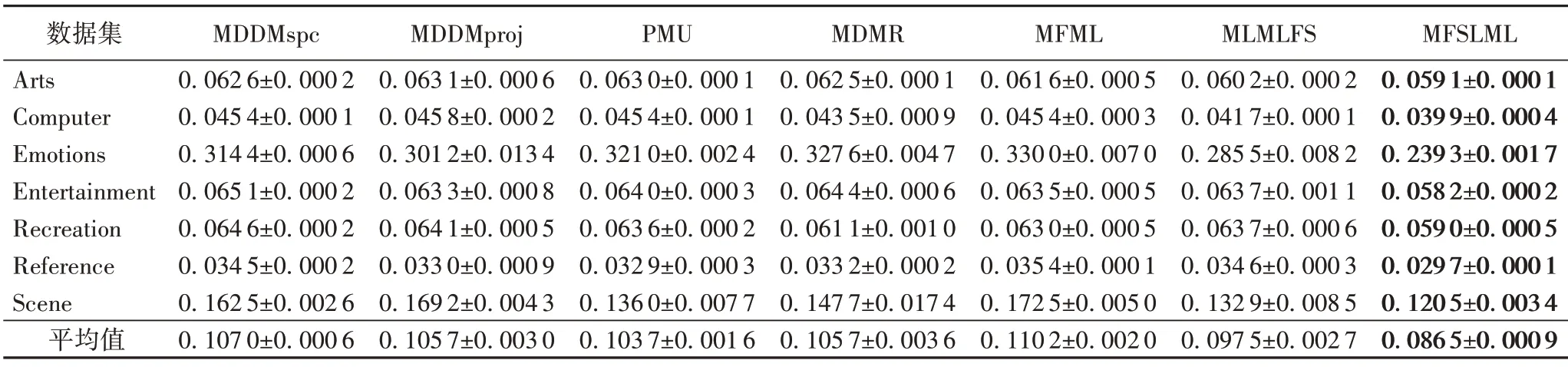
表11 40%标记缺失率下，7种特征选择算法的对比结果（Hamming Loss↓）Tab.11 Comparison results of 7 feature selection algorithms under 40%missing labels（Hamming Loss↓）

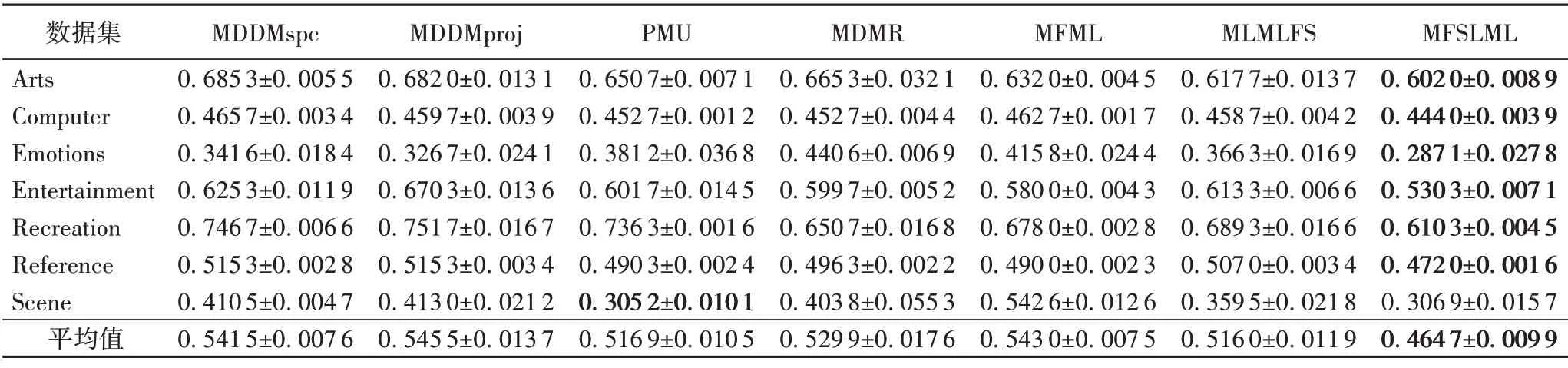
表12 0%标记缺失率下，7种特征选择算法的对比结果（One Error↓）Tab.12 Comparison results of 7 feature selection algorithms under 0%missing labels（One Error↓）

表13 20%标记缺失率下，7种特征选择算法的对比结果（One Error↓）Tab.13 Comparison results of 7 feature selection algorithms under 20%missing labels（One Error↓）

表14 40%标记缺失率下，7种特征选择算法的对比结果（One Error↓）Tab.14 Comparison results of 7 feature selection algorithms under 40%missing labels（One Error↓）

根据表3～14的实验结果可得出以下结论：

1）当缺失率为0%时，MFSLML 算法相当于完备的多标记特征选择算法。无论从4 个评价指标来看还是从平均性能来看，MFSLML 算法相比其他算法具有更优的分类性能，原因是在系数矩阵W上添加ℓ1范数正则项，能为每个类标记选择一组最有代表性的特征子集，即类属属性。

2）传统的多标记特征选择算法需要对特征空间和标记空间的关系进行建模，例如MDDM 算法考虑了特征和类标记之间的依赖关系，PMU 算法考虑了所选特征和类标记之间的互信息。但在缺失标记环境下，标记空间在一定程度上受到破坏，无法准确建模。对MFSLML算法而言，利用稀疏学习的方式学习每个标记的类属属性，然后通过线性回归模型恢复缺失标记，降低缺失标记带来的影响。故在五种缺失率的情况下，MFSLML 算法在7 组数据集上各个指标的平均分类性能都排第一。

3）随着缺失率增加，各方法的分类性能都出现不同程度的下降。与其他算法相比，MFSLML 算法的分类性能是缓慢下降的，原因在于该算法采用线性回归模型构建类属属性与标记的映射关系用于恢复缺失标记，因此MFSLML 算法在大多数情况下能取得最优结果。总体上看，MFSLML 算法的分类性能要优于其他算法，并且在缺失标记环境下进行特征选择时，恢复缺失标记非常重要。

由于所有对比算法均有采用Arts数据集展现所选特征数量对各算法分类性能的影响，为了公平比较，选取Arts数据集展示在3 种缺失率情况下不同算法在4 个评价指标上分类性能随着特征数目的变化趋势，具体做法如下：将各算法在Arts数据集下产生的特征排序中的特征依次放入MLKNN 分类器中训练，每放入一个特征记录一次结果。最终实验结果在图1～3中给出。

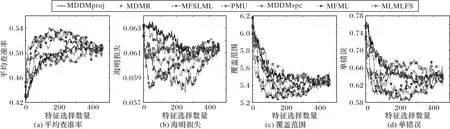
图1 0%标记缺失率下，在Arts数据集上的预测分类情况Fig.1 Predictive classification situation on Arts dataset under 0%missing labels

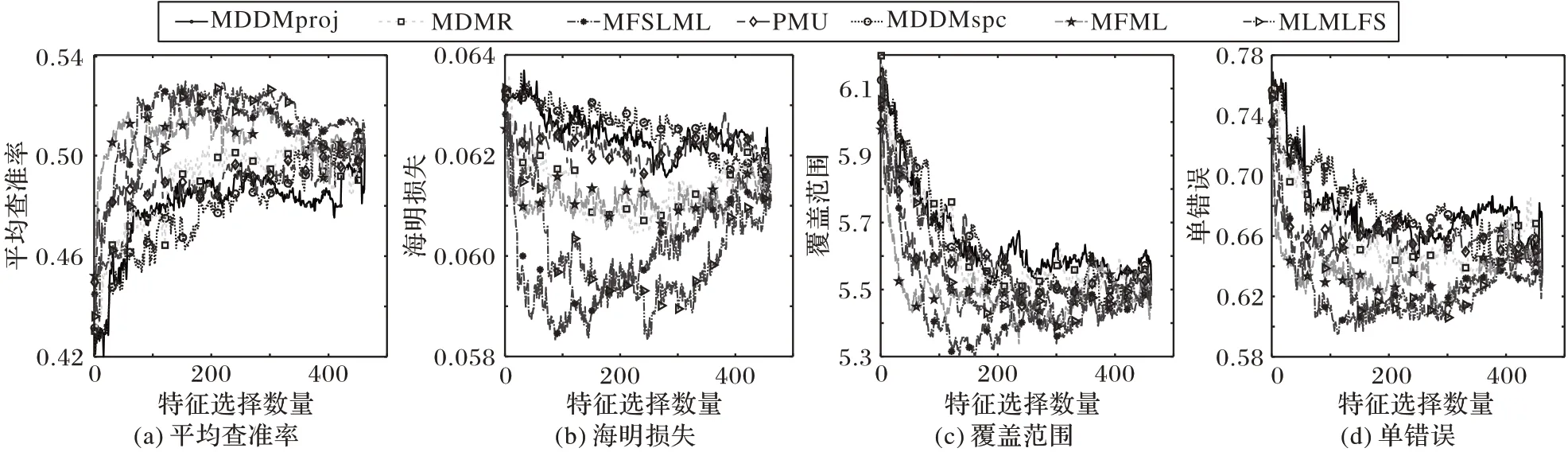
图2 20%标记缺失率下，在Arts数据集上的预测分类情况Fig.2 Predictive classification situation on Arts dataset under 20%missing labels

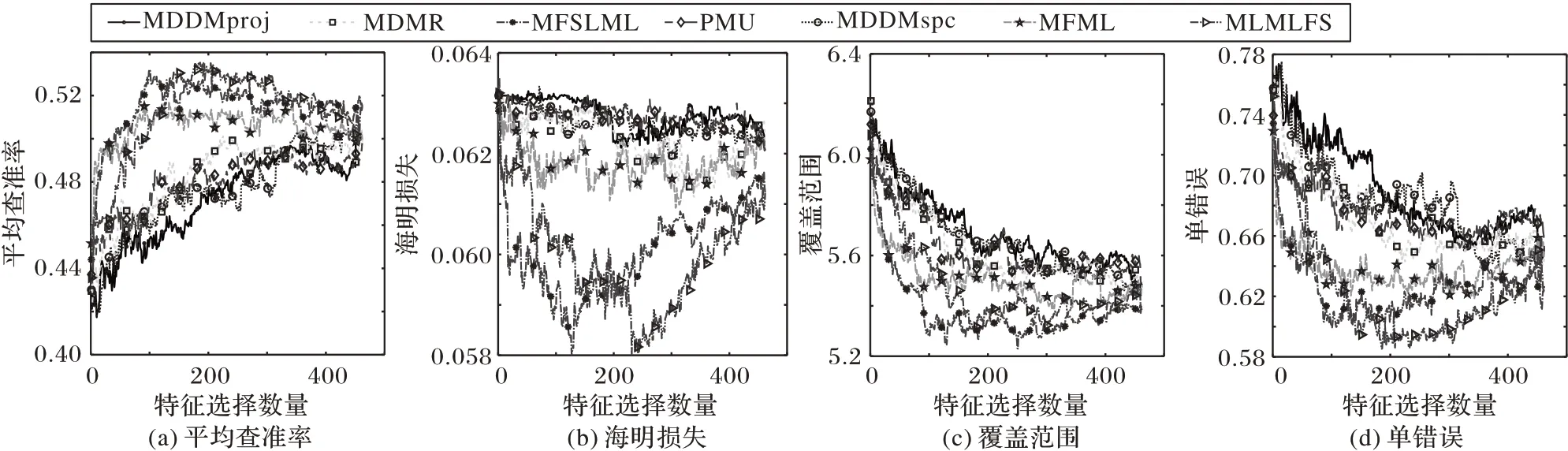
图3 40%标记缺失率下，在Arts数据集上的预测分类情况Fig.3 Predictive classification situation on Arts dataset under 40%missing labels

根据图1～3的实验结果可得出以下结论：

1）缺失率为0%时，MFSLML 算法在Hamming Loss 和Coverage 两个指标上优于其他算法，在其他两个指标上与其他算法无明显差距；缺失率为20% 时，MFSLML 算法在Hamming Loss 和Coverage 两个指标上表现优秀，在其他两个指标上只以微小优势胜出；缺失率为40%时，MFSLML算法在所有指标上均能得到更好的结果。

2）通过观察所有曲线，实验中每个评价指标都不是单调递增或者单调递减，表明并不是所有特征都有效，只有一个特征子集对分类性能影响最大。在大部分情况下，MFSLML 算法的最优预测分类性能都是在所选特征数量较少的情况下取得，说明MFSLML算法得到的特征排序更具代表性。

3）随着缺失率提升，所有算法的分类性能都呈下降趋势，但MFSLML 算法表现出更稳定的分类性能，从Coverage 这个评价指标可以看出，MFSLML 算法的效果要优于其他对比算法，特别是在缺失率较高时，这种优势更加明显，故相比其他算法MFSLML算法的预测分类性能具有更强的鲁棒性。