基于PCA和ARIMA的食品安全风险因素辨识及预测方法

沈霞芬，蔡强*，吴利芳，肖革新

1.浙江清华长三角研究院（嘉兴 314006）；2.国家食品安全风险评估中心（北京 100022）

食品安全是个综合概念，涉及卫生、质量、营养等多方面内容，以及种植、养殖、生产、包装、储存、运输、流通、消费等多个环节，单一的食品卫生、食品质量、食品营养等概念无法涵盖以上全部内容[1]。因此，关于食品安全，除了食品生产过程中所有指标需要满足特定的标准外，许多食品安全风险的存在和发展由食品供应链其他因素驱动，如空气、土壤、水等农业资源环境的影响，种养殖过程中化肥、农兽药等施用带来的影响，人体对食物的摄入量等[2]。这些因素与供应链之间的相互作用复杂，需要使用一种系统或整体的分析方法揭示其中的关系。目前，国内在食品安全风险领域的分析，主要以监管部门监督抽检和日常检查数据的风险分析为主，食品加工流通环节外其他因素的分析尚未形成深入挖掘。黄湘鹭等[3]对2016—2017年国家食品安全监督抽检的不合格项目进行归类分析，结果发现抽检合格率呈现稳中有升的趋势。李宗亮[4]以食品的污染物和营养物质为评价对象，以不合格率和不合格程度为评价指标构建食品风险系数评价体系，并结合BP神经网络模型，将食品风险系数应用于各类食品及抽检时待测参数的安全趋势预测预警等领域，为监管部门提供决策依据。相比之下，欧美发达国家的政府信息公开工作具有起步早、数据多、深度开放等特点，在食品安全分析方面也有着更进一步的研究[5]。Yamine等[6]使用贝叶斯网络模型来识别和量化RASFF中关于源自印度、土耳其和荷兰的水果和蔬菜的所有食品安全通告数据与产品原产国气候因素、农业因素和经济因素之间的关系，研究结果表明不能确定气候因素对蔬果化学食品安全危害产生影响。Alberto等[7]根据联合国粮食及农业组织提供的关于进出口和生产的公开数据，构建数学模型模拟粮食产品的分配情况，首次从食品安全风险的角度论证网格结构对食品分布影响。

从食品安全多个影响因素的综合分析与关键风险因子确定，以及单一指标数据的预测2个角度探讨食品安全风险分析的数据模型，并给出相应的应用实例。

1 材料与方法

1.1 材料

1.1.1 数据来源

食品安全涉及从农田到餐桌的整个过程，理论上需要收集覆盖食品供应链上的所有数据，同时融合时空、地理、环境、气象及医疗健康等信息。但国内目前尚未建立统一的数据标准，也尚未解决跨层级、跨部门、跨业务、全链条多源异构数据的融合，所以数据收集十分困难。为既兼顾各指标的合理性、时间上的统一又不失数据的准确性，从国家统计局官网上收集1999—2018年关于中国环境、农业因素及消费量的6个食品安全评价指标数据，数据维度为6×20。同时，以“食物中毒事件”为关键词，通过国家卫生健康委员会官网（http：//www.nhc.gov.cn）检索的“卫生部办公厅关于XXXX年全国食物中毒事件情况的通报”文件中，收集2008—2015年公开发布的中国食物中毒事件起数的月度数据，数据长度为96条。

1.1.2 分析软件

采用R对食品安全6个影响因素进行主成分分析，并对食物中毒事件起数季度数据进行时间序列分析。以α=0.05为检验水准，p＜0.05说明具有显著性差异。

1.2 方法

1.2.1 多影响因素的综合分析

采用主成分分析法从多个影响因素入手，提取主要成分，并基于成分的方差贡献率计算综合评分，以此作为各影响因素对年度食品安全的影响程度。采用灰色关联度分析，计算食品安全影响因素与综合评分之间的关联度，确定最为关键的要素。

1) 构建一个m×n的矩阵X，行表示年份，列表示食品安全的影响因素。

2) 采用Z-score对以上n个指标进行标准化使其量纲统一，得到1组新变量（z1,z2,…,zn）[8]，并计算这组新变量的相关系数矩阵R。

3) 由相关系数矩阵R计算得到其特征值λ，并从大到小排序，λ1≥λ2≥…≥λn≥0，且计算各特征值对应的特征向量εi=（εi1,εi2,…,εin），i=1,2,…,n，确定X的第i个主成分。

4) 采用灰色关联度计算各评价指标Xi与综合评分Y之间关联度[9]，关联系数定义为：

式中：i为第i个评价指标；k为各指标的第k个数值，故Y(k)为综合评分Y的第k个数值，Xi(k)为第i个评价指标的第k个数值；ρ为分辨系数，取值为（0,1），ρ越小，区分度越低，一般取值为0.5。

由于关联系数是比较数列与参考数列在各个时刻的关联程度值，所以它是一个序列，信息过于分散不便于进行整体比较。因此需要将各时刻的关联系数求其平均值，作为比较数列xi与参考数列Y之间关联度的数量表示，关联度ri定义为：

ri越大，表明指标i对综合评分的影响越大。

1.2.2 单一指标数据的预测分析

对单位时间内某个指标数据进行统计，如在农业生产中，农兽药和化肥的使用量可按季度、按月记录；加工运输环节中，食品生产件数、检验检测信息等可按周、按天记录，这些数据便为时间序列。对于数据都为正值的时间序列，可通过5个步骤完成模型构建及分析。

1) 对于非线性的变量进行对数变换，消除数据的非线性，且不改变数据之间的统计性质。

2) 对于非平稳的变量进行差分变换，弱化随机性使其平稳化。利用ADF单位根检验，检验变换后的序列是否平稳。具体方法：原假设H0，序列非平稳；备择假设H1，序列平稳。检验统计量小于5%临界值时拒绝原假设，即认为该序列平稳。

3) 对d阶差分后的平稳时间序列构建ARIMA模型，若模型残差的Ljung-Box统计量的p值大于0.05，则模型通过检验[10]，再利用所构建的模型进行预测。

2 结果与分析

2.1 食品安全综合评价及关键影响因素确定

2.1.1 食品安全风险的影响因素

选取的食品安全风险指标包含1999—2018年环境、农业因素和消费量等数据。食品安全风险与各影响因素值的大小呈正比。

2.1.2 食品安全风险的综合评分

从标准化后各影响因素的散点图矩阵来看，除了废气排放量与其他几个指标的相关性较弱之外（各点越接近矩形的对角线表明相关性越强），其余指标之间都具有一定的相关性，存在一定的信息重叠（图1）。主成分分析选取的前2个主成分的特征值分别为3.34和2.27，前2个主成分的累计贡献率达93%，基本包括原来那些变量所包含信息。

图1 食品安全影响因素的散点图矩阵

由2个主成分加权所得的综合得分，代表着环境、农业和消费因素对食品安全的影响程度（表2）。

表2 1999—2018年食品安全影响因素的综合评分

结果表明，环境、农业及消费量对中国食品安全风险的影响具有阶段性：1999—2002年中国食品安全风险逐年降低；2002—2012年食品安全风险基本上呈现逐年升高趋势；直到2012年之后又基本上恢复到逐年降低趋势。产生该结果的主要原因在于工业与经济的发展加速了环境污染及农业生产过程中农兽药与化肥的使用量，导致2002—2012年食品安全的风险逐渐增高，但以牺牲环境与国民健康的工业和经济发展打破中国可持续发展的基本理念。“十八大”之后政府开始出台各种环保与民生健康的政策[11-12]，使得工业废弃物及农业生产过程中化学品的投入量有所控制，因此食品安全风险在2012年后呈现明显降低趋势。

表1 食品安全风险因素

2.1.3 食品安全关键影响要素确定

灰色关联度分析得到各影响因素与食品安全风险综合评分之间的关联度分别为0.637，0.663，0.682，0.741，0.714和0.598。因此1999—2018年影响中国食品安全的因素排名依次为单位面积农兽药使用量、单位面积农用化肥施用折纯量、废气（二氧化硫+烟粉尘）排放量、废水排放量、工业固体废物倾倒丢弃量、居民主要食品人均消费量。该结果表明，单从环境、农业和消费层面来看，农业生产过程中投入的化学品量对于中国食品安全来说是最为显著的影响因素，其次为环境因素。为减轻病虫草害对产量的威胁并获得高产，农民对于农兽药和化肥不合理使用的行为比较普遍。陈晓明等[13]表明1991—2013年中国农药使用量增长135.5%，不合理的使用行为导致其残留物在食物链中不断传递和迁移[13]。史常亮等[14]指出中国每公顷耕地化肥施用量由1980年的127.8 kg增加到2013年的437.4 kg，是国际公认化肥施用安全上限225 kg/hm2的1.94倍。过度使用化肥产生的污染土壤的重金属和放射性物质，通过食物链不断在植物和生物体内富集，最终在人体内积累危害人体健康。

2.2 时间序列分析预测食品安全风险

2.2.1 季节性分布结果

2008—2015年全国食物中毒事件起数总体上呈现先降低后增高趋势（图2），并且存在明显季度模式。第3季度的食物中毒事件呈现年度最高，第2季度次之，第1季度最低。因此，以季度作为时间单位，对食物中毒事件做时间序列预测将更具准确性。

图2 2008—2015年全国食物中毒事件起数的月度数据时序图

2.2.2 平稳性检验结果

消除非线性后的季度食物中毒事件序列，经过1阶差分后还是存在季节与非季节相关性（图3a2）；经过1阶季节差分后的序列消除相关性（图3a3）；经过1阶差分及1阶季节差分后的序列在滞后1阶和5阶上还是存在一定程度相关性（图3a4）。

图3 食物中毒事件对数序列及其差分后序列的自相关（ACF，a）和偏自相关（PACF，b）函数图

平稳性检验结果表明，除了食物中毒事件起数的对数序列外，其他经过差分处理后序列都平稳（p＜0.05），符合ARIMA模型建立的条件（表3）。

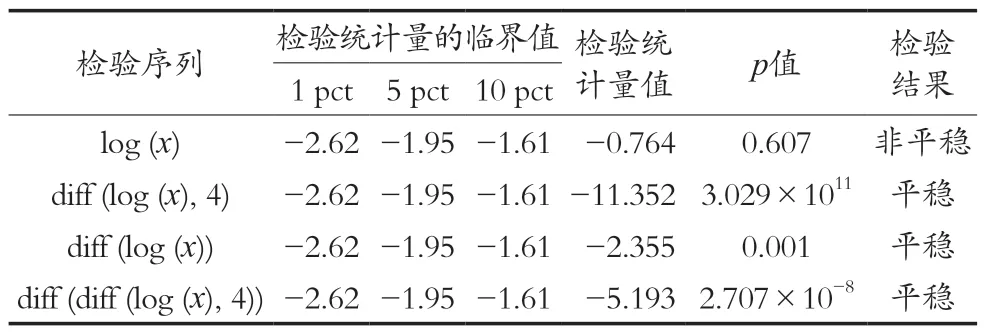
表3 所有序列的平稳性检验结果

2.2.3 ARIMA模型及预测结果

根据差分后序列的自相关（ACF）和偏自相关（PACF）函数图（图3）建立3个ARIMA模型（表4），模型残差的Ljung-Box统计量的p值及残差检验图均表明3个模型通过检验。

表4 根据自相关（ACF）和偏自相关（PACF）图确定ARIMA模型的拟合优度指标

表5为由R自动选取的ARIMA模型。其中，ARIMA (3,1,0)等同于表4中第一个模型，但由于调用的是R中的不同函数，所以在结果上略显差异；考虑季节性的模型，R自动选择的是ARIMA(0,1,1)×(0,1,0)4，虽然模型残差的Ljung-Box统计量的p值大于0.05，但相比于其他几个模型的p值小很多，且残差检验图显示，残差在滞后5阶及其后面的阶数上存在较小相关性。

表5 R自动选择ARIMA模型的拟合优度指标

以AIC最小原则，选择最好解释数据但含最少自由参数的模型ARIMA(5,0,0)×(0,1,0)4，即：

作为全国食物中毒事件起数的时间序列模型。模型的拟合值与真实值的变动具有较高的一致性（图4a）。该模型对2015年度中毒事件起数的预测显示出较强的季节性，预测2015年第3季度的中毒事件数仍然是全年最高，达到66件；第1季度和第4季度的中毒事件起数相对较低，分别为16和27件；第2季度的中毒事件起数全年第二，为35件。产生该结果的主要原因是春夏秋季节天气温热、气候湿润，适宜细菌和有毒植物的生长繁殖，成为食物中毒事件的高发期。从预测效果上来看，该模型对2015年第2季度的预测完全吻合，除了第1季度稍有偏差外，其余3个季度预测效果较好，真实值都位于95%的预测区间内[7]（图4b）。

图4 模型ARIMA(5,0,0)×(0,1,0)4的拟合结果（a）与预测结果（b）

3 结论

食品安全风险分析是一个针对复杂系统的综合性评价问题。主成分分析与灰色关联度结合能够客观、全面地反映各项影响因素的信息，同时通过估计综合评分与各影响因素之间的一致性程度判断出最为关键的影响因素。在食品领域，由于气候变化、饮食习惯等因素的影响，很多食品安全相关的数据具有周期性。时间序列ARIMA模型能够根据某个指标的历史数据，通过计量的手段反映时序中动态依存关系，不仅从数量上揭示该指标的发展变化规律，而且能够准确预测未来走势。

然而，在食品领域，食品安全的影响因素不仅是环境、农业和消费因素，还关系到食品生产和流通过程中食品质量等问题，理论上需要实现对食品从农田到餐桌的全面评价。但由于目前国内食品链上各环节信息化水平不一，一些环节数据采集缺失，数据存储没有统一的标准，使得食品安全的综合评价缺乏全面性。但从分析方法上来说，主成分分析与时间序列分析对于食品安全领域多因素的综合评价和单一指标的预测分析都具有较好的指示作用。