尊重规律 回归本真——从变压器中一个被普遍误认为“正确”的结论说起

夏季云

（南京市第一中学，江苏 南京 210001）

很多高中物理教辅材料中都能看到下面的一道题，该题认为是一道经典题目，本文对该题及其引发的悖论进行分析.

1 悖论引发质疑

原题.想一想：如图1所示理想变压器的原、副线圈匝数之比为4∶1，平行金属导轨与原线圈相连.

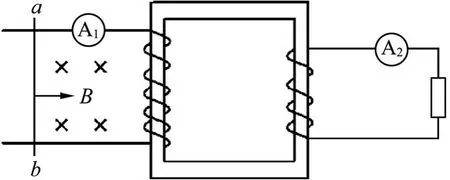
图1

（1）当导体棒ab在匀强磁场中匀速运动时电流表A1的示数为12mA，则电流表A2的示数为________mA.

（2）当导体棒ab做匀加速运动时，A2的示数会怎样变化？

（3）若导体棒ab做变加速运动，则A2的示数又会怎样呢？

参考解析：（1）原线圈中有恒定的电流I1，线圈中产生磁通量恒定，即，所以副线圈中

（2）当导体棒做匀加速运动时，E1、I1都发生变化，但是磁通变化率是恒定的，在副线圈中有恒定的E2、I2.

（3）若导体棒做变加速运动，则E1、I1相应的非均匀变化，副线圈中将会产生随时间变化的电流.

悖论引发质疑：对（2）的结论再作推理，对原线圈有U1=E1，E1在均匀增加；对副线圈有U2=E2，E2保持不变.由此得到原、副线圈电压关系不遵循变压器的电压比规律.悖论由此形成，问题在哪里？

2 高中教学中关于电磁感应的几个问题是造成错误认知形成的根源

问题1.导体棒与定值电阻构成回路，导体棒切割磁感线运动.

例1.如图2所示，左端接有阻值为R的定值电阻且足够长的平行光滑导轨CE、DF的间距为L，导轨固定在水平面上，且处在磁感应强度为B、竖直向下的匀强磁场中，一质量为m、电阻为r的导体棒ab垂直导轨放置在导轨上静止，导轨的电阻不计.某时刻给导体棒ab一个水平向右的瞬时冲量I，导体棒将向右运动，最后停下来，则此过程中导体棒的运动有什么规律？

参考解析：导体棒获得向右的瞬时初速度后切割磁感线，回路中出现感应电流，导体棒ab受到向左的安培力，向右减速运动，设运动过程中某时刻的速度为v，加速度为a，则有v反向，导体棒做减速运动，v减小时，a减小，当a=0时，v=0，所以导体棒做的是加速度越来越小的减速运动，最终静止.

反思：从提供的解析发现，导体棒产生的电动势是电路中的唯一电源.事实上一根导体棒运动时产生的感应电动势非常小，教学中为了研究问题的方便和让学生更简单地理解，把小量当成了大量来处理，忽略了它的客观真实性.

问题2.导体棒与定值电阻、电源构成回路，导体棒在安培力作用下运动.

例2.如图3所示，水平放置的光滑平行金属导轨，左端通过开关S与内阻不计、电动势为E的电源相连，右端与半径为L=20 cm的光滑圆弧导轨相接.导轨宽度为20 cm，电阻不计.导轨所在空间有竖直方向的匀强磁场，磁感应强度B=0.5 T.一根导体棒ab垂直导轨放置，质量m=60 g，电阻R=1Ω，用两根长也为20 cm的绝缘细线悬挂，导体棒恰好与导轨接触.当闭合开关S后，导体棒沿圆弧摆动，摆动过程中导体棒始终与导轨接触良好且细线处于张紧状态.导体棒ab速度最大时，细线与竖直方向的夹角θ=53°（已知sin53°=0.8，cos53°=0.6，g=10 m／s2），则

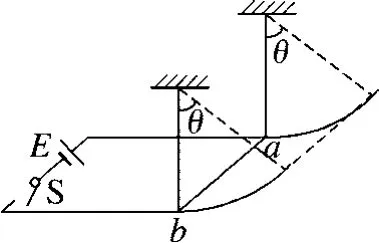
图3

（A）磁场方向一定竖直向上.

（B）电源的电动势E=8 V.

（C）导体棒在摆动过程中所受安培力F=8 N.

（D）导体棒摆动过程中的最大动能为0.08 J.

参考解析：由题意知，当开关S闭合时，导体棒向右摆动，说明其所受安培力水平向右，由左手定则可知，磁场方向竖直向下，故选项（A）错误；设电路中电流为I，电源的电动势为E，导体棒ab所受安培力为F，导体棒ab速度最大时，细线与竖直方向的夹角θ=53°，则，得F=0.8 N，E=8 V，故选项（B）正确，选项（C）错误；导体棒ab速度最大时，动能最大为Ekm，根据动能定理得FLsin53°-mgL（1-cos53°）=Ekm-0，解得Ekm=0.08 J，故选项（D）正确.

反思：从提供的解析发现，计算回路电流时没有考虑导体棒产生的反电动势.例1与例2对导体棒电动势两种不一样的处理让好的学生产生了困惑.事实上例2中导体棒运动时一定产生了感应电动势，只不过该电动势远小于电源的电动势，在计算回路电流时忽略了.

问题3.导体棒与导体环构成回路，导体棒做切割磁感线的运动.

例3.如图4所示，在一有界匀强磁场中放一电阻不计的平行金属导轨，虚线为有界磁场的左边界，导轨跟圆形导体环M相接，图中导体环N与导体环M共面、彼此绝缘，且两线圈的圆心重合，半径RM＜RN.在磁场中垂直于导轨放置一根导体棒ab，已知磁场垂直于导轨所在平面向外.欲使导体环N有收缩的趋势，下列说法正确的是

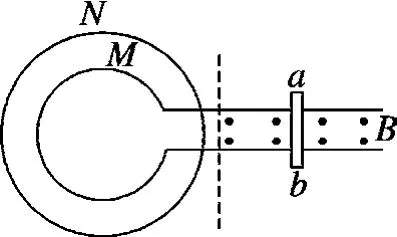
图4

（A）导体棒可能沿导轨向左做加速运动.

（B）导体棒可能沿导轨向右做加速运动.

（C）导体棒可能沿导轨向左做减速运动.

（D）导体棒可能沿导轨向左做匀速运动.

参考解析：导体棒ab加速向左运动时，导体棒ab中产生的感应电流增大，由右手定则判断知ab中电流方向由b→a，根据安培定则可知M产生的磁场方向垂直纸面向外，穿过N的磁通量均匀增大，线圈面积越大抵消的磁感线越多，所以线圈N要通过增大面积以阻碍磁通量的增大，故选项（A）错误；导体棒ab加速向右运动时，导体棒ab中产生的感应电流增大，由右手定则判断知ab中电流方向由a→b，根据安培定则判断可知M产生的磁场方向垂直纸面向里，穿过N的磁通量均匀增大，同理可知选项（B）错误；导体棒ab减速向左运动时，导体棒ab中产生的感应电流减小，由右手定则判断知ab中电流方向由b→a，根据安培定则判断可知M产生的磁场方向垂直纸面向外，穿过N的磁通量均匀减小，线圈面积越大抵消的磁感线越多，所以线圈N要通过减小面积以阻碍磁通量的减小，故选项（C）正确；导体棒ab匀速向左运动时，导体棒ab产生的感应电流恒定不变，线圈M产生的磁场恒定不变，穿过线圈N中的磁通量不变，没有感应电流产生，则线圈N不受磁场力，没有收缩的趋势，故选项（D）错误.

反思：从提供的解析发现，计算回路电流时没有考虑导体环M产生的自感电动势.事实上导体棒切割磁感线产生电动势对回路供电时，导体环中一定产生了自感电动势，只不过由于导体环自感系数较小，该自感电动势很小，实际上导体棒的电动势也不大，在计算回路电流时忽略自感电动势，但为什么忽略往往并没有说明.（A）、（B）、（C）选项解释时均提到“均匀”变化.

问题4.自感现象的通电自感实验中，电路稳定后线圈中没有自感电动势.

例4.如图5所示的电路中，A1和A2是完全相同的灯泡，线圈L的电阻可以忽略，下列说法中正确的是

图5

（A）闭合开关S接通电路时，A2始终比A1亮.

（B）闭合开关S接通电路时，A2先亮，A1后亮，最后一样亮.

（C）断开开关S切断电路时，A2先熄灭，A1过一会儿才熄灭.

（D）断开开关S切断电路时，A1和A2都要过一会儿才熄灭.

参考解析：闭合开关S接通电路，A2立即亮，线圈对电流的增大有阻碍作用，所以通过A1的电流慢慢变大，最后两灯泡的电压一样大，所以一样亮，故选项（A）错误，选项（B）正确；断开开关S切断电路时，线圈对电流的减小有阻碍作用，相当于电源，与A1和A2串联，所以两灯泡都要过一会儿熄灭，故选项（C）错误，选项（D）正确.

反思：从提供的解析发现，基于实验现象发现的规律，认为线圈对电流的增大有阻碍作用，所以通过A1的电流慢慢变大，但A1的电流是由什么因素决定并没有做分析和推理.事实上，自感的作用是阻碍变化，但电流还是要发生变化，变化过程中的电流是由外加电源和自感电动势共同决定，回路电流会变化到一定值，稳定时表示磁通量不变化，也就不会产生自感电动势，此时电流是由外加电源决定.因此计算回路稳态电流时，由于线圈不产生自感电动势，两灯亮度一致.

通过以上4个阶段的累积给学生造成以下事实性结论：一根棒主动切割产生的电动势是要考虑；一根棒切割产生的反电动势是不要考虑；导体环产生的自感电动势不要考虑；线圈产生的自感电动势要考虑，且自感电动势是由外加电源形成的电流产生的磁通量产生；与线圈相连的电源电动势均匀增加时，回路电流均匀增加，线圈通过的磁通量也均匀增加.

教师认为高中电磁感应中从棒到线圈的电动势教学结构已经完成，学生也已经形成了一个相对固化的认知，对解决一般问题学生也能得心应手，教学也算完备了.但是，前面的教学显然背离了教育本真，对理想化处理解释不到位，对周期性变化和趋稳态变化的区别分析不到位，对自感的变化过程没有进行分析推理，这也为变化过程与变化稳态的混淆埋下了祸根，让学生误以为带有线圈的回路电流仅是由外加电源决定.由以上分析不难发现，由于变压器原线圈加的是周期性变化的电流，回路中电流一直在变化，但学生的认知规律还是稳定态思维解决问题占了主导，那么对变压器相关问题产生的错误认知也不奇怪了.

3 回归学生本真，基于高中学生认知规律，帮助学生养成科学推理习惯

3.1 理想化处理是有前提的

（1）前述例1这样做的目的为了减小学习的难度，这里理想化处理不影响问题讨论的本质；例2，例3中反电动势相对外加电源是个次要因素，因而可以被忽略；例4中变化过程与稳定状态是不一样的，外加电压恒定是变化中的一种特殊情况，它的规律不能代表变化电压的特点，这一点不弄清楚也为本文所说的错误“奠定了基础”.

（2）理想变压器模型应忽略的次要因素.

① 不计漏磁，即通过原副线圈每匝线圈的磁通量都相等，因而不计磁场能损失；

② 不计原副线圈的电阻，因而不计线圈的热能损失；

③ 不计铁芯中产生的涡流，因而不计铁芯的热能损失.

综上，理想变压器在传输能量时没有能量损失.

根据法拉第电磁感应定律，原、副线圈产生的感应电动势分别为

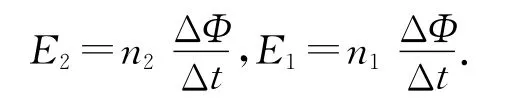
因理想变压器不计原、副线圈的电阻，则线圈两端的电压等于它产生的感应电动势，即U1=E1，U2=E2，联立以上各式可得

3.2 区分好状态与过程，培养科学推理习惯

教材中在讨论自感现象时，外加电压是恒定的，回路电压很快会达到稳定，自感电动势消失，回路电流是由外加电动势决定，这是状态分析的思维方式.在LC振荡电路中如果是电容器放电过程，根据电场能与磁场能总量一定，电容器极板间电压越小，回路电流反而越大，回路中电流是由电容器极板间电压和线圈自感电动势共同决定，尽管电容器极板间电压减小，但线圈自感电动势减小得更多，结果回路电流还是呈增加，这是过程思维的方式.

科学推理是指依据物理概念、规律、方法、证据、逻辑进行严密论证，从而发现结论的过程.推理流程图如图6.

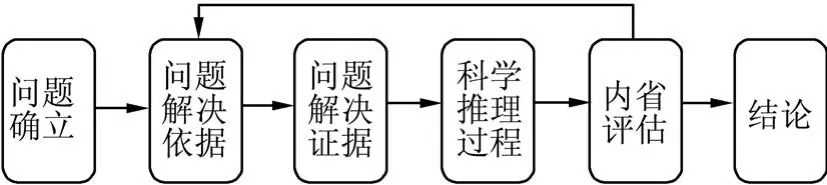
图6 推理流程图

4 回归物理学科的本真，基于高中学习要求，帮助学生建立科学认知

4.1 高中物理教材关于变压器的原理[1]

原线圈和副线圈中的电流共同产生的磁通量，绝大部分通过铁芯，只有一小部分落到铁芯之外，在粗略的计算中可以略去漏掉的磁通量，认为穿出这两个线圈的交变磁通量相同，因而这两个线圈的每匝线圈产生的感应电动势相同，设原线圈的匝数为n1，副线圈的匝数是n2，穿过铁芯的磁通量是Φ，那么原副线圈能产生的感应电路分别是

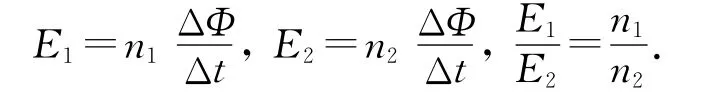
在原线圈中，感应电动势E1起着阻碍电流变化的作用，跟加在原线圈两端电压U1的作用相反，是反电动势，原线圈的电阻很小，如果略去不计，则有U1=E1，副线圈相当于一个电源，感生电动势E2相当于电源电动势，副线圈的电阻也很小，如果略去不计，副线圈相当于无内阻的电源，因而副线圈的端电压U2等于感应电动势.因此得到

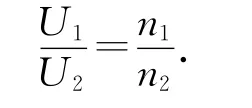
4.2 对变压器工作原理的再分析

（1）进一步树立法拉第电磁感应定律的正确性.变压器是利用了互感的原理.原线圈、副线圈中产生的感应电动势均遵循

（2）副线圈中感应电动势产生的磁通量与原线圈反电动势产生的磁通量大小相同、方向相反，铁芯中的磁通量是由励磁电流决定，无论是空载还是正常工作都遵守这一规律.[2]

（3）由于励磁电流较小，变压器正常工作时原线圈中电流远大于励磁电流，原线圈中的电流是由副线圈中的电流决定，原线圈中除去励磁电流外产生的磁通量与副线圈中电流产生的磁通量相互抵消，感应电动势大小是由励磁电流产生的磁通量决定.

（4）根据变压器的原理，导体棒电动势的均匀增加只能导致原线圈、副线圈中产生的感应电动势增加，不表示铁芯中的磁通量均匀增加，由于原线圈的反电动势要趋于导体棒的电动势，因而铁芯中的磁通量的变化率事实上在均匀增加，副线圈上产生的电动势也相应地均匀增加，这样就满足了

5 结论与启示

原题中第（2）小问的解析是错误的，变压器副线圈上的电压应该是同步均匀增加.在教学中要回归本真，首先要考虑学生的基础和可行的学习目标，其次要考虑学科知识的生长规律，再次是学生的认知规律、习惯要特别关注.教学中不能得过且过，没有科学依据地任意下结论，一旦这样会让学生形成虚假概念、错误认知方法和不严谨的科学思维，这对后续的学习危害是非常严重的，学生后期更正要花大量的精力且不一定有好的效果，不利于学生科学思维的形成和核心素养的发展.