时滞作用下忆阻耦合FHN-ML神经元模型的分岔分析

张美娇，张建刚，魏立祥，南梦冉

兰州交通大学数理学院，甘肃兰州730070

前言

神经元是生物神经系统结构和功能的基本单位。神经系统中各类神经元相互协作，以不同放电模式实现对信息的编码、传递和解码。1952年，Hodgkin 等［1］在乌贼神经突触生理实验中提出Hodgkin-Huxley（H-H）神经元模型，以便精确地描述神经元放电模式。1961年，FitzHugh［2］通过引入恢复变量来表示膜电压的慢变过程，建立了二维FitzHugh-Nagumo（FHN）模型。1975年，Bautin［3］对FHN 模型做了拓扑和定性分析，观察到了大量的非线性现象。随后有关耦合FHN 神经元网络动力学的研究报道不断涌现［4-6］。

由于各类神经元之间信号处理与传递的过程存在时间延迟，激发了学者们对时滞耦合神经元的理论研究。Wang 等［7］利用稳定性和分岔理论研究了具有时滞效应的两个相同HR 神经元突触耦合的平衡分岔、折叠分岔和Hopf分岔的渐近稳定性。Mao［8］建立具有延迟耦合的环形FHN 神经元模型，分析神经网络的稳定性，并通过数值仿真说明耦合强度和时滞在神经网络动力学中都发挥着重要的作用。洪懿暄等［9］研究了时滞神经元网络在外部电流刺激下的耦合同步问题，并通过构造合适的Lyapunov-Krasovskii 自适应律得到了耦合时滞网络的同步条件。

为了更好地模拟神经元间的突触结构，Strukov等［10］证实了一种有记忆功能的非线性电阻元件（忆阻器）的存在。Zhang 等［11］探讨了初始条件对忆阻耦合FHN 神经元模型混沌振荡以及同步过程的影响。杨腾云等［12］利用快慢动力学讨论了含有磁控忆阻器的ML 神经元模型的分岔行为，并描述了系统随磁通反馈系数变化时的放电模式。

本文拟基于ML 和FHN 神经元模型，通过引入磁控忆阻器和时滞项，建立时滞作用下忆阻耦合FHN-ML神经元模型，研究不同时滞作用下该系统的动力学行为。首先，拟利用Routh-Hurwitz 判据和Hopf分岔定理证明系统平衡点稳定性及Hopf分岔的存在性。其次，拟利用范式理论和中心流形定理进一步证明系统的分岔方向及周期解的稳定性。最后，利用MATLAB 软件绘制在不同时滞作用下系统的双参周期分岔图及单参周期分岔图，分析不同时滞对该系统放电模式的影响。

1 模型描述

为了解各类神经元之间的信息传递过程，本文基于ML 和FHN 神经元模型，考虑其在电磁辐射作用下会产生电磁感应现象，因此引入磁控忆阻器使得感应电流通过反馈来调节神经元的膜电位［13］；在信息处理过程中，考虑相邻神经元之间信号传递存在时间延迟，通过在耦合FHN-ML 神经元模型中引入时滞项，从而建立时滞作用下忆阻耦合FHN-ML神经元模型。该系统如下：

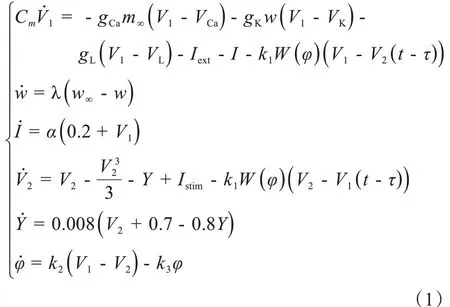
2 平衡点稳定性及Hopf分岔的存在性

其中，h1r1(r1= 1,2,3,4,5,6)，h2r2(r2= 1,2,3,4)，h3r3(r3= 1,2,3)分别表示特征方程相应的系数。

本文将τ分两种情形讨论［15］。情形一：当τ= 0时，式（3）可以写成：

其中，ρ11=h11，ρ12=h12+h21，ρ13=h13+h22+h31，ρ14=h14+h23+h32，ρ15=h15+h24+h33，ρ16=h16。

由Routh-Hurwitz［16］判据可知，若式（4）的所有系数主行列式及顺序主子式全部大于0，则所有的根都具有负实部，即得到结论：系统（1）的平衡点E*(V1*,w*,I*,V2*,Y*,φ*)对于τ是局部渐近稳定的。

情形二：当τ> 0 时，式（3）左右两边同时乘eλτ即写成：

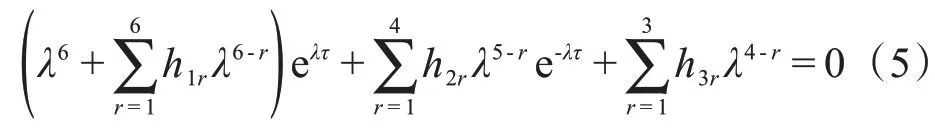
假设λ=iω(ω> 0)是式（5）的根，分离实部与虚部后可得：

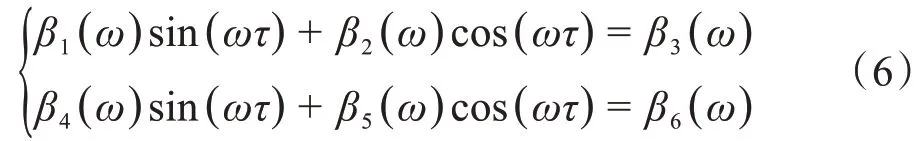
其 中 ，β1(ω)=(h12-h21)ω4+(h23-h14)ω2-ω6+h16，β2(ω)=h11ω5-(h13+h22)ω3+(h15+h24)ω，β3(ω)=h31ω3-h33ω，β4(ω)=(h13-h22)ω3+(h24-h15)ω-h11ω5，β5(ω)=(h12+h21)ω4-(h14+h23)ω2-ω6+h16，β6(ω)=h32ω2。即可得关于ω的方程：

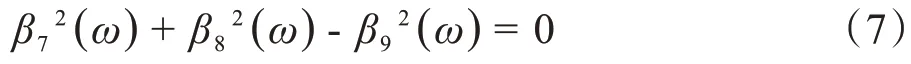
其中，β7=β3β5-β2β6，β8=β1β6-β3β4，β9(ω)=β1β5-β2β4，如果式（7）有一个正根ω*，即得：τ*=，式（5）对τ求导，假设λ=iω*，化简后即得：

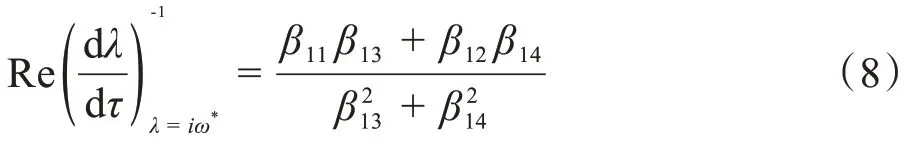
其中，

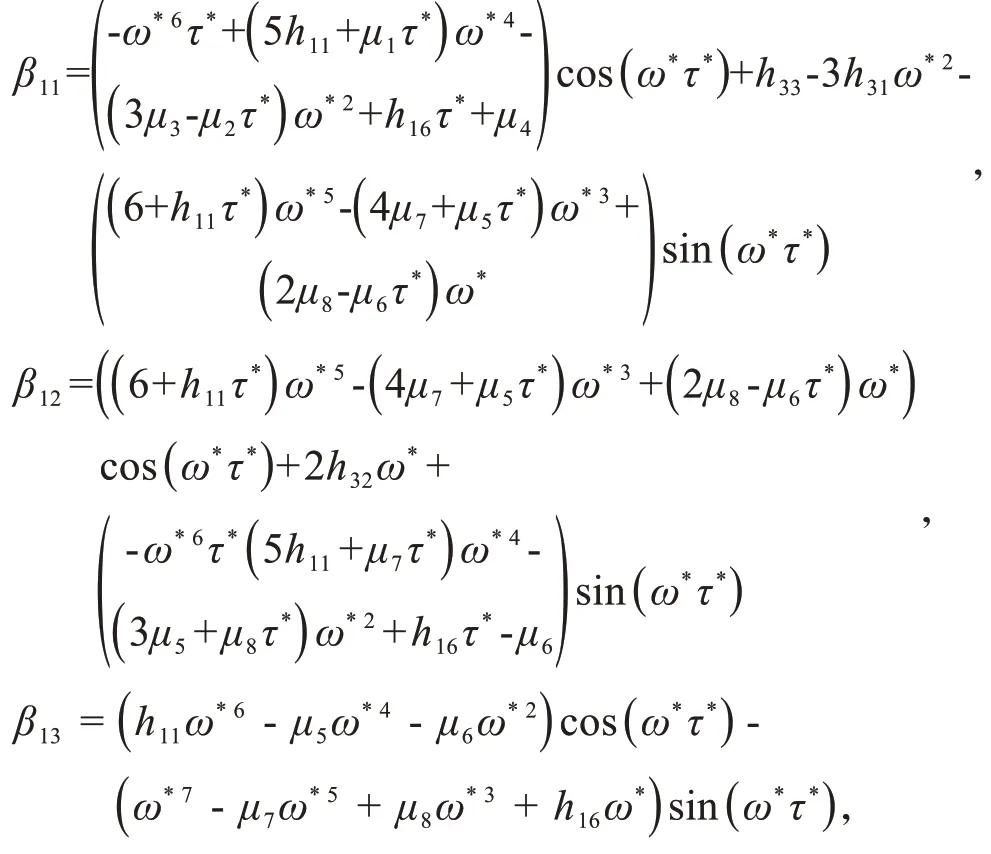
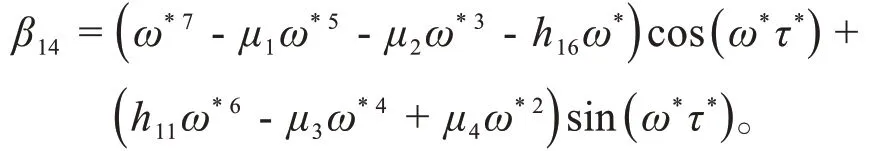
当β11β13+β12β14≠0 时，，由Hopf分岔定理［17］即得到结论：当τ∈[0,τ*)时，平衡点E*(V1*,w*,I*,V2*,Y*,φ*)是局部渐近稳定的；当τ>τ*时，平衡点E*(V1*,w*,I*,V2*,Y*,φ*)是不稳定的；当τ=τ*时，系统（1）在平衡点E*(V1*,w*,I*,V2*,Y*,φ*)处存在Hopf分岔。

3 分岔方向及周期解的稳定性

在前面小节中，证明了当τ=τ*时，系统（1）在平衡点E*(V1*,w*,I*,V2*,Y*,φ*)处存在Hopf 分岔。下面利用范式理论［18］和中心流形定理进一步证明分岔方向及周期解的稳定性。将系统（1）引入变换：设，即可得到泛函微分方程组：

其中，x(t)=(x1(t),x2(t),x3(t),x4(t),x5(t),x6(t))T，Lϑ和f分别表示线性和非线性算子，同时满足：

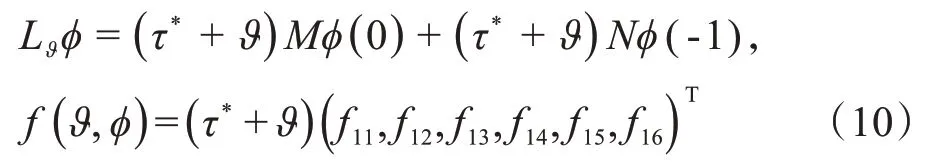
其中，φ=(φ1,φ2,φ3,φ4,φ5,φ6)T∈C，f1i(i= 1,2,3,4,5,6)分别表示非线性项。

根据Riesz 定理［19］，存在有界变差函数η(θ,ϑ)，θ∈[-1,0]使得：L选取η(θ,ϑ)= (τ*+ϑ)Mδ(θ)- (τ*+ϑ)Nδ(θ+ 1)，定义：

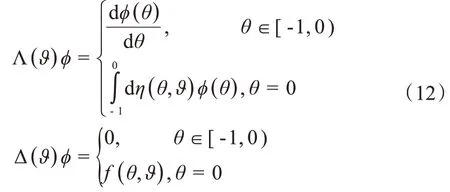
即式（9）等价于：

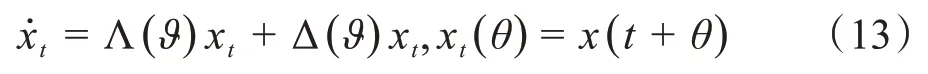
对于Ψ ∈C1([0,1],(R6)*)，η(θ)=η(θ,0)，定义Λ*和双线性内积如下所示：

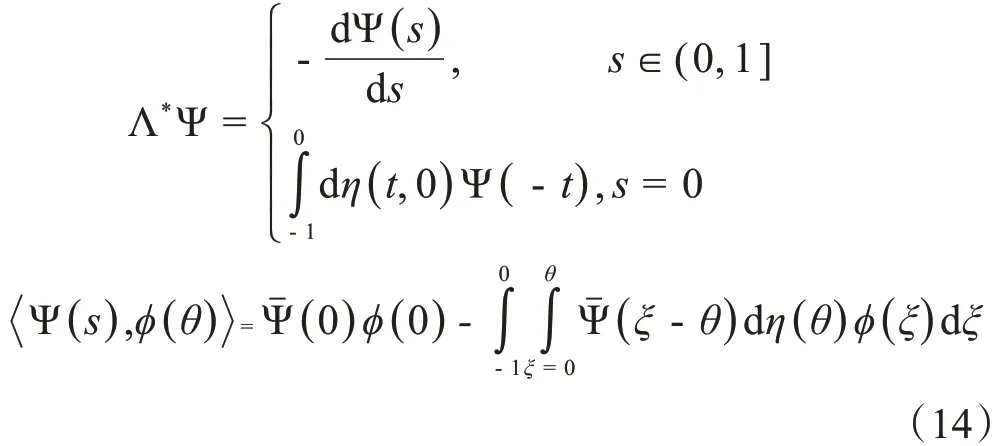
其中，Λ*是Λ(0)的伴随线性算子，显然，±iω*τ*是Λ*的特征根。设Λ(0)q(θ)=iω*τ*q(θ)，Λ*(0)q*(s)=-iω*τ*q*(s)，同时令q(θ)=(1,ν1,ν2,ν3,ν4,ν5)Teiω*τ*θ，q*(s)=G(1,ν*1,ν*2,ν*3,ν*4,ν*5)Teiω*τ*s，即有：

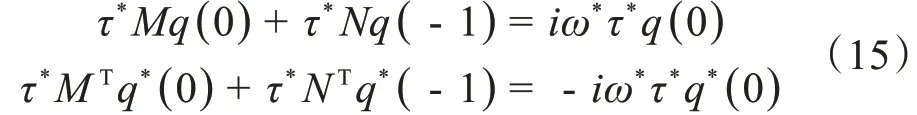
由式（15）可求得νr,ν*r(r= 1,2,3,4,5)的表达式，由式（14）可求得：

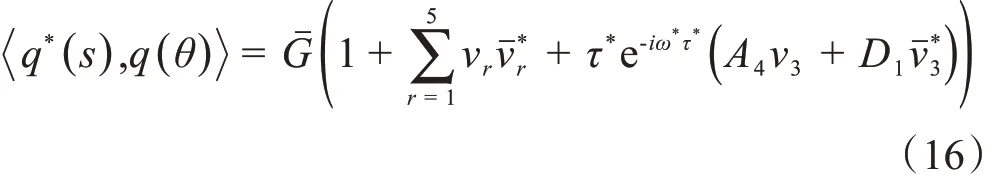
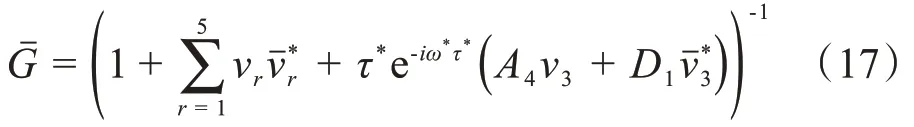
依据Hassard 方法［20］，即可计算出当ϑ= 0 时，中心流形C0的坐标g02、g11、g20、g21，并且W20(θ)=

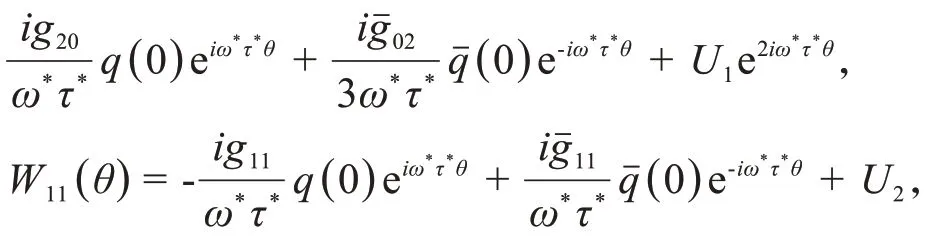
其中：

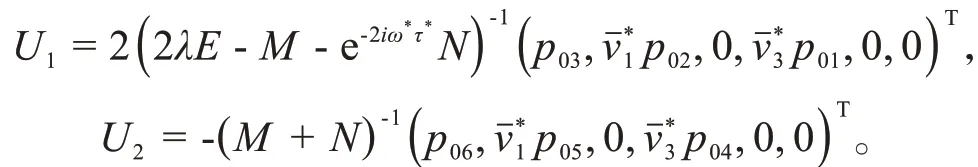
即可得到下列值：

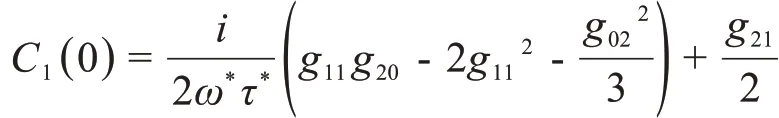
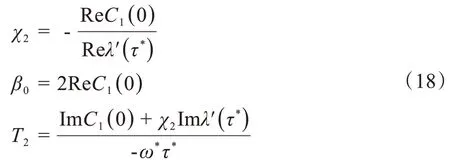
以上参数中，χ2决定Hopf分岔的方向：如果χ2>0，Hopf分岔是超临界分岔；如果χ2<0，Hopf分岔是亚临界分岔；且τ>τ*(τ<τ*)时分岔周期解存在；β0决定了分岔周期解的稳定性：如果β0<0(β0>0)，分岔周期解是稳定的（不稳定的）；T2决定了分岔周期解的周期：如果T2>0(T2<0)，分岔周期是递增的（递减的）。

4 数值模拟

在数值计算过程中，系统参数具有高度的敏感性，即系统（1）的膜电位会随着参数的变化呈现出不同的放电模式。本文所研究的膜电位为ML神经元膜电位V1。为了得到更为精确的研究结果，以双参数Vk和γ作为变量，取系统其它各参数值分别为：Cm= 1μF/cm2，gCa= 1.2 ms/cm2，gK= 2.0 ms/cm2，gL= 0.5 ms/cm2，VCa= 1mV，VL= -0.55 mV，Iext= 0 mA/cm2，a= 0.5，b=0.5，α=1.3，k1=0.4，k2=0.58，k3=0.5，m11=-0.01mV，m22= 0.15 mV，m33= 0.1mV，m44= 1.55 mV。在双参数平面Vk∈[1,2.6 ]，γ∈[0.062,0.068 ]上，绘制不同时滞作用下相应的双参周期分岔图（图1），图1中不同的颜色对应着不同的周期簇放电态，右边颜色栏的数值对应着相应的周期簇放电态（如数字5对应周期5簇放电态，数字10对应周期10簇放电态，白色区域对应大于或等于20的周期簇放电态或者混沌放电态）。

当Vk∈[1.00,1.65 ]，γ∈[0.062,0.0638 ]时，观察图1a 发现，随着Vk的逐渐增大，膜电位由周期2 簇放电态通过加周期2分岔进入周期4,6,8…通向“梳状”的混沌放电区域。图1b 与图1a 相比，加周期分岔的周期数减少，此现象在图1c 中更为显著，其直接由周期2簇放电态进入混沌态，加周期分岔消失。这说明时滞τ的改变影响了系统（1）的放电模式。

当Vk∈[1.65,2.60 ]，γ∈[0.062,0.068 ]时，观察图1a中黑线从右上到左下的走势发现，膜电位首先由混沌态进入周期8窗口，再通过逆倍周期分岔［21］进入周期4窗口，之后通过加周期分岔进入大范围的周期5窗口，随后通过倍周期分岔再次通向混沌态，接着继续进入周期7窗口同样经过倍周期分岔又一次进入混沌态…这样一直重复着前面的放电模式，最终趋向于周期2簇放电态。同时，当倍周期分岔与混沌交替出现时，每次混沌放电后的周期要比混沌放电前大2，当周期数不断变大时，相应的颜色带逐渐变窄，且混沌窗口也逐渐变小。此外图1b和图1c也存在类似的现象。而图1b与图1a相比，混沌放电区域减小，其图1c则以周期放电为主。图1b与图1a相比，原本周期7、9、11、13、15窗口分别有8、10、12、14、16窗口混入，而图1c与图1b相比，混入的窗口明显增大，说明时滞τ使系统（1）本该在上一周期的放电模式延迟至下一周期，从而形成了固定颜色带中有多种颜色混合的现象，且时滞τ越大，混入的颜色带区域越大。

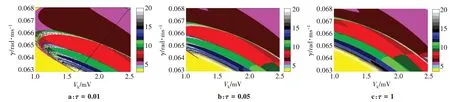
图1 膜电位在不同时滞τ下的双参周期分岔图Fig.1 Two-parameter periodic bifurcation diagrams of membrane potential with different time delays τ

保持参数Vk= 1.6 不变，绘制不同时滞作用下以γ为单参的峰峰间期（ISI）分岔图（图2）。观察图2a发现，随着参数γ的减小，膜电位由周期5窗口经倍周期分岔通向混沌态，之后进入周期7窗口经倍周期分岔又一次通向混沌态，随后进入周期9窗口经倍周期分岔再次通向混沌态…这样一直重复着前面的放电模式，最终趋向于无混沌的周期放电。而图2b 与图2a 相比，通向的混沌区域减小，同时每次出现混沌放电时，γ的值增大，其图2c 更大程度地反映出这一现象。这表明随着时滞τ不同程度的增大，放电模式出现了不同程度的延迟。

图2 膜电位在不同时滞τ下的单参分岔图Fig.2 Single-parameter bifurcation diagrams of membrane potential with different time delays τ

5 结束语

本文基于ML 和FHN 神经元模型，构建时滞作用下忆阻耦合FHN-ML 神经元模型，分析该神经元系统在不同时滞作用下的动力学行为。利用Routh-Hurwitz 判据和Hopf 分岔定理证明FHN-ML 神经元系统的平衡点对于τ∈[0,τ*) 是局部渐近稳定的；对于τ>τ*是不稳定的；当τ=τ*时，FHN-ML 神经元系统在平衡点处存在Hopf分岔。利用范式理论和中心流形定理进一步证明χ2决定Hopf 分岔的方向；β0决定分岔周期解的稳定性；T2决定分岔周期解的周期。通过绘制在不同时滞作用下以反转电压Vk和电流频率γ为双参的周期分岔图发现，随着时滞τ的增大，FHN-ML神经元系统膜电位混沌放电区域减小，加周期分岔的周期数减小。同时由于时滞τ使本该在上一周期的放电模式延迟至下一周期，出现了固定周期窗口混入了其他周期窗口的现象，且时滞τ越大，混入的周期窗口越大。通过绘制在不同时滞作用下以电流频率γ为单参的峰峰间期（ISI）分岔图发现，FHN-ML 神经元系统混沌放电区域随着时滞τ的增大而减小，这与上述放电模式的分析结果相似，同时放电模式也会随着时滞τ的增大而产生延迟现象，且在不同时滞的影响下，产生不同程度的延迟。

综上所述，时滞是影响FHN-ML 神经元系统放电模式的重要因素，所得研究成果对在电磁辐射作用下具有延迟效应的耦合神经元网络动力学的研究具有极大的参考价值。