撒克逊碗在液体中下沉运动的理论与实验研究

◇咸阳师范学院物理与电子工程学院 李 君 华雪侠 邱少琴 张妮妮 张凯峰 高 燕

本文利用Tracker软件的自动追踪功能，对撒克逊碗在液体中下沉运动进行分析，得到撒克逊碗运动的数据及图像。在考虑粘性力与突扩管道的流动损失的情况下，从浮力，流动阻力，流体中黏性力等方面对撒克逊碗分析受力，在用孔口出流，伯努力方程物理关系构成可解的运动微分方程组分析研究撒克逊碗下沉运动原理，利用Tracker软件捕捉到的数据，通过控制变量法进行定量分析撒克逊碗下沉时间的影响因素，与理论分析计算出来的数据进行对比分析，从而给出具体求解不同撒克逊碗在液体中的下沉时间。

一个底部有洞的碗放在水中会下沉，撒克逊人用这个装置来计时，所以底部有洞的碗称为撒克逊碗。撒克逊碗在液体中下沉运动可以看作竖直方向的阻尼振动，在考虑粘性力与突扩管道的流动损失的情况下，通过对撒克逊碗在液体下沉运动的受力分析以及撒克逊碗小洞的伯努利方程流动损失修正进行分析，列出撒克逊碗在液体下沉的运动方程，并且通过实验的初始条件进行MATLAB数值求解得出撒克逊碗下沉时间及运动轨迹。在利用Tracker 软件通过建立坐标轴、定标杆，结合形象直观的图像、表格进行定量分析准确地追踪撒克逊碗在液体中下沉运动中的位置，并得到其运动的相关数据。对比分析理论数据与实验数据分析理论计算得可靠性，从而具体求解不同撒克逊碗在液体中的下沉时间。

1 撒克逊碗下沉过程的实验原理分析

以最理想的状态分析。假设水槽足够大，撒克逊碗进行下沉的过程中，水面高度不发生变化。流体在撒克逊碗小洞中运动状态忽略，以撒克逊碗小洞上方的速度为洞中水流速。假设撒克逊碗底面的水流速为0，局部损失为静压下的。撒克逊碗质心与洞的位置都集中在碗中心，入水时撒克逊碗与水面无倾。

1.1 撒克逊碗进入液体的的运动状态分析[1-2]

撒克逊碗的小洞上下受压差作用力，使液体不断压入撒克逊碗中，壁面附近的流体受粘性作用不断减速，无粘核心区的不断加速度。这个小孔进水运动状态与速度形式比较复杂。但对于不可压流体，等截面，可知任一截面上的平均流速度不变。

液体进小洞上方运动形式，如图1所示，一侧先进水受一个力矩作用下倾斜，在重力作用下另一侧在进水，从而进入以上以下的周期运动下沉。

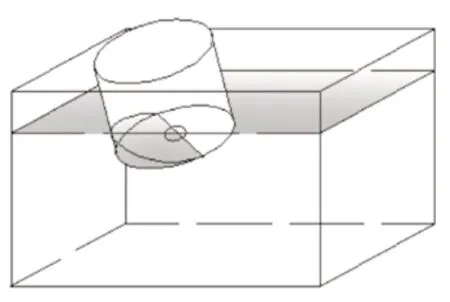
图1 液体进孔上方运动形式图

当碗完全进入水后，由于撒克逊碗本身的重力影响下，进水液面高度永远小于液面高度，水最后会灌入撒克逊碗中，使撒克逊碗的下落的速度更大。

1.2 撒克逊碗进入液体的条件

撒克逊碗在液体中的模型及参数以及下沉运动过程图如图2和图 3所示。

图2 撒克逊碗模型参数图

图3 撒克逊碗在液体中下沉运动原理图

撒克逊碗能否在液体中下沉运动取诀于撒克逊碗的重力能否大于小洞所产生表面张力与液体浮力，撒克逊碗的重力大于时，撒克逊碗进行下沉运动，撒克逊碗的重力小于时，撒克逊碗在液体表面悬浮不发生运动。

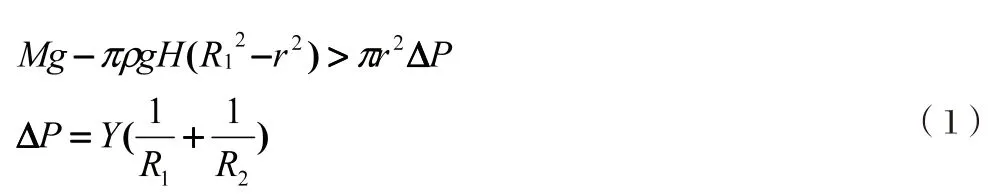
1.3 碗水中下沉撒克逊过程力学运动模型

首先对撒克逊碗受力分析以撒克逊碗为坐标系，对撒克逊碗进行受力分析，以竖直向下为正方向设撒克逊碗在液面速度，底部在液面加速度

由牛顿第二定律可得：

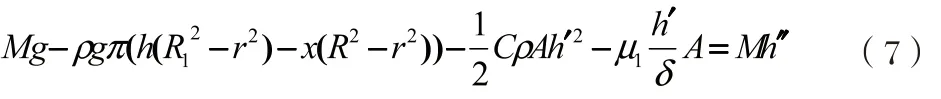
构建速度微分方程，设撒克逊碗底部在进水液面速度为由流体连续方程

由假设可知碗底下方的水静止的，流速为0，使用符合伯努利方程可得：

在缓慢下落的前提下，碗的下沉加速度远远小于重力加速度得：

突扩管道的流动损失：当流体从小尺寸管道突然进入大尺寸的管道时，会发生突变式分离，进而产生大量的损失[2]。

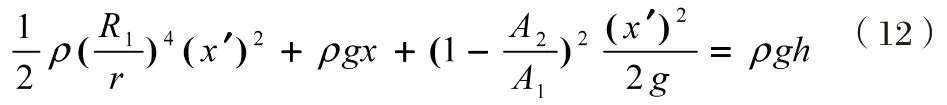
可得撒克逊碗下沉运动微分方程组为：

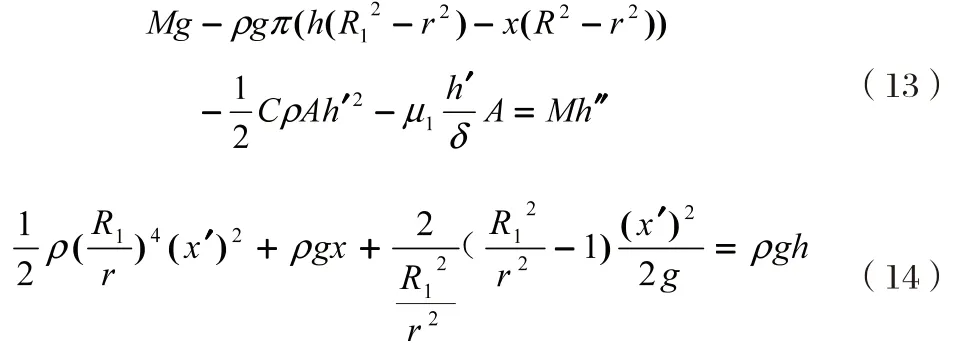
然后利用MATLAB软件进行数值求解。

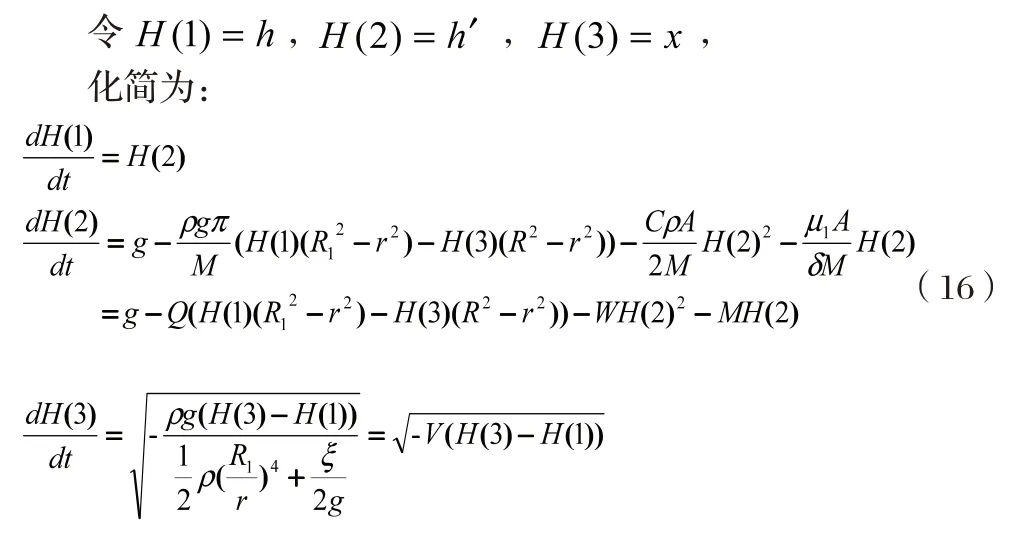
在第2部分数据分析中通过解微分方程组，求解出撒克逊碗的运动状态与碗中的水的运动状态，并与实验作对比。

2 实验操作及数据处理

为了方便捕捉的撒克逊碗在液体中下沉运动，在撒克逊碗下端部位用马克笔画画上黑点作为质点对象。将撒克逊碗从入液体高度位置平衡释放，让撒克逊碗开始自由的做下沉运动，拍摄视频。将拍摄的视频导入Tracker，建立适当的坐标轴，选取合适的参照物，确定水面深度为定标杆长度，本实验以撒克逊碗自身为参照物，设置定标杆长度为0.48m。创建用马克笔画画上黑点作为质点，在视频中确定好质点对象，点击搜索，软件将自动搜索质点对象运动过程的位置时间图像和速度时间图像，并描绘相应的图像，如图4、图5、图6、图7。

图4 时位移时间 h-t 图

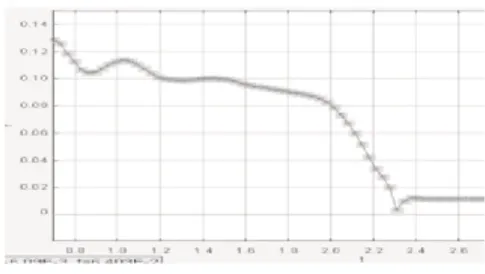
图5 时位移时间 H-t图

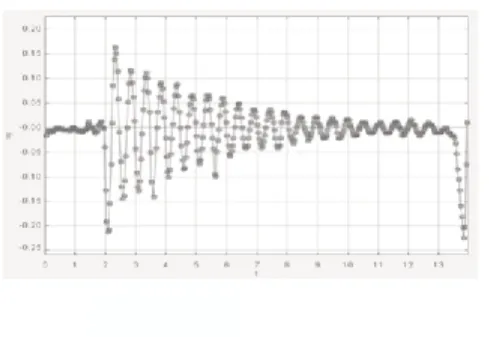
图6 时速度时间v-t图

图7 时速度时间v-t图

本文通过控制变量法由多个不同大小的撒克逊碗进行初步实验，我们发现对撒克逊碗下沉时间的影响因素为撒克逊碗底部半径，撒克逊碗底部孔半径，撒克逊碗高度，撒克逊碗质量。

（1）控制其他条件不变，改变碗底部孔半径大小，如图8所示。在质量为66 g，高度为4.8 cm，底部半径为4.35cm(R)的撒克逊碗中进行实验可得实验数据，再由数值求解理论数据为：

图8 不同撒克逊碗底部孔半径

（4）在其他条件相同下，改变撒克逊碗质量，如表4所示是在高度为8.98 cm，底部孔半径为r=0.77 cm，底部半径为R=4.35 cm的撒克逊碗中进行实验可得实验数据，再由数值求解理论数据为：

表4 不同撒克逊碗质量下沉与实验时间理论时间表

由数据分析图9和表1可看出来对于不同孔半径的碗的波动曲线不同，运动的行式与阻尼运动行式相近。对于孔半径小的，碗底半径大的所产生的振动次数比较多，下沉的也比较慢；对于孔半径大的，碗底半径小的所产生的振动次比较少，下沉快。随着碗的底部孔的变大，碗下落时间逐渐变小，随着孔的变大振动的次数不断的变少。

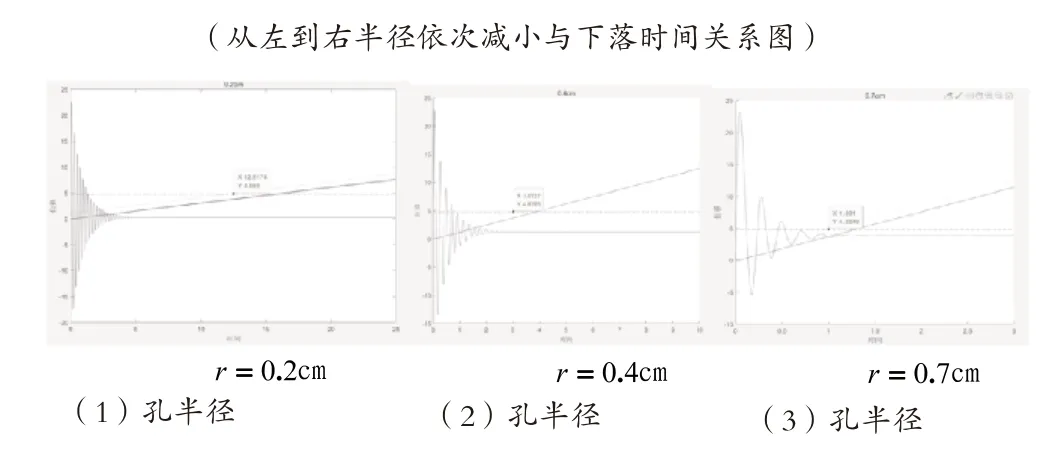
图9 不同孔半径下沉曲线对比图

表1 不同撒克逊碗底部孔半径与下沉实验时间理论时间表

（2）控制其他条件不变，改变撒克逊碗底部半径R。在质量为73 g，底部孔半径R为0.3 cm，高度为4.9 cm的撒克逊碗中进行实验可得实验数据，在由数值求解理论数据如表2和图10为：

表2 不同撒克逊碗底部半径与下沉实验时间理论时间表

图10 碗底部半径半径不同的下沉曲线对比图

随着碗的底部面积变大，碗下落时间逐渐变长。当面积达到一定时，碗无法进入水中，在水表浮着，随着底部半径的变大振动的次数不断的变多。

（3）其他条件相同下，控制撒克逊碗高度不同。在质量为60.3 g，底部孔半径为0.38cm(R)，底部半径为3.15cm(R)的撒克逊碗中进行实验可得实验数据，再由数值求解理论数据如表3和随着的高度变大，碗下落时间逐渐变长。图11所示：

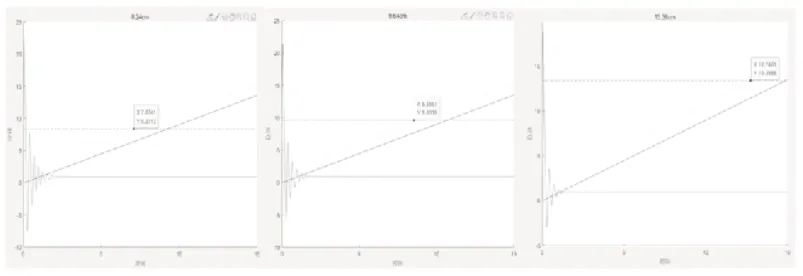
图11 撒克逊碗高度8.24；9.64；13.38cm下沉曲线对比图

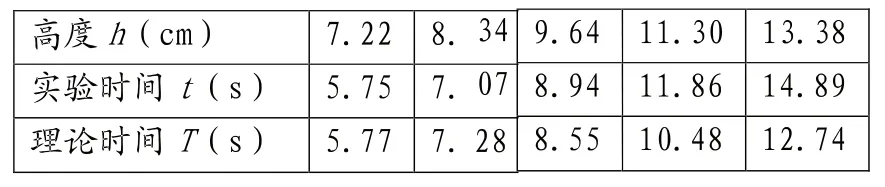
表3 不同撒克逊碗高度下沉与实验时间理论时间表

由于改变质量比较困难，实验数据比较不精确没有呈现出来，但观察可得随着质量的变大，碗下落时间逐渐变短，理论数据也是如此反应的。

3 结论

综上所述，我们从撒克逊碗在液体下沉运动的受力分析与撒克逊碗小洞的伯努利方程流动损失修正入手，建立起了物理意义明显的理论方程，通过数值模拟和相关实验验证了方程组式的正确性，发现对撒克逊碗下沉时间的影响因素之间的关系，分析了随着孔的变大振动的次数不断的变少，随着底部半径的变大振动的次数不断的变多等各各因素对下沉曲线的影响，并且可以计算出不同撒克逊碗下沉时间的确定数值。但由于撒克逊碗在液体下沉运动系统的复杂性，我们寄希望于未来可以更好的算法解决这个技术问题。