RC梁正截面受弯破坏数值分析

郭星辰，张耀文，王伟峰，伊力夏提·阿不都西库尔

（1. 中国建筑第七工程局有限公司，河南 郑州 450000；2. 新疆大学建筑工程学院，新疆 乌鲁木齐 830047）

钢筋混凝土梁是由钢筋与混凝土组合在一起的承重构件且在桥梁、房屋建筑等应用极为广泛。相关规范已经日趋成熟[1-4]。其原因是钢筋的抗拉能力与混凝土的抗压能力均可得到充分发挥，共同提高梁的受弯承载力。ABAQUS 是一套功能强大的工程模拟软件，它拥有一个可模拟任意几何形状的单元库和各种类型的材料模型库，可以模拟典型的工程材料的性能，其中就包括钢筋混凝土，经常被业内人士用于解决结构（应力/位移）问题。为了对钢筋混凝土梁的破坏及力学性能变化有更加深刻的认识，通过 ABAQUS 有限元分析软件对三种配筋梁进行受弯模拟试验，基于后处理提取相关数据，为钢筋混凝土梁相关课程提供一定解析。

1 梁构件加载模式及配筋方式

模型试验方式依据文献 [5]，梁长度取 2500mm，截面尺寸 b×h 为 200mm×300mm，混凝土强度为C30，箍筋与纵向受拉钢筋均为 HRB440 级，混凝土保护层厚度取 25mm。梁模型加载图如图 1。依照梁截面配筋计算得出配筋图见图 2。

图1 加载示意图

图2 配筋图

配筋计算：

剪跨比取为 3

则 Av=96mm2，箍筋选择 A8＠150，

Asv=42×3.14×2=100mm2＞96mm2，满足梁在受剪下要求。

少筋梁的配筋方式为受拉纵筋 2Φ6：

超筋梁受拉钢筋以 2Φ28 方式布置：

适筋梁采用 2Φ20 方式布筋：

2 有限元模型建立及计算

运用 ABAQUS 有限元分析软件对适筋梁、少筋梁及超筋梁的破坏模式及荷载位移曲线分析。混凝土采用内置的混凝土塑性损伤模型。混凝土塑性损伤模型是用来分析混凝土结构在循环和动力荷载下提供的一个普通分析模型，能较好地反映混凝土材料的退化性能，在混凝土中反应的失效机制是拉力作用下的开裂失效和压力作用下的压碎。混凝土本构曲线依照 GB 50010—2010《混凝土结构设计规范》[6]中提出的曲线，受压及受拉本构曲线见图 3 (a)、图 3 (b)。混凝土采用三维八节点实体单元，这样能够更加直观了解裂缝发展情况及梁整体破坏规律。钢筋采用 HRB440 级，选取桁架单元，因为梁单元可承受拉压弯曲载荷，而桁架单元只承受轴向力是比较简单的单元结构，只要能算出内力，其应力应变立马可以求出，所以采用桁架单元。赋予截面尺寸，钢筋本构[7]曲线见图 3 (c)。由于进行梁的两点受弯试验，为忽略垫板的变形，给到垫板足够大弹性模量[8]。混凝土塑性相关参数如表 1。

图3 材料本构曲线

表1 混凝土塑性参数

混凝土与垫板之间接触设定为绑定，钢筋笼内嵌入混凝土中，支座以简支方式支撑梁，垫板各表面设置耦合点。边界条件 Rp3 约束 U1=U2=0，UR1=UR2=UR3=0，Rp4 约束 U1=U2=0，UR1=UR2=0。在上垫板外表面施加竖向荷载[9]，网格划分 40mm 见图 4 所示。

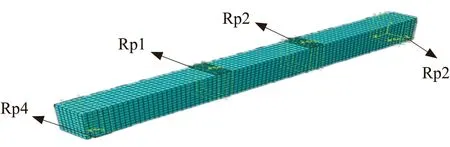
图4 网格划分

3 模型试验结果与分析

3.1 破坏模式

分别对三种配筋梁进行两点压弯模拟试验，以ABAQUS 输出 PEEQ（受压等效塑性应变）及 PEEQT（受拉等效塑性应变）来模拟裂缝的产生及发展。三种配筋梁的 PEEQ 及 PEEQT 云图是应变分布动态图，颜色对应大小，见图 5、图 6 与图 7。从 PEEQ 云图上看，适筋梁及超筋梁受压区混凝土均已破坏，而少筋梁受压区混凝土近乎完好无损。就 PEEQT 云图来看，少筋梁受拉区混凝土破坏较为严重且裂缝集中产生在受弯荷载两点之间，从动态云图中发现，裂缝产生及向上发展较为迅速，究其原因是混凝土抗拉强度低，梁中配置钢筋过少，导致梁构件整体承受拉应力的能力过小，破坏模式近乎为斜拉破坏。结合动态裂缝云图观察适筋梁的破坏过程为受拉区混凝土边缘率先开裂，之后裂缝产生区域缓慢延伸至支座两点，之后受压区混凝土逐渐被压碎，表现出塑性破坏特点，可以认为梁中的拉压应力维持在一个相对均衡的情况，既发挥了钢筋的抗拉能力，有突出混凝土的抗压能力，呈现出剪压破坏。超筋梁就 PEEQ 云图主要破坏集中在受压区混凝土被压碎，受拉区混凝土没有产生明显裂缝，由于配筋率超过界限配筋率，梁中的拉应力大于压应力，表现为斜压破坏。

图5 超筋梁

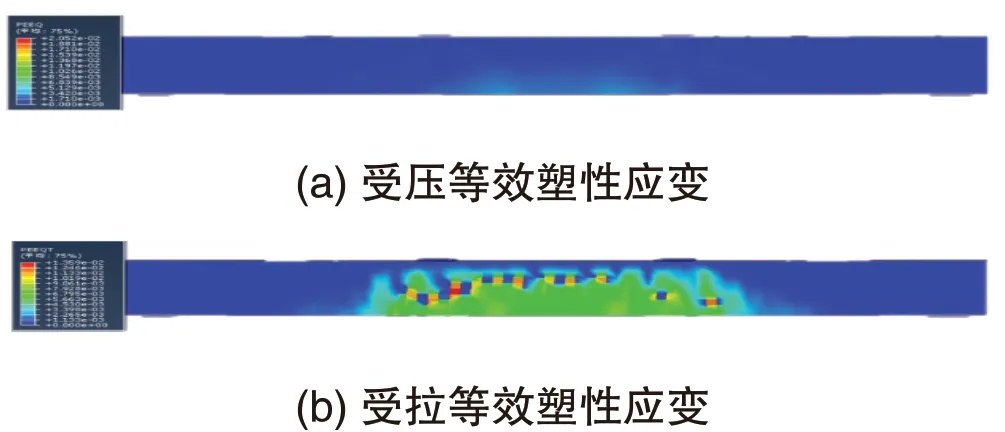
图6 少筋梁

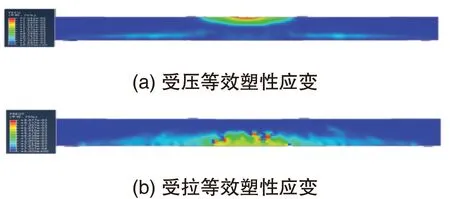
图7 适筋梁

3.2 梁荷载位移曲线

三种配筋梁的荷载位移曲线见图 8。相比于试验，少筋梁数值模拟破坏近乎为 2 阶段，开始加载，二者共同承受荷载，近乎为线弹性，达到峰值拉应力后，混凝土开裂，承载力降低，但 ABAQUS 中混凝土属连续实体单元，即使破坏仍然具有一定承载能力，钢筋进入强化段，承载力略微提升后下降，与实际试验有一定出入。适筋梁分为 3 个阶段：第一阶段混凝土与钢筋共同承受荷载，但主要承受承载力的是混凝土，表现为线弹性阶段；第二阶段混凝土抗拉能力骤减，转移至钢筋承受拉应力，刚度有明显退化，钢筋的拉应力提升速率加快，梁底受拉区裂缝随之发展；第三阶段，受拉钢筋屈服，此时的受压区段混凝土并未达到峰值压应力，且压应力增速缓慢，表现出来近乎为一条直线，达到极限压应力之后，梁丧失承载力。超筋梁受拉区混凝土开裂瞬间曲线稍有转折，此时刚度退化不明显，随后曲线继续上升，待到受压区混凝土被压碎，钢筋未屈服，属脆性破坏。

图8 梁荷载位移曲线图

3.3 应力云图分析

应力云图是指应力的分布动态图，颜色的不同代表着应力的大小，可以直观地观察应力分布的全过程，有利于分析破坏机理。

3.3.1 混凝土应力云图

混凝土应力云图见图 9。可以看出少筋梁压应力面积较小且集中在纯弯段即中间段，最大压应力值为10MPa，未达到峰值压应力，混凝土的抗压性能未充分发挥。适筋梁加载点与支座之间形成“弓”形压应力区且纯弯段混凝土压应力充分发挥。超筋梁混凝土压应力区域面积过大，但纯弯段混凝土压应力未有明显提高。

图9 混凝土 MiSe 应力云图

3.3.2 钢筋应力云图

钢筋应力云图见图 10。可以发现适筋梁与超筋梁纵向受拉钢筋都已屈服，但相较于二者，适筋梁纵向受拉钢筋受力较为充分，由中部延伸至支座边缘，且配置的箍筋产生了良好的抗剪效果，致使梁有良好的塑性变形能力。少筋梁受拉钢筋受力范围多在纯弯段。就超筋梁，纵向受拉钢筋受力范围与适筋梁基本一致，但箍筋的抗剪能力未得到发挥，究其原因是梁内压应力小于拉应力致使的梁自身变形过小。

图10 钢筋 MiSe 应力云图

3.4 混凝土应力、应变与时间步关系

以纯弯段混凝土受拉区与受压区应力、应变变化规律评估 RC 梁破坏机理。受拉区混凝土应力、应变与时间步的关系见图 11 与图 12。可以发现三种配筋梁均达到混凝土最大拉应力，此时时间步为 0.012。但下降段差别较大，少筋梁下降至拐点过程，斜率变化较为迅速，而且对应的应变增速较快，说明受拉区混凝土的破坏是一瞬间。而适筋梁下降段到达第一拐点时，斜率相对于少筋梁变得缓慢，可以认为混凝土开裂后，合适的配筋率使得混凝土抵抗受拉破坏的能力提高，出现第一拐点的时间步与钢筋屈服时间步相吻合，随后拉应力出现回升，是由于钢筋屈服后出现强化。混凝土的应变至钢筋屈服后才发展较快。超筋梁到达第一拐点的时间步相比于前两种更加缓慢，说明配筋率高使得受拉区混凝土的抗拉能力提高，受拉钢筋为充分发挥其抗拉能力，混凝土的应变较小。

图11 受拉区混凝土应力曲线

图12 受拉区混凝土应变曲线

受压区混凝土应力、应变与时间步的关系见图 13与图 14。与受拉区混凝土相对应，少筋梁由于拉应力过小，导致受压区混凝土未能发挥其抗压能力，混凝土的应变较小。适筋梁受压区混凝土达到最大压应力同时纵向受拉钢筋提供的拉应力使得受拉区混凝土抗拉能力提高，说明适筋梁既利用了混凝土的抗压能力也利用了钢筋的抗拉能力。超筋梁混凝土压碎先于适筋梁，但与之对应受拉区混凝土未开裂，说明主拉应力过大，受压区混凝土的应变变化迅速。

图13 受压区混凝土应力曲线

图14 受压区混凝土应变曲线

3.5 钢筋应力、应变关系分析

受拉钢筋应力与时间步曲线见图 15 与图 16，可以得出当少筋梁纵向受拉钢筋屈服时对应的时间步为 0.1，适筋梁纵向受拉钢筋屈服时对应的时间步为0.23，超筋梁纵向受拉钢筋未发生屈服。又结合图受拉钢筋应变与时间步曲线图得到少筋梁纵向受拉钢筋在混凝土开裂后，钢筋的应变迅速增大，极限应变为0.022，说明配筋率较低情况下，梁内主拉应力较小，一旦出现受拉损伤，损伤扩展快，梁主体破坏迅速。而适筋梁由于主拉与主压应力处于相对均衡状态，纵向受拉钢筋提供的足够拉应力有效抑制混凝土的受拉开裂，最终受拉钢筋的极限应变为 0.019。对超筋梁来说，纵向受拉钢筋自始至终未屈服，梁破坏后钢筋极限应变仅为 0.0017，究其原因是配筋率大，梁内主拉应力大于其主压应力致使上部混凝土即使被压碎，受拉纵筋也不屈服。

图15 钢筋拉应力曲线

图16 钢筋拉应变曲线

4 结论

（1）数值模拟与试验结果无论是破坏模式还是荷载位移曲线近似度较高，证实了数值模拟的有效性。

（2）整体来看，少筋梁与超筋梁都是由于梁内拉应力与拉应力不均衡导致的脆性破坏，钢筋与混凝土其中之一未发挥其独有特性，工程中应尽量避免。适筋梁的破坏先是混凝土被拉裂，钢筋随后承受主拉应力，裂缝也逐渐蔓延至支座两端，钢筋屈服时混凝土未被压碎，经过一段时间后，受压区混凝土达到极限压应力，混凝土被压碎、梁破坏，有明显的破坏前的征兆，具有延性破坏特征。