基于决策树支持向量机的地表水水质评价研究

周 妍，廖振良，周 灿

（同济大学 环境科学与工程学院，上海 200092）

0 引言

水质评价在本质上是一种多指标、多类别的属性识别的过程，对水资源开发利用、水环境质量监督与保护都有着重要作用，如何使水质评价更加科学、客观、合理是现代环境领域研究的重要课题之一。随着非线性理论、不确定性理论的出现以及计算机技术的快速发展和不断普及，从最初的生物评定法和专家评价法[1]，到现在的单因子评价法[2]、灰色理论法[3]、模糊综合评价法[4-5]等。其中，以单因子为代表的指数评价法虽然计算方法简单，但仅仅采用单一信息的水质评价方法，对于目前复杂多变的水质情况，评价结果往往不能全面的反映出实际的综合水质类别；模糊综合评价法在评价过程中确定效用函数、权重系数等步骤依赖人的主观性，以及指标权重、模糊算子、最大隶属度原则等方面的不确定性，使该方法的评价模式在水质评价领域的通用性有所限制，也对评价结果的可靠性有所影响[6]。因此，如何综合考虑多个水质指标及其浓度成为水质评价的一个难点。

基于统计学习理论的支持向量机（Support Vector Machine,SVM）是近几年迅速发展起来的一种分类模型，为水质评价研究提供了一条新的途径。SVM 是针对分类问题提出的一种机器学习方法[7-8]，不但结构简单，而且在众多数据模型中具有较好的泛化能力，尤其对于小样本的问题，可成功解决神经网络学习过程中“过学习”等问题，同时也能够避免模型陷入局部最优，保证最后得到的极值解是全局最优解[9]。目前，SVM 算法广泛应用在模式识别、时间序列分析[10]、聚类分析[11]等方面。由于水质指标属于一种有限的、非线性的指标，越来越多的专家学者将支持向量机运用到水质评价的领域[12-14]。运用SVM 解决多类问题的分类方法主要有3 种：“一对一”、“一对余”以及“决策树”[15]。本文采用分类正确率较高、学习训练代价较小且重复训练样本也较少的“决策树”分类算法。利用基于决策树的支持向量机建立模型对研究区域进行水质评价，同时与作为参考的单因子评价法和模糊综合评价法的评价结果进行对比分析，以佐证SVM 评价方法的先进性和合理性。

1 研究方法

1.1 原理概述

SVM 分类模型基于结构风险最小化的原理是以分类边界距离最大为目的进行分类识别。样本分类数据分为线性可分和线性不可分2 种情况，当分类数据属于线性可分时，SVM 分类模型通过寻求能够正确划分训练数据集并且几何间隔最大的最优超平面进行模式识别；而当分类数据线性不可分时，则需要将低维空间中线性不可分的样本数据通过非线性映射算法（核函数）转化为在高维特征空间中线性可分的样本分类问题，继而采用线性分类的方法对其进行求解。

假设从某一未知概率分布函数F（x,y）中随机抽取给定训练样本集，｛(xi,yi),i=1,2, …,l｝,xiCRd,yiCR。为使分类超平面可以正确分类所有样本，并使分类间隔最大，其约束条件为：

式中：xi为输入值；w 为可调的权重函数；b 为阈值；w·xi表示向量w 与xi的内积。

（1）当样本分类数据线性可分时，分类间隔为：

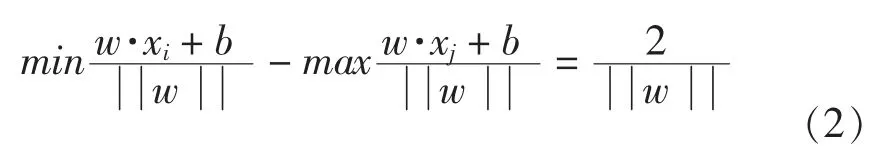
式中：xi为yj=+1 时的值，xj为yj=-1 时的值。

求解最优超平面的问题可转化为约束最优的问题：即在满足约束条件（1）的前提下，通过最小化使得分类间隔最大。这可以通过建立拉格朗日函数的对偶形式来解决：

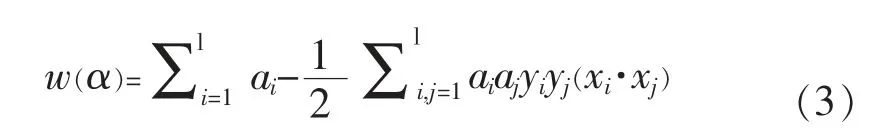
约束条件为：

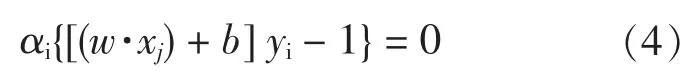
式中：拉格朗日乘子α={α1，…，αN}。

（2）线性不可分数据见图1。由图1 可以看出，三角形和圆形所代表的2 类样本数据是线性不可分时，亦即某些样本数据不满足式（1）条件，则需要引入松弛项ξi来尽可能地降低模型泛化出错的风险。

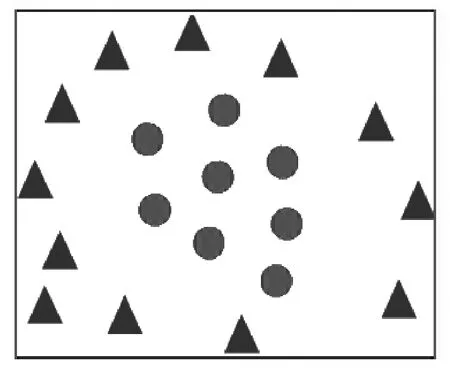
图1 线性不可分数据

约束条件为:

目标函数为：

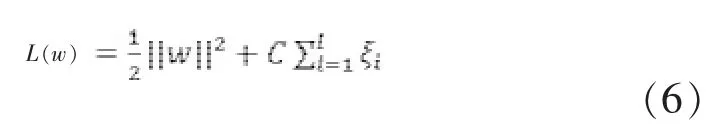
式中：ξ为松弛变量；C 为常数，且C>0，主要用于平衡机器的复杂程度和不可分离点数以及控制错分样本的惩罚程度，C 越大表示对错误的惩罚越重，被称为“惩罚因子”。

SVM 分类模型主要包括“构建分类器、选取训练及验证样本、选择核函数及参数、构建训练模型、模型的验证”5 个步骤。其中关键步骤在于核函数及参数的选择，核函数的选择取决于数据的分布特征，不同的核函数具有不同的特点和适用范围。本文选取的是目前使用最广泛的径向基核函数（RBF），SVM 分类模型中的惩罚系数C 和核函数的参数γ 采用交叉验证的方法来确定这2 个参数的最优组合，并选取交叉的折数V=5 进行C 和γ 的最优求解[17]。

1.2 支持向量机多分类算法

SVM 分类模型最早是针对二分类问题提出的，在实际应用中，有很多问题是多分类问题，例如水质评价问题，因此分类算法的选择对SVM 分类模型深入应用到更多的领域至关重要。徐红敏[16]通过比较SVM 分类模型的3 种多分类算法，得到的结果见表1。其中，“决策树”分类方法在所有SVM 分类模型多类别分类方法中应用较为广泛，它将多类别的各个类别重新组合，同时也考虑结合SVM 分类模型的二类别分类特点，构建的多个子分类器类似于决策树，最终实现多类别分类，解决各种多分类问题。

表1 多类支持向量机分类算法对比

本文采用分类正确率较高、学习训练代价较小且重复训练样本也较少的决策树分类算法。根据不同案例的实际情况构建多个分类器，每个分类器通过相应的样本数据分别进行训练和检验。

2 研究过程

2.1 研究区域

选择某城市一处人工湖泊为研究区域，该人工湖泊地处北亚热带季风区，平均水深约4 m。根据当地对该湖泊制定的水质规划目标，基本达到人类非直接接触娱乐用水以及城市一般工业用水的需求[17]。因此，为使湖泊处于健康良性的发展，同时改善提升整体功能，需对其湖区水质进行长期监测和水质评价。

因SVM 分类模型前期需要一定数量的数据集进行训练和验证，综合考虑实际情况选取该人工湖泊最具代表性的2018年1月～12月的水质数据，分别通过SVM 分类模型、单因子评价法和模糊综合评价法对其水质进行逐月评价分析。该湖泊在线监测点分布见图2。在其湖心设置4 个浮标站并布设8条人工垂线，在7 个支流出入口设置7 个岸边站，在河网关键断面设置10 个集成站。

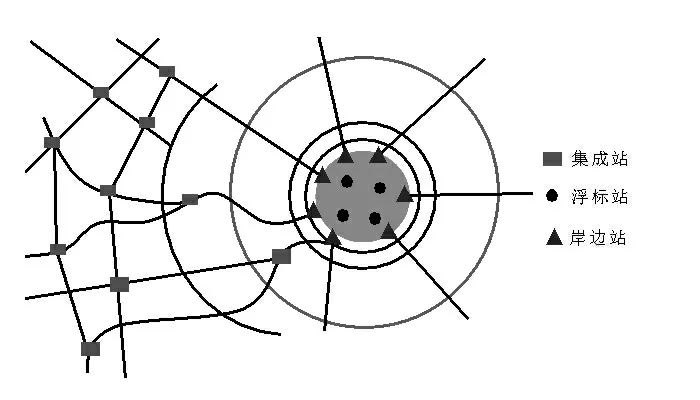
图2 某城市人工湖泊在线监测点分布示意

根据GB 3838—2002《地表水环境质量标准》和该湖泊的限制因子以及其他各种影响因素，从24个地表水环境质量指标中选取DO，CODMn，BOD5，NH3-N，TN，TP 作为主要影响因子进行水质评价，并确认评价等级集合：V={Ⅰ，Ⅱ，Ⅲ，Ⅳ，Ⅴ}。同时，根据岸边站、浮标站以及集成站的水质在线监测数据，结合人工取样监测结果，得到该湖泊2018年12 个月的水质指标数据。

2.2 构建分类器

根据地表水质评价等级，将本文中的地表水质评价案例共分为5 个等级，构建的基于决策树的SVM 分类模型见图3。每个节点是1 个分类器，共构建4 个分类器。

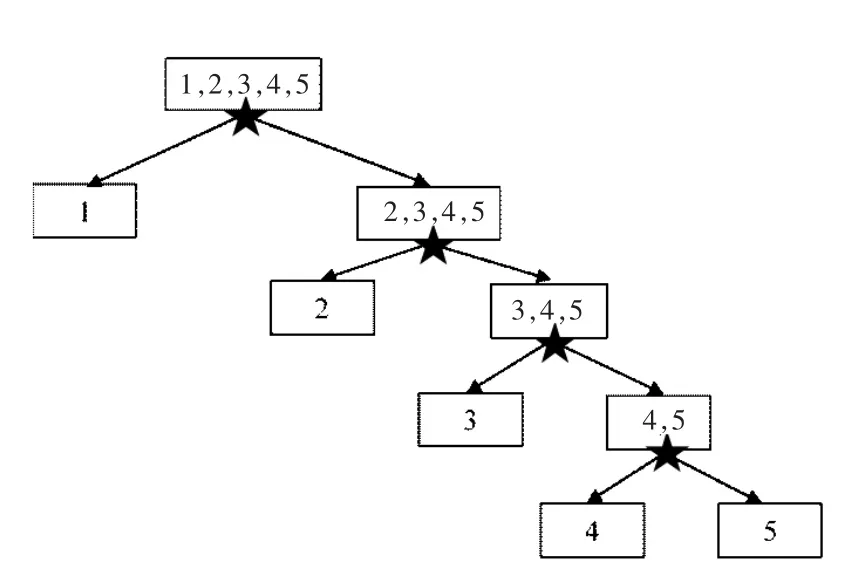
图3 决策树分类模型

2.3 选取训练样本

首先，将2018年该湖泊17 个监测点收集到的412 组监测水质数据，按7 ∶3 的比例划分为288 组训练集和124 组验证集。其次，为消除不同水质指标之间因量级不同所造成的差异，用极差法对国标中选取的6 个指标因子进行归一化无量纲处理，使其数值都归一化至区间[0,1]，具体公式如下：

式中：i=1，2，…，6；j = 1，2，…，5；xmax，xmin分别为国标中各项目因子的最大值和最小值；为归一化处理后的数值。

尽管SVM 分类模型支持小样本训练，但对训练集的数据数量还是有一定的基本要求，以水质评价为例，地表水质分为Ⅰ～Ⅴ类水，5 组阈值组成的训练样本数据难以达到模型训练精度要求，因此为生成足够的训练样本，采取随机插值方法进行插补。选取《地表水环境质量标准》中与样本水质数据对应的污染物指标作为训练样本数据属性，用Matlab R2018a 中的随机均匀分布函数进行加密插值[18]，每个分类器构造出约1 000 组不同区间的标准样本数据。

以分类器一为例，该分类器的目的是将Ⅰ类水和Ⅱ～Ⅴ类水区分开，故加密构造出700 组数据。其中100 组为Ⅰ类水，对应的标签Y1 取值为1；另外600 组为非Ⅰ类水，对应的标签Y1 取值为-1；所有计算均在Windows10 平台上的Matlab R2018a 进行。

2.4 构建训练模型

为实现参数的网格寻优及交叉验证，调用Libsvm 软件包中的grid.py 程序，结合Gnuplot 5.2交互式绘图软件可输出网格法寻优交叉验证的等精度图。首先根据等精度图得到4 个分类器的最优参数组合分别为C = 0.031 25，γ = 2；C = 0.5，γ =0.5；C=2，γ=8；C=0.5，γ=8。然后在Matlab 中编写建模函数语句及调用模型语句，最后构建训练模型进行训练。

2.5 模型的验证与实例评价

模型训练完毕后，为验证模型的泛化能力，还需用验证集进行验证。先将2018年该湖泊12 个月的水质数据进行归一化处理；对于每一个月份，在Matlab 里输入命令：

式中：x1～x6为当月6 个水质指标归一化后的数值；Y 为标签值，可取任意值，此处选取1。

用Matlab 进行逐月水质评价，水质指标变化及水质评价结果详见图5 和表2。

图5 2018年某城市人工湖泊的水质指标变化

表2 SVM 分类模型的水质评价结果

2.6 其他水质评价方法对比

为验证SVM 水质评价模型的优越性，将SVM与其他2 种传统的地表水水质评价方法的差异进行对比分析评价结果见表3。

表3 单因子法、模糊综合评价法和SVM 分类模型的水质评价结果

3 讨论

（1）由图5 可以看出，2018年该人工湖泊水质整体呈变好趋势。根据湖泊水质数据分析，除TP外，CODMn，BOD5，NH3-N，TN 等指标浓度整体下降，DO 指标浓度呈整体上升趋势，TP 指标一直在Ⅲ类和Ⅳ类之间波动变化，而TN 指标则是由Ⅴ类慢慢向Ⅲ类过渡。总体而言，TP 和TN 是主要的减排目标。而单因子评价法和模糊综合评价法的评价结果未能显著表明该人工湖泊水质的细微波动变化。

（2）由表3 可知，单因子评价法的结果均为Ⅳ，Ⅴ类水，该方法是将单一的且最严重的污染物超标程度作为整体水质的表征，虽然评价过程简单直观，但将整体水质均归于Ⅳ，Ⅴ类水显得略为悲观，无益于真实反映水体功效是否满足基本要求，也无法精确描述水环境的实际综合状态。

（3）对比分析SVM 分类模型与模糊综合评价法的评价结果，由图5 和表3 可知，除2月、4月、6月、7月外，其余月份用模糊综合评价法比SVM 均高出1～2 个等级，即评价结果略显悲观；且8月至12月的水质评价结果均为Ⅳ类水质，对前期在现场收集的在线监测数据进行分析得知，除去之前所选取的国标规定的化学指标，其他一些物理和生物指标从侧面也说明了该湖泊水质在11月份有所改善。由此看出，传统模糊综合评价法无法辨别两者更细微的差异，评价结果不能真切描述实际水质情况。相比SVM 分类模型的评价结果更为合理，更贴近实际情况，同时能够辨别水质变化中更加细微的差异。

此外，模糊综合评价法易出现模型“失效”的情况，需要人为给定赋值权重，导致评价结果具有较强的主观性；虽然基于较为精确的数学模型进行描述，但模糊综合评价法忽略了各类评价因子和水质等级之间呈现的复杂的非线性关系，没有很好地解决这个关键问题。相对而言，SVM 水质评价模型则没有水质参评项目个数的限定，能够全面、客观地反映水资源中各水质指标的综合污染程度，在小样本的情况下也能得到较好的分类结果，有助于水环境领域中的决策者作出更加科学客观的决策，为防治水污染、合理利用水资源奠定坚实基础。

虽然SVM 所建立的水质评价模型具有良好的预测能力，支持小样本问题，但由于前期需要数据集对模型进行训练和验证，与传统方法相比较仍需依赖大量的样本数据；同时SVM 作为一个黑箱模型，只能看见输入和输出而非评价过程，对于评价结果的可解释性较差，可考虑与传统统计方法相结合。此外，SVM 分类模型在解决多类的分类问题方面还不完善，需进一步深入研究。

4 结论

以某城市一处人工湖泊的实测数据作为样本，结合实际选取合适的影响因子及相关影响因素作为模型输入量及输出量，基于决策树分类算法的支持向量机（SVM）构建地表水水质评价模型，并与传统水质评价方法的评价结果进行对比分析。得出以下结论：

（1）将SVM 分类模型应用于某城市人工湖泊的水质分类，结果表明，该人工湖泊的整体水质正在好转，这与该人工湖泊各评价指标的分析结果相一致。

（2）将SVM 分类模型与单因子法和模糊综合评价法2 种传统的地表水水质评价方法进行比较，SVM 水质评价模型能客观考虑各项指标和影响因素，既避免了单因子评价法结果的过保护问题，同时没有限制水质参评项目的个数，能够更加客观全面地反映水环境的水质现状及其变化趋势，在小样本的情况下也能得到较好的分类结果，有助于让水管理者更加准确真实地进行水质评价，更好地监督和管理水环境。因此，SVM 分类模型可有效应用于地表水水质评价中。

（3）虽然SVM 分类模型已具有良好的预测能力，但还需进一步研究、完善，比如：①SVM 分类模型与传统统计方法相结合在水质管理中的应用；②SVM 分类模型可考虑结合其他分类算法的优势，提高多类问题的分类精度；③在训练SVM 分类模型的过程中，如何寻求更优的算法模型和选取更适于水质监测与评价的SVM 分类模型核函数及参数。