基于接触式轮廓扫描的螺纹参数提取计算

倪高烽,程维明

（201620 上海市 上海工程技术大学 机械与汽车工程学院）

0 引言

螺纹是机械制造业中最为常见的一种连接形式，主要有紧固、联结、密封和传动等功能，在制造业中有着广泛的应用[1]，保证螺纹精度对整个机械装备制造质量至关重要。除了提高螺纹制造水平外，提高检测水平对于确保螺纹的可靠性更为重要。目前已经有大量的螺纹检测方法，传统的螺纹测量方法主要有三针法、量规法等；现代化的综合测量方法则主要对扫描得到的螺纹二维轮廓点云数据进行多参数的综合计算，轮廓扫描方式主要有接触式和非接触式两种[2]。

国内外学者提出了多种基于二维轮廓点云数据的螺纹参数计算方法。Kosarevsky 和Latypov[3]采用广义霍夫变换对点云数据进行直线提取处理，然后对获得的轮廓直线和交点进行排序并找到与螺纹轮廓直线相切的圆，最后用贝恩特公式求得螺纹参数。但霍夫变换算法其时间复杂度和空间复杂度都很高[4]，并且在检测过程中只能确定直线方向，丢失线段的长度信息。张昊和金冠[5]利用机器视觉原理及边缘提取获得的螺纹二维轮廓点云数据，通过SVM 特征点分类的方法进行点集分类操作，在获得角点点集后分别拟合直线求取螺纹各参数；陈盛等人[6]通过稳健高斯回归滤波对数据进行处理后，再利用复合形模拟退火算法获得相邻两段牙侧线之间距离均方差最小的目标函数，进而计算螺纹各项参数。

以上几种基于二维轮廓数据的螺纹参数计算方法均从螺纹整体出发来计算螺纹的各项参数，无法获取螺纹工件特定牙处或指定段的各项数据，忽略了每个牙形的个体性。本文通过有效的数据匹配算法提取每一牙形，再对每一牙形的大径、小径、中径、螺距、牙形角等参数进行计算，最后在获取整体螺纹参数的同时，也能很好地获取每一牙的各项参数，进而更好地分析螺纹工件的精密性。

1 螺纹采样数据分段组合处理

为获取螺纹的某一轴向剖面轮廓位置坐标数据（如图1 阴影区域所示），接触式螺纹测量采用轮廓仪的测针进行扫描采样。测针在电机的驱动下对被测螺纹上下对称轮廓进行连续扫描，采集机械探针在接触螺纹时的坐标点数据并输入计算机，再通过计算处理可以得到被测螺纹的某一轴向剖面轮廓位置坐标数据[7]，接下来就可以对螺纹采样轮廓坐标数据进行分段组合处理，如图2 所示。

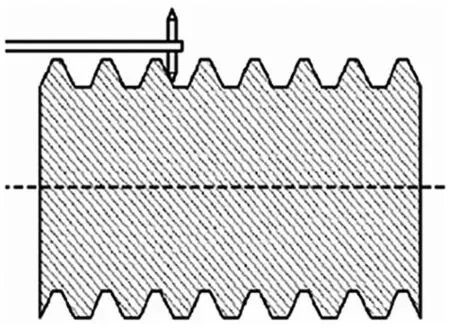
图1 轴向剖面扫描轮廓Fig.1 Axial section scan profile

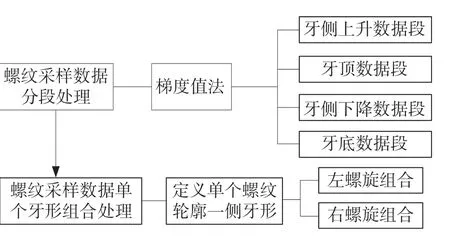
图2 螺纹采样数据分段组合处理流程图Fig.2 Flow chart of segmented combined processing of thread sampling data

1.1 螺纹采样数据分段处理

对于普通公制螺纹来说，在同一牙型周期的相关数据段中的数据点位梯度值处于同一个值区间。例如，如图3 某段螺纹轮廓上表面及图4 该段螺纹点位梯度值图所示，其中右牙侧（牙侧下降段）相邻的采样数据点梯度值都为负值且都小于某一阈值，而左牙侧（上升段）相邻的采样数据点梯度值都为正值且都大于某一阈值，以此可以区分并提取数据中的左右牙侧数据段，具体设定的阈值跟螺纹牙型角α有着直接关系。梯度阈值计算公式为

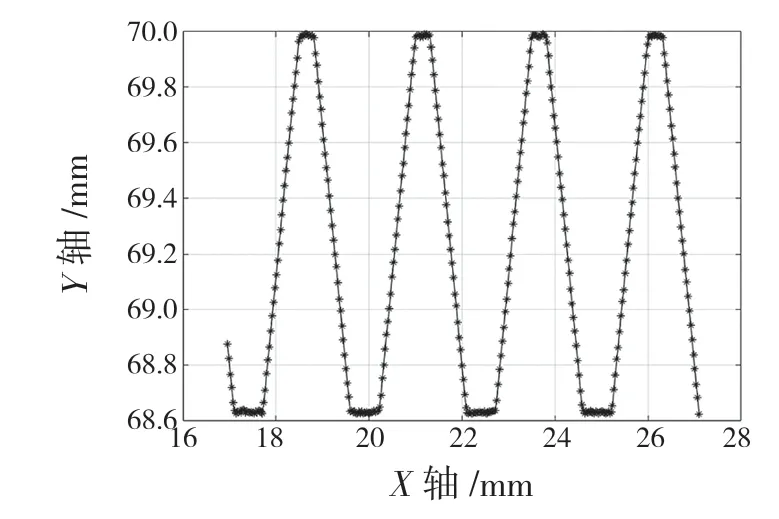
图3 普通螺纹上侧轮廓图Fig.3 Upper side profile of common thread

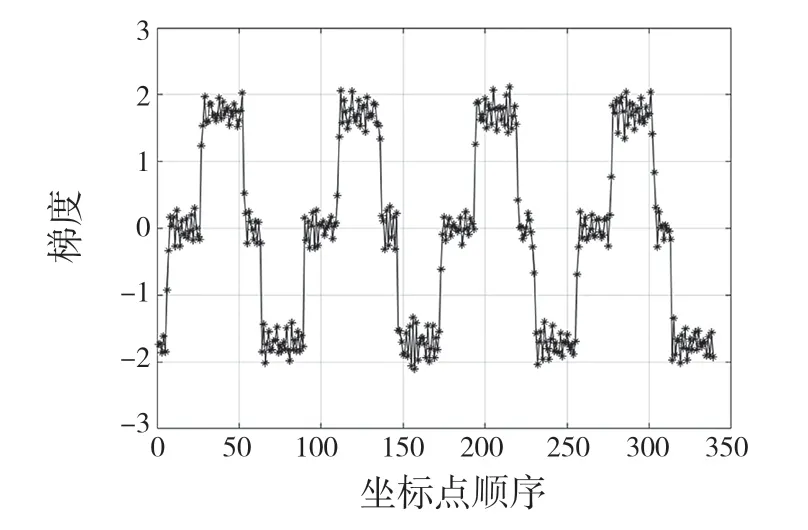
图4 轮廓点云梯度值图Fig.4 Gradient diagram of contour point cloud

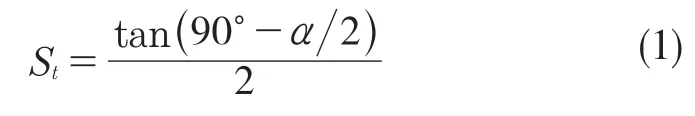
其中tan（90°-α/2），即螺纹牙侧斜率，以除以2 的获得值为分界点区分是牙侧还是牙顶或牙底处的正常表面起伏。正值为区分出左牙侧即牙侧上升段，添加负号为区分出右牙侧即牙侧下降段。

根据普通螺纹60°牙型角可以得到阈值为0.866，梯形螺纹30°牙型角阈值为1.866。而右牙侧数据段（牙侧下降段）接下来就是牙底数据段，左牙侧数据段（牙侧上升段）接下来就是牙顶数据段。

采用梯度值判断法来进行数据分段处理，也能很好地克服测量仪扫描时螺纹轴线倾斜的问题。图 5 所示是螺纹采样数据根据梯度值分类的流程图。

图5 螺纹采样数据分类以及牙形组合程序框图Fig.5 Classification of threaded sampling data and block diagram of tooth shape combination

1.2 螺纹采样数据牙形组合处理

通过梯度值判断法对采集到的数据点进行分段处理后，接下来是将各数据段组合成单个牙形。以上表面螺纹轮廓为例，定义一个螺纹轮廓上侧牙形包含左牙侧+牙顶+右牙侧+牙底，为了方便计算每一牙形的螺距以及中径，再加上下一牙形的左牙侧，因为无法设定扫描获得的数据段开始于牙顶，左右牙侧还是牙底，所以可以分成如图6 所示4 类情况进行分类处理。

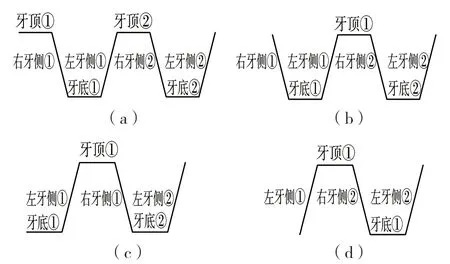
图6 牙形提取情况分类Fig.6 Classification of tooth extraction

情况1:如果从牙顶开始，则第1 个牙形组合为左牙侧1+牙顶2+右牙侧2+牙底2+左牙侧2，则第n 个牙形组合为左牙侧n+牙顶（n+1）+右牙侧（n+1）+牙底（n+1）+左牙侧（n+1）。

情况2:如果从右牙侧开始，则第1 个牙形组合为左牙侧1+牙顶1+右牙侧2+牙底2+左牙侧2，则第n 个牙形组合为左牙侧n+牙顶n+右牙侧（n+1）+牙底（n+1）+左牙侧（n+1）。

情况3:如果从牙底开始，则第1 个牙形组合为左牙侧1+牙顶1+右牙侧1+牙底2+左牙侧2，则第n 个牙形组合为左牙侧n+牙顶n+右牙侧n+牙底（n+1）+左牙侧（n+1）。

情况4:如果从左牙侧开始，则第1 个牙形组合为左牙侧1+牙顶1+右牙侧1+牙底1+左牙侧2，则第n 个牙形组合为左牙侧n+牙顶n+右牙侧n+牙底n+左牙侧（n+1）。

情况4 特例说明：当第1 组左牙侧点数过少时，会影响后续中径线的提取以及牙型角的计算，故当点数少于2 个时，将该组牙型标记出来，不做计算，只占一个牙形组的标号位置。

螺纹轮廓下表面牙形分类组合的方式与上表面方法一样。当上下表面两侧牙形组合完成后，最后就是将对应的上下表面轮廓的单个牙形进行匹配组合。上下螺纹轮廓同一相匹配的单个牙形在轴向相差大约半个螺距的距离，基于此条规则，可以将上下螺纹轮廓的单个牙形相配对成整个完整的牙形。由于螺纹存在左右旋之分，所以匹配时也需要注意区分。如图7 所示，理论上，右旋的螺纹下侧轮廓的牙形点云数据x 坐标（轴向坐标）比上侧轮廓的牙形点云数据x 坐标（轴向坐标）大半个螺距；左旋螺纹相反，下侧轮廓的牙形点云数据x 坐标（轴向坐标）比上侧轮廓的牙形点云数据x 坐标（轴向坐标）小半个螺距。螺距P 可以在获得每一侧牙形组合后利用定义事先求出。

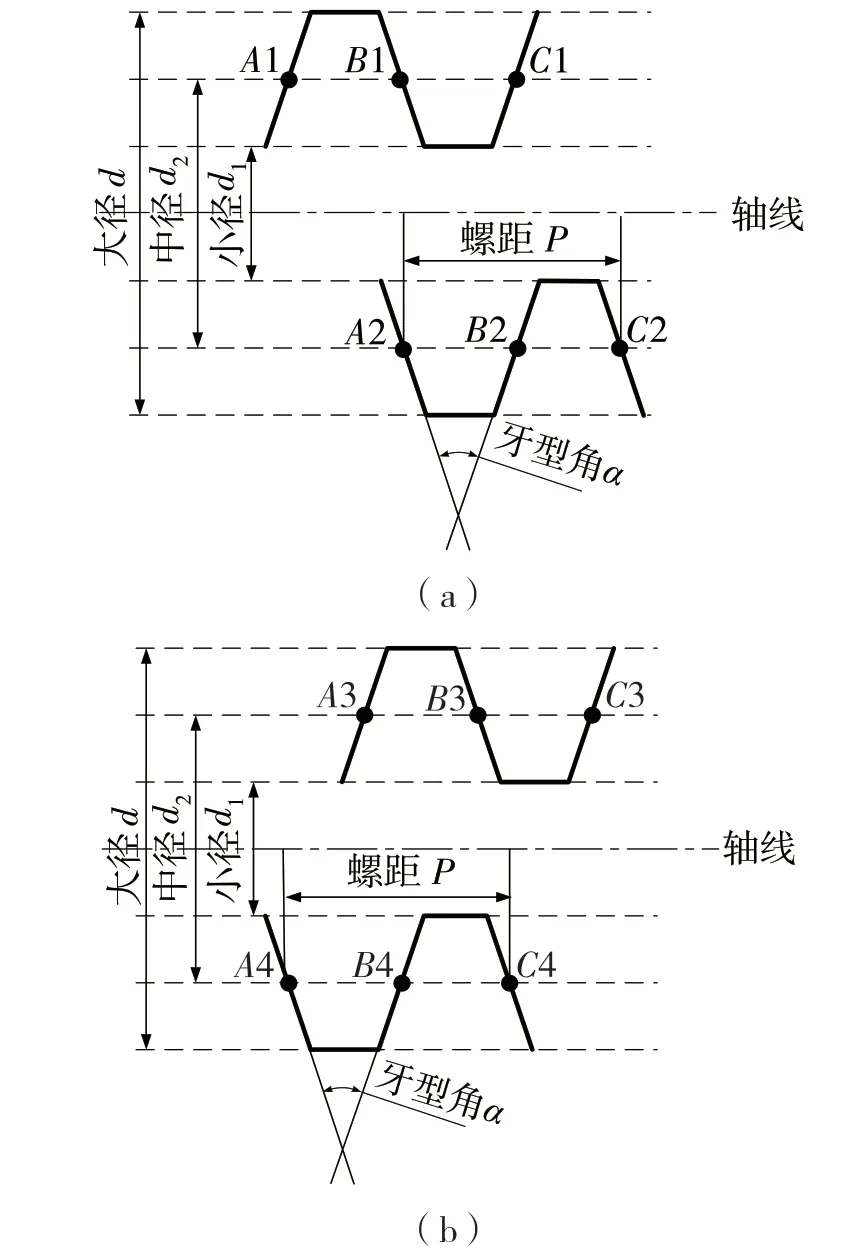
图7 单个牙形旋向组合Fig.7 Single tooth rotation combination

实际求取过程中存在误差，这里以中径线所在直线与牙侧交点坐标作为配对标准点。图7（a）上表面中径线与牙侧交于点B1（x1，z1），下表面中径线与牙侧交于点B2（x2，z2），当满足式（2 ）时配对为一组牙型组合。

式中：P/2——半个螺距；δ（δ

同样，图7（b）上表面中径线与牙侧交于点B3（x3，z3），下表面中径线与牙侧交于点B4（x4，z4），当满足式（3 ）时配对为一组牙型组合。

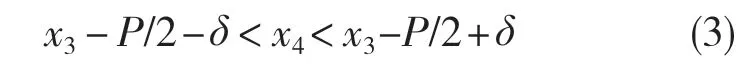
式中：P/2——半个螺距；δ（δ

2 螺纹参数计算

螺纹指的是在圆柱或圆锥母体表面上制出的螺旋线形的、具有特定截面的连续凸起部分[8]。普通螺纹的基本牙型能很好地反映螺纹的基本尺寸，梯形螺纹和管螺纹等其他型号螺纹的基本牙型可看作是在普通螺纹基本牙型基础上的调整，与普通螺纹基本牙型相似或相同。需要提取的主要参数有：大径d、小径d1、中径d2、螺距P、牙型角α等。这里以组合后的单个右螺旋牙形为例，在螺纹轮廓点云数据分段的基础上利用最小二乘拟合直线，进而可以求得每段直线方程参数的（k，b）：

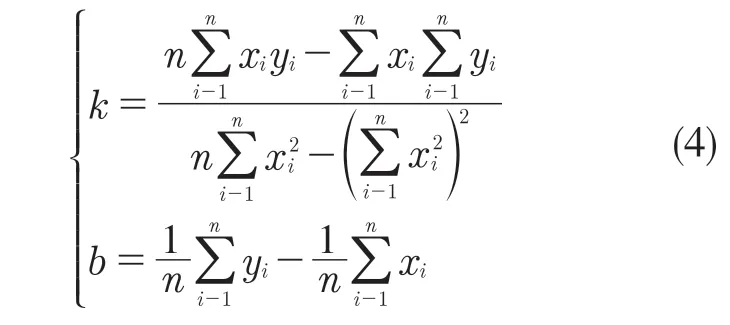
2.1 螺纹轴线的确定

在牙形分段处理后，获得全部的牙顶数据段，通过最小二乘法分别拟合得到的上下表面轮廓线lup：z=kupx+bup和llower：z=klowerx+blower。实测获得的螺纹数据上下表面的轮廓拟合直线并不平行，存在一定夹角，所以螺纹工件的螺纹轴线在测量平面内的投影直线为lup和llower的角平分线。如图8 所示，图中模拟的螺纹上下表面轮廓倾斜度经过放大处理，实际上下表面轮廓线lup和llower拟合直线夹角很小。设螺纹工件的螺纹轴线laxis：z=kaxisx+baxis根据式（5 ）可以得到2 个kaxis，取绝对值最小的为轴线斜率，另一个为补角的角平分线。再将lup和llower的交点代入螺纹轴线方程求出截距，从而求出螺纹轴线方程。

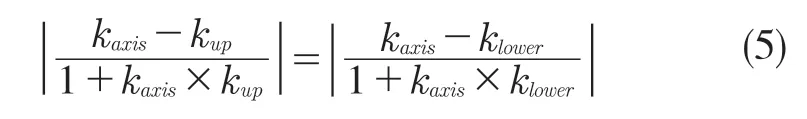
图8 螺纹轴线计算示意图Fig.8 Calculation diagram of thread axis

2.2 螺纹大小径的计算

螺纹大径指的是与外螺纹牙顶相切的假想圆柱体或圆锥体的直径，螺纹小径指的是与外螺纹牙底相切的假想圆柱体或圆锥体的直径。通过上下螺纹轮廓牙顶的数据来计算螺纹大径，计算拟合此位置的直线，然后求出上下表面牙顶拟合直线的距离就是螺纹大径，用这种方法也可以求出螺纹小径[9]。如图9 所示，通过前面方法进行直线拟合La的方程，z=k1x+b1，Lb的方程，z=k2x+b2。理论上La和 Lb是两条平行的直线，但由于螺纹的制造误差、测针扫描以及后续数据处理时的误差，使得 La与Lb两直线可能不平行，所以通过计算点到直线距离来计算出螺纹的大径值。在 La上选n 点，求点到直线Lb的距离平均值；同理，在Lb上取m 点，求到直线Lb的距离平均值。最后根据式（6）可得到大径值。

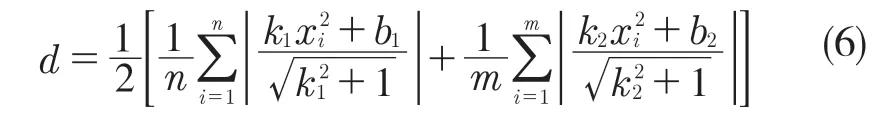
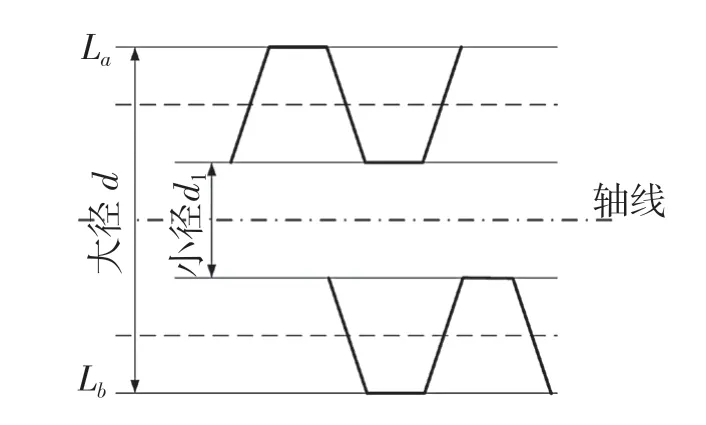
图9 螺纹大小径拟合Fig.9 Fitting of thread big and small diameters

2.3 螺纹中径的计算

螺纹中径是指一个假想圆柱或圆锥，该圆柱或圆锥的母线通过螺纹牙型上沟槽和凸起宽度相等的地方的直径[10]。根据中径的定义，在牙型截面内沟槽和凸起宽度相等的地方就是中径所在的圆柱母线。对于本文提取的单个牙型轮廓曲线，可以根据3 个左右牙侧，构造直线方程L1，L2和L3，如图10 所示。然后作出任意一条直线Ld'与前文求得的螺纹轴线平行且与螺纹左右牙侧拟合的直线相交于点 A（x1，z1），B（x2，z2），C（x3，z3），若满足式（7），则Ld'为螺纹中径处螺纹母线。如果不满足该条件，可以作线段AB 的中垂线N1N2与螺纹右牙侧拟合直线L2交与E 点，过E 点做平行于螺纹轴线的直线Ld与螺纹左右牙侧拟合直线L1，L2交于点 D 和点F，此时有 DE=DF，所作的直线Ld即为所求得中径所在直线。求出中径所在直线后，两中径所在直线的距离即为中径，方法与大小径一样。

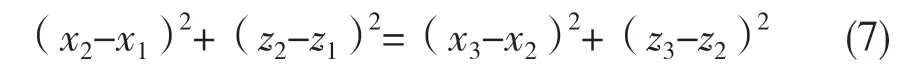
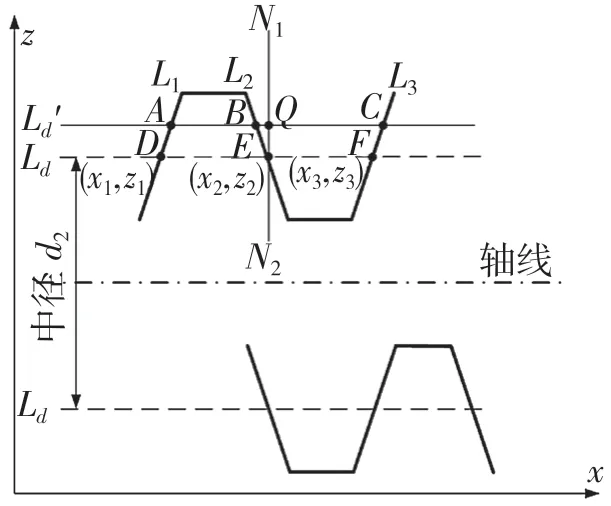
图10 螺纹中径线拟合Fig.10 Middle diameter line fitting of thread

2.4 螺纹螺距的计算

螺距是指相邻两牙在中径线上对应两点间的轴向距离。由螺距定义可知，螺距是在测量中径所在的母线上相邻两牙之间的轴向距离，因此螺距P 是在螺纹中径拟合出的母线上进行计算的。如图10 所示，由中径拟合直线过程可知，中径线Ld与螺纹的牙侧线相交于若干点，每个螺纹牙同侧的交点如D，F 之间的距离就是螺距，那么计算出多个同侧交点间的距离后求均值，就可以得到螺距的测量值。则螺距 P 计算公式为

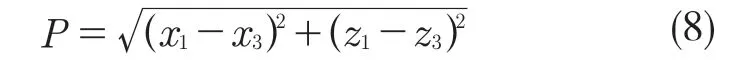
2.5 螺纹牙型角的计算

螺纹牙型角指的是螺纹牙型上相邻两牙侧间的夹角，而牙型半角指的是螺纹牙侧直线与螺纹轴线的垂直线线间的夹角。如图11 所示，同一螺纹牙型的左右两个牙型半角之和即为该螺纹牙型的牙型角。

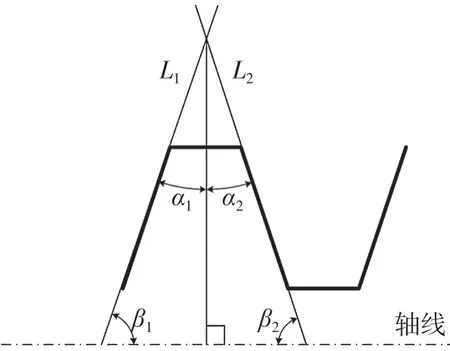
图11 螺纹牙型角拟合Fig.11 Fitting of thread shape angle

根据牙型角两边牙侧之前拟合的直线L1，L2，求得的两直线斜率分别为k1和k2，前文求得的螺纹轴线斜率kaxis，则L1和L2与螺纹轴线的夹角公式分别为

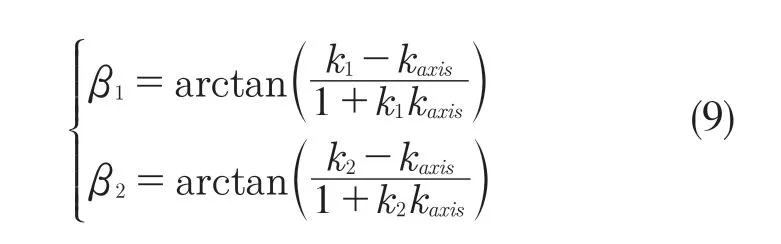
进而得到左右牙型半角的公式为

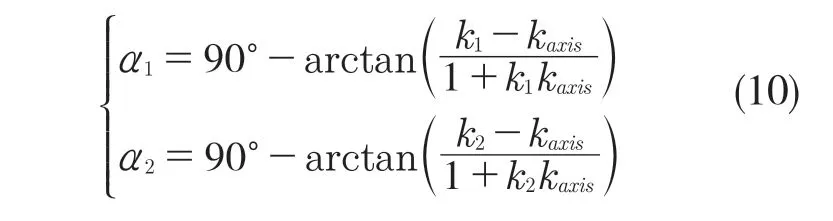
则牙型角α为

也可以根据牙型角的定义可知，根据式（12）直接求得牙型角大小

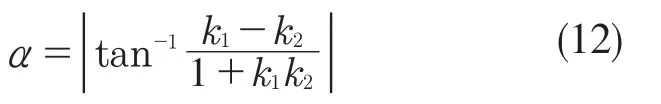
2.6 测试结果及分析

对参数计算算法进行测试和分析。本文采用实测的M25X2.5 的普通螺纹点云数据，借助MATLAB 进行算法程序设计并对测量数据进行分析处理，最后设计图形用户界面进行效果展示，如图12 所示。

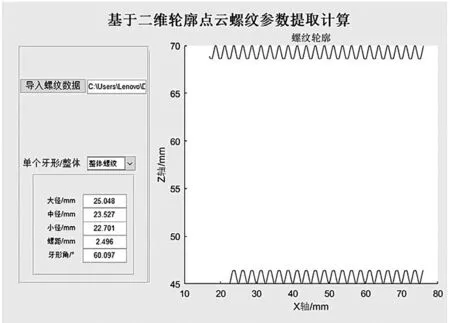
图12 图形用户界面Fig.12 Graphical user interface

测试结果得到螺纹主要参数如表1 所示。可以看出测得的螺纹大径为25.048 mm，螺距为2.496 mm；螺纹的牙型角值为60.098°，测试结果也可以分析单个牙形的各参数并判断其是否合格。通过该方法计算获得的螺纹参数，在保证精度的同时，也使获得的结果更加多样化。

表1 螺纹测量结果Tab.1 Thread measurement results

3 结语

本文采用梯度值判断法对获得的螺纹二维轮廓点云数据进行分类，然后根据所提出的螺纹单个牙形的匹配规则进行牙形提取，再利用螺纹的各参数计算方法得出每一牙的螺纹参数数值，同时也得到螺纹整体参数。最后利用实测螺纹点云数据，通过MATLAB 程序设计进行提取计算，结果表明，该方法在保证螺纹检测精度的同时，也可以获取被测螺纹工件特定牙处或指定段的各项数据，扩展了测量结果的多样性，解决了目前基于螺纹二维轮廓点云的多参数测量方法大多无法获取螺纹单个牙形参数的问题。