两类具有激波层性态的奇摄动边值问题

马晴晴，张志明

(阜阳师范大学 数学与统计学院，安徽 阜阳 236037)

摄动方法随着内层问题的深入研究而不断发展，内层与边界层不同之处在于，有许多实际问题其中急剧的变化发生在感兴趣区域的内部。例如从流体力学、固体力学和气体动力学等物理问题中建立的模型压缩流以及从混合燃烧、催化反应和稳态浓度等化学问题中导出的化学反应流，往往会出现激波层等性态，这里考虑两种具有激波层性态的边值问题，对论文[1]的结果进行了推广。

考虑一般的二阶奇摄动Dirichlit 问题

其中：ε是任意小的正数,A、B是任意给定的常数。

假设uL(t)和uR(t)分别为退化问题

在[a,b]的解，把解uL(t)和uR(t)分别称为退化问题的左解和右解。若问题(1)和(2)的解在t0∈(a,b)具有内层性质或者说呈內层性态，则根据左、右解及其左、右导数在t0的取值情形分类如下

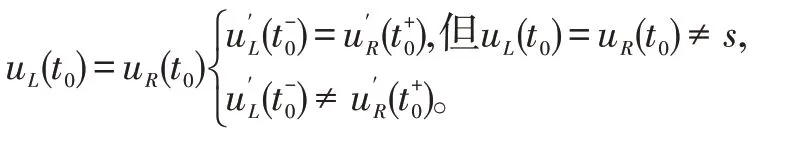
衔接法主要用于uL(t0)≠uR(t0)的情形。相应的内层分别称为激波层和非单调过渡层，本文主要考虑第一种性态即激波层性态，给出如下定义。

定义1[1]若问题(1)，(2)在[a,b]上的一个解x=x(t,ε)满足

其中：uL(t0)≠uR(t0)，且s介于uL(t0)与uR(t0)之间，则称解x(t,ε)在t=t0处呈激波层性态。

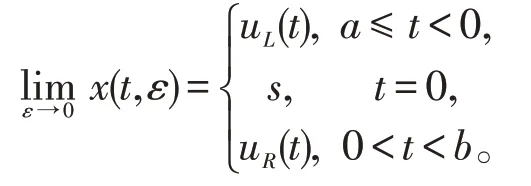
uL(0)≠uR(0)，且s介于uL(0)与uR(0)之间。

2 一类拟线性边值问题

Cole[1]较早研究如下拟线性的边值问题

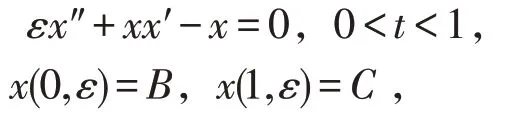
其中：B,C是已知常数。当边界值B和C产生变化时，此边值问题除了在端点t=0(或t=1)处出现边界层之外，当其满足以下条件：

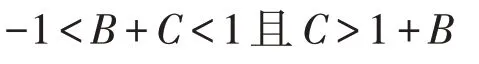
时，激波层性态在内点t0=(1-B-C)∈(0,1)处就会出现。当然，这个有趣的问题引起大部分学者的[2-6]的兴趣，莫嘉琪等[7-12]做了如下罗宾问题

详细讨论了可能的激波位置，给出了激波解[13-18]的渐近表达式。

考虑一类更加一般的拟线性边值问题

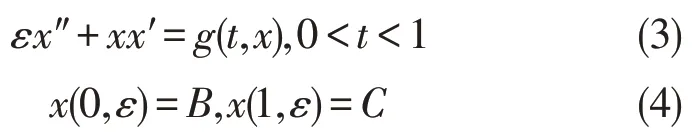
其中：g(t,x) 在[0,1] ×R上连续，且存在函数uL(t),uR(t)∈C2[0,1],分别满足退化问题

使得uL(t)+uR(t) 为[0,1] 上的单调函数，uL(t)≠uR(t)。

由于uL(t)≠uR(t)，由于问题的解(如果存在)存在边界层或内层现象，这里分析了该问题的解在t0∈(0,1)处如果呈现激波层状态，那么它的条件是什么,最后通过匹配渐近展开法[19-20]在表面构造出在[0,1]上具有一直有效性的激波层渐近解。

将外展开式x0=代入(3)和x(0,ε)=-B或x(1,ε)=C,令ε0的系数相等即可得

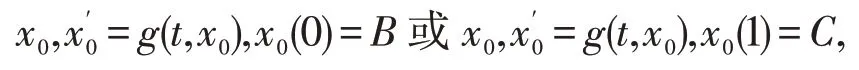
可知它们对应的是退化问题(5)和退化问题(6)，由假设可知，其解x0=uL(t)和x0=uR(t)表示为

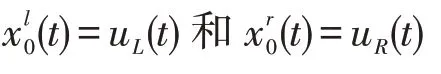
现假设激波层在内点t0∈(0,1)出现，那么对t0处引入伸展变换

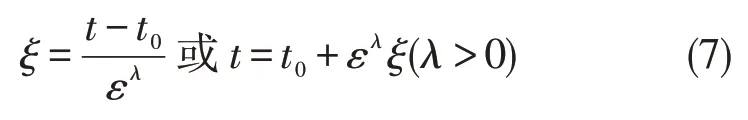
将(7)代入(3)得到

由此可知特异极限会在λ=1 时出现,该方程写为

设内展开式形式为

将它代入(8)，并令ε0的系数相等可得

从(9)解出

另外，我们也可以通过刘姥姥与贾雨村形成对比，我们知道他们都相当于打秋风的人，但是两个人对恩人的表现却十分不同，贾雨村尽管有时会在利益的诱惑下帮助恩人，但大多是助纣为虐，而最终在没有利益的时候，在要付出巨大的代价的时候，贾雨村选择了背叛恩人，还落井下石，让我们看到了人性丑恶的一面，而刘姥姥却不一样，她用自己的一切选择了帮助恩人，尽管恩人当时已经不能再给她任何好处了，而且刘姥姥还要付出巨大的代价，所以人性的善恶通过这两个人我们就可以清晰地看到，此外，这两个人的安排也十分巧妙，都是从头到尾的线索人物，让我们看到了曹雪芹写作技巧的高超。

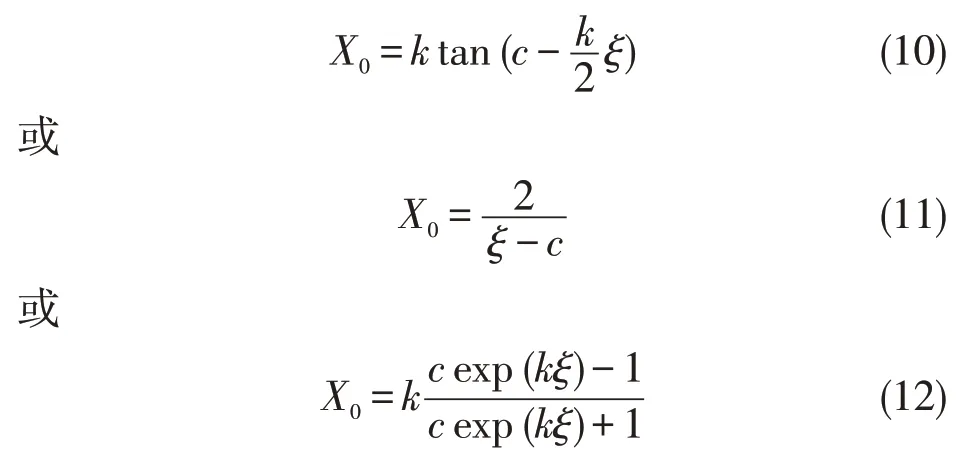
k,c为积分常数并且k≠0，不失一般性，取k＞0，根据匹配原则，应有

由此定出

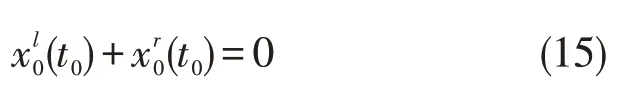
可发现假设在t=t0(即ξ=0)处有激波层，得出X0(0)=0。因此从(12)给出c=1，有

综合上面的讨论，得到复合展开式

其中k和t0的值由(14)，(15)确定。

3 一类两次边值问题

考虑如下形式的二次问题

其 中0 ＜ε＜＜1,a,b(a＜0 ＜b) 。讨论 了 当t=0 是f(t)的高阶转向点的问题(17),(18)并分析了它们在t=0 处存在激波解的条件，利用合成展开法把这个问题的形式渐近解构造出来，再应用微分不等式理论来证明当ε→0 时解的渐近性质和激波解的存在性，假设

H1：存在函数uL(t),uR(t)∈C2[a,b]分别满足退化问题

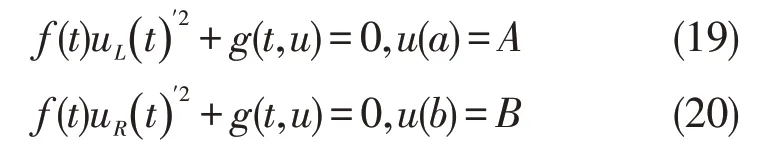
H2：f(t)∈Cn[a,b](n≥3) 使f(0)=f′(0)=…=f(n-1)(0)=0 且f(n)(0)≠0，即t=0 为f(t)的n阶转向点。

H3：g(t,x)∈C1([ ]a,b×R)，且存在常数l＞0，使gx(0,x)≥l。

使用合成展开法来简单地构造问题(17)和(18)的零次形式近似，这里先将外部解

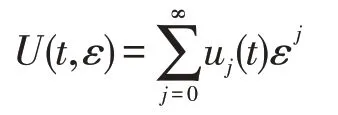
代入(17)和u(a,ε)=A或(u(b,ε)=B)。因此可知道外部解的零次近似u0=uL(t)和uo=uR(t)，它们分别是退化问题(19)和(20)在[a,b]上的解。

因为uL(0)≠uR(0)，需要在t=0 附近构造激波层校正项

其中ε=为伸展变量，将U(t,ε)+V(ξ,ε)代人(3)得到

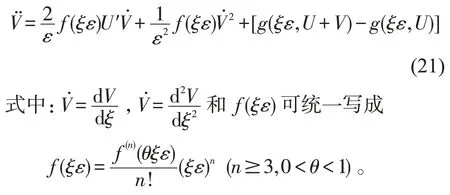
其中：g(ξε,U)和g(ξε,U+V)分别表示为

其中：0 ＜θi＜1(i=1,2)；η介于u0(0)与U之间；ξ介于u0(0)+v0与U+V之间；u0(0)=uL(0)或uR(0)。在(21)中令ε0的系数相等可得

当取u0(0)=uL(0)时，相应的v0(ξ)记作vL(ξ)，考虑到vL(ξ)作为激波层在(]-∞,0 上的主要校正项，应满足vL(-∞)=0，v˙L(-∞)=0，故从(22)推出

类似地，当取u0(0)=uR(0)时，vR(ξ)(ξ∈[0,+∞))应满足vR(+∞)=0,v˙R(+∞)=0,

从而有

其中

下面讨论uR(0)＞uL(0)的情况(类似地可以讨论uR(0)＜uL(0)的情况)，仍可由激波层校正项的性质得到v˙0(ξ)＞0(v0=vL或vR)，故从(23)和(24)推出

且vL(ξ)和vR(ξ)可分别表示为

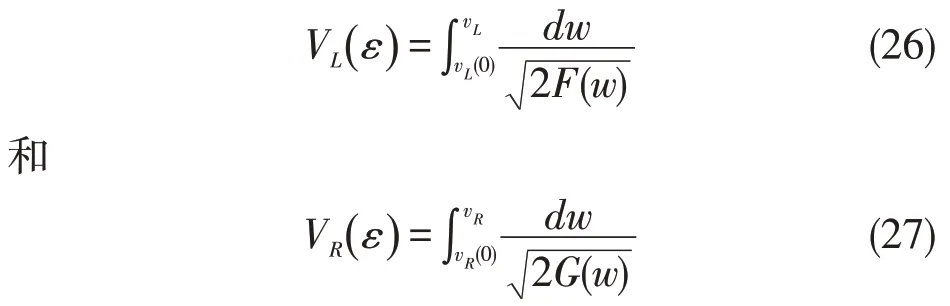
用衔接法，若令

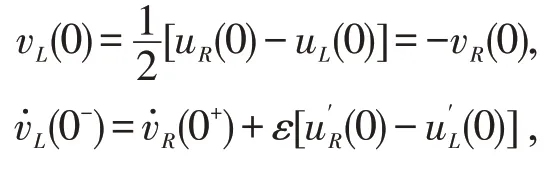
就有

而(25)可改写为

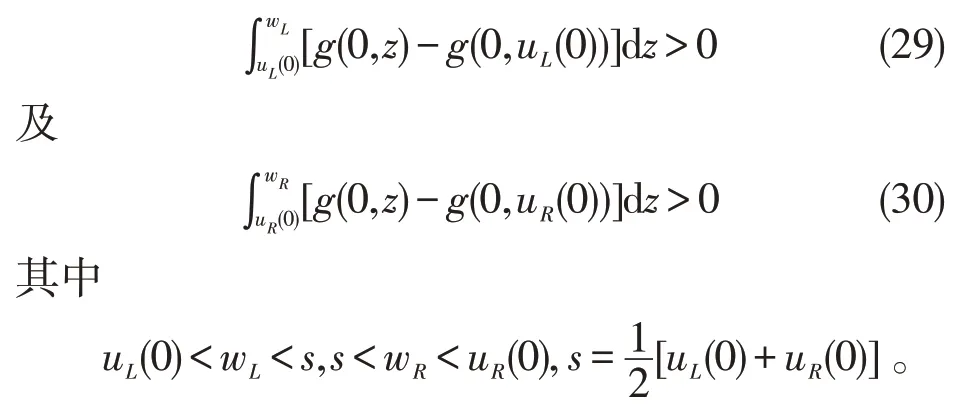
于是得到问题(17)，(18)的解

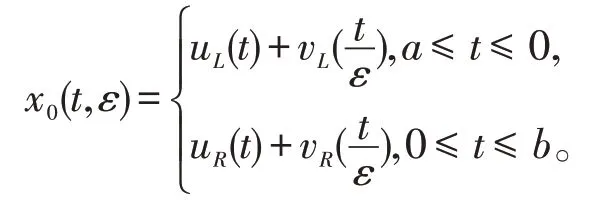
再利用微分不等式的理论，从而去证明当ε→0 时解的渐近性质及激波解的存在性。

定理1在H1～H3下，并假设

H4：uR(0)＞uL(0)，且条件(29)和不等式(29)，(30)成立，那么存在充分小的正数ε0，使对于每个0 ＜ε≤ε0，在问题(17)，(18 的区间[a,b]中，在t=0时有激波层性态的一个解x(t,ε)，并且在[a,b]上一致有x(t,ε)=x0(t,ε)+O(ε)。

证明先说明由(26)所确定的vL(ξ)当ξ→-∞时为指数型小项(记为EST），事实上，由假设H3知对任意z∈(0,vL(0))，g(0,uL(0)+z)-g(0,uL(0))≥lz,

随之有

因此vL≤vL(0)exp(kξ)。

所以

当ξ＞0 时，vR(ξ)∈(vR(0),0)，类似讨论得到

其中τ介于u0(0)+v0与u0+v0-rε之间，于是可取r≥，这里K＞0 使|O(ε) |≤Kε，

由假设H3推出

类似可得

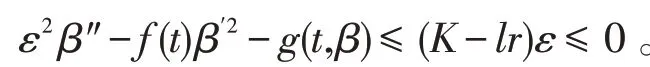
又显然在[a,b] 上a(t,ε)≤β(t,ε)，且由(31)，(32)可知，只要保证ε充分小，就可得α(a,ε)≤A≤β(a,ε)和α(b,ε)≤B≤β(b,ε)。

应用微分不等式理论，推出问题(17)、(18)在区间[a,b] 上存在一个解x(t,ε)，并且满足

故当ε→0 时在区间[a,b] 上一致地有

且uL(0)≠uR(0),s=[uL(0)+uR(0)] 是在uL与uR(0)之间的，所以解x(t,ε)在t=0 处呈现激波层性态。定理证毕。

3 小结

在研究奇摄动的内层问题时，提出了一种构造方法，称为衔接法:即通过分别构造内层两边解的近似，然后平滑地连接相应的曲线，形成整个区间上解的近似表达式。本文用它研究了两种奇摄动边值问题中的激波层性态，进一步可考虑非单调过渡层的奇摄动边值问题。