时滞神经网络的间歇型非脆弱状态估计

崔 颖，张鑫烨

(阜阳师范大学 数学与统计学院，安徽 阜阳 236037)

近年来，联想记忆[1]、模型识别[2]、裂缝检测[3]等在神经网络方面得到了广泛的应用[4-5]。在神经网络的运行过程中，放大器的切换速度或信号传播时间的有限性往往导致神经网络的时滞现象。例如，CUI 应用平均驻留时间方法研究了一类离散型的混合时滞神经网络的稳定性[6]。黄寿星等针对一类具有比例时滞的神经网络模型，利用Gronwall 积分不等式建立了全局指数稳定性判据[7]。

另一方面，由于神经网络的内部状态信息难以直接测量，这就需要设计状态估计器，利用可测量的数据估计神经网络内部的状态信息[8]。在过去的几十年里，状态估计理论得到了很好的发展，并在许多现实应用中得到了广泛的应用，如目标跟踪[9]、环境监测[10]、电力系统[11]等。截至目前，已经提出了各种状态估计技术，包括H∞状态估计[12]、l2-l∞状态估计[13-14]、Kalman-型状态估计[15-16]。在实际工程中，状态估计器在运行时，其参数往往会受到某种程度的波动影响。因此，有必要设计具有非脆弱性的状态估计器，即当参数在某种范围内变化时，估计器的性能不会改变。现在，关于非脆弱估计器的设计已有了一些研究结果。SHEN Y J 针对一类离散型的多速率时滞系统，研究了非脆弱型H∞滤波的设计[17]。刘源等研究了具有随机切换非线性的时滞神经网络的非脆弱状态估计问题，通过应用Lyapunov 稳定性和随机分析方法，给出了满足均方渐近稳定的非脆弱状态估计器存在的条件[18]。

此外，为更好地提高资源利用率，我们期望在估计器间歇工作情形下，CUI Y 研究状态估计器的设计问题。例如，通过切换信号刻画了采样数据的间歇传输现象，进而运用切换系统的稳定性分析方法设计了时滞复杂网络模型的间歇型状态估计器[19]。然而，针对时滞神经网络模型，间歇型的非脆弱状态估计问题还有待进一步研究。

基于上面的分析，本文将针对时滞神经网络模型，研究其间歇型的非脆弱状态估计问器的设计问题。所考虑的估计器允许数据间歇传输，并且其控制参数满足范数有界的不确定性。首先，借助Lyapunov 稳定性和矩阵不等式，给出了间歇型非脆弱估计器的存在条件，指出当估计器的停歇率在一定范围内，误差系统是鲁棒指数稳定的。然后，估计器的增益矩阵通过线性矩阵不等式的可行解表示。

1 模型的刻画

考虑连续型时滞神经网络

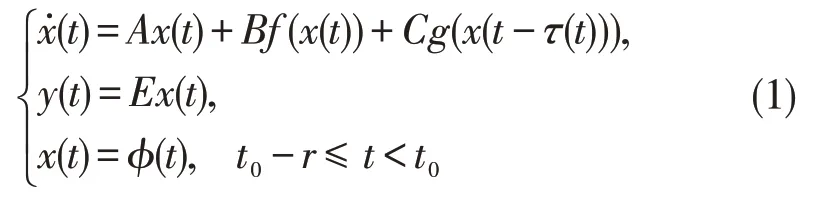
其中x(t)∈ℝ″为神经网络的状态向量，y(t)∈ℝq为输出向量，φ(t)为此神经网络的初始状态。对角矩阵A=diag{a1,a2,…,an}（||ai＜1）表示神经元的自反馈矩阵，矩阵B和C分别为神经元之间的连接加权矩阵和时滞连接加权矩阵，矩阵E为此神经网络的状态输出矩阵，τ(t)表示时变的离散时滞，满足0 ≤τ(t)≤r和0 ≤τ˙(t)≤τ＜1。向量值函数

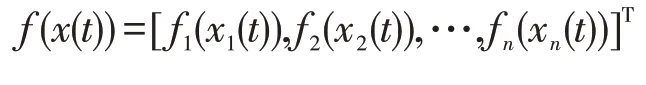
和

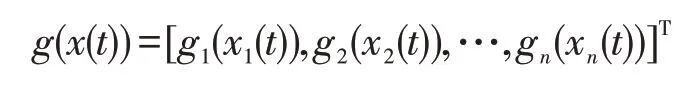
表示神经网络的激励函数，满足下面的扇形有界条件。

假设1[6]神经网络(1)中激励函数f(x),g(x)满足

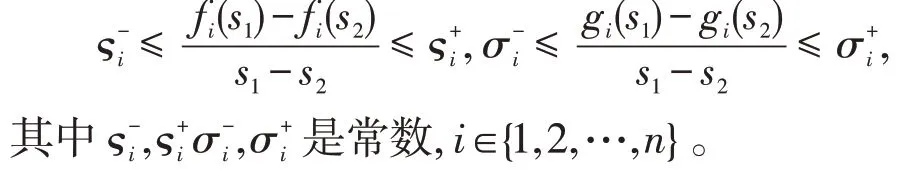
为了获取神经网络(1)的内部状态，设计神经网络(1)的状态估计器。于是，针对神经网络(1)，考虑如下的全阶状态估计器

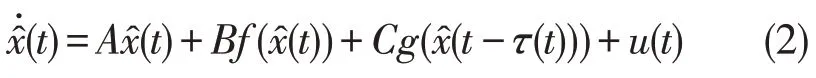
在实际工程中，由于各种复杂多变的环境，状态估计器的参数往往会受到一定程度的扰动，因此，在设计状态估计器时，期望估计器的控制参数能够在允许的范围内变化。此外，为了更好地提高资源的利用率，考虑在间歇工作的情形下，设计具有非脆弱性质的状态估计器。为此，将引入切换信号σ(t)刻画估计器的间歇工作情形。具体地，若估计器正常工作，记σ(t)=1，若估计器停止工作，记σ(t)=2。在[)t0,t上，设σ(t)的切换时间序列为{tj},满足t0＜t1＜t2＜…＜tk＜t。在[t0,t)上，记估计器正常工作的总时间为T-(t,t0)，停止工作的总时间为T+(t,t0)，并称δ=为估计器的停歇率。

于是，借助已引入切换信号σ(t)，间歇型非脆弱的全阶估计器(2)的控制输入为

其中K为待设计的估计器增益矩阵，增益矩阵的变化ΔK(t)满足

这里FT(t)F(t)≤I,∀t≥t0。

定义状态误差向量为e(t)=-x(t)，于是，由系统(1)与(2)，估计误差系统为

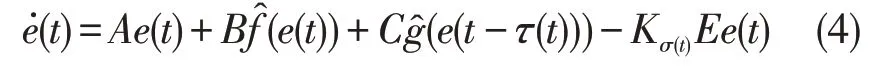
其中

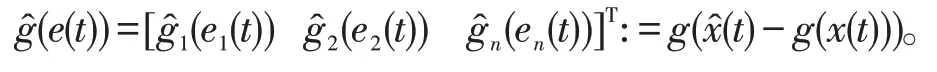
定义1若存在常数C＞0，λ＞0，使得增益矩阵的改变量ΔK(t)在满足条件(3)之下，误差系统(4)的任一解e(t)均满足‖e(t)‖ ≤，∀t≥t0,则称估计误差系统(4)是鲁棒指数稳定的。

本文中将针对连续型时滞神经网络(1)，设计间歇型的非脆弱状态估计器(2)，使估计误差系统(4)是鲁棒指数稳定的。

2 主要结果和证明

首先，运用Lyapunov 稳定性方法和一些矩阵不等性给出间歇型非脆弱状态估计器(2)的存在条件。接着，通过线性矩阵不等式的可行解表示出所设计状态估计器的增益矩阵。为此，先给出如下的引理。

引理1[20]设实矩阵M,N和F具有恰当维数，且FTF≤I，那么对任意的正数ε，有

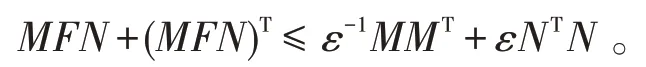
接下来，给出间歇型非脆弱状态器(2)存在的充分条件。

定理1对于给定的估计增益矩阵K和正数λ，若存在正定矩阵P，Q，对角矩阵Γ，Ξ 和正常数ε，使得下面的矩阵不等式成立

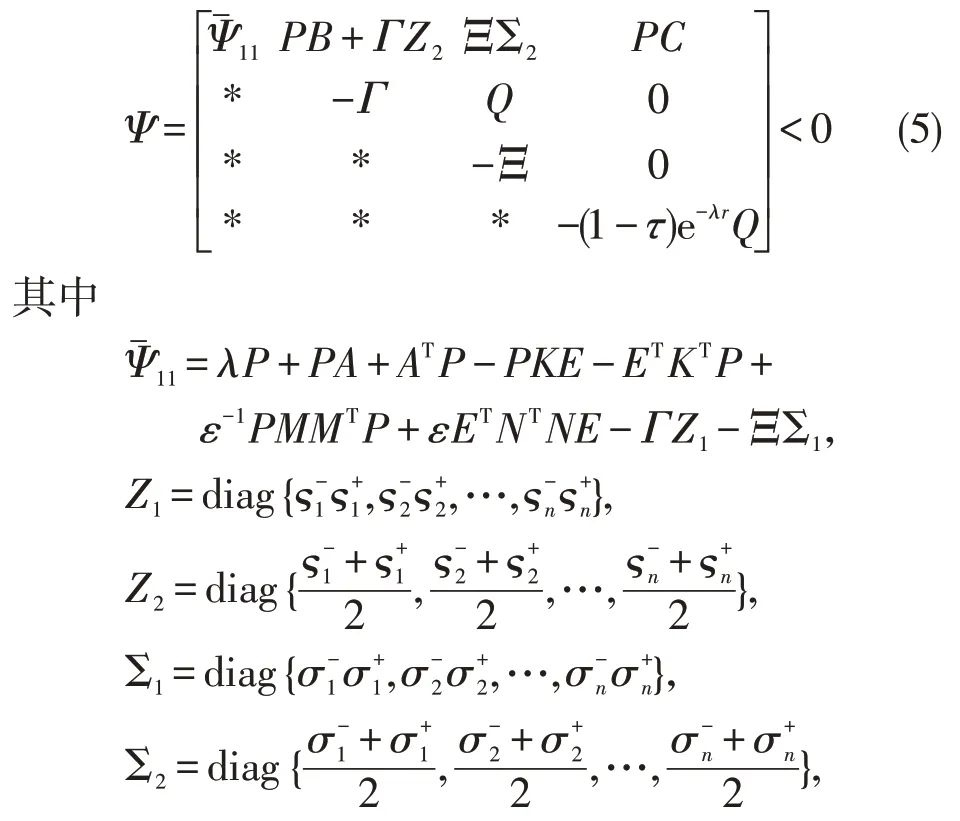
则当停歇率δ＜(α=(1+‖K‖ +‖M‖ ·‖N‖)‖E‖)时，估计误差系统(4)是鲁棒指数稳定。

证明考虑如下的Lyapunov 泛函

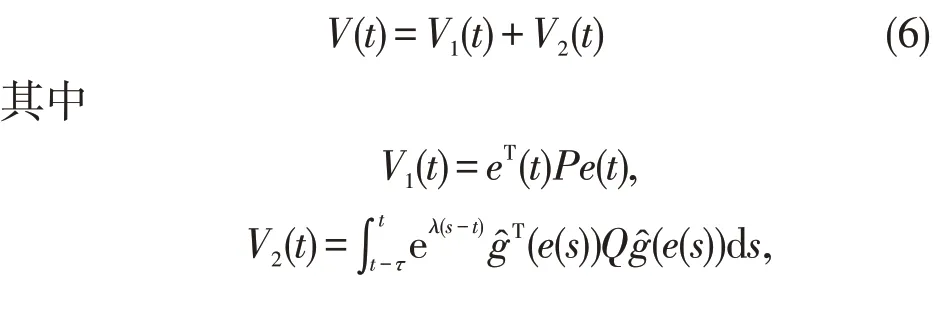
于是，当σ(t)=1,t∈[tk,tk+1)时，可计算Lyapunov 泛函V(t)沿着系统(4)的导数

由引理2，得到

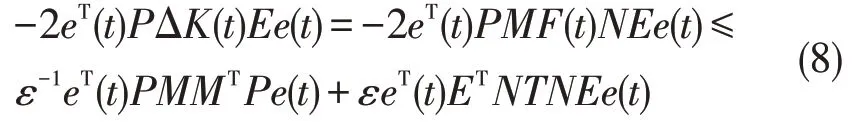
因此，由(7)和(8)得到

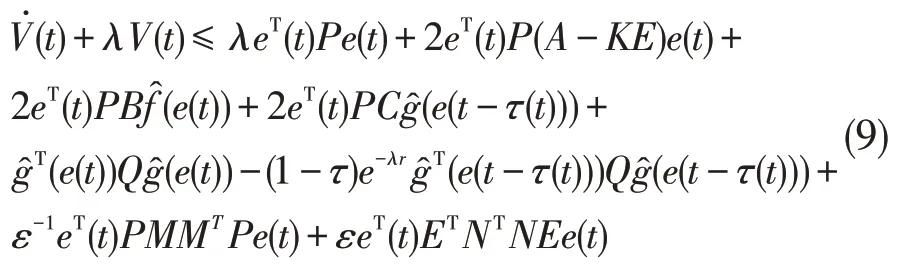
由假设1 和文献[20]中引理3 的结果可得

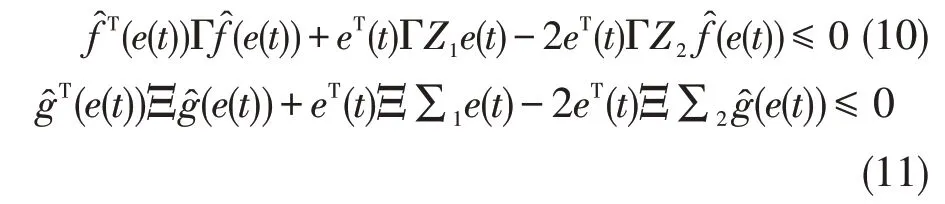
于是，由(9)～(11)得当σ(t)=1,t∈[tk,tk+1) 时，

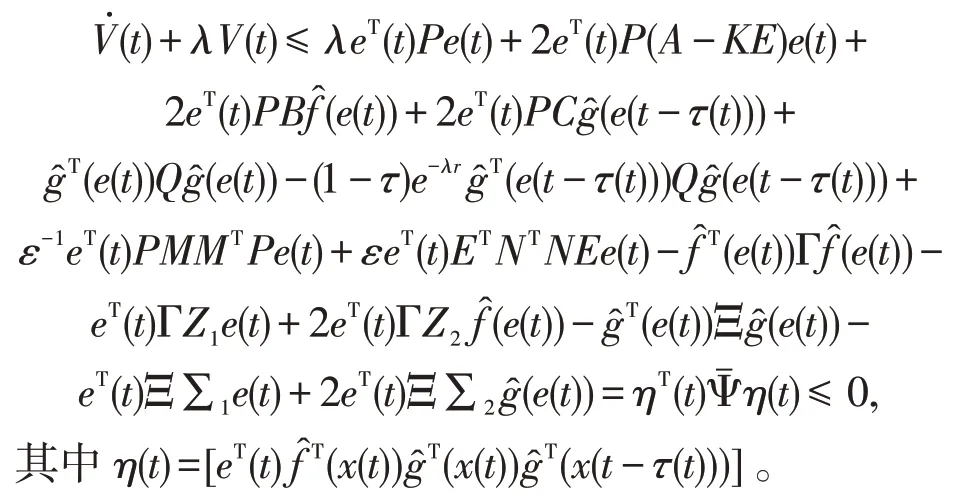
再由条件(5)得到，当σ(t)=1,t∈[tk,tk+1) 时，有+λV(t)≤0,进而V(t)≤，t∈[tk),tk+1。

当σ(t)=2,t∈[tk,tk+1)时，系统(4)改写为

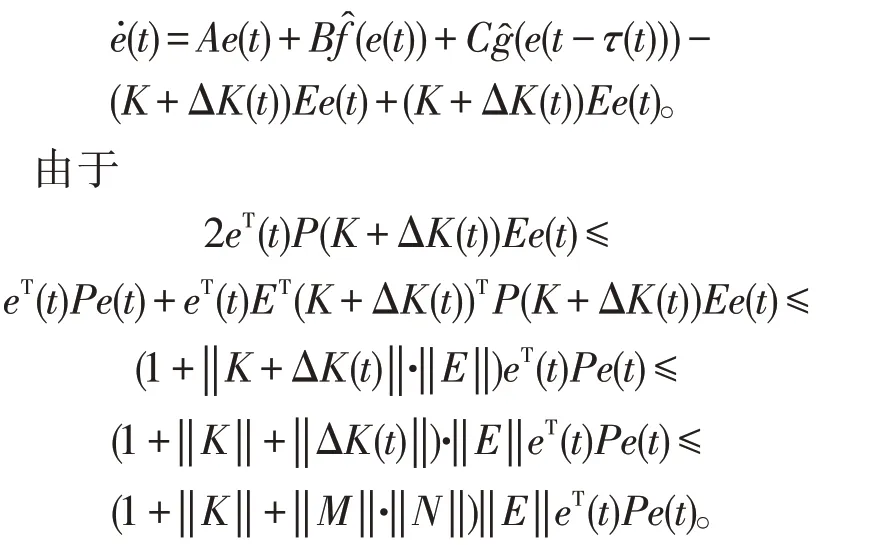
于是，当σ(t)=2,t∈[tk,tk+1) 时，类似于σ(t)=1的情形，由条件(5)可得Lyapunov 泛函V(t)沿着系统(4)的导数满足

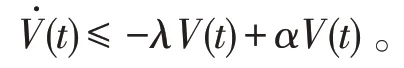
进一步，

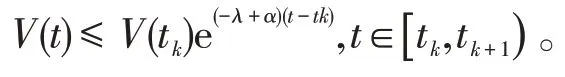
因此，对于系统(4)，t∈[tk,tk+1) 时,有

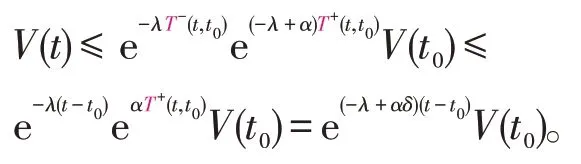
故当δ＜时，由定义1 知，系统(4)是鲁棒全局指数稳定。证毕。

上面的定理1 借助Lyapunov 稳定性和矩阵不等式技巧，给出了间歇型非脆弱状态估计器(2)的存在条件。接下来，我们将通过线性矩阵不等式的可行解表示估计器的增益矩阵。

定理2在假设1 之下，对给定的正数λ，若存在正常数ε，正定矩阵P,Q，正定对角矩阵Γ和矩阵R，使得

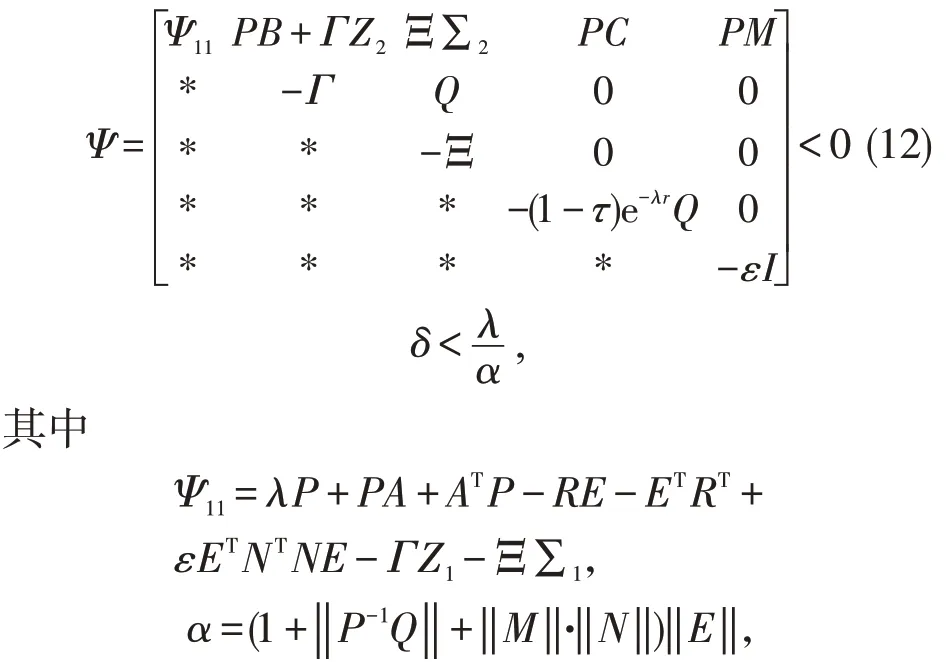
则系统(2)是时滞神经网络(1)的间歇型的非脆弱状态估计器，其中K=P-1R。

证明令R=PK应用Schur complement 引理，则(12)式等价于(5)式，从而由定理1 可得结论成立。证毕。

3 数值举例

该部分将通过数值举例验证所建立结论的可行性。考虑连续型的时滞神经网络(1)，取其系统参数为

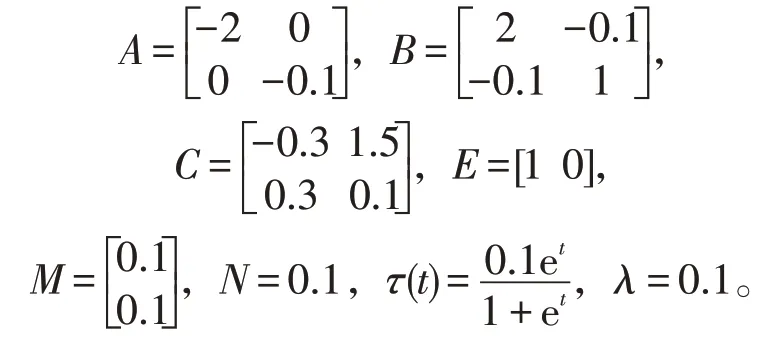
并取激励函数

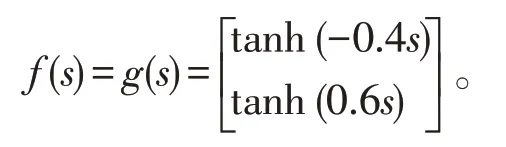
由上面的参数，可得

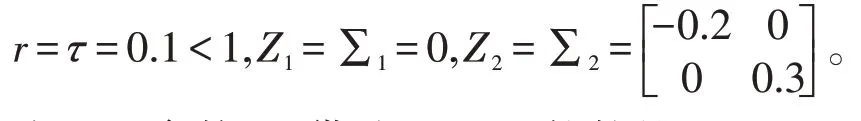
在上述参数下，借助Matlab 软件的Yamip 工具箱求得矩阵不等式(12)的一组可行解为

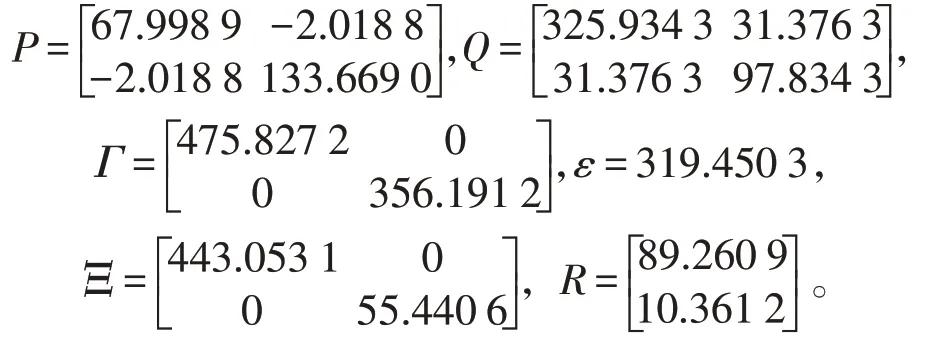
根据定理2，可得控制增益矩阵

因此，当停歇率δ＜0.042 9 时，系统(2)是时滞神经网络(1)的间歇型非脆弱状态估计器。

4 小结

本文针对时滞神经网络模型，设计了间歇型的非脆弱状态估计问题。所考虑的估计器允许间断地工作，并且其控制参数满足范数有界的不确定性。