磁悬浮自动注射器驱动模型设计

吴 芮，刘泽旭，张守京

（西安工程大学机电工程学院，西安 710048）

0 引言

注射器是日常医疗过程中不可或缺的工具，常见的一次性无菌注射器使用是医护人员利用活塞推杆挤压药剂使其通过针管注射入体内。随着科学技术的发展，新的医疗手段也在持续更新，这对注射器在特定环境下的安全、高效和精确以及除医护人员外的使用人员的专业性等方面提出了更高的要求，因此对于新型自动注射器驱动方式的研究也越来越迫切。目前的自动注射器研究主要分为有针和无针2 个方面。

（1）有针注射器。国内对有针自动注射器的研究较为成熟，尤其是在禽类、畜类养殖的疫苗接种及医学检验造影剂注射[1]等方面有多个应用。李开元等[2]设计了一种全自动胰岛素注射器，该装置利用安培力使针头穿刺皮肤、步进电动机推注药剂，可以减小注射痛感、精确控制药液量，但其研究并不深入。英国Goossens 等[3]设计了一种自动针头缩回的注射器，当药剂注射完全后针头自动脱落更换，提高了安全性。浙江大学的叶陈吉[4]设计了一种禽用有针自动注射器，出口流道大于1 mm，且注射过程溶液温度上升为0.04～0.45 ℃，对多数药剂并无影响，适用于多场合、无电源的连续注射。Jafarzadeh 等[5]设计了三相步进电动机驱动的有针自动注射器，通过设计相应控制算法，其注射速度最快可达0.17 mL/s。目前我国市场上的有针注射器多是弹簧或电动机驱动，受弹簧刚度和电动机控制性能影响，存在注射精度低、低速时振动以及冲击较大的问题，在注射要求较高的场合中使用受限。

（2）无针注射器。无针注射器是将注射液通过喷嘴形成高压、高速的喷射流直接注入到皮下、皮内组织的医疗器械，其具有痛感小、吸收快、安全性高的优点，根据驱动方式不同主要分为弹簧动力式、高压气动式、音圈电动机驱动式等[6]。国外对无针注射器的研究起步较早，对驱动原理与结构、喷射流参数、药剂作用效果等方面探究较多[7-9]。英国Weston Medical 以及美国Equidyne 等数十家公司已研制生产出多种无针注射器[6]。国内对无针注射器的研究较少。华中科技大学的彭睿[10]简化了弹簧式无针注射器结构，根据对喷射流模型、药剂扩散的研究得出弹簧刚度应在3 871～4 600 N/m，药剂为球形或半球形扩散。杭州电子科技大学的陈凯等[11]构建了音圈电动机驱动的无针注射器，喷射压力可达18 MPa，其双向可控、压力可调的特点弥补了弹簧式无针注射器的不足。苏州大学陈添禹等[12]设计了一种喷射流速峰值为123.6 m/s 的磁阻式电磁蓄能无针注射器，可以解决机械式无针注射器调节难、体积大和机构复杂的问题。无针注射器虽然优势众多，但要求初始注射时保持高速、高压，对活性低、溶解度小的注射剂并不适用，并且其结构普遍较为复杂，制造成本较高。

本文将洛伦兹力磁悬浮技术引入到注射器中，提出一种洛伦兹力型磁悬浮自动注射器驱动模型。由于模型悬浮驱动，可以消除机械传动有针自动注射器存在的振动、冲击，并且该驱动模型力与电流呈线性关系，控制系统更加简单、控制精度更高。同时，由于不需要将注射液高速喷出，可以适用于多种类型的注射剂与注射环境。

1 驱动原理与结构

1.1 驱动原理

磁悬浮技术可根据驱动原理分成磁阻力型和洛伦兹力型[13-14]，其中洛伦兹力型由于力与电流有较好的线性关系，具有响应迅速、模型简单以及控制精度高的优点。洛伦兹力原理如图1 所示。洛伦兹力表达式为

图1 洛伦兹力原理示意图

式中，f 为洛伦兹力；q为电荷带电量；v 为电荷运动速度；B 为磁感应强度。

由于电流是大量电荷运动形成，洛伦兹力在宏观电流上表现为安培力，安培力表达式为

式中，F 为安培力；I 为电流大小；l 为导线长度。

1.2 结构

本研究基于电荷在磁场中受洛伦兹力作用提出如图2 所示的磁悬浮自动注射器驱动结构原理图，由永磁体、磁轭、线圈、活塞推杆、针筒、外壳、位置传感器、控制器和功率放大器等构成。

图2 磁悬浮自动注射器驱动结构原理图

利用4 个永磁体布置2 个近似均匀而磁感应强度相反的磁场，其中上侧磁场磁感应强度方向向右、下侧磁场磁感应强度方向向左；将一个方形线圈的上下两端导线置于2 个磁场的有效范围内，给线圈通入电流使线圈上端导线电流流出、下端导线电流流入，则线圈受安培力作用；由于线圈上下两端的电流方向相反且磁场方向相反，线圈上下两端导线受安培力大小相等、方向均向上，若通入的电流反向，则线圈受向下的安培力；线圈两侧导线分布宽度大于永磁体宽度，所以两侧导线始终处于磁场的外部而不会受到力作用，确保线圈只能上下直线运动。

将4 个正对的永磁体安装在2 块磁轭上，使模型驱动系统的磁路闭合，更高效利用磁场产生电磁力，并连同针筒组成定子；活塞推杆固定在方形线圈上组成动子，并使线圈上下两端导线在运动过程中始终处于有效磁场范围内；当给线圈通入直流电后活塞推杆会产生位移，通过位置传感器实时采集活塞推杆位置信号，经过控制器分析运算后输出控制电流；控制电流再经过功率放大器放大后输入到线圈进行驱动，从而完成注射工作，整个驱动系统为闭环控制系统。由于该模型存在永磁体产生的稳恒磁场，为避免注射器实际使用及存放中与环境或其他设备产生电磁干扰，需要利用隔磁外壳（如铝壳）将线圈、永磁体和磁轭包裹，防止磁场相互耦合对模型精度产生影响。

该结构下通过控制电流使线圈直接带动推杆悬浮运动，整个过程不存在机械传动，没有刚性冲击与振动，与弹簧、电动机驱动的注射器相比注射过程更加平稳，驱动结构磨损更小。同时，驱动力由控制电流决定，针对不同注射环境的调节更加便捷、迅速。

2 数学模型建立

2.1 受力分析

模型整体受力分析图如3 所示。动子运动过程中会受到电磁力、摩擦力、重力以及推杆活塞的轴向压力，动子所受合力F合表达式为

式中，N 为线圈的匝数；I1、I2为线圈上、下端电流，大小相等、方向相反；L 为磁场中线圈的有效长度；B1、B2为上、下磁场的磁感应强度，大小相等、方向相反。

图3 模型受力分析图

在该模型中稳恒磁场由永磁体提供，若忽略漏磁磁阻，其磁感应强度B1、B2大小可以由气隙磁感应强度表达式计算：

公式（6）仅为近似计算使用，工程实际计算磁感应强度B 较为复杂，通常采用电磁有限元软件进行仿真计算。

活塞推杆在运动过程中处于悬浮状态，除针筒的径向支撑外几乎无刚性接触。本文将活塞推杆在运动过程中受到的摩擦力f 与轴向压力FN的共同作用看作是系统的一个阻力Fd，则系统所受合力表达式可简化为

2.2 系统运动方程

将活塞推杆与线圈等效为一个质量块，根据公式（7）和牛顿第二定律系统可得动子运动微分方程为

式中，M 为系统总质量；x¨为系统加速度。

将公式（4）、（5）代入公式（9），得到系统整体的运动方程为

式中，V 为注射量；s 为针管截面积；h 为活塞推杆行程；r 为针管半径；t 为注射时间。

3 电磁有限元分析

3.1 电磁场建模与分析

本文设计的磁悬浮自动注射器模型由永磁体提供稳定磁场使通电线圈在安培力作用下带动活塞推杆运动，对模型磁场的分析可以为后续驱动参数的选择和控制过程提供合理依据。前期查阅资料发现，对永磁体磁场的建模和理论分析较为复杂，且忽略了材料非线性特性、漏磁等[15]，因此本文采用有限元软件对模型电磁场进行分析，其计算精度高，适合模型初期的设计。

根据磁悬浮技术的驱动原理，采用二维平面静态磁场有限元模型进行分析，模型为Plane13，为四边形13 节点单元。定义模型材料参数如下：空气相对磁导率为1.000；永磁体材料选钕铁硼，其剩磁为1.17 T，内禀矫顽力为844 000 A/m，相对磁导率为1.103；线圈匝数为200 匝，相对磁导率为1.000；磁轭相对磁导率为4 000。模型有限元网格如图4 所示。

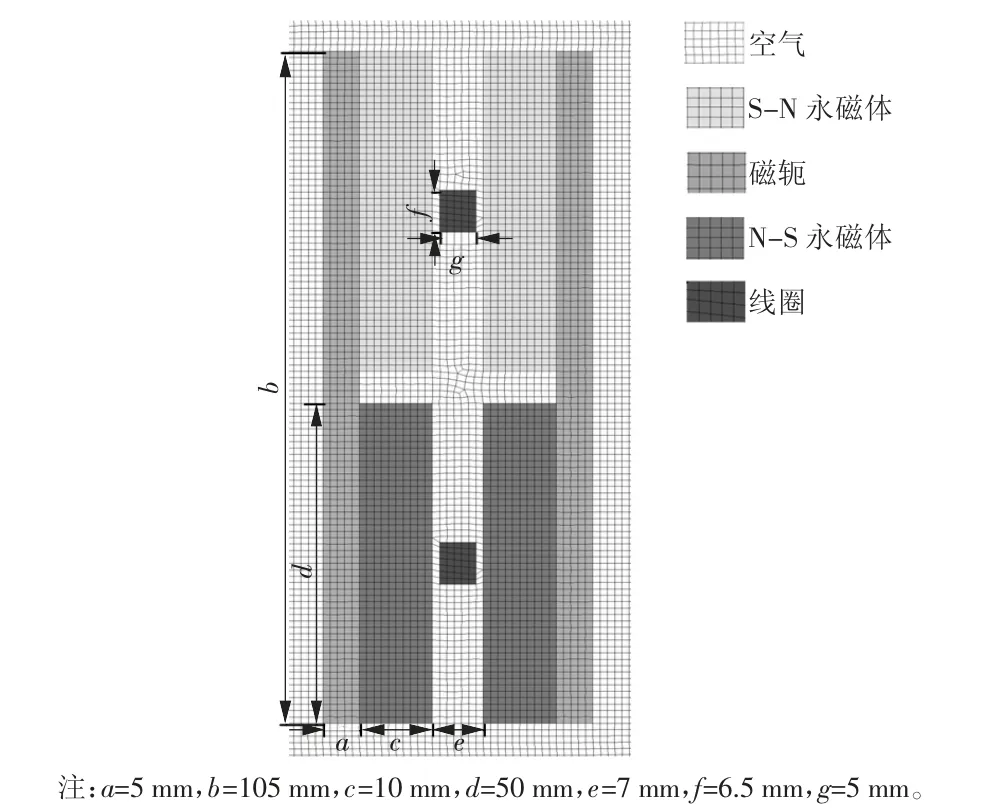
图4 模型有限元网格

对磁场有限元模型求解后，驱动器磁场有限元仿真结果如图5 所示。由图5（a）可看出，磁力线沿磁轭以及2 个永磁体正对的气隙处闭合，漏磁较少；由图5（b）可看出，2 组永磁体正对区域内的磁感应强度较大，且分布较为均匀。

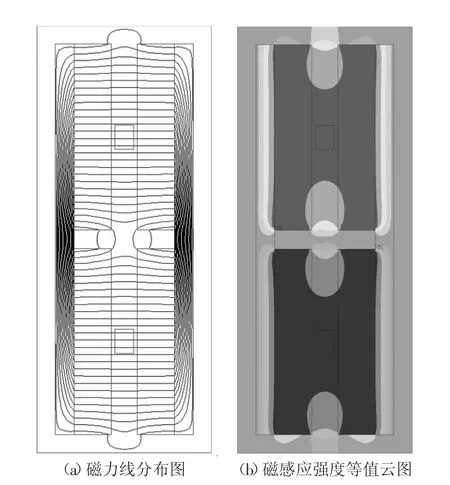
图5 磁场有限元仿真结果

定义模型最下侧为“零”位，模型气隙中部区域的径向磁感应强度变化曲线如图6 所示。可以看出模型磁感应强度在上下永磁体中各有一段平稳期，磁感应强度大小稳定在0.83 T。将注射器行程设计在该区域内即可驱动活塞推杆完成注射动作。

图6 径向磁感应强度变化曲线

给线圈通入1.5 A 电流，根据ANSYS 软件的电磁力仿真结果，轴向有磁场对线圈产生的向上单位长度安培力FY/L=393.30 N/m；径向有永磁体对线圈产生的向左单位长度磁阻力FX/L=-0.021 43 N/m，较小，可忽略。

3.2 驱动力分析

根据GB 15810—2019《一次性使用无菌注射器》[16]，可知普通注射器侧向摩擦力最大为3 N，轴向最大压强为0.3 MPa，注射要求最大初始力为30 N，假设喷口出口半径为2.1×10-4m，则需要的最大驱动力为

式中，F需为需要的最大驱动力；F初为最大初始力；P轴为轴向最大压强；S 为喷口截面积。

根据上一节的计算，假设磁场中导线有效长度为0.1 m，本文设计的磁悬浮自动注射器驱动模型可提供的最大驱动力为

式中，F驱为最大驱动力；l 为线圈导线有效长度。

由此计算可知当给线圈通入1.5 A 电流时，本模型产生的驱动力完全可以驱动活塞推杆完成注射动作。

4 结语

本文基于线圈在磁场中受洛伦兹力提出了一种磁悬浮自动注射器驱动模型，模型结构简单，可实现程序化控制且系统线性度好。通过ANSYS 软件对模型磁场、电磁力进行分析，结果显示磁场均匀稳定，磁感应强度保持在0.83 T，电磁驱动力可达39.33 N，能满足注射要求。本驱动模型将为消除机械传动类注射器摩擦、振动和冲击的研究提供新的思路和方法，但目前在高精度控制系统的设计以及实物实验方面还有待完善，本文提出的理论与仿真结果可为下一步的研究提供理论参考。