基于超宽带生物雷达的动态杂波干扰抑制技术研究
2021-11-03许兆坤王昭昳白思源薛慧君
许兆坤,王昭昳,白思源,张 杨,薛慧君
(空军军医大学军事生物医学工程学系,西安 710032)
0 引言
生物雷达概念的提出源于常规雷达技术在生命探测领域的应用,特指探测生命体的雷达。生物雷达发射电磁波,穿透衣物、墙壁、废墟等非金属遮挡或障碍物,非接触地获取人体目标呼吸、心跳等生理信息[1-3]。与红外、声波、激光探测技术相比,生物雷达探测人体生命体征不受环境温度、噪声以及废墟孔径等影响,是国内外广泛应用的生命探测技术[4]。超宽带(ultra-wide band,UWB)生物雷达因其具有较强的穿透性和抗干扰能力、能准确捕获目标距离信息等特点,更适用于地震、塌方等灾后搜救[5-8]。
地震发生后,大多会伴随大风、雨雪等恶劣天气,导致生物雷达探测区域内植物(枝干、树叶等)发生不规则抖动。由于生物雷达探测原理是检测人体呼吸等引起的体表微动(微动幅度较小,多为毫米级)[9],一旦植物抖动引起的动态杂波被生物雷达接收,势必对生物雷达探测造成干扰。一些学者曾开展了在动态杂波干扰下对人体目标的探测研究,张芫蓓等[10]对由强反射障碍物引起的非静态杂波展开研究,提出了一种基于双源IR-UWB 生物雷达的强反射杂波抑制方法,利用2 种不同中心频率的雷达天线,通过等效时间采样和分时复用技术同时对目标进行探测,再配合自适应杂波消除算法,能够较好地抑制不同场景中的强反射杂波干扰。Hosseini 等[11]将时变系数傅里叶级数模型作为拟合模型,采用基于带限信号的无条件标准正交算法对回波信号进行处理,抑制雷达回波中非平稳动态杂波的干扰,得到稳定的呼吸信号。而实际搜救中植物晃动幅度可能大于人体呼吸微动,且植物晃动引起的动态杂波干扰可能包含呼吸频段,因此,基于能量识别和时频滤波等的探测方法准确率不高。
基于本课题组前期的研究,当人体静止时,呼吸引起的胸腹部微动信号在生物雷达回波中处于固定位置,受人体胸腹部厚度或雷达辐射横截面积的影响,人体位置处相邻距离单元都能够检测到呼吸信号[12]。考虑到人体呼吸信号具有准周期特性而树叶抖动等引起的非静态杂波大多是不规则的随机信号,本研究从二者信号的特性差异入手研究动态杂波干扰下的人体目标识别方法。基于小波变化具有良好的时、频局部化和多尺度分辨特性,可同时对一组信号进行时、频分析[13],以及信息熵能够表征系统状态的复杂度[14],本文拟将小波变换和信息熵结合,采用小波信息熵算法,通过计算不同频段能量分布的复杂程度识别动态杂波干扰下的人体目标。
1 UWB 生物雷达系统
UWB 生物雷达系统探测原理如图1 所示。生物雷达包含1 个发射天线和1 个接收天线,中心频率为500 MHz。脉冲发生器产生重复频率为128 Hz 的脉冲触发信号,触发信号通过发射天线照射人体,携带人体生理信息的生物雷达回波信号被接收天线接收,再经采样、信号积累、滤波放大等,送到后端计算机系统等待进一步处理,其中,采样器采样频率为64 Hz,采样点数为2 048。生物雷达探测“时窗”为60 ns,电磁波在真空中传播速度为3×108m/s,对应最远探测距离为9 m。

图1 UWB 生物雷达系统探测原理图


2 信号处理算法
2.1 信号预处理
由于复杂探测环境和UWB 生物雷达系统自身的影响,生物雷达天线接收到的反射电磁波信号会同时包含目标反射信号、多种噪声以及静态(或动态)杂波干扰。为了消除探测环境中的噪声和杂波干扰,需要对生物雷达回波信号进行预处理。生物雷达回波信号预处理算法流程如图2 所示。

图2 生物雷达回波信号预处理算法流程图
具体如下:
(1)距离累积:由于送入计算机系统的生物雷达回波信号数据量非常大,严重影响后期信号处理速度。本文根据人体微动信号在快时间维度(距离维度)临近单元多个点信号具有很大的相关性,在不影响有用信息提取的前提下,沿距离维度对生物雷达回波信号数据RM×N进行距离累积,将信号传输距离上的采样点从2 048 压缩到200。
(2)归一化:生物雷达发射的电磁波在穿透障碍物和自由空间传输过程中存在能量衰减,使得生物雷达回波信号的信噪比降低。为了增强生物雷达天线远端人体目标信号的幅值、提高生物雷达回波信号的信噪比,本文沿着慢时间维度(探测时间维度)对距离累积后的数据矩阵进行归一化处理。
(3)去基频:生物雷达回波信号中包含了天线直达波和墙体反射回波以及探测环境中其他静止物体反射的静态杂波,这些回波信号会形成很强的背景杂波,从而淹没人体微动信号。首先可通过选择信号起始位置规避天线近处的直达波干扰,再利用“静态杂波杂乱无章、能量恒定、人体微动信号近似准周期性信号”的特性,通过平滑滤波减去生物雷达回波信号中不同距离点时域信号的均值去除部分静态杂波。
(4)自相关:生物雷达工作过程中不可避免会产生高频噪声,从而降低生物雷达回波信号的信噪比。基于人体呼吸信号窄带准周期性的特点,采用自相关算法进一步增强人体信号规律性的同时,去除高频噪声,提高生物雷达回波信号的信噪比。
2.2 小波变换
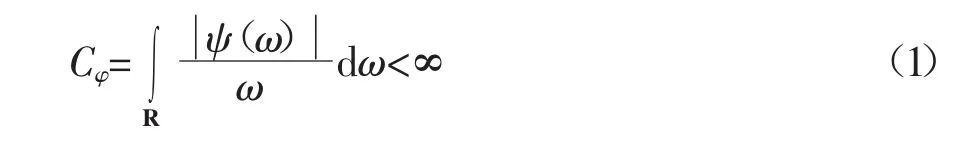
采用小波变换对信号进行处理的过程中,小波函数的选取是首要环节,不管选取哪种小波函数,ψ(t)都要满足以下条件:式中,Cφ指ψ(ω)在函数空间中的积分结果;ω 为时域小波函数变换在复频域中所对应的频率;令L2(R)为实平方可积函数空间,ψ(t)∈L2(R),ψ(ω)为ψ(t)的傅里叶变换,且当ω=0 时,ψ(ω)=0。
上述小波函数ψ(t)经过平移和伸缩后可获得小波基函数,在预先设定尺度因子和平移因子情况下,经伸缩平移得到的小波簇ψa,τ(t)如下所示:

式中,t 为时间;a 为尺度因子,反映了特定基函数的尺度;τ为平移因子,表示小波沿t 轴平移的位置。其中a,τ∈R,a≠0。
对于信号f(t)∈L2(R)空间的连续小波变换(continuous wavelet transform,CWT),可定义为函数f(t)在不同尺度a 和τ 对应的小波簇ψa,τ(t)的内积:+∞

2.3 小波信息熵算法
为了更好地表达小波信息熵算法,假设预处理之后的慢时间维度信号为Xτ(t)(τ=1,2,…,200),信号Xτ(t)的DWT 定义如下:

DWT 提供了一种无冗余的信号表示形式,其输出值为小波序列的系数Cj(k),这里的小波序列系数Cj(k)不仅能够提供信号的相关信息,还能对不同尺度、不同时刻的小波能量进行估计。假设信号Xτ(t)沿时间方向的采样点为X={x0(n)},其中,n=1,2,…,N,N 为信号采样点最大值200,如果离散二进制小波能对整个分辨力等级进行分解,那么信号Xτ(t)的小波变换可表示为
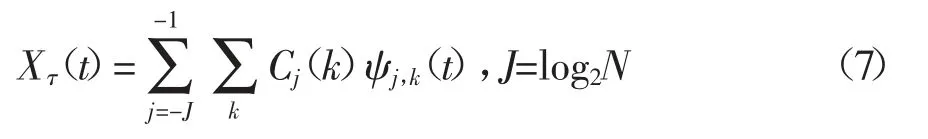
由于小波簇ψj,k(t)为空间L2(R)的正交基函数,并且其能量概念的引出方式与基于傅里叶变换的能量概念一致,信号Xτ(t)的小波序列系数可由公式Cj(k)=

为了观察每个参数的瞬时变化,对生物雷达信号进行加窗分帧处理,设分帧的窗宽为L,对于每一帧i(i=1,2,…,NF,NF=N/L)的信号值为所加时间窗的中心点的信号值。在二进制离散小波分解中,子带j下的小波系数的个数应为前子带j-1 下的小波系数的一半,因此,加窗分帧的最小窗宽要保证每一子带至少保留一个小波系数。这里每一子带j 下小波能量用该子带下各个分帧平均能量的总和表示,即

3 实验及分析
3.1 实验设计
为了探究小波信息熵算法在动态杂波干扰下识别人体目标的能力,本文以UWB 生物雷达为探测平台,通过线性模组往复运动模拟人体呼吸,通过电风扇吹植物,使其枝叶抖动模拟灾害现场的风吹草动。其中,线性模组往复运动频率为0.2 Hz、运动幅度为6 mm,植物放置于线性模组和生物雷达中间,根据风扇与植物距离的变化,探测实验分3 组进行,实验场景如图3 所示。每组实验重复10 次,线性模组模拟人呼吸,电风扇均调到最大挡位,通过调整电风扇与生物雷达的实际距离改变生物雷达回波信号的信杂比(signal to clutter ratio,SCR)。

图3 模拟动态杂波干扰下UWB 生物雷达探测人体目标实验
3.2 实验结果与讨论
3.2.1 动态杂波特征分析
任取图3(a)中抖动植物对应距离点的动态杂波信号和线性模组的生物雷达回波信号,对二者预处理后的2 路生物雷达回波信号进行快速傅里叶变换,频谱分布结果如图4 所示。由于人体呼吸信号频率为0.2~0.7 Hz,为了更好地观察频谱分布,舍弃高频部分,频谱范围截取0~10 Hz。由图4(a)可以看出植物抖动引起的动态杂波干扰信号频谱成分比较复杂,且包含呼吸信号频谱成分。图4(b)显示线性模组生物雷达回波信号中同样也有很多频谱成分,但与动态杂波干扰信号相比,高频部分的频谱幅值相对较低,主要频谱分布集中在低频0.2 Hz,与线性模组的设置运动频率相符。

图4 植物抖动引起的动态杂波干扰和线性模组的生物雷达回波信号预处理之后的频谱分布结果
3.2.2 SCR 分析

上述3 种实验场景中,随着电风扇与生物雷达距离变小、电风扇与植物夹角缩小,电风扇与植物的相对距离逐渐变小,会引起植物不规则抖动幅度的变化。为了探究电风扇位置变动对生物雷达回波SCR的影响,通过计算有用信号与杂波干扰信号的能量比,对3 组实验回波数据进行SCR 分析:式中,P(n)为生物雷达回波信号在不同距离点的能量幅度;k 为被测目标的距离点。3 组实验生物雷达回波信号SCR 统计结果见表1。由表1 可知,当电风扇距离生物雷达3 m、与植物夹角50°时,生物雷达回波信号平均SCR 为-20.950 dB;当电风扇距离生物雷达3 m、与植物夹角30°时,平均SCR 为-24.438 dB;当电风扇距离生物雷达2 m、与植物夹角10°时,平均SCR 为-27.806 dB。综上,可得出:电风扇与植物的距离越近,对植物产生的干扰越强,SCR 就越低。

表1 3 组实验生物雷达回波信号SCR 统计结果 单位:dB
3.2.3 结果与讨论
使用小波信息熵算法对图3 中的生物雷达回波信号进行处理,以传统的自适应谱线增强[15]和能量累积[16]算法作为对比方法,信号处理结果如图5所示。图5(a)和(b)为图3(a)的自适应谱线增强和能量累积算法的识别结果,图5(a)显示距离生物雷达4 m 处出现较明显的波动信号,根据先验知识,可判断此波动信号为有规律往复运动的线性模组。由于环境中的动态杂波干扰以及这种干扰在探测区域的多径反射,在线性模组后1 m 的距离出现较强波动信号,凭经验盲判,5 m 位置会出现虚警。图5(b)中距离生物雷达4 m 处出现明显能量谱峰,此处为线性模组,而在约5 m 处出现最大能量谱峰,易造成误判。图5(c)为图3(a)的小波信息熵算法的识别结果,可见在距离生物雷达4 m 处熵值出现最低值。根据上文分析可知,生物雷达回波信号中线性模组的反射信号频谱成分单一,是窄带周期信号,该信号经过小波变换后在不同尺度的能量分布与植物枝叶抖动形成的动态杂波分解后的能量相比分布更加规律,因此线性模组运动信号的小波熵值比动态杂波的小波熵值更低,由此可判断距离生物雷达4 m 处为线性模组。同理,图3(b)和(c)的自适应谱线增强算法和能量累积算法的识别结果[如图5(d)和(e)、图5(g)和(h)所示]都无法准确识别线性模组位置,且随着SCR 降低,2 种对比方法识别结果中虚警率逐渐增加,而图3(b)[如图5(f)所示]和图3(c)[如图5(i)所示]的小波信息熵处理结果不受环境SCR 影响,可准确识别出运动的线性模组。

图5 3 组实验场景生物雷达回波信号数据的识别结果
4 结语
UWB 生物雷达系统探测人体时,探测环境中风吹草动引起的动态杂波会对生物雷达探测造成干扰。传统的时域和频域分析方法难以在动态杂波干扰下准确探测人体。本文通过分析线性模组往复运动模拟的人体呼吸信号与植物不规则抖动引起动态杂波干扰信号的频谱成分复杂度的差异,提出基于小波信息熵的动态杂波干扰下的人体目标识别算法。实验中,线性模组往复运动模拟人体呼吸,电风扇吹植物引起植物不规则抖动模拟动态杂波干扰,采用小波信息熵算法对生物雷达回波信号进行处理,并以传统的自适应谱线增强算法、能量累积算法作为对比研究算法。从结果及分析可以看出,传统的自适应谱线增强算法和能量累积算法以能量为分析对象,易受探测环境动态杂波及其多径反射效应等引起的干扰影响而形成虚警。小波信息熵算法以频谱成分的复杂度为分析对象,对植物不规则抖动引起的动态杂波干扰和背景噪声具有良好的抑制作用。可见,该探测场景下小波信息熵算法能准确识别人体目标。而由于小波信息熵算法是基于有用信号与干扰信号频谱复杂度的差异性对人体目标进行识别,若干扰信号频谱复杂度近似于人体呼吸信号,该算法无法准确探测目标信号,还需做进一步的特征识别。
