农业机械测量中误差修正研究
2021-11-03山西省农业机械发展中心陈壮
山西省农业机械发展中心 陈壮
1 概述
在农业机械试验鉴定中,风速仪是一种经常用到的仪器。为了保证测量的准确性,仪器需要经法制计量部门或法定授权组织检定或校准,经过校准的仪器需要再经过实验室人员确认,满足检测要求才可投入使用。风速仪的校准证书给出两组数据,一组为标准值,一组为测量值,并没有给出修正信息,且经过计算仪器误差大,影响了仪器测量的准确性,进而影响农机鉴定结果的准确性,因此,面对这一问题,需要对校准结果进行修正,研究修正的方法及修正后的误差关系,从而提高仪器测量精度,保证农机鉴定结果的准确性。仪器设备经检定/校准结果产生的修正信息包括修正值、修正因子、修正曲线[1]。本文基于最小二乘法,利用工具MATLAB,拟合出修正曲线与误差修正公式,并对拟合误差和阶数的关系进行理论研究,旨在为仪器校准结果修正提供计算方法,提高仪器测量精度,使农机鉴定结果更加精确。
2 最小二乘法原理
最小二乘法是解决曲线拟合问题最常用的方法。它通过最小化误差的平方和寻找数据的最佳函数匹配[2-4]。利用最小二乘法可以简便地求得未知的数据,并使这些求得的数据与实际数据之间误差的平方和为最小。它的基本思路是选择估计量使模型输出与实测输出之差的平方和达到最小[5]。
有一组数据(xi,yi)(i=0,1,2...,n),设多项式为f(x),令:

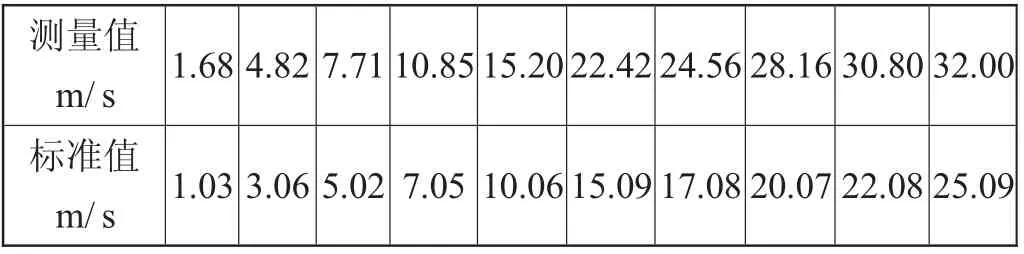
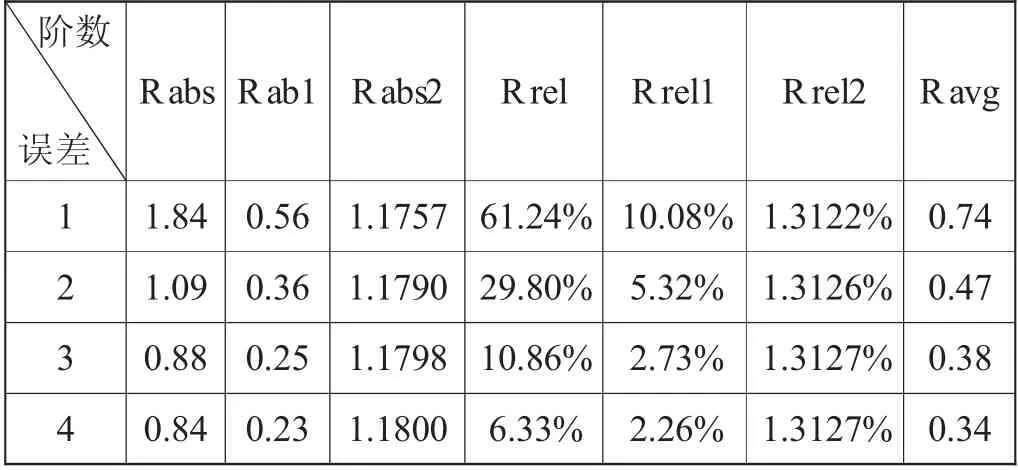
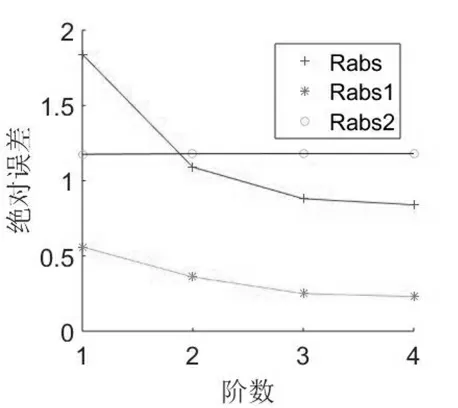
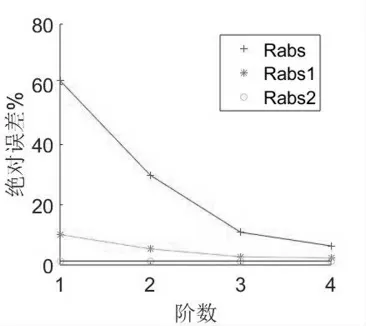
式中:f(x)为拟合函数,ak是待定系数,(k=0,1,2,...,m 式中a0.a1,a2...,ak为待求的未知数,k为多项式最高次幂,因此该问题转化为求方程的极小值问题。polyfit函数是MATLAB中用于曲线拟合的一个函数,其数学基础是最小二乘法曲线拟合原理,因此利用MATLAB可以解决这一问题。 在农业机械鉴定中风速是一个很重要的参数,大纲DG/T006-2019《微耕机》中,驾驶员耳位噪声测试要求风速不大于5 m/s;大纲DG/T015-2019《玉米收获机》耳位噪声测试中要求,配置简易驾驶室或无驾驶室机型测试时,离地表1.2m处的平均风速应不大于3m/s,如果风速测量不准会影响鉴定结果的准确性。根据F30J型智能热球式风速计校准结果(校准证书编号:JZFB202000834)可得知表1数据: 表1 仪器校准结果 仪器校准结果的好坏通常可以用误差来表达。误差可以用绝对误差和相对误差来表示:绝对误差是测量结果与真值之差;相对误差是绝对误差和真值的百分比率[2]。当测定值大于真值时,误差为正,表明测定结果偏高;反之,误差为负,表明测定值偏低。 根据表2计算可得:绝对误差最大值为8.72,平均值为5.25,标准差2.70;相对误差最大值为63.1%,平均值为47.89%,标准差1.01%;均方根误差5.92。可见误差太大已经影响了仪器的准确性,需要修正。设测量值为x,标准值为y,现需要拟合出x和y之间的函数关系,即误差修正公式。 表2 仪器校准误差 对于一个实际的曲线拟合问题,必先将实测值用平滑线散点图描出,观察其分布趋势,再结合专业知识选取最接近的函数关系式来拟合;本文应用最小二乘法多项式拟合,利用MATLAB软件可方便快捷找出对应关系,实现仪器的误差修正,分析拟合阶数对拟合误差的影响。 误差修正公式表示仪器的测量值x与标准值即实际值y之间的关系,随着拟合阶数的不同误差修正公式也有不同的表现形式。MATLAB求修正公式核心语句为:p=polyfit(x,y,n),阶数n不同时拟合的校准曲线如公式所示: 当阶数n=1时,误差修正公式为: 当阶数n=2时,误差修正公式为: 当阶数n=3时,误差修正公式为: 当阶数n=4时,误差修正公式为: 误差修正公式的应用:农机试验测量时,仪器的测量值即读数为x,由于仪器有误差,可代入修正公式求得y,即为这次测量的实际值。 从公式可知:阶数越大,方程越复杂,计算也越复杂,但拟合后的效果还不明确,需进一步研究。 为了更精确的检验与分析拟合误差,定义拟合误差度量为: 式中,f(xi)表示拟合函数,yi表示原函数(标准值),Rabs表示绝对误差的最大值,Rabs1表示绝对误差的平均值,Rabs2表示绝对误差的标准差,Rrel表示相对误差的最大值,Rrel1表示相对误差的平均值,Rrel2表示相对误差的标准差,Ravg表示均方根误差。表3表示阶数n不同时拟合后误差的大小: 表3 拟合后误差 从表3和图1可知:(1)随着阶数n的递增,Rabs、Rabs1、Rrel、Rrel1、Ravg都是逐渐减小的趋势,说明拟合后的绝对误差、相对误差和均方根误差均是在减小,因此修正后的值也越准确;(2)随着阶数n的递增,曲线变得更加平缓,说明Rabs、Rabs1、Rrel、Rrel1、Ravg减小的幅度也在减小,因此阶数越高误差减小的越不明显;(3)随着阶数n的递增,Rabs2、Rrel2两个标准差从图上看是一条直线,从表中看是递增的,但递增的幅度非常小,可以忽略不计,认为他们是不变的,说明拟合后的数据偏离平均值的大小即离散程度是不变的,证明算法的稳定性。 图1 拟合误差随阶数的变化 本文以最小二乘多项式拟合为基础,针对农业机械试验鉴定中风速仪误差过大的问题,进行曲线拟合,给出误差修正方程,并对拟合阶数和拟合误差的关系进行研究,综合本文内容,得到以下结论: (1)阶数越高,曲线越平滑,拟合误差越小,修正后仪器数据越准确。 (2)标准差与拟合阶数没有太大关系,无论低高次拟合数据的离散程度不变。 (3)阶数越高,误差减小的幅度越小,计算越复杂,越不利于现场换算,因此建议在满足测量要求的前提下,尽量做低次拟合。
3 实施应用及分析
3.1 风速计校准结果及分析

3.2 误差修正



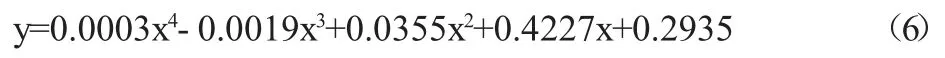
3.3 拟合误差分析研究
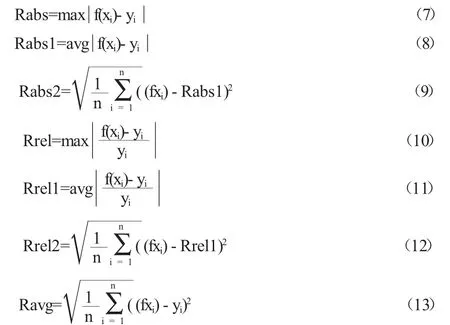
4 结论与建议
