基于Bayes估计的民航维修人为差错评估技术探究

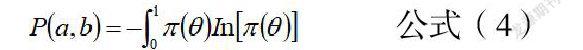
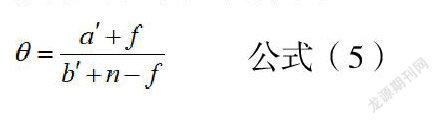
摘要：本文将基于Bayes（贝叶斯）评估方法入手，在了解该算法的基本原理之后介绍了各种人为差错的数据来源;再阐述了贝叶斯技术在民航维修人为差错评估中的应用方法，并结合应用实例进一步介绍了该评估方法的使用效果，希望为降低误差发生率提供支持。

关键词：Bayes;民航维修;人为差错

前言：人为差错是指工作人员出现与质量标准、工作目标相偏离的行为。在民航维修中，人为差错不可能完全杜绝，但是考虑到飞行器属于高精尖设备，任何误差的出现都有可能造成严重后果，所以必须要对民航维修的认为差错问题展开分析，Bayes技术的出现有效解决该问题，值得关注。

1.Bayes的基本原理以及人为误差的来源

1.1Bayes基本原理

贝叶斯评估是目前学术界一种先进的评估手段，该方法主要在设定待估算参数的“先验分布”之后，该先验分布可以由工作人员的经验以及历史采集的数据来确定，根据先验分布结果以及相关数据计算出后验分布情况，而利用后验分布则可以对各种可能出现的未知现象展开评估。与传统的误差评估方法相比，贝叶斯不仅能够涵盖各类样本信息，也能对先验信息进行挖掘、分析的基础上，使原本复杂的信息量化，通过拓展数据的分布范畴来保证先验分布效果，所以最终的评估质量能够得到保障。贝叶斯推理的问题是条件概率推理问题，这一领域的探讨对揭示人们对概率信息的认知加工过程与规律、指导人们进行有效的学习和判断决策都具有十分重要的理论意义和实践意义。

在本次研究中，本文假设带估计的民航维修人为差错概率为θ，在连续分布的随机变量下，贝叶斯的计算方法如公式（1）所示。

在公式（1）中，π（θ）为θ的先验密度函数;π（θ|x）代表θ在x条件下的条件密度函数;w为参数空间;L（x|θ）为样本似然函数，在人为维修差错概率给定的情况下发生失效的分布情况;π（θ|x）代表后验分布的密度函数。

在运用贝叶斯评估方法期间，其中需要先针对每个信息源构造前分布方案，在对随机数据标量进行估计的基础上，确定信息源后;一般在计算人为误差期间，假设整个维修过程中存在n个信息源，在每个信息源赋值均为可读取的情况下，并统计其中的验算结果。

1.2人为差错的数据来源

1.2.1通用数据

通用数据体现了评价行为形成因子情况，要求在差错分析中能针对行为形成因子来对各类人为差错概率进行标定。在贝叶斯算法下，通过整合现场人为误差以及通用数据后，当现场数据数量较少时，则要避免现场数据被淹没，所以针对这种情况，通过在贝叶斯算法中开展关于认知可靠性与差错的分析能够提供人为差错数据以及任务场景，这也是贝叶斯需要重点实现的内容。

1.2.2仿真技术

考虑到民航维修工作的复杂性，为了能够最大限度上提高误差控制能力，相关学者开始运用计算机仿真技术对人为差错进行控制，但是因为仿真技术的精准度无法得到保证，因此在数据仿真过程中容易造成误差。

2.贝叶斯算法的应用流程

2.1确定先验分布

在计算先验分布期间，主要是利用估算方法来计算出人为差错的分布情况，其中的关键技术步骤包括：

步骤一：通过设定分布族为先验分布族，期间假设民航维修的次数为n次，其中发生差错的次数为f次，此时维修的认为差错概率满足二项分布的要求。针对这种情况，按照貝叶斯算法可先在（0，1）的区间内均匀分布先验数据，在确定其满足先验分布的基础上，共轭先验分布族可以按照Beta的算法分布，此时基于Beta的函数分布模式可以按照公式（2）进行验算。

     公式（2）

在公式（2）中，a与b分别代表Beta的分布参数情况;代表Beta函数。

步骤二：相关学者认为维修过程中人为误差的发生率为5%[1]，在本次研究中采用5%为差错的中值。在这种情况下，按照贝叶斯先验分布类型，验算估算法确定通用数据的先验分布情况。为了实现这一目标，可按照公式（3）展开运算。

2.2贝叶斯先验分布参数的计算

考虑到民航维修差错的先验信息来源复杂，在对各种人为差错数据展开分析后，结合统筹数据计算人为差错发生率。在这种情况下，因为上数据本身就有样本特征，在海量数据处理过程中可借助仿真模

型来判断各个数据之间通用性，在假设的情况下，假设分布参

数a与b的仿真模型如公式（4）所示。

在开展贝叶斯先验分布参数计算中，在公式（4）的求导过程中，通过确定一个使达到最大的极值即可。

2.3确定后验分布

在后验分布中可以按照贝叶斯定义，按照样本偶然系数，并根据Beta分布方法，使以及后，選择Beta的分布中间值进行贝叶斯估算，则估算结果如公式（5）所示。

3.实例分析

3.1民航维修人为误差的项目背景介绍

某民航公司的维修任务达到150次/月，维修工作中会因为操作不规范而导致维修质量问题。根据公司提供的维修记录，截至2020年，因为技术原因所造成的维修差错概率均值为3.1×10，根据这组数据计算出Beta分布函数的分别为：a'=2.845、b'=628.03，在将数据代入到公式中之后，计算出贝叶斯θ=4.45×10，按照这一数据可以认为案例民航维修人员在维修期间，因为技术问题而造成的差错概率为4.45×10。在这种情况下，假设不使用先验信息，单纯采用传统的最大似然估计法，选择相同的数据展开计算后，则计算出失效概率为8.0×10，由此可见，贝叶斯定义方法能够进一步降低失效概率发生率。

2.2利用现场数据进行检验

针对民航公司的实际维修部记录，统计该公司因为技术问题而造成的维修误差概率均值达到了6.3×10，在将运算数据与实验结果展开对比后，根据现场数据以及贝叶斯的估算结果，证明两个数据在内容上十分接近，这一结果证明了该方法在评估民航维修人为误差管理中发挥着重要作用。

结束语：

在估算民航维修人为差错结果中，采用贝叶斯估算方法具有可行性，该方法的计算结果与现场验算结果基本相同，该方法因为能够进一步计算出维修人员的工作误差问题，对于整个民航维修工作开展具有影响。因此相关人员需要深入了解贝叶斯估算的技术要点，争取为更好的控制误差奠定基础。

参考文献：

[1]史海芳，李聪，姬永刚.序约束下单向分类方差分析模型的Bayes变量选择[J].吉林大学学报（理学版），2021，59（05）：1093-1100.

[2]郭云东，孙有朝.基于FIS-CREAM方法的人为差错风险评估[J].海军航空工程学院学报，2020，35（04）：303-309.

作者简介：顾远阳;性别：男; 1983年 11月;上海;汉;本科;助理工程师;民航维修人为差错评估技术探究。