一种幅度量化误差补偿策略*

李万珅，张达凯，刘胤凯，李熙民，冯孝斌

(电磁散射重点实验室，北京100854)

0 引 言

工程上对天线低副瓣电平(Side Lobe Level，SLL)的要求越来越高，常通过对阵列天线各阵元进行幅度加权控制以实现低副瓣方向图。目前进行幅度加权控制应用较多的是数字衰减器，其优点是可以较为精准、快速地实现对各阵元激励幅度的控制，缺点是受衰减步进和量化位数的限制，只能提供有限个确定的离散幅度值，势必产生量化误差，抬升SLL，影响天线性能。

对幅度量化的讨论大多在设计阵列天线尤其是稀布阵时对量化台阶和加权宽度的求解上[1-4]，而对于借助数字衰减器实现幅度加权的阵列天线，其量化台阶随着衰减器选型的确定已经确定，且数量较多，加权宽度求解也演变成对理想加权系数的量化问题。降低量化误差最直接的办法就是通过缩小衰减步进、增加量化位数来提高数字衰减器的精度，但需付出提高成本的代价。在不改变数字衰减器精度的前提下，若采取全局搜素，虽可得到最优解，但由于每个加权系数存在两种量化结果，随着阵元数的增加，计算量成指数增长，效率较低。目前所查阅文献多以就近量化(四舍五入)[5]作为量化策略，并未进一步细究，对较优解会有所遗漏。因此,如何在现有条件下寻求合理的幅度量化策略值得研究。

1 阵列模型及问题引出

考虑沿x轴排列的N元线阵，阵元间距d，借助数字衰减器进行幅度激励控制，其xoy平面内理想阵因子方向图函数[6]可表示为

(1)

式中：In(n=1,2,…,N)为各阵元幅度激励系数；k=2π/λ为传播常数，λ为波长；φ为方位角。

对于衰减步进为R0的M位数字衰减器，可以提供2M个相对幅度，即各阵元的归一化相对激励幅值只能取{1,β,β2,…,β2M-1}集合中的数值，其中β=10-R0/20。

阵因子量化方向图函数可表示为

(2)

式中：[·]代表某种量化策略。

误差方向图函数为

(3)

式中：δn=In-[In](n=1,2,…,N)为量化误差。

定义增益损耗偏移量(单位dB)为量化方向图与理想方向图的增益偏移值，可表示为

(4)

由式(3)和式(4)可知，对低副瓣算法求解出的幅度激励系数进行幅度量化，其误差方向图函数、增益损耗偏移量与具体采取的量化策略直接相关。

2 仿真分析

2.1 常见的量化策略

假设In∈[an,bn](n=1,2,…,N)，[an,bn]为数字衰减器量化区间，常见的量化策略有舍尾量化(取所在量化区间的左端点值)、进位量化(取所在量化区间的右端点值)和就近量化(取数值接近的量化端点值)。

此外，二可能值法(Two Possible Values，TPV)，依概率取左右量化端点值，常用来解决电扫描中移相器移相量化误差造成指向精度下降的问题[7-11]，本质上属于统计理论[12]。可将其用在数字衰减器幅度量化误差补偿策略中，并在此基础上提出统计意义下增益保持的二可能值法(Two Possible Values of Gain Hold，GH_TPV)，即

(5)

可见，当p=1时，即为舍尾量化；当q=1时，即为进位量化。除这两种极端情况之外，某个阵元的幅度激励值采取进位量化还是舍尾量化是随机的，由此可得误差方向图函数的期望为

(6)

式中：Δn=bn-an为In所在量化区间的区间长度。

本文重点关注量化方向图的增益损耗和最大SLL，不需拘泥于其他细节，故令量化后增益损耗偏移量期望为零，即

(7)

得出判决概率

(8)

以一维等间距侧射阵为仿真对象，仿真参数如表1所示，其中(a)、(b)、(c)、(d)为图1和图2的子图。

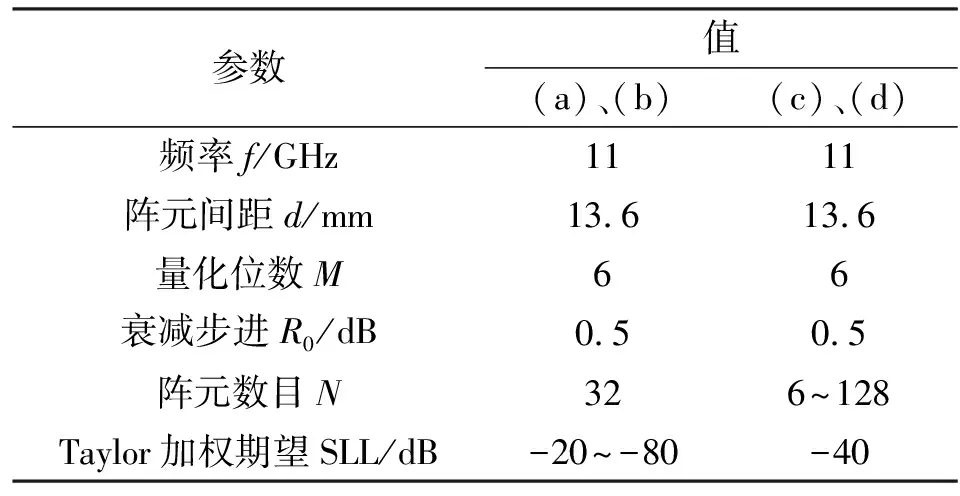
表1 一维仿真参数表

根据约束条件R0(2M-1)≥20lgK，得出数字衰减器可提供的幅度激励最大动态比K为37.58。采取Taylor加权[13]，随着期望SLL的降低，幅度加权的锥削度升高，K也不断变大。当期望SLL为-56.6 dB时，K为37.47。从图1(a)中也可以验证，当期望SLL小于-56.6 dB时，最大SLL的降低会受到衰减器精度(衰减步进和量化位数)的限制。

当期望SLL在-20～-40 dB之间时，进位量化和舍尾量化作为量化策略的两种极端，由式(4)可知其增益损耗偏移量较大。图1也表明，进位量化增益损耗降低，但最大SLL较高；舍尾量化最大SLL较低，但增益损耗增大。就近量化的增益损耗偏移量在±0.1 dB之内，但其最大SLL并非总是最优。图1中GH_TPV是在100次量化搜索中选取最优SLL的结果，由于当In数值接近an(或bn)时有q(或p)的概率置为bn(或an)，这将产生较大的量化误差，想得到较优结果，需大幅提高搜索次数，这将与全局搜索无异。而本文理想的量化策略应是在较少搜索次数下得到具有小增益损耗偏移量的同时，最大SLL又尽可能低，从而最大限度降低幅度量化带来的影响，故需要进行改进。

(a)N=32，最大SLL随期望SLL变化曲线

(b)N=32，增益衰减偏移量随期望SLL变化曲线

(c)-40 dB泰勒加权，最大SLL随阵元数目变化曲线

(d)-40 dB泰勒加权，增益衰减偏移量随阵元数目变化曲线

2.2 增益保持的适当二可能值法

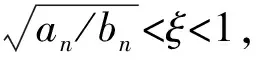
(9)

同样令E[ΔG]=0，得决策概率

(10)

式中：

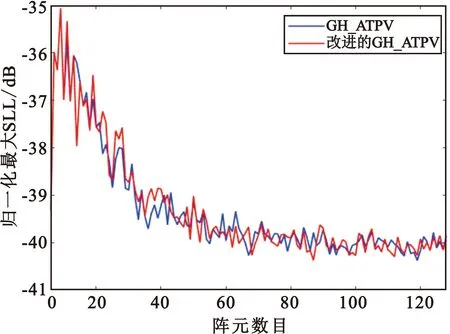
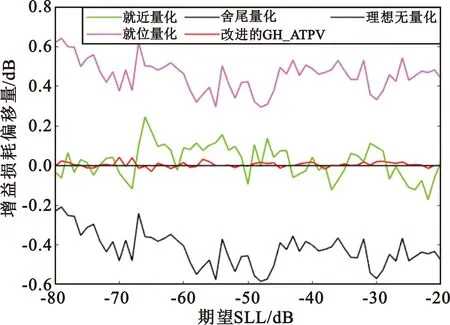
A={x|x=arg{an≤In≤an/ξ},n=1,2,…,N},
B={x|x=arg{ξbn≤In≤bn},n=1,2,…,N},
C={x|x=arg{an/ξ

(11)

GH_ATPV量化策略步骤如下：

Step1 设置量化搜素次数初值k=1，最大量化搜素次数为kmax，阈值系数ξ，最佳归一化量化副瓣电平初值SLL=0，最大副瓣电平初值SLLmax=0，最佳幅度量化加权系数Ibest。

Step2 由幅度加权系数得到其对应的量化区间，即In∈[an,bn](n=1,2,…,N)，并判断In在区间中所处的位置，得到集合A、B、C，由式(10)计算决策概率p。

Step3 根据式(9)对In进行量化，得到[In]GH_ATPV。

Step4 计算归一化量化副瓣电平SLL(k)，若SLL(k)

Step5k=k+1，若k>kmax，则停止搜索，输出Ibest、SLLmax；否则，转向Step3。

以Taylor加权为例，设kmax=100，ξ=0.985，仿真结果如图1所示。可以看出GH_ATPV增益损耗偏移量与就近量化相当，比同等搜索次数下的GH_TPV要小，其最大SLL优于四种常见的量化策略，量化效果较好且具有一定的普适性。对给定幅度加权值进行量化时，适当调整量化阈值系数ξ，可在较少量化搜索次数下得到较优的量化结果。

2.3 改进的GH_ATPV

采用GH_ATPV对每个不确定量化幅度加权值进行量化时，都是假设每个加权值的量化过程是相互独立的，但实际算法是逐次量化，当某个加权值量化结果确定后，其所带来的量化误差就随之确定，式(10)就会发生变化，此时决策概率应当实时更新，以便在一定程度上降低随机数的影响。

对GH_ATPV量化过程中决策概率进行实时更新，提出改进的GH_ATPV量化策略，其进行一次搜索的步骤如下：

Step1 设置加权值序数初值i=1。

Step2 由式(10)计算决策概率p(i)，按下述方法对Ii进行量化并更新集合A、B、C：

若i∈A，则[Ii]=ai；若i∈B，则[Ii]=bi；若i∈C，且rand(i)≤p(i)，则[Ii]=ai，A=A∪{i}，C=C-{i};否则[Ii]=bi，B=B∪{i}，C=C-{i}，其中rand(i)为0～1的随机数。

Step3i=i+1，若i>N，则完成本次量化；否则，转向Step 2。

以Taylor加权为例，设kmax=100，ξ=0.985，仿真得到改进前后的对比结果如图2所示。可以看出改进的GH_ATPV在保持与GH_ATPV相当的SLL水平基础上，增益损耗偏移量得到了进一步降低，且随着阵元数目N的增大效果更加明显。

(a)N=32，最大SLL随期望SLL变化曲线

(b)N=32，增益衰减偏移量随期望SLL变化曲线

(c)-40 dB泰勒加权，最大SLL随阵元数目变化曲线

(d)-40 dB泰勒加权，增益衰减偏移量随阵元数目变化曲线图2 改进的GH_ATPV与GH_ATPV对比

表2给出了以N=32为例、对部分期望SLL的Taylor加权系数进行1 000次kmax=50、ξ=0.985的量化仿真数据取平均的结果，进一步表明改进的GH_ATPV通过采取实时更新决策概率，充分利用已量化的数据信息，可保证其SLL与在GH_ATPV基本相当的前提下有着更小的增益损耗偏移量。

表2 改进的GH_ATPV与GH_ATPV相关数据

若C中最大的元素为j，则改进的GH_ATPV最终增益损耗偏移量的期望和方差只与p(j)和Ij有关，即E～(Ij-bj)+p(j)Δj，D～p(j)(1-p(j))Δj2，而GH_ATPV和GH_TPV一样，如式(11)，其增益损耗偏移量的期望和方差是多个独立随机变量期望和方差积累的结果。对图2中(a)、(b)量化搜索过程数据进行处理得到样本均值和方差，如图3所示，可以验证改进的GH_ATPV其增益损耗偏移量样本均值和方差优于GH_ATPV。

(a)平均增益损耗偏移量绝对值随期望SLL变化曲线

(b)增益损耗偏移量方差随期望SLL变化曲线图3 改进的GH_ATPV与GH_ATPV仿真数据处理结果对比

2.4 本文量化策略的二维推广

将本文提出的改进的GH_ATPV量化策略推广到二维阵列，关注二维阵列在两垂直面(φ=0°，φ=90°)上的方向图。对可分离型二维阵列进行两维加权系数的量化，其本质与一维阵列一样。以32×32二维阵列为例，在φ=0°、φ=90°面上均采用Taylor加权，仿真参数见表3，仿真结果如图4所示。可以看出，本文提出的量化策略具有较低的SLL，且有较优的增益保持效果，即在可分离型二维阵列的量化上，本文提出的量化策略依然适用。

表3 二维仿真参数表

(a)φ=0°,最大SLL随期望SLL变化曲线

(b)φ=90°,最大SLL随期望SLL变化曲线

(c)增益衰减偏移量随期望SLL变化曲线图4 改进的GH_ATPV与常见的量化策略对比

3 结束语

本文仿真分析了几种常见的幅度量化策略对数字衰减器控制的一维等间距侧射阵幅度加权方向图副瓣电平、增益损耗的影响，在TPV的基础上提出了GH_ATPV量化误差补偿策略，并对其决策概率进行实时更新，提出了改进的GH_ATPV量化误差补偿策略。仿真结果表明，改进的GH_ATPV量化误差补偿策略在保持改进前SLL水平基础上具有较优的增益保持性能，最大限度地降低了量化误差对天线性能的影响，对一维低副瓣阵列天线的实现有一定的参考价值。在此基础上进行二维推广，仿真表明本文的量化策略对可分离型二维阵列加权系数的量化仍有较优的效果，但对更加复杂的二维阵列的量化策略还需进一步研究。