序贯三支决策阈值选取策略研究

王文琦，冯琴荣

山西师范大学数学与计算机科学学院，山西 临汾 041000

三支决策作为一种典型的粒计算方法，其研究可分为静态和动态两部分.根据三支决策的基本思路，如果信息不足或证据不足，就会推迟决策，直到出现更多、更充分的信息可以用于进一步决策.因此，从本质上讲，三支决策是一种动态的决策.Yao[1]提出的序贯三支决策模型是动态三支决策的典型代表，该模型的关键是借助新加入的信息，逐步将难以决策的部分转化为接受或拒绝决策.近几年，序贯三支决策作为一种有效、灵活的工具，受到了学者们的广泛关注[2～6].

在经典粗糙集及其扩展模型中，许多学者用一对上、下近似来表示对象集，但是，下近似缩小了对象集的研究范围，上近似扩大了对象集的研究范围.为了更准确地描述对象集，张等人[7]提出利用模糊割集构造对象集的近似集，找到了一个相对较好的近似集R0.5(X)，并研究了它的一些性质.张等人[8]在文献[7]的基础上提出了一般近似Rλ(X)所满足的运算规则,找到了能够比上、下近似更好的描述X的λ成立的区间，称之为最优近似,并讨论了Rλ(X)作为X的最优近似所满足的条件.Janicki R等[9]研究了不同相似度指标下最优近似的计算,并给出了相对应的算法.李[10]给出了经典粗糙集模型下求最优近似的启发式算法.王[11]基于极大一致块，设计了一种不完备信息系统下求最优近似的算法.高[12]研究了最优近似的矩阵计算方法及其增量更新.

我们注意到序贯三支决策过程与求最优近似的过程之间有着很大的相似性，受此启发，本文研究了序贯三支决策阈值对的选取问题并给出了一些有效建议，使得在序贯三支决策过程中省掉大量不必要的计算，提高了序贯三支决策的效率.

1 预备知识

在本节中，我们简要回顾粗糙集，上、下近似等基本概念.

定义1[13](粗糙集) 给定一个信息系统S=(U,A,V,f)，∀B⊆A，∀X⊆U，RB是U上的等价关系，X关于RB的上、下近似集分别定义如下：

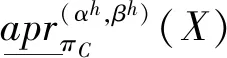
当αh>βh时，关于(αh,βh)的X的正域，负域，边界域为

在经典粗糙集及其扩展模型中，许多学者使用上、下近似两个精确的集合来描述目标集.最优近似是一个与目标集具有最大相似度的可定义集，相较于上、下近似，最优近似可以更好地描述目标概念.

(1)0≤S(A,B)≤1;

(2)S(A,B)=S(B,A);

(3)S(A,B)=1⟺A=B;S(A,B)=0⟺A∩B=∅,

则称S(A,B)是集合A和B的相似度.

定义4[8]给定一个信息系统S=(U,C,V,f)，对于任意的集合X⊆U,O(X)∈D(D是可定义集族)，如果O(X)满足以下条件：

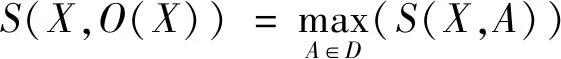
则称O(X)是X的最优近似.

2 序贯三支决策的阈值选取

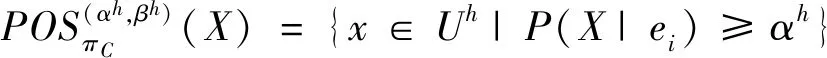
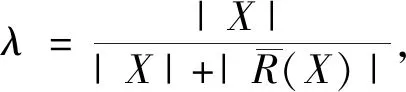
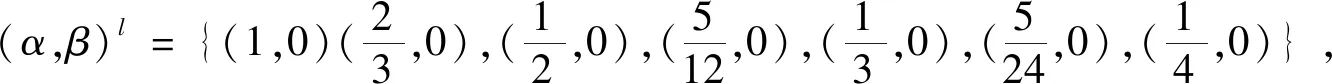
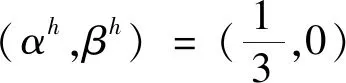
表1 正、负域随阈值对(αh,βh)的变化情况Tab.1 Change of positive and negative region with threshold pairs (αh,βh)

从例1中可以看到序贯三支决策中，最优近似等于该决策过程中某几个参数对(αh,βh)对应的正域.由最优近似的启发式算法可知最优近似是在下近似的基础上添加等价类，也就是说，αh只有变化到某个等价类的包含度时，该等价类才可以加入最优近似中，由此可得使正域与最优近似相同的这些αh值是介于等价类包含度之间的.进而通过大量例子，我们得到以下结论.

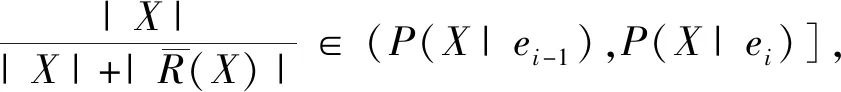
在序贯三支决策中，边界域中的一些等价类在阈值变化的过程中会逐步添加到负域中去，而且对象集的负域相当于对象集补集的正域.所以，我们可以把研究序贯三支决策中变化的负域等价为研究对象集补集的正域.

由以上分析可知,随着αh,βh的变化，序贯三支决策正、负域可能不会变化，而且在Li[15]中，已经发现当a,b∈(ri-1,ri]，POSa(Y)=POSb(Y)，但文献中并没有给出如何确定ri-1和ri的值.结合最优近似的启发式算法，我们发现ri-1，ri的值可以取为等价类的包含度.接下来我们用例子来具体说明.

例2 (续例1)在序贯三支决策中，针对不同的阈值对(αh,βh)，相应的正、负域是如何变化的.

表2 正、负域随阈值对(αh,βh)的变化情况Tab.2 Change of positive and negative region with threshold pairs (αh,βh)

从表2中可以看出，当我们对等价类的包含度按数值大小排序后，相邻大小的两个包含度构成一个区间，处在同一区间的αh、βh分别对应的正、负域是相同的，而且它们的并集就是论域.

命题3 给定信息系统S=(U,C,V,f)及一个动态阈值序列(α,β)l={(α1,β1),(α2,β2),...,(αl,βl)},αh≥βh(h=1,2,...,l)在序贯三支决策中，X⊆U,U/C={e1,e2,...,em},X相对于等价类ei(i=1,2,...,m)的包含度为P(X|ei)，不妨假设，P(X|e1)

(1)∀(αp,βp),(αq,βq)∈(α,β)l,若αp、αq∈(P(X|ei-1),P(X|ei)],则POS(αp、βp)(X)=POS(αq、βq)(X).

(2)∀(αp,βp),(αq,βq)∈(α,β)l,若βp,βq∈[P(X|ei-1),P(X|ei)),则NEG(αp、βp)(X)=NEG(αq、βq)(X).

命题4 给定信息系统S=(U,C,V,f)及一个动态阈值序列(α,β)l={(α1,β1),(α2,β2),...,(αl,β)},αh≥βh(h=1,2,...,l)在序贯三支决策中，X⊆U,U/C={e1,e2,...,em},X相对于等价类ei(i=1,2,...,m)的包含度为P(X|ei)，不妨假设，P(X|e1)

在序贯三支决策中，阈值参数αh,βh∈[0,1]，αh,βh可以组成无限多个阈值对，我们研究发现阈值参数可以区间化，而且每个区间的端点值可以取为等价类的包含度.这样就可以把无限多可能的阈值对离散化为有限多个阈值参数区间，从而对应有限多个正域和负域.这一发现对序贯三支决策阈值对的选取具有很大的指导意义.因此，通过计算等价类的包含度来选取αh,βh的值，可以大大减少不必要的计算.

我们将序贯三支决策中不同的阈值区间与不同正、负域的对应关系总结如下.

命题5 给定信息系统S=(U,C,V,f)及动态阈值序列(α,β)l={(α1,β1),(α2,β2),...,(αl,βl)},αh≥βh(h=1,2,...,l)在序贯三支决策中，X⊆U,U/C={e1,e2,...,em},X相对于等价类ei(i=1,2,...,m)的包含度为P(X|ei)，不妨假设，P(X|e1)

命题6 给定信息系统S=(U,C,V,f)及动态阈值序列(α,β)l={(α1,β1),(α2,β2),...,(αl,βl)},αh≥βh(h=1,2,...,l)在序贯三支决策中，X⊆U,U/C={e1,e2,...,em},X相对于等价类ei(i=1,2,...,m)的包含度为P(X|ei)，不妨假设，P(X|e1)

在序贯三支决策过程中，随着参数的变化，目的是缩小边界域，扩大正域和负域.因此，当我们选择阈值对(αh,βh)时，可以在等价类的包含度构造的区间中任选一个值，这样可以大大减少运算量，提高序贯三支决策的效率.

3 结论与建议

本文主要研究了序贯三支决策阈值对的选取问题.我们首先发现了序贯三支决策过程和寻找最优近似的过程很类似，并进一步发现了序贯三支决策的阈值参数可以进行区间化，在同一区间中选择不同的阈值参数得到的决策结果是相同的.因此，本文的主要工作是把序贯三支决策中阈值对的无限多可能取值减少为有限个可能取值，这对序贯三支决策的理论和应用都有重要意义.