一类二阶变系数非齐次线性微分方程的通解

邓瑞娟，崔洪瑞

1.芜湖职业技术学院基础部，安徽 芜湖 241003；2.广东药科大学医药商学院，广东 广州 510006

0 引言

线性微分方程是微分方程的重要组成部分，在生产实际中应用极其广泛.因此，如何寻找线性微分方程的通解，成为求解很多数学模型的关键步骤.自微积分创立以来，对线性微分方程通解的研究几乎就没有停止过，也得到了很多有意义的结论，但大多数的研究主要是围绕常系数情形展开的[1～3].

除了常系数的情形之外，变系数线性微分方程在动力学、工程学、经济学中也是很常见的.其通解虽不易求，但也有一些结论出现[4,5].其中，文献[4]讨论了形如

y″+p(x)y′+q(x)y=0

(1)

的二阶变系数齐次线性微分方程.文中指出

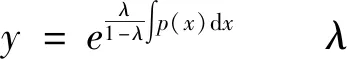
为(1)式特解的充要条件为

(2)

成立.同时，(1)式通解可表达为

(3)

其中C1、C2为任意常数.但是文献[4]中对于非齐次的情形未予讨论.

本文旨在文献[4]的基础之上，运用常数变易法给出非齐次情形下微分方程的通解，并将结果推广至二阶欧拉方程.

1 二阶变系数非齐次线性微分方程的通解

二阶变系数非齐次线性微分方程形如

y″+p(x)y′+q(x)y=f(x)

(4)

其中p(x)、q(x)、f(x)为连续函数，其对应的齐次方程即为(1)式.

运用高阶常数变易法[6]，令

(5)

y1和y2是方程(1)的基本解组，因此，Y(x)=c1y1+c2y2为齐次方程(1)的通解.现只需确定未知函数v1，v2，使(5)式满足非齐次方程(4)，即可得到对应的非齐次情形的通解.将(5)式代入原方程，可得v1，v2满足如下方程组.

因此，非齐次方程(4)的通解可总结为下述定理.

定理1 若存在常数λ(λ≠0,1)，使得方程(4)的系数p(x)、q(x)满足(2)式，则方程(4)的通解可表示为

(6)

其中

当W=y1y2′-y2y1′≠0时，

为上述方程所对应的齐次方程的两个特解，而

代入(6)式可得方程通解

其中C1、C2为任意常数.

2 二阶欧拉方程的通解

欧拉方程是描述流体运动的最重要的方程之一，由著名数学家欧拉首先提出，后广泛应用于动力学、弹性力学、热传导、金融投资等众多领域[7～10].因为是变系数线性微分方程，求解较为困难.本文将定理1运用于二阶欧拉方程，得出当欧拉方程的系数满足一定条件时的求解公式.

推论1 对于二阶欧拉方程x2y″+axy′+by=g(x)(a≠0，g(x)为连续函数)，若存在不为0或1的常数λ，使得

(a+b)λ2+(a2-2b-a)λ+b=0

(7)

则方程的通解为

(8)

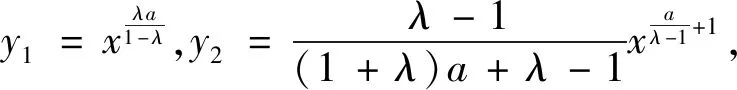
证明 对二阶欧拉方程两边同时除以x2，可将欧拉方程转换为方程(4)的形式

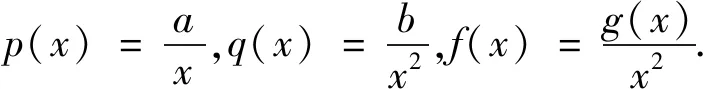
(a+b)λ2+(a2-2b-a)λ+b=0

当λ≠0,1时，运用定理1，可知方程有形如(6)式的通解，将p(x)、f(x)代入，可得

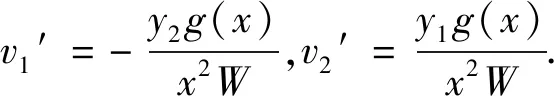
当a=0时，可验证必有λ=1，因此需排除此情况.证毕.

特别地，当b=0，a≠0,1时，可求得λ=1-a.于是，可得如下推论2.

推论2 对于二阶欧拉方程x2y″+axy′=g(x)(a≠0,1，g(x)为连续函数)，则方程通解为

其中

例2 求方程x2y″+2xy′-12y=7x4方程的通解.

解 将a=2,b=-12代入(7)中，有-10λ2+26λ-12=0.取λ=2，于是

可得

W=x-2≠0v1′=-x7v2′=7

于是，上述方程的通解为

例3 求方程x2y″-2xy′=x4-2x2的通解.

解 由推论2可知，b=0，a=-2，则

得通解为

例3也可通过设u=y′，用降阶方法求解.但是运用推论2的结论更为简单便捷.

3 结语

变系数非齐次微分方程应用广泛，但结果难求.通过运用常数变易法，将文献[4]中的结果推广至非线性情形，得出相应通解公式，完善了文献[4]中相关结论；欧拉方程一般的求解思路是使用变量代换，将其转化为常系数线性微分方程求解，本文则给出了另一种求解思路，运用定理1结论给出了相应的求解公式，该方法对系数限制较小，求解过程简单，适用范围广.