自适应稀疏模糊聚类模型

2021-11-01高云龙赖文馨潘金艳康丽雯

厦门大学学报（自然科学版） 2021年6期

高云龙，赖文馨，潘金艳，康丽雯

(1.厦门大学航空航天学院，福建厦门 361102；2.集美大学信息工程学院，福建厦门 361021)

模式识别是一种计算机和数学技术的结合，它通过对研究对象的分析研究，揭示其各因素之间存在的确定或是随机的规律，从而达到对研究对象描述、辨别、分类以及解释的目的.其技术方法主要分为监督模式识别与无监督模式识别.监督模式识别是指用一种已知类别样本作为训练集，建立分类器；而无监督模式识别是在未知划分类别与训练样本的情况下，对未知样本进行特征提取，进而进行聚类分析.无监督聚类分析算法的研究是模式识别领域的热门问题.

C均值是一种典型的无监督硬划分聚类算法，而基于C均值提出的模糊C均值(fuzzyC-means,FCM)聚类算法，虽然有效地解决了C均值聚类中心趋同的情况，但是由于模糊概念的引入，出现了新的问题.首先，FCM建模方法中存在同一样本点对各个聚类中心的隶属度之和为1的约束条件，这表明离群点及噪声的作用必然存在；在该条件的作用之下，聚类结果无法摆脱噪声和离群点对聚类质量的影响.其次，随着样本点同整体数据簇的偏差程度的增加，模糊隶属度具有拖尾和翘尾的特性，即本该被舍弃的异常点或离群点反而陷入了极度模糊的状态；这使得数据簇的类内聚程度降低，且混入了部分可分性特征，进而也降低了数据簇间的可分性.针对上述两个问题，大量基于FCM的模糊聚类算法被提出，主要围绕以下3个方面展开.

考虑对噪声和异常点的鲁棒性：FCM对噪声与异常点的高敏感特性，主要源于其同一样本点对各聚类中心的隶属度之和为1的约束条件的设置.于是Krishnapuram等[1]提出了PCM(possibilisticC-means)聚类模型，该模型将模糊聚类放在可能性理论的框架之下，考虑各个样本的“各异性”及其与各聚类中心的内在联系，使得噪声点和异常点对任意聚类中心的隶属度有可能被降到最低.然而由于PCM没有考虑数据簇之间的相互关系，其对初始参数的设置极其敏感，且易出现聚类中心趋同的情况，这显然违背了模糊隶属关系最初引入的意图.Pal等[2]提出了一种将FCM与PCM相结合的FPCM(fuzzy-possibilisticC-means)模型，该模型不仅具有FCM不同数据簇间相互作用的特性，而且具有PCM降低噪声异常值影响的优良特征，因此具有较高质量的聚类结果.但当样本量十分庞大时，由于FPCM全体样本点对同一聚类中心可能性之和为1的条件设置，每个样本点的作用将微乎其微，使得模型迭代难以收敛.为了解决这个问题，Pal等[3]又提出了PFCM(possibilistic-fuzzyC-means)模型，该模型的改进之处在于进一步明确了聚类数据簇的模糊模型，均衡考虑了各样本点的隶属度以及可能性，放松了可能性之和约束为1的条件.但同时该模型引入了需要用户设置的超参数，使得模型变得复杂且不具有自适应特征.

考虑数据簇的内聚程度与可分性：FCM过多地考虑数据簇内聚程度，而将部分判别信息纳入其中，反而使得类内聚程度下降，簇间可分性降低，具体表现为可见FCM的翘尾特性.例如在数据集中存在着一些离群点，而在不去除该异常样本点的情况下，按照距离划分的策略，应该将其归属于较近的一类数据簇.然而FCM作用下的离群样本的隶属度会陷入“极端模糊状态”，这使得两类数据簇的内聚程度以及可分性下降.因此对于该类离群值的挖掘至关重要，有效地判别离群样本，考虑样本间的“各异性”，可以获得更高质量的聚类结果.

部分学者在该角度上对聚类算法进行了研究，提出了将局部领域空间信息引入聚类模型的新想法.这类算法可减少离群点对聚类结果的负面影响,提高诸如图像处理的质量.例如：Ozdemir等[4]提出ICS(inter-cluster separation)模型，在FCM的目标函数中添加由聚类数据簇中心所确定的类间可分性；Veenman等[5]在两个相邻数据簇相互配合的基础上，对数据簇方差进行硬约束，从而使聚类结果的划分更加清晰；Cheng等[6]通过统计不同数据簇聚类中心的希尔伯特-施密特独立性来描述不同数据簇之间的可分性.受到簇间可分性研究的启发，Deng等[7]和Forghani[8]将类间可分性信息引入到模糊软子空间聚类模型中；Wu等[9]在PCM的基础上引入类间可分性，以避免不同的数据簇聚类中心趋于一致.

随着最小绝对值收敛和选择算子(least absolute shrinkage and selection operator，LASSO)、套索算法和正则化技术的发展和广泛应用，众多学者把正则化技术引入到FCM中，通过对模糊隶属度的正则化约束提高FCM对噪声和异常样本点的鲁棒性.例如：Xenaki等[10]在PCM框架下对隶属度进行了稀疏性处理，提出了稀疏正则化的可能性聚类方法SPCM(saprse PCM)，通过对隶属度矩阵施加稀疏性，从而有效剔除了噪声和异常样本点的影响.Zarinbal等[11]在FCM框架下提出REFCM(relative entropy FCM)，采用相对熵正则化技术，降低噪声和异常样本点的影响.Zhu等[12]提出了一种改进的模糊划分广义FCM聚类方法GIFP-FCM(generalized FCM clustering algorithm with improved fuzzy partitions)，该方法能够较好地分割带纹理的噪声图像.Zhang等[13]基于松弛法，提出了偏差-稀疏FCM(deviation-sparse FCM,DSFCM)，通过对偏差施加稀疏性,DSFCM对噪声和异常样本体现出较好的识别和处理能力.

本文结合以上3个方面的想法，提出了一种新的聚类算法，利用正则化技术与软阈值方法获得稀疏性结构特征，以此提高模型对噪声的鲁棒性，同时引入了虚拟类，挖掘离群点，把握数据样本的“各异性”，从而获取更高质量的聚类结果.

1 相关工作

1.1 FCM聚类

FCM算法的标准化目标函数与其约束条件如下所示：

(1)

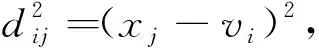
按照FCM的算法思想，其算法步骤可归纳如下：

对于给定的样本数据集X、数据簇个数c、最大误差阈值ε、最大迭代次数n，返回隶属度矩阵U以及聚类中心矩阵V.

1) 初始化隶属度矩阵U(0)以及聚类中心V(0)，迭代次数为t=1.

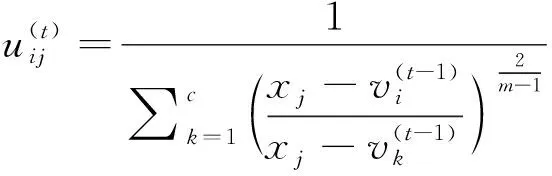
4) 当‖U(t+1)-U(t)‖<ε或者达到迭代最大次数停止，输出隶属度矩阵U和聚类中心矩阵V；否则返回第2)步，迭代次数t=t+1继续迭代.

由于FCM存在硬性约束条件，即同一样本点对各聚类中心的隶属度之和为1，FCM对噪声与离群点特别敏感，容易在该部分陷入极度“模糊”的状态.其过于关注样本点的内在联系，而忽略了样本的“各异性”，对噪声的鲁棒性较差，尤其不适合进行离群值的挖掘，容易得到质量较低的聚类结果.除此之外，FCM还存在着极易陷入局部最优解的缺陷以及倾向于均分数据簇的问题.

1.2 PCM聚类

PCM的标准化目标函数及约束条件如下所示：

(2)

其中λi为惩罚系数.通过分析可知，PCM在FCM的基础上，引入了松弛项，放松了对隶属度之和为1的约束条件，以达到改善FCM存在的对噪声以及离群点敏感的问题.

根据PCM算法的思想机制，其算法步骤可归纳如下：

对于给定的样本数据集X、数据簇个数c、最大误差阈值ε、最大迭代次数n，返回隶属度矩阵U以及聚类中心矩阵V.

将FCM返回的隶属度矩阵U以及聚类中心V作为初始化结果，并且以此计算惩罚因子作为初始值，迭代次数为t=1.

4) 当‖U(t+1)-U(t)‖<ε或者达到迭代最大次数停止，输出隶属度矩阵U和聚类中心矩阵V；否则返回第1)步，迭代次数t=t+1继续迭代.

PCM虽然解决了FCM的部分缺陷问题，但由于其模型的构建方式，PCM同样存在问题.从隶属度迭代公式中可以观察到：当惩罚因子很大时，隶属度uij将会趋近于1；当惩罚因子很小时，隶属度uij将会趋近于0.这正是PCM能有效地改善噪声问题的关键所在.但这同样表明模型具有特别高的灵敏度，非常依赖参数的设置以及聚类中心的初始化，使得迭代过程非常容易陷入聚类中心重合的困境，而这显然是很不利于寻找最优解的.

1.3 PFCM聚类

PFCM是FCM与PCM的结合模型，其标准化目标函数及约束条件如下所示：

(3)

PFCM在FCM的基础上引入了概率权重tij，同时参照PCM的做法，对tij的约束进行放松，这样能避免FPCM由于样本容量过大而导致的概率权重变得非常小时产生的计算误差.

根据PFCM的算法思想机制，其算法计算步骤可归纳如下：

对于给定的样本数据集X、数据簇个数c、最大误差阈值ε、最大迭代次数n，设定参数a和b，将FCM返回的隶属度矩阵U以及聚类中心V作为初始化结果，取概率权重矩阵T等于隶属度矩阵U为初始值，并且计算惩罚因子，此时迭代次数为t=1.

5) 当‖U(t+1)-U(t)‖<ε或者达到迭代最大次数停止，输出隶属度矩阵U和聚类中心矩阵V；否则返回第1)步，迭代次数t=t+1继续迭代.

虽然PFCM在一定程度上克服了FCM以及PCM所存在的问题缺陷，但是从其模型设置以及计算公式的推导中可见，该模型依赖于多个参数设置，不具有较强的自适应特性.

2 适应稀疏模糊(ASFCM)聚类模型

2.1 ASFCM

在此，本文提出一种新的模型：

(4)

上述模型中,β是权重系数，λj是第j个样本点隶属于虚拟数据簇的可能性权重，该权重的取值设置方式将在后文详细说明.其余符号的含义与FCM模型的相同.

由前文可知，FCM模型的提出虽大大改善了C均值的趋同性等缺陷，但又暴露出新的问题.其中，模糊概念的引入导致离群点陷入过于模糊的状态，即隶属度呈现翘尾状态，这一问题亟待解决；同时其隶属度之和为1的约束，使得算法对噪声和离群值更加敏感.

针对上述两大问题，本文在FCM模型的基础上，再次引入C均值模型来达到有效抑制FCM的翘尾特性的目的.除此之外，模型(4)中引入了一个虚拟的噪声数据簇，算法会将自动判别出的噪声划分到该虚拟数据簇中，以此挖掘离群值的信息，并降低离群点对聚类结果的影响.

综合来看，模型的后两项作为正则化项，使得模型具有稀疏结构特征.

ASFCM没有把所有数据样本放在同等地位，不会因为过于关注所有数据的内在联系而忽略了样本的差异，其将样本划分成有效样本以及噪声样本两大部分，即能够很好地把握样本数据的“各异性”.

2.2 隶属度取值稀疏性

参考Zhang等[14]获取具有稀疏特征的相似度矩阵的优化步骤，可以利用拉格朗日乘子法进行求解，并获得如下表达式：

(5)

其中η,γ≥0,均为拉格朗日乘子.根据KKT(Karush-Kuhn-Tucker)条件，可以获得如下信息：

(6)

这里采用软阈值方法进一步分情况讨论，可得：

(7)

根据上述情况综合讨论可得:

(8)

式(8)表明，该隶属度取值符合软阈值方法特征，具有稀疏特性.同时容易看出，隶属度取值的稀疏性可以有效地挖掘出离群点信息，将离群点划分至引入的虚拟噪声数据簇，从而有效地排除此类异常值对聚类结果的影响，能够在一定程度上提高数据簇的类内聚程度以及数据簇之间的判别特性.

2.3 模型求解分析

为了便于模型的求解，对式(8)中λj进行设置：λj=δ-η，其中δ为可设置的参数，称δ为鲁棒距离阈值.于是进一步获得隶属度的表达式如下：

(9)

对于被引入的虚拟噪声数据簇，取值为

(10)

由隶属度表达式可看出，δ的取值小于样本点到任一聚类中心距离时，虚拟数据簇的隶属度恒为1.选取合适的鲁棒距离阈值，可以极大程度排除噪声的影响，这表示ASFCM对噪声具有较好的鲁棒性.在合理设置鲁棒距离阈值的基础上，ASFCM所获得的隶属度可根据实际实验数据的分布特点，以及其具体样本与聚类中心的距离进行自主调整，自动且高效地判别噪声.基于这一性能表现，该算法具有自适应特性.

为了获取聚类中心的迭代公式，再次利用拉格朗日乘子法进行求解.对式(5)中的vi进行求导后整理可得：

(11)

进一步整理可以得到聚类中心的表达公式：

(12)

根据上述模型求解结果，可归纳ASFCM的算法流程如下：

对于给定的样本数据集X、数据簇个数c、最大误差阈值ε、最大迭代次数n，设定可调参数δ，返回隶属度矩阵U以及聚类中心矩阵V.

1) 初始化隶属度矩阵U(0)以及聚类中心V(0)，迭代次数为t=1.

2) 根据式(9)对uij，根据式(10)对u(c+1)j进行迭代更新.

3) 根据公式(12)对进行迭vi代更新.

4) 当‖U(t+1)-U(t)‖<ε或者达到迭代最大次数停止，输出隶属度矩阵U、聚类中心矩阵V；否则返回第2)步，迭代次数t=t+1继续迭代.

接下来进行对比实验验证ASFCM的性能.

3 实验部分

在接下来的实验中，鲁棒阈值距离的参数设置将根据具体实验数据的离散程度(如方差)进行初步设置，并根据效果进行参数微调.在合理的设置范围内，δ越大则去噪能力越弱，δ越小则噪声能力越强.

3.1 隶属度曲线实验

正如前文所述，FCM对离群值极度敏感，这种特点的具体表现是，该算法无法排除离群值的影响，而离群值的隶属度会陷入过度模糊，进而导致错误划分的情况.

为了能够直观地展现FCM的翘尾特性，说明本文所提出的模型ASFCM能有效克服这种缺陷，在本实验中，随机生成了两个一维数据簇，并在数据簇周围叠加了10%的离群数据点，再存储为一维数组，有效样本数据与噪声数据共有22 000个.先将样本按大小进行排序后，分别利用FCM算法以及本文的新算法ASFCM计算隶属度，并将隶属度曲线绘制在图像上，结果如图1所示.图中的虚线是FCM计算下其中一个数据簇的隶属度曲线，该曲线在两端呈现趋向于0.5的状态，而在模糊的概念中，0.5的隶属度代表的是完全模糊，这显然不利于聚类的进行，即FCM存在的翘尾问题；而图中的实线是ASFCM聚类结果的同一数据簇的隶属度曲线，可以明显地看到，对于离群噪声数据，ASFCM能够完全排除其影响，即这类噪声对任意数据簇隶属度皆为0，这显然符合我们对聚类结果的理想预期.

图1 FCM与ASFCM的隶属度曲线对比Fig.1 Membership curve comparison of FCM and ASFCM algorithms

图2所示为经过ASFCM的处理后，一个有效样本数据簇和引入的虚拟数据簇对所有样本点的隶属度曲线.可以看到，ASFCM可以自动判别出离群数据点，并将其划分至虚拟噪声数据簇中，也就是代表有效样本数据簇的虚线两端的截断，以及代表虚拟噪声数据簇的实线两端逼近于1.0的曲线走向.ASFCM通过有效样本及噪声的有效划分达到了降低离群值对聚类结果影响的目的.

图2 ASFCM对有效样本数据簇及虚拟噪声数据簇的划分结果Fig.2 Division results of ASFCM algorithm on data cluster and noise cluster

3.2 隶属度等高线图

为了能够进一步清晰地展示ASFCM对离群值的有效挖掘以及稀疏特性，本文中生成一组人造数据集，其由两个量级一致的数据簇以及叠加的部分离群噪声构成.

根据这组人造数据集，制作了FCM与ASFCM聚类结果的隶属度等高线分布图像(图3)，其等高线值取自样本对各实际数据簇的隶属度的最大值.

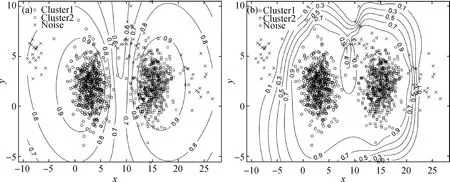
图3 FCM(a)和ASFCM(b)隶属度的等高线图Fig.3 The contour map of FCM (a) and ASFCM (b) membership degree

而ASFCM有着非常明显的稀疏结构特征，可以高效地去除离群噪声点的影响.对任意实际数据簇，ASFCM所计算出的噪声的隶属度都非常低(除了与有效数据重叠的噪声)，即几乎所有的噪声都被识别并被划分到引入的虚拟噪声数据簇中.这样的划分方式大大降低了离群值对聚类质量的影响，使得数据簇类内聚程度更高.

3.3 鲁棒性实验

本实验是利用两个等距离离群噪声来展示其对隶属度计算的影响(图4)，以此对比FCM、PCM、PFCM、GIFP-FCM、REPCM、ASFCM 6种算法对噪声的鲁棒特性(图5).

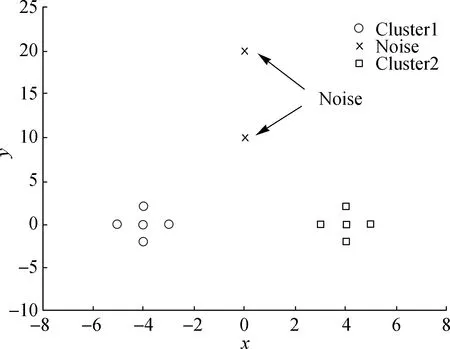
图4 两个有效样本数据簇和两个噪声Fig.4 Two data clusters and two noise samples

图5 6种算法的隶属度曲线Fig.5 Membership curves of six algorithms

分析图5可以得知，对于此类等距噪声，FCM虽正确地划分了样本标签，但两个噪声点的隶属度却是0.5，这表明隶属度中不存在任何判别信息，这两个噪声会被随机划分至任意数据簇中.而PCM与PFCM，虽都将两个噪声点的影响几乎降至0，但其隶属度曲线并非很完美，而且极度依赖初始参数的设置.GIFP-FCM虽然做到有效样本不模糊，即判别信息十分明确，但是它却完全无视噪声点的影响，直接将其划分至一类有效样本数据簇中，导致隶属度曲线的判别分界线出现明显的偏移.REFCM虽然在一定程度上降低了两个噪声的影响，但是极易出现聚类中心重合的情况，且曲线走势仍存在改进的空间.最后，我们的ASFCM计算出的结果，不仅把两个噪声点的影响完全排除，而且可将两个数据簇完全划分开来，可分性大大提高.

3.4 UCI数据集

UCI(University of California Irvine)数据集是一个常用的标准测试数据集，其来源于实际的生活生产中，具有分布形式多样、数据特征丰富的特点.本实验引入9个UCI数据集对算法的有效性进行验证，所使用的数据集特点如表1所示.

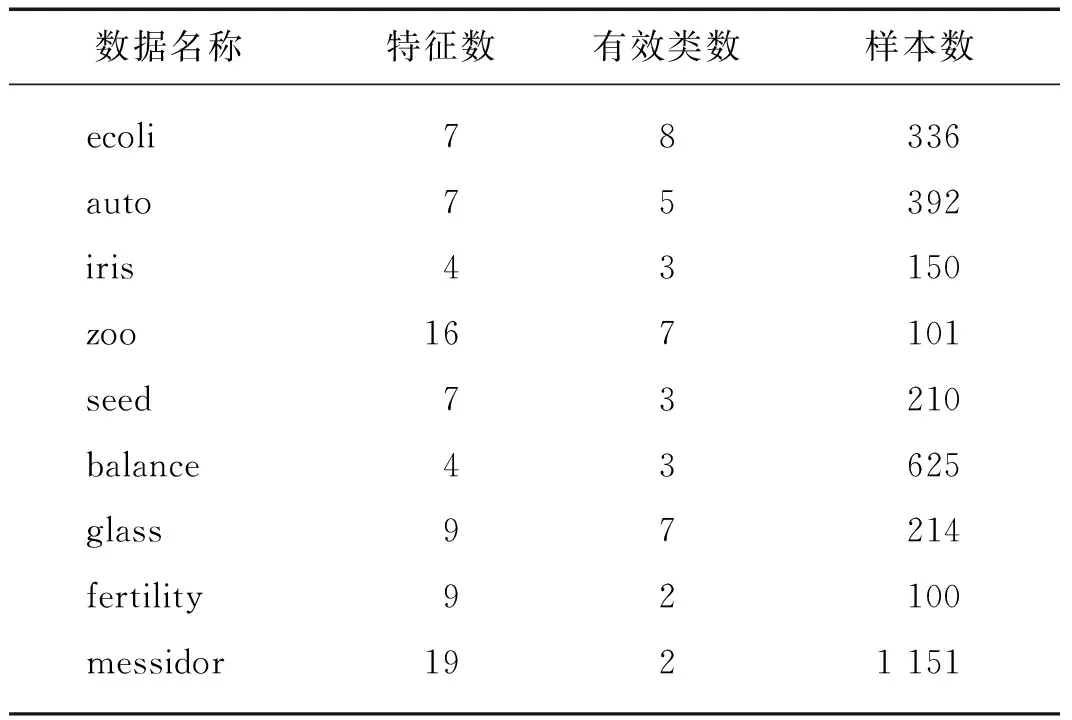
表1 UCI数据集特点Tab.1 The features of UCI datasets

为了评估不同的聚类算法，引入了兰德指数、标准化互信息及2种不同的聚类有效度评估方法，共4种指标进行实验对比评估.

首先，对4种指标进行简单介绍.

兰德指数RRI为常见的聚类评估指标，其表达式如下所示：

(13)

其中:f00表示实际类别信息一致并且聚类判别结果一致的样本个数，f11表示实际类别信息不同并且聚类判别结果不同的样本个数;N(N-1)/2表示样本内可组成的数据对个数;RRI的取值为0到1，RRI的值越大，表明聚类效果越好，类内纯度越高.

标准化互信息利用信息熵来衡量聚类结果，其表达式如下：

NNMI=

(14)

其中:Nij表示既属于集合i又属于集合j的样本数量;Ni表示属于集合i的样本数量;Nj表示属于集合j的样本数量;N表示全体样本个数.其取值为0～1，值越大表明聚类结果一致性越高，因而可以用来评价带有标签信息的数据集.

基于欧式距离度量的聚类有效度EEVA是由类间分离度SSPT与类内紧致度CCMP共同衡量所得.

(15)

(16)

(17)

其中：Ni表示属于第i个聚类中心的样本个数；其余符号同FCM的符号含义.EEVA的取值越大，表示类内越紧致，类间分离程度越高，聚类效果越好.

为了避免单一的有效度评估方式造成的误差，根据朴尚哲等[15]对模糊聚类算法评估指标的整理论述，选取基于隶属度的聚类有效度量指数进行进一步的评估，其由紧致度C与相似度S共同衡量，表达式如下：

(18)

(19)

(20)

其中，

(21)

Sij=min(uik,ujk),k=1,2,…,n.

(22)

符号含义同FCM的符号含义.该指标越小，表明类内聚程度越高，类间分离度越好，聚类质量越高.

本实验利用UCI数据集中的9组数据进行测试，对于每个数据、每个算法，进行10次重复实验，并取聚类结果的平均值进行记录比较，记录结果如表2所示.其中标黑的是本文算法数据以及结果最优的数据,既标有下划线又标黑的数据表示虽指标最优但聚类中心重合.

表3记录了各算法的聚类有效度EEVA与VCS的平均值.虽然FCM算法表现出最高的EEVA指标，但是该算法无法排除离群噪声点的影响，因此尽管其聚类有效度EEVA最高，实际上聚类效果却并非最佳.其余算法在一定程度上都排除了噪声点的影响，虽然它们的聚类有效度EEVA都有下降趋势，但是综合表2以及VCS来看，聚类质量有所提高，尤其是ASFCM，该算法在尽可能保证EEVA指标较高的情况下，同时也较大幅度地降低了VCS指标.

联合表2与表3的结果进行具体分析.PCM与GIFP-FCM的聚类效果依赖参数的设置，尽管聚类结果多次出现高指标的情况，但这两种算法都出现了聚类中心趋同问题，直观表现是表3中对应的聚类有效度EEVA大幅度下降与VCS明显增大.PFCM的聚类质量相对较高，但对于它的多个超参数，无从获得其设置方法，只能依靠经验调试.而REFCM的参数灵敏度过高，微小的偏差会导致整个聚类结果质量的迅速下降，平均聚类有效度偏低.

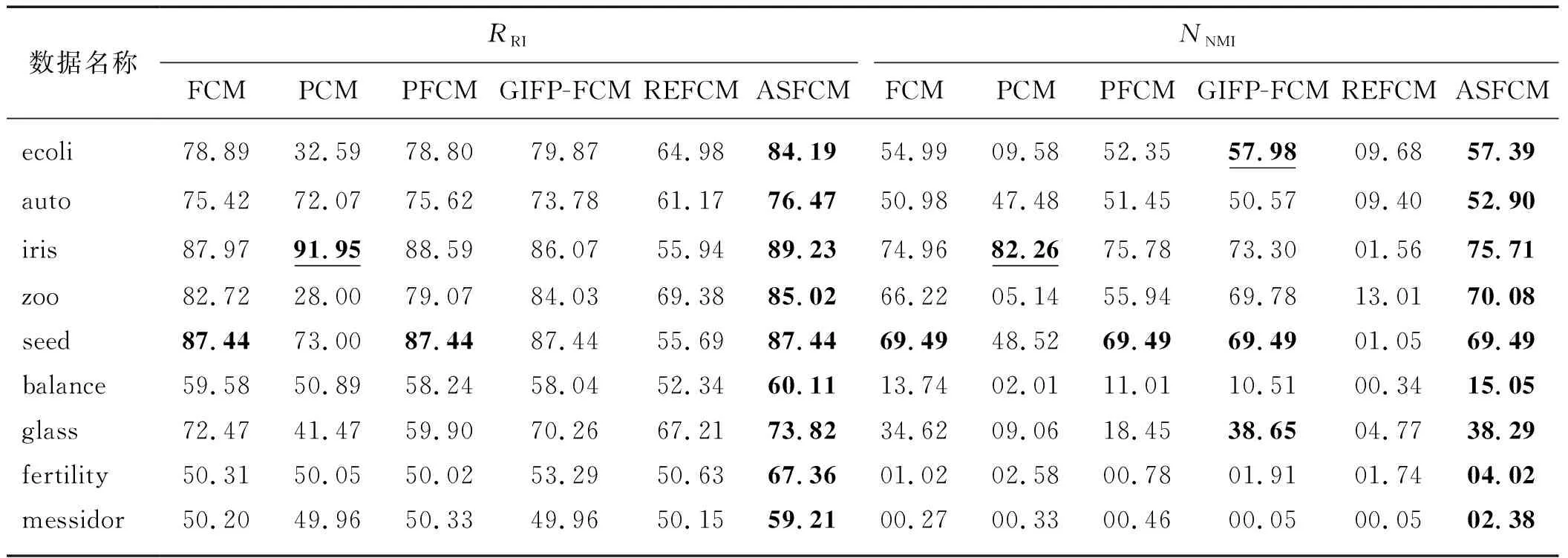
表2 UCI数据集实验结果Tab.2 Experimental results of UCI datasets %

表3 聚类有效度Tab.3 Validity indexes

可见利用UCI数据集的聚类分析所计算出的平均兰德指数、平均标准化互信息以及聚类有效度来评估，ASFCM整体优于FCM、PCM、PFCM、GIFP-FCM、REFCM 5种算法.

3.5 图像分割

在本实验中，分别利用FCM、PCM、PFCM、GIFP-FCM、REFCM以及ASFCM 6种算法进行图像分割，为了展现ASFCM算法对离群噪声的有效抑制，在每张彩色实验图片上叠加了椒盐噪声，并将算法自动判别出的划分至虚拟数据类的噪声点通过K最近邻(K-nearest neighbor,KNN)分类算法设置新的标签.具体实现方式为：计算以该像素点为中心的窗口内各相邻像素点标签的数量，取数量最大的标签作为该噪声点的标签，最后按照算法聚类出的新标签，同一数据簇中的样本点取均值还原图像.结果如图6所示，可以看出：无论是FCM、PCM、 PFCM、GIFP-FCM或REFCM都无法去除叠加的椒盐噪声的影响，但是ASFCM能够较大程度移除噪声信息，还原出较高质量的分割图像.ASFCM分割出的图像颜色区分度大，贴近原图色彩，这表示聚类结果中数据簇类内聚程度高，数据簇间可分性大.