横向过载对固体火箭发动机推进剂点火建压过程的影响

官典， 李世鹏， 刘筑， 王宁飞

(1.北京理工大学 宇航学院， 北京 100081； 2.中国运载火箭技术研究院 空间物理重点实验室， 北京 100076)

0 引言

固体火箭发动机是一种结构紧凑、性能优良的动力装置，其工作过程耦合了燃烧、传热、辐射、火焰传播、压力建立和凝聚相侵蚀等一系列复杂物理和化学现象[1]。有研究表明：在过载情况下(如旋转产生的径向过载或横向机动产生的横向过载)，发动机内的上述物理或化学过程均会发生较大改变，致使真实飞行中发动机性能与地面静止实验结果相差很大，甚至会因为地面设计的参考不当造成发动机殉爆事故[1-6]。对大部分飞行试验结果研究发现，发动机从初始点火到稳定燃烧过程极易出现故障。由于实验难度大和数值描述复杂等原因，目前学术界对过载下在推进剂点火建压过程中侵蚀燃烧与过载效应耦合规律的研究依然匮乏。为了预示这一规律并保证发动机大过载下正常开启和工作，对横向过载条件下推进剂点火建压期间燃烧性能变化规律进行研究是基础的且势在必行的。

针对无过载时固体火箭发动机点火演变规律，国内外学者通过实验与数值模拟等方法已经做了大量研究。各种测试手段(如压力传感器及其热电偶测试[7]、镭射多普勒速度场测试[8]以及高速摄影[9])能够准确地捕捉实验中的关键数据，反映部分实验现象。但由于固体火箭点火是强瞬态过程，工程上很难测量和记录丰富的瞬时数据。另一方面，数值仿真在研究多维下点火瞬态过程中已经逐渐得到成熟运用，如基于纯流体假设的数值模型[10-11]、基于两相流假设的数值模型[12-13]和流体- 固体耦合数值模型[14-15]，在数值结果与实验结果一致时，数值方法在研究发动机瞬态过程中具有特定优势。

截至目前，已经有很多学者开展了过载条件下推进剂燃烧性能的研究。Northam[16]发现作用在燃面上的加速度矢量角度和推进剂成分对燃速变化影响较大。Ye等[17]指出燃面附近雷诺数可用于描述微观燃烧模型中旋转和压力对气相火焰偏转角的影响。Caveny等[18]、Willoughby等[19]和Crowe[20]对过载情况下的推进剂燃烧规律都提出了半经验模型。Greatrix[21]、Greatrix等[22]、Greatrix[23]在前人基础上，引入燃面能量薄层和加速度质量通量系数，提出描述适用面更广的过载条件下推进剂燃烧特性的模型。关于推进剂的侵蚀燃烧，已经有很多学者建立了多种推进剂燃烧侵蚀模型。其中包括：Lenoir等[24]基于中心高温气流对流传热理论提出了L-R模型，该模型广泛应用于固体火箭发动机的设计中；Greatrix等[25]提出了优化型对流传热反馈模型，该模型对流动校正因子的依赖性较小；King[26]提出的火焰弯曲模型，从微观扩散火焰倾斜加大燃面热对流的方式解释了侵蚀效应。在此基础上，Guan等[27]采用数值模拟方法对高速自旋条件下小型发动机点火机理进行研究，得到了旋转过载下点火规律与无过载情况不一致的理论描述。

本文针对横向过载下推进剂点火建压特点，以静态点火建压模型为基础，将用户自定义函数(UDF)首次引入横向过载场模型、过载下推进剂燃烧模型以及侵蚀燃烧模型，对不同横向过载下发动机内推进剂点火建压规律进行研究。

1 物理模型和计算方法

1.1 发动机结构

为了检验侵蚀、传热和加质等模型在推进剂初始建压模拟中的正确性，参考Peretz静态点火实验[28]，建立与实验一致的物理模型，如图1所示。

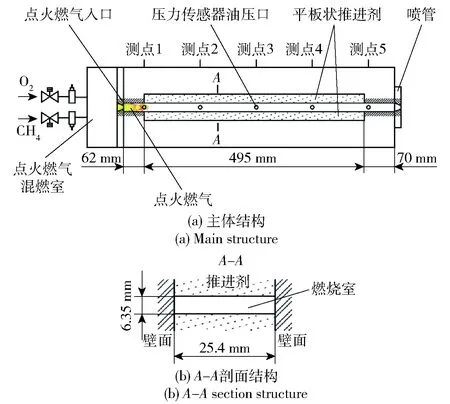
图1 内嵌双面推进剂的发动机结构示意图Fig.1 Structure diagram of rocket motor with two slices of propellant

在同一横向过载下，对称燃面因过载相对矢量角的不同而出现燃烧差异，为了达到控制单一变量的目的，在模型验证完后，将Peretz实验装置中双面推进剂装药形式改为单面推进剂装药形式，原有的另一面推进剂用等厚度钢材替代，如图2所示。下文所有物性和尺寸参数均与Peretz实验[28]统一。

图2 内嵌单面推进剂的发动机结构示意图Fig.2 Structure diagram of rocket motor with single slice of propellant

1.2 数值计算方法

发动机内流场使用基于k-ε双方程湍流模型的Navier-Stokes方程求解[29]。基于Fluent软件，使用UDF实现点火过程模拟。将过载场效应、侵蚀效应和过载燃速效应嵌入模型源项，表征横向过载下发动机内物理现象。发动机内流场区域控制方程包括如下质量、动量、能量守恒方程和状态方程：

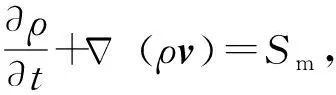
(1)

仅考虑燃气与推进剂表面之间对流传热。推进剂表面温度Ts作为点火判定依据，由(2)式和(3)式耦合计算获得。

(2)

式中：等号左项表示推进剂表面导热状态，右项表示对流换热量；λp为推进剂导热系数；Tp为推进剂温度分布函数；n为代表燃面法向。推进剂内二维瞬态传热方程如下：

(3)

式中：Cp为推进剂比热。

在本文中推进剂燃速rg主要受过载效应与侵蚀效应影响[21]，如(4)式所示：

rg=r0+Δre+Δrb，

(4)

式中：r0为推进剂基础燃速，r0=apn，a为燃速系数，n为燃速压力指数；Δre为因侵蚀效应带来的燃速增量，遵循L-R侵蚀燃速公式，参数依据文献[28]给出(见表1)：

表1 点火过程相关物性参数

Δre=ξ1hcexp(-βr0ρp/vrρr)，

(5)

(6)

ξ1和β为比例系数，hc为xr处推进剂表面对流换热系数，xr为距离装药前端的距离，vr为xr处气体流速，ρr为xr处气体密度，ξ2为比例系数，Pr为普朗特数，W为燃气摩尔质量，Tsg=(Ts+Tf)/2，dh为通道湿润周直径，Ap为xr处通道面积，At为喉部面积；Δrb为横向过载效应产生的燃速变化，由Greatrix等[22]和Greatrix[23]推进剂过载燃烧模型计算获得：

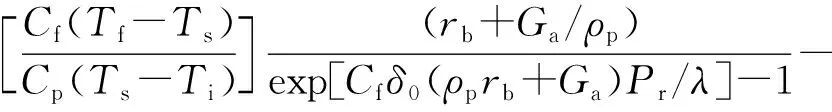
(7)

Ti为推进剂初温，λ为气相热导率，Ga为加速度的质量通量，如(8)式所示：

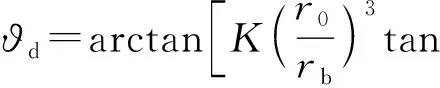
(8)

Ga0表示最大加速度质量通量，ϑd为增强定向角(即侧向/纵向位移角)，K为定向角修正因子，ϑ为加速度偏角，δ0为燃烧区厚度，如(9)式所示：

(9)

ΔHp为净放热量。

由于本文采用内嵌单面推进剂的发动机结构，控制了横向过载方向与推进剂表面矢量关系。图3列举了3种过载下过载场效应与过载质量通量Ga关系。图3(a)所示发动机不受加速度作用；图3(b)为推进剂所受加速度ay指出燃面，流场惯性加速a′y指入燃面(加速度a′y为正)，此时Ga=|Ga0|；图3(c)为当推进剂所受加速度ay指入燃面，流场惯性加速a′y指出燃面(加速度a′y为负)，此时Ga=0[30-31].后续提到的加速度均指惯性加速度a′y.

图3 过载场效应以及过载条件下的质量通量GaFig.3 Accelerative field effect and mass flux Ga in acceleration condition

依据(7)式、(8)式和(9)式，图4给出了推进剂过载燃速(rb=Δrb+r0)随过载和压力的非线性变化规律。由图4可见：当相对加速度指向燃面时a′y为正，燃速随过载和压力的增加而非线性增大；在加速度背离向燃面时a′y为负，燃速随过载幅值增加而略微减小，随着压力增加而非线性增加；相比负向加速度，正向加速度对燃速幅值变化的影响更大。

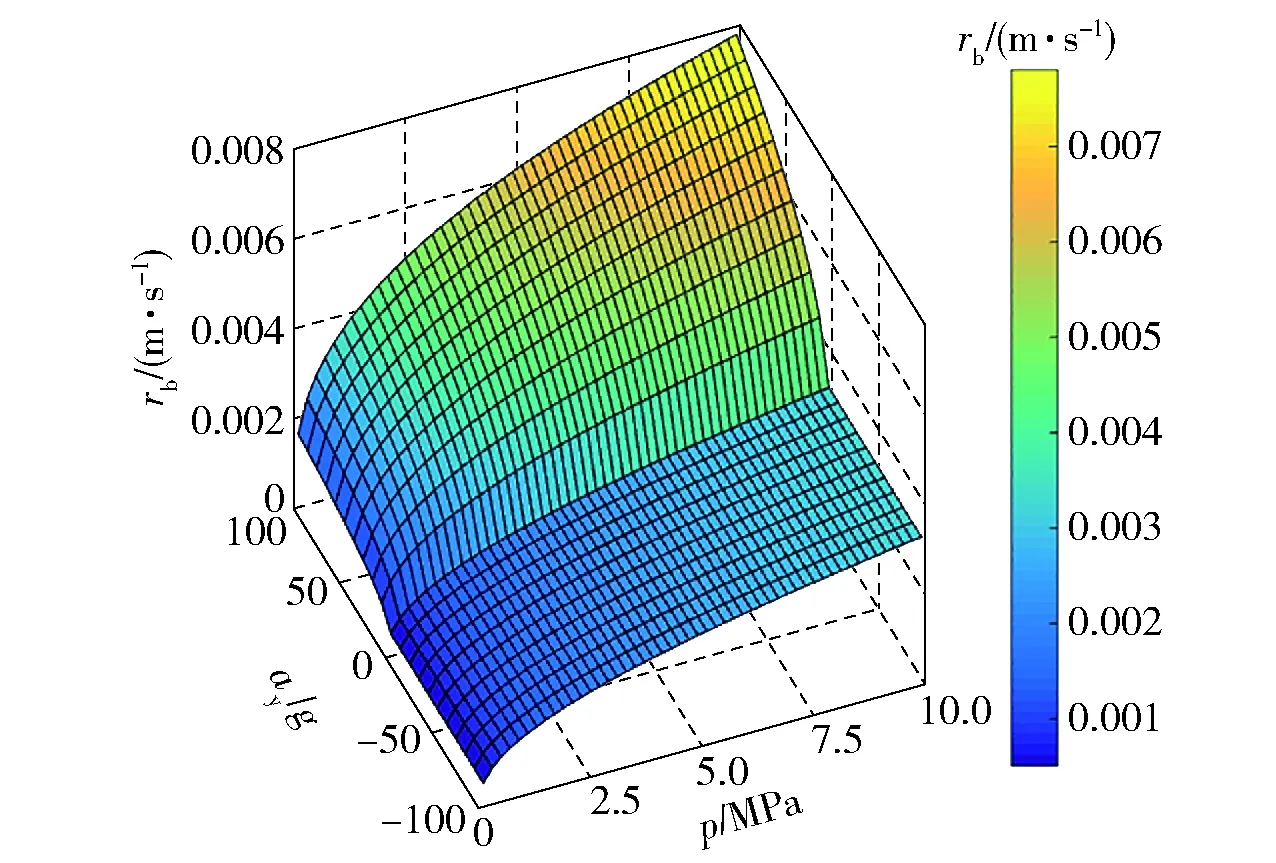
图4 推进剂燃速、表面过载与表面压力的非线性关系Fig.4 Non-linear relationship between propellant burning rate and surface acceleration and surface pressure

固体火箭发动机在点火时，腔体内气体高速流动，呈高雷诺数特征，并伴随有压缩波甚至冲击波。由于k-ε湍流模型适合完全湍流流动，采用k-ε对上述N-S模型进行封闭是适用的。湍流动能k及湍流能量耗散率ε分别由以下两式求得：

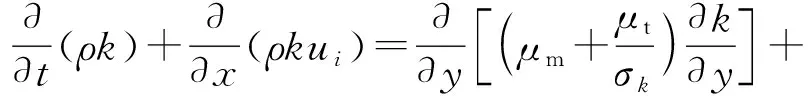
(10)

(11)

式中：ui为时均系数；μm为层流黏性系数；μt为湍流黏性系数，

(12)

表2 湍流模型中的常值参数[32]

本文点火模型的简化借鉴文献[28]，并加入过载相关假设如下：

1)基于发动机结构，将物理模型简化为二维平面模型。

2)使用固相点火准则作为点火判定条件，即壁面温度Ts大于点火温度视为燃面点燃；

3)不考虑化学反应，推进剂燃烧产物与点火器燃气具有相同的Cf、W和λ，均视为可压缩理想气体。

4)考虑燃气冲刷带来的侵蚀效应。

5)考虑过载情况下，流场受惯性力作用。

6)过载燃速效应基于Greatrix模型。

1.3 计算模型和边界条件

根据模型结构，本文建立Oxy平面二维数值模型(见图5)。图5中，沿着推进剂表面距离推进剂头部0.05L、0.50L和0.95L位置设置A、B和C点，L为推进剂长度，Coupled壁面固相网格第1层高度1×10-6m，Coupled壁面气相第1层网格高度5×10-5m. 由于气流流速变化较大，燃烧室两侧加密。点火入口采用质量流量入口，质量通量为93.18 kg/(m2·s)；出口采用压力出口；流体- 固体耦合交界面采用Coupled壁面，其他壁面采用绝热壁面，由于y+始终处于20～60之间，壁面函数采用标准壁面函数。初始温度298 K；初始压强101 325 Pa. 采用PISO算法对压力和速度进行解耦。密度、动量和能量等方程采用2阶迎风格式进行离散，瞬时项离散格式采用2阶隐格式。为了满足Courant-Friedrich-Levy(CFL)稳定条件，时间步长选取1×10-6s.

为了方便燃速研究，做如下定义：

Ab(i)=Δrb(i)/r0(i)，

(13)

式中：Ab(i)为推进剂表面A点在i时刻由过载效应带来的相对燃速增量，用以表示过载效应对推进剂燃烧的影响程度(Bb和Cb以此类推)；Ae(i)=Δre(i)/r0(i)，

(14)

式中：Ae(i)为推进剂表面A点在i时刻由侵蚀效应带来的相对燃速增量，表示侵蚀效应对推进剂的影响程度(Be和Ce以此类推)。

βj(i)=Δrj(i)/(Δre(i)+Δrb(i))，

(15)

式中：βj(i)为燃速增量占比，表示不同i时刻过载或侵蚀效应在燃烧变化过程所占比重；j=e或b，代表侵蚀作用或过载作用。

1.4 数值验证

数值仿真结果与Peretz的无过载固体火箭点火实验数据对比如图6所示。由图6(a)可见，数值计算得到的瞬变压力在点火滞后期和火焰传播期与静态数据十分贴近，峰值压力误差小于5%，表明该模型对瞬变压力的预测具有较高精度。图6(b)为不同时刻沿轴向压力分布，可以发现该模型对发动轴线压力分布预测准确性均较高。上述结果验证了本文所建传热、侵蚀和加质模型的合理性。

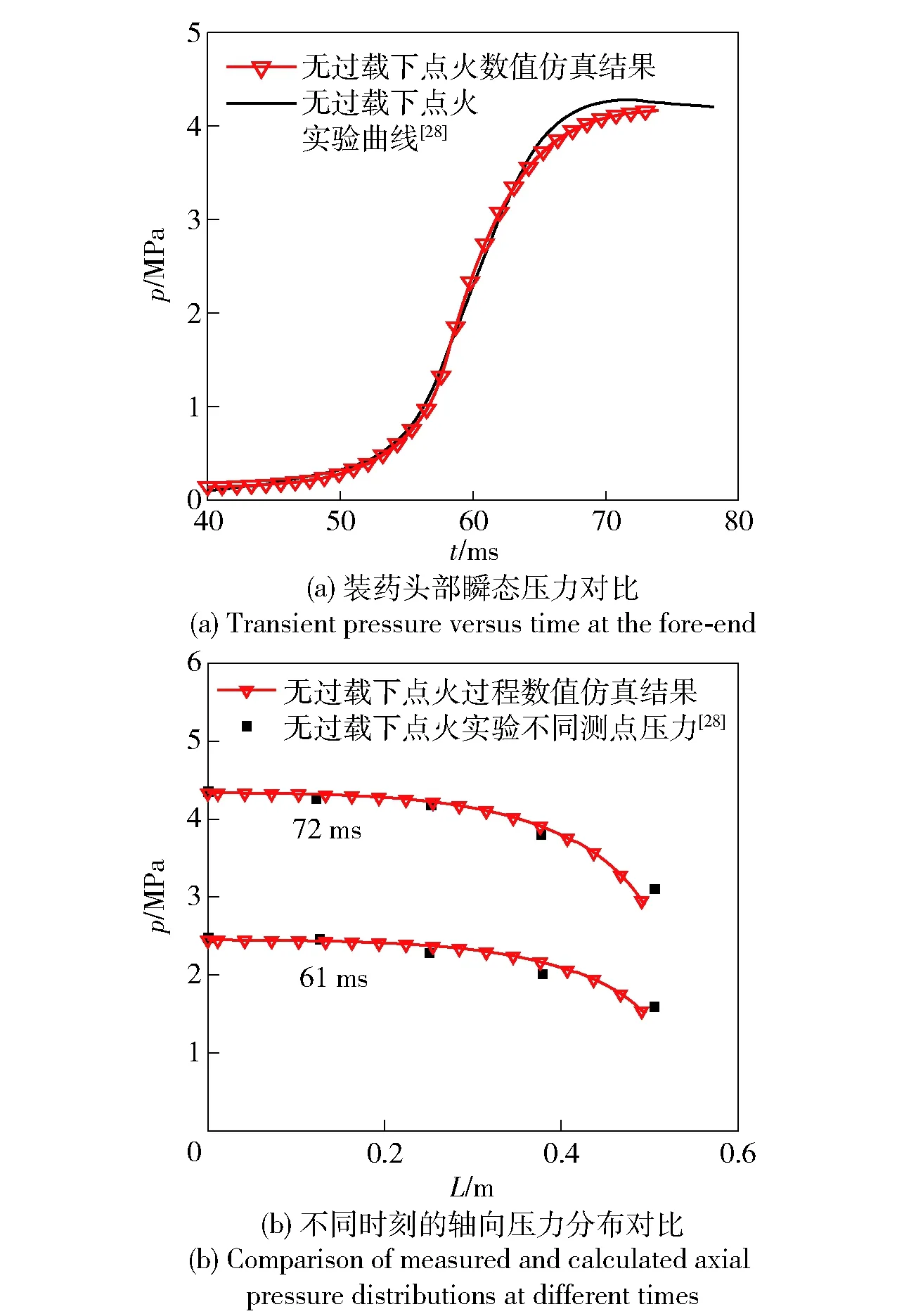
图6 Peretz等实验结果[28]和本文模型计算结果对比Fig.6 Comparison of Peretz’s measured results[28] and numerical results calculated by the proposed model

为了排除网格对过载计算结果的影响，针对文中极端过载100g工况，对不同横/纵节点分布(40×480，60×730和80×950)的3套结构化网格进行网格无关性分析。其中，粗网格(40×480)的Coupled壁面对应的气相第1层网格高度为1×10-4m，中等数量网格(60×730)和精细网格(80×950)的Coupled壁面对应的气相第1层网格高度为5×10-5m. 燃烧室内瞬变升压结果如图7所示。由图7可以看出：3套网格对点火过程的预示差异不大，相较于精细网格的预测结果，粗网格预测压力值在整个建压过程均较小；中等密度网格与精细网格相比，趋势十分接近，峰值压力误差小于2%. 因此在确保计算精度的前提条件下，本文拟在下文中所有算例中采用中等密度结构网格。从无过载点条件点火数值模型结果与实验结果的比较，到添加过载效应模型后点火数值模型的网格无关性验证，目的是保证本文模型预示结果的可信度。

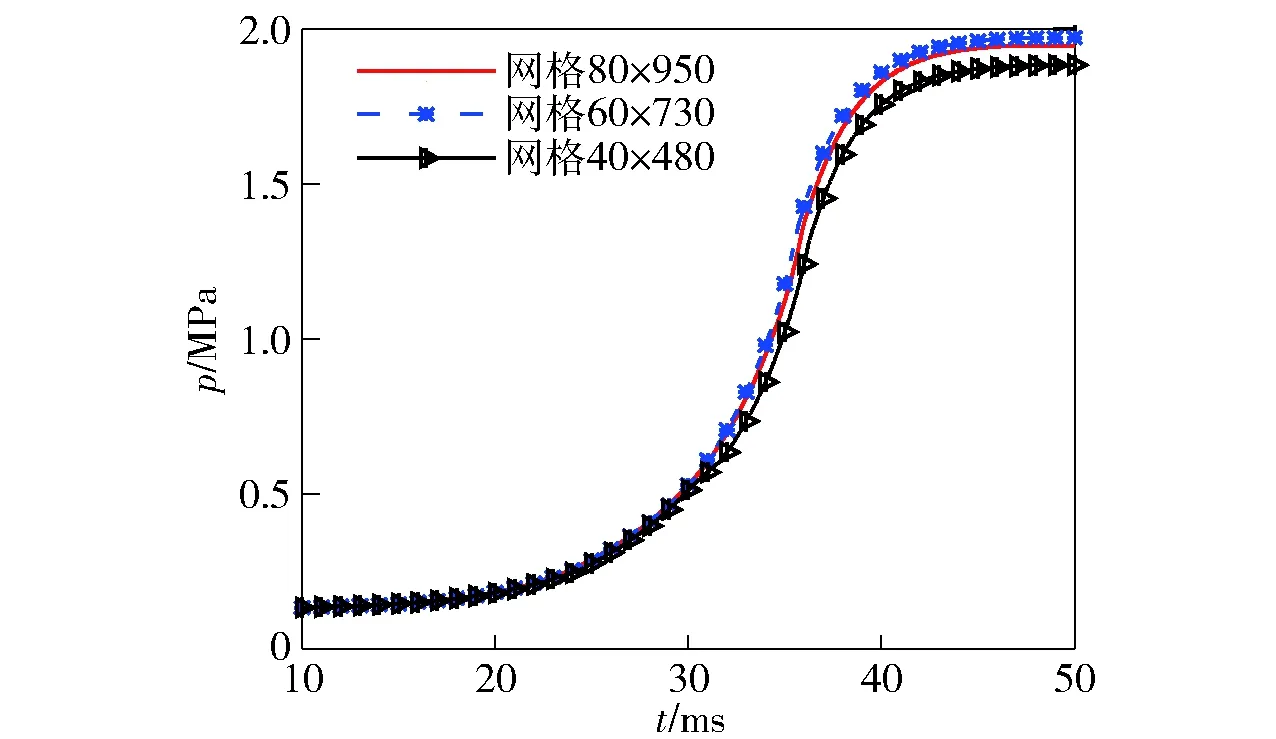
图7 横向过载条件下网格无关性验证Fig.7 Grid independence in accelerative field effect

2 结果分析

2.1 横向过载大小对于点火升压过程影响

图8所示为不同横向过载下点火压力曲线图。图8中，Δp为压力增量，p0g表示0g时的压力。以0g过载压力峰值pmax对各工况下压力进行无量纲处理，从图8中可见：横向过载的出现对点火建压及稳定燃烧整个过程均产生了明显影响，过载导致的压差随时间增长而增大；正向过载作用下的内弹道压力明显高于无过载情况，在100g下，压力增量最高达到117%；负向过载时的燃烧室压力在点火过程中均小于无过载时，-100g时，压力减小量在燃烧稳定时候达到最大，为无过载时的-10%.可见100g对压力值的改变量几乎是-100g时的12倍。由此可以推断：在同一方向过载下，具有对称燃面的固体发动机从点火初始就出现较大的燃烧差异，并随着时间变化表现为累积效果，而这些变化在无横向过载下是不明显的。

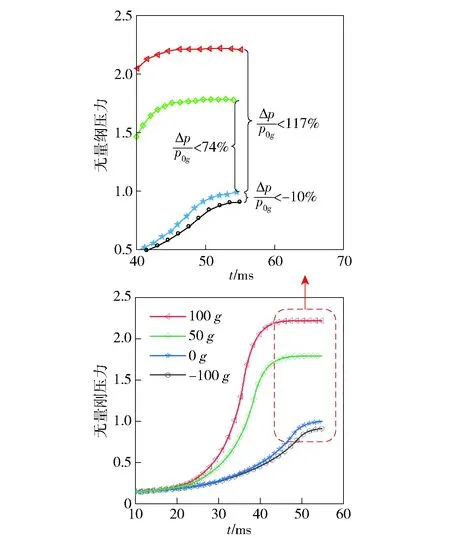
图8 不同横向过载下点火压力曲线图Fig.8 Impact of different radial accelerations on ignition process

与50g相比，100g对燃烧室建压过程影响相对较大。0g到50g的压力增长幅度Δp/p0g为74%，大于从50g到100g的压力增长幅度43%，可以看出：压力增长与加速度现正相关，但压力增速随加速度的增加呈减缓趋势。

图9所示为不同横向过载下点火过程中时刻点分布图。对图9中点火过程3个阶段(点火滞后期、火焰传播期和火焰填充阶段)进行比较：-100～100g5种工况下点火滞后期时间分别为3.51 ms、3.24 ms、3.2 ms、3.05 ms和2.82 ms，可以发现正向过载下点火滞后期缩短。这主要是因为负向过载使得点火燃气远离推进剂表面，削弱对流换热作用，导致推进剂表面在未点燃前热通量下降，到达点火温度时间延长。由于采用纯气体假设且推进剂首次点燃位置靠近点火入口，惯性作用对点火燃气的偏向影响在推进剂头部位置表现较弱，所以点火滞后变化量较小，随着发动机点火燃气颗粒、尺寸和通道宽度的增加，上述变化将会更加明显；-100g～100g5种工况的火焰传播时间分别为45.7 ms、45.5 ms、44.5 ms、35.2 ms和32.6 ms，表明正向过载加速了推进剂燃面火焰传播速度，负向过载降低了推进剂燃面火焰传播速度。从影响程度上看，正向过载对火焰传播时间上的影响大于负向过载；-100～100g5种工况火焰填充时间分别为12.3 ms、11.1 ms、12.0 ms、14.6 ms和16.4 ms，可以发现正向过载引起更高的压力峰值，延长加压填充时间。由于正向过载对点火初期中火焰传播时间的削减大于峰值压力增加引起的填充时间的增加，整个点火过程表现为点火延迟缩短。同一个过载下，对称面燃面在点火初始可能出现燃烧面积不对称的现象，进而存在偏离设计弹道的可能。

图9 不同横向过载下点火过程中时刻点分布图Fig.9 3 stages of inigition process under different radial accelerations

2.2 横向过载对于推进剂燃烧过程影响

图10所示为-100g、0g、50g和100g4种过载下A点、B点和C点由过载/侵蚀两种效应分别引发的相对燃速增量，计算方式依据(13)式和(14)式所示。图10可见：在推进剂前/中部，0g和-100g的Ae和Be相差较小，而推进剂后部Ce在-100g过载下整体略小于0g过载，这是因为负向过载致使燃速下降(Ab、Bb和Cb出现负值，其中，A点处出现最大减少量-13.5%)，削弱上游燃气加注强度，进而减弱了后端的侵蚀过程，这解释了负向过载削弱侵蚀效应的现象；对比100g和0g的Ae，二者差异较小，表明正向过载的出现对推进剂头部侵蚀燃烧的影响较小。对比100g和0g的Ce，二者差异较大，表明正向过载的出现对推进剂后段侵蚀效应的影响较为明显；对比100g和50g，侵蚀燃速Be和Ce在推进剂中后段的影响明显高于过载效应Bb和Cb，但在较高过载时(100g)，推进剂前段过载效应Ab强于侵蚀效应Bb并起主导作用。横向过载条件下，推进剂燃烧将发生变化，被改变程度由燃面所处位置决定，表现为：推进剂前段主要由于过载效应影响，后段主要由侵蚀效应影响；横向过载效应对侵蚀效应的作用是通过影响推进剂头部燃烧而加剧/削弱下游流速，进而加剧/削弱推进剂侵蚀效应实现的。

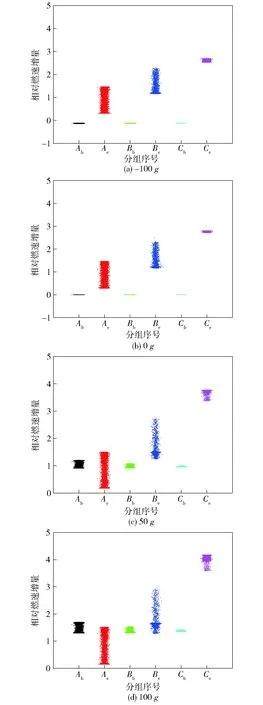
图10 不同横向过载下推进剂不同位置的相对 燃速增量分布散点图Fig.10 Scatter plot of the non-dimensional burning-rate augmentation at different positions of propellant under different lateral accelerations

表3所示为不同横向过载下侵蚀效应/过载效应去量纲燃速增量时变图。表3从时间尺度表明：无论正向过载还是负向过载，燃速变化均出现明显瞬变区和稳态区。将燃速变化率第1次出现小于5%时刻作为瞬态- 稳态转折点，可以发现：过载燃速变化的转折点连线近乎竖直(见表3内各过载效应图中竖直虚线)，表明过载燃速增量在推进剂表面各点出现稳定状态的时间几乎一致；而侵蚀效应引起的转折点根据燃面所处位置靠后而推迟出现。这是因为由侵蚀(5)式和(6)式可知，侵蚀效应由压力、速度和温差等因素决定，在燃烧建立过程中，推进剂通道内流动特性相比压力变化存在滞后，使得侵蚀效应瞬态- 稳态转折点不统一；由横向过载效应(7)式、(8)式和(9)式可知，横向过载效应不受到纵向内流场影响，因此瞬态- 稳态转折点出现时刻差异并不明显。

表3 不同横向过载下侵蚀效应/过载效应的元量纲燃速增量时变图

通过比较图11中100g和-100g时燃速增量占比曲线(计算方式依据(15)式)可以发现：燃速效应所占比重在推进剂燃烧建立过程中是瞬变的；在100g过载下，横向过载效应在推进剂头部的比重逐步增加，当燃烧达到稳定时，由过载效应带来的燃速增量将占比90%，因此正向过载下发动机稳定工作段可以忽略由过载带来的侵蚀效应；-100g过载下，侵蚀效应在初始到稳定各个阶段占绝对主导，推进剂头部受到的过载效应的影响在稳定燃烧阶段出现一定的增加，但占比较少。

图11 不同横向过载下燃速增量占比曲线Fig.11 Ratio of burning-rate augmentation under different lateral accelerations

2.3 横向过载对推进剂火焰传播过程影响

图12所示为火焰传播速度曲线。由图12可以发现：无论是否处于过载条件，火焰传播速度均具有明显的瞬变特性。随着时间推移，火焰传播速度不断增加，在达到峰值过后迅速下降为0 m/s. 100g时，火焰传播速度峰值达到77 m/s，是0g时峰值的2倍；-100g时火焰传播速度峰值低于0过载时的传播速度峰值，二者相差9%. 从火焰传播时间上看，正向过载的出现较大程度地提前了峰值出现的时间，这是因为正向过载加剧了燃烧室上游推进剂的燃烧，点火燃气与推进剂燃气加强下游推进剂的对流换热，而负向过载则延缓了峰值时间的出现，但是延缓程度较小。

图12 不同横向过载下火焰传播速度曲线Fig.12 Flame-spread speed under different lateral accelerations

为了研究普适的规律，在图13中将升压速率、火焰传播速度和燃面面积变化以各自条件下最大值作为归一标准进行无量纲处理，可以发现：火焰传播速度峰值时刻与推进剂表面首次全部点燃时刻以及升压速率峰值点的时刻几乎一致，这意味着无堵盖敞口发动机点火研究中，可以使用实验中获得的压力曲线以及升压速率去分析和判定推进剂表面燃烧状况，降低实验观察难度。

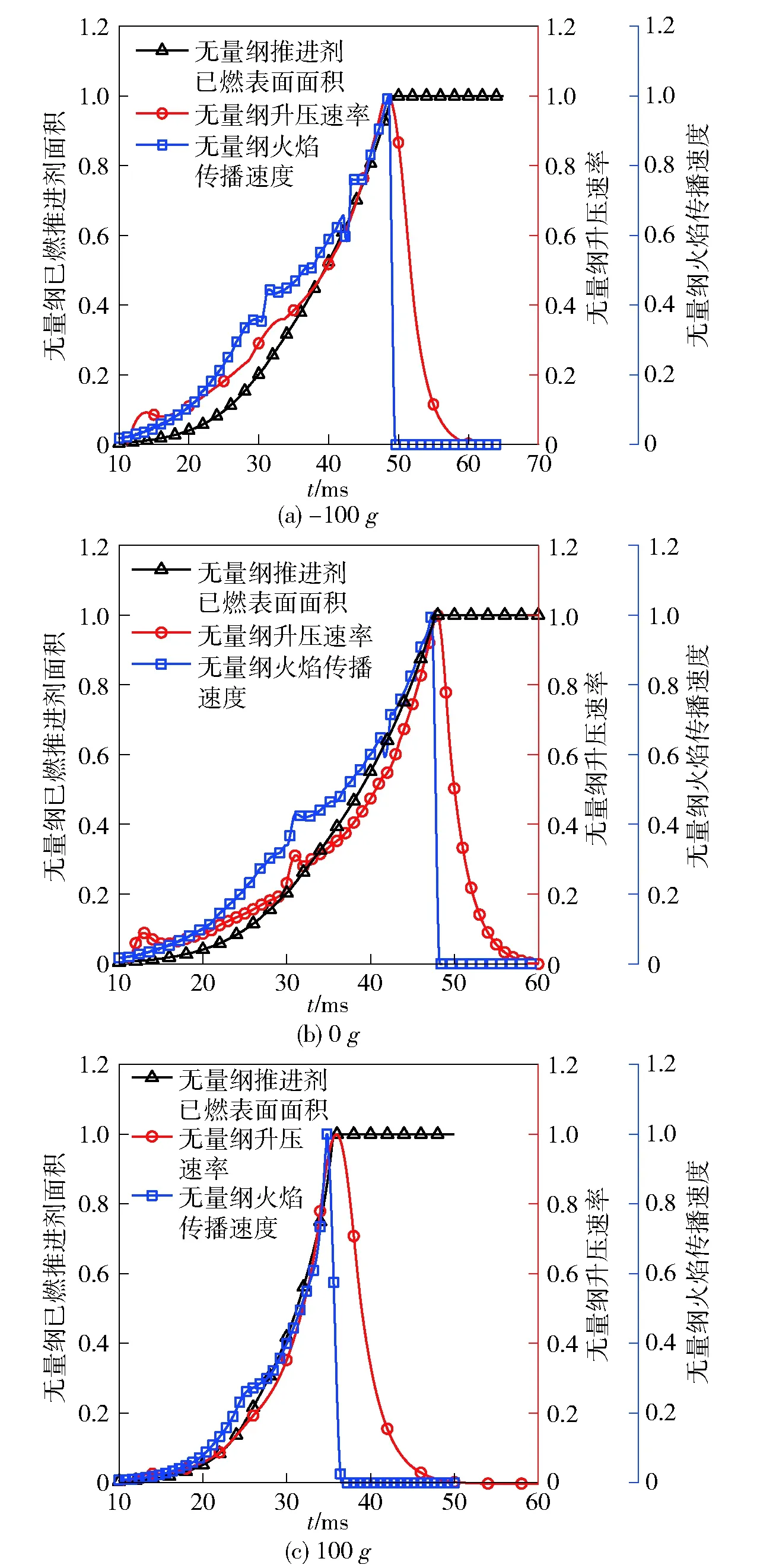
图13 不同横向过载下复合内弹道曲线图Fig.13 Composite interior ballistic curves under different lateral overloads

3 结论

本文构建了单侧推进剂横向过载下的点火过程物理模型，研究和解释了高横向过载下固体火箭发动机过载效应/侵蚀效应耦合规律。通过分析了不同横向过载下火箭点火升压变化规律、燃烧变化耦合机制和推进剂表面火焰传播特性。得到主要结论如下：

1)正向过载下点火压力峰值升高，负过载下点火压力峰值降低。在同一个过载下，内孔型燃面在点火过程将出现燃烧面积不对称的可能，致使实际弹道偏离设计弹道。

2)横向过载对推进剂的燃烧存在影响，影响程度由所处位置决定，主要表现为：正向过载下，推进剂前段燃烧主要由于过载效应影响，后段主要由侵蚀效应影响；负向过载下，过载效应对推进剂燃烧的影响在变化程度和持续时间上均较小。

3)正向过载加剧推进剂前段燃烧，加剧下游侵蚀效应，缩短火焰传播时间；负向过载有削弱侵蚀效应作用，但削弱程度较小。

4)内弹道升压速率可以用来分析推进剂表面燃烧状况，降低实验观测难度。

实际上，发动机尺寸和结构之间的差异将影响上述物理现象的演变程度。本文采用无量纲分析消除了不同条件的幅值差异，所反映规律更客观。使用单侧平面推进剂对横向过载下点火过程进行研究能清晰地反映出侵蚀和过载效应在点火过程的耦合关系，使得该规律具有更强普适性。推进剂在过载下点火过程的研究结论也为工作段过载环境下发动机内弹道研究提供更接近真实的初始条件。