基于LSTM神经网络的管道缺陷模式识别方法研究

谷 晟，别锋锋,郭 越,彭 剑,赵 威

(常州大学 机械与轨道交通学院，江苏 常州 213164)

0 引言

管道作为重要的流体输送工具，其在石油石化、供给排水、天然气等其他流体输送领域中占有非常重要的地位。一旦管道发生故障，将会造成巨大的经济损失，甚至还会引发安全事故，因此对管道状态进行检测与诊断尤为必要[1-2]。但是由于现场环境的复杂性，采集到的管道振动信号往往是非线性，非平稳的。针对如何从非线性，非平稳的管道信号中提取表征管道缺陷类型的故障特征并进行有效的模式识别，国内外学者进行了大量的研究分析。目前，针对管道故障特征提取，最常用的方法是对振动信号进行时频分析。一般，时频分析方法主要包括经验模态分解[3]、小波分析[4]、局部均值分解[5]、核主元分析[6]等。其中，经验模态分解方法[3](EMD, empirical mode decomposition)是处理非线性振动信号的强有力的工具，但是该方法计算效率较低，易造成模态混叠和虚假分量等问题。为了降低模态混叠，文献[7]提出了集合经验模态分解(EEMD, ensemble empirical mode decomposition)方法，虽然该方法可以在一定程度上抑制模态混叠，但计算效率依旧相对较低。随后，文献[8]提出了一种带有自适应白噪声的完全集合经验模态分解(CEEMDAN, complete ensemble empirical mode decomposition with adaptive noise)算法，该算法在EEMD的基础上，既减少了模态混叠又提高了信号的分解效率。

深度学习理论作为机器学习领域的最新研究成果，自提出以来已经在图像识别[9]、语音识别[10]、故障诊断[11]等领域得到了广泛的应用。深度学习方法以数据为驱动，相比于传统的机器学习方法具有更强的特征学习能力，对于分析复杂多变，非结构化的模型具有显著的优势[12]。其中，长短时记忆网络(LSTM, long short term memory)作为一种特殊的循环神经网络(RNN)，它很好的弥补了一般RNN模型中的梯度爆炸及消失等不足，并且对于一些时间序列信息的处理具有较高的自适应性[13]。于洋等[14]针对不同工况下轴承故障声发射信号的辨识问题，基于长短时记忆网络与迁移学习方法构建模型，充分挖掘不同工况下轴承声发射信号之间的关系，从而实现了多工况下轴承故障声发射信号的智能辨识。王鑫等[15]从复杂系统的历史故障数据出发，提出一种基于LSTM的故障时间序列预测模型，并且通过实验证明，该模型在故障时间序列分析中具有更强的适用性以及更高的准确性。陈伟等[16]利用LSTM对时间序列优异的处理能力，将轴承的振动信号数据作为深层LSTM的输入，取得了很好的辨识准确率。王维锋等[17]提出基于LSTM的齿轮故障诊断模型，成功解决了在诊断过程中数据量大、提取特征困难等问题。

本文采用ICEEMDAN-LSTM深度神经网络方法，改进的完全集合经验模态分解方法[10](ICEEMDAN)通过对加入的噪声作进一步优化，可有效的减少信号在分解过程中分量产生的残余噪声和虚假分量等问题。LSTM深度神经网络算法则在分类过程中具有更强的学习和分类能力。因此，针对管道故障特征微弱难以提取的问题，本文提出了一种基于LSTM深度神经网络的管道缺陷模式识别方法。首先利用ICEEMDAN对管道振动信号进行分解生成一系列本征模态分量(IMF)，随后根据相关峭度准则筛选有效IMF分量并计算近似熵作为特征向量集合，然后基于深度神经网络的理论基础构造LSTM深度神经网络模型并对其进行参数优化，最后将特征向量集合导入进行训练和识别。

1 基本原理

1.1 ICEEMDAN算法

ICEEMDAN作为CEEMDAN的改进算法，其主要在CEEMDAN的基础上，在信号进行分解迭代时加入高斯白噪声并且对生成的新的信号求平均。相比较CEEMDAN信号分解方法该方法极大的抑制了信号在分解过程中产生的残余噪声及虚假分量的现象并且有效提高了信号分解效率[18]。其具体的信号分解过程如下：

步骤1:原始信号加入高斯白噪声

(1)

其中：x为原始信号；ω(n)为被添加的第n个高斯白噪声；e1为第一次信号分解时信号的期望信噪比；E1(·)为计算信号的第1个IMF的算子。

步骤2:计算第一次分解的残差r1

(2)

其中:[·]为计算N个信号平均的算子。

步骤3:计算原始信号的第一阶模态分IMF1

IMF1=x-r1

(3)

步骤4:构造第k(k≥2)组加入高斯白噪声的信号

(4)

其中：ek为第k次信号分解时信号的期望信噪比；Ek(·)为计算信号的第1个IMF的算子。

步骤5:计算第K阶残差rk

(5)

步骤6:计算K阶模态分量

IMFk=rk-1-rk

(6)

步骤7:迭代终止条件

(7)

其中:σ为相邻两次IMF分量之间的标准差。令k=k+1,返回步骤4计算下一k值，直至残差满足迭代终止条件。本文采用Cauchy收敛准则，即当相邻两次IMF分量之间的标准差σ<0.2时，迭代终止。

1.2 LSTM神经网络结构

LSTM是一种特殊的循环神经网络(RNN)，它很好地弥补了一般RNN模型中的梯度爆炸及消失等不足。LSTM的主要特征是包含3个门选择结构和一个记忆存储单元结构，其中3个门选择结构分别是遗忘门、输入门和输出门。LSTM靠这些“门”结构让输入特征有选择性的影响神经网络每个时刻的状态[19]。所谓的“门”结构就是使用一个sigmoid作为激活函数的全连接神经网络输出一个0～1间的数值。当一个特征向量输入到LSTM神经网络中训练时，可以根据规则来判断是否有用。只有符合算法认证的信息才会留下，不符的信息则通过遗忘门被遗忘。LSTM的网络结构如图1所示。

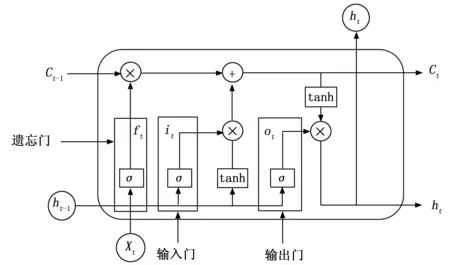
图1 LSTM网络结构图

遗忘门用于判断记忆单元内容是否保留，从而实现对记忆内容的筛选，其输出为：

ft=σ(Wxfxt+Whfht-1+bf)

(8)

式中,ft为遗忘门的输出；σ为激活函数sigmoid;wxf为输入和遗忘门之间的权重；whf为历史输出和遗忘门之间的权重；bf为遗忘门偏置；xt表示t时刻的输入向量；ht-1为前一时刻的输出状态。

输入门用于特征导入并且更新单元状态，当神经网络的其他部分想要写入存储单元的时候，必须先通过输入门。若输入门关闭，则其他神经元就无法把值写入。其输出为：

it=σ(Wxixt+Whiht-1+bi)

(9)

式中,it为遗忘门的输出；wxi为输入和输入门之间的权重；whi为历史输出和输入门门之间的权重；bi为输入门偏置。

另外，在获得遗忘门的输出和输入门输出之后，可以得到当前的记忆单元状态为：

(10)

(11)

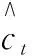
输出门用于控制单元状态的最终输出，并且决定外界的神经元能否把值从存储单元中读出来。单元输出由输出门输出和当前单元

状态信息相乘并经过tanh激活函数得到。故，输出门和单元输出为：

ot=σ(Wxoxt+Whoht-1+bo)

(12)

ht=ottanh(ct)

(13)

式中,ot为遗忘门的输出；wxo为输入和输出门之间的权重；who为历史输出和输出门之间的权重；bo为输出门偏置；ht为当前时刻的单元输出。

2 管道故障诊断流程

本文提出基于LSTM深度学习模型对管道缺陷模式的识别方法，主要分为3个部分：首先，对管道振动数据进行特征提取；其次，建立LSTM模型并对其参数进行优化；最后，利用LSTM模型进行故障识别。具体故障诊断步骤如下：

1)通过多传感器分别采集孔洞、凹坑、裂纹及正常4种不同类型管道在运行状态下的振动信号。

2)对采集到的信号进行ICEEMDAN分解，并提取近似熵作为表征管道运行状态的特征值特征构造特征向量集合。选取其中的80%作为训练样本数据，把剩余的作为测试样本数据。

3)基于深度神经网络理论基础建立LSTM深度神经网络模型，并运用该模型对训练样本数据进行训练，不断调整优化模型中的epoch、batch等参数使训练准确率保持在较高的区间。

4)将测试样本数据输入到训练好的LSTM深度神经网络模型中，实现管道故障的识别。

3 实验及结果分析

3.1 实验平台

为了验证该方法的有效性，利用实验室的管道故障模拟实验平台，分别对管道进行锉刀摩擦，打开泄漏阀，纱布摩擦来模拟工程实际中凹坑、孔洞、裂纹3种管道故障模式以及利用完整的管道来模拟正常模式，并利用水泵向管道通水，当管道处于稳定状态时分别采集管道在这4种运行状态下的振动信号数据。另外考虑到在实际工业过程中，因为长输管线的缺陷位置一般不确定，所以在测试振动信号时传感器的放置位置离缺陷处的位置往往是不确定的，进而导致传感器在不同测点所采集到的管道振动信号特征也会有所不同。在远离缺陷位置如在管道接头处及管卡固定处，由于信号在传递过程中会受其影响，此时所采集到的振动信号特征就会比较微弱。因此，本次实验充分考虑这些实际因素的影响，主要在靠近管卡处、离缺陷位置较远处、靠近激励处等位置布置测点，进行管道振动信号的采集。管道振动信号检测如图2所示。如图所示，实验仪器包括接触式激振器，扫频发生器，压电式加速度传感器、动态信号采集仪及相应的采集软件。首先通过激振器和扫频发生器加强管道运行工况下的振动情况，然后利用加速度传感器在管道上随机布置测点，通过动态信号采集仪及操作PC端采集软件采集管道振动信号。实验室管道系统及3种故障模式如图3所示。

图2 管道振动信号检测示意图

图3 实验室管道平台及故障模式

3.2 数据处理及特征样本集构造

本次实验采集了凹坑，孔洞，裂纹和正常运行4种工况下的管道振动信号，对振动信号进行ICEEMDAN分解。以凹坑管道的一组振动信号为例，如图4所示，为管道振动信号ICEEMDAN分解波形图(前7个分量)，从图4中可以看出，将原始振动信号进行ICEEMDAN处理后的信号冲击特征明显，有利于故障特征的提取。

图4 信号分解结果图

基于ICEEMDAN方法对4种工况下的管道振动信号进行分解共得到12个IMF分量和一个余量。但是，一般在分解过程中得到的IMF分量可能会包含不能够表征管道状态的伪分量，若直接进行特征提取不仅会导致向量集合的维数过多，而且会影响最终的辨识准确率。因此，筛选有效的IMF分量是特征提取的关键。本文根据峭度准则计算峭度值以此来筛选出最能表征不同工况下管道运行状态的IMF分量。如图5所示，为各阶IMF分量峭度值变化趋势。一般，正常平稳运行且噪声干扰小的信号，其峭度值大于3。从图5中可以看出，前七阶IMF分量的峭度值呈逐渐降低的趋势且数值大小都大于3，因此选取IMF1-IMF7分量进行后续的特征提取分析。

图5 各阶IMF峭度值变化趋势

针对管道缺陷信息的特征提取，本文预从时频域特征进行分析处理，从而构造特征样本集合。信息熵是一种非线性估计方法，主要通过量化的熵值对非稳态信号的复杂性程度进行衡量。信息熵理论作为特征提取的方法之一，广泛应用在对有噪声夹杂信号中有效信息的提取。它实际上是一个描述如设备运行的复杂程度、诊断的难易程度等无法明确量化确定的指标。故本文最终选取信息熵论中的近似熵作为表征4种工况下管道状态的特征集合。另外，本次实验所采集的管道振动信号样本共计4个类别，分别为正常、裂纹、孔洞及凹坑。在样本数据采集过程中，采样时间设置为60 s。每种工况下的管道振动信号为1 000组，总样本数为4 000组。以每种工况下管道振动信号样本数据中的一组数据为代表，图6分别展示了4种工况下管道振动信号的近似熵在空间上的特征分布情况。

为了直观地显示特征提取的效果，选取ICEEMDAN分解的前3个IMF分量来分析特征向量在三维空间上的聚类情况。选取特征近似熵的三维空间特征分布如图6所示，从图中可以看出4种工况下管道振动信号的特征分布均呈现云状分布，其中有部分样本特征发生重叠现象。这是因为近似熵作为信息熵的一种，主要用来对信号特征的无序性与复杂性进行描述。一般正常运行的管道其在运行过程中受到的冲击较少，因此正常管道的振动信号的熵值较大，无序性也较高。当管道中出现诸如孔洞、凹坑、裂纹等缺陷时，其在运行过程中的冲击特征就会增强，相应的管道振动信号的无序性就会变低。反应到特征值的空间分布上，虽然可以初步达到聚类的效果，但是样本特征重叠较多，尤其是针对凹坑、裂纹、孔洞管道的样本特征值。因此，对管道振动信号进行特征提取后，需要做进一步的深层次的分析处理才能实现对管道状态的有效识别。

3.3 LSTM深度神经网络分类模型设计

针对不同缺陷类型管道微弱特征难以识别的问题，本文建立了LSTM深度神经网络分类模型。整个神经网络由输入层(Input)；隐含层(LSTM层，full connect layer层)和输出层(Loss)组成。数据由输入层流入，经过LSTM神经网络并使用Tanh激活函数非线性化，再流入全连接层并使用Sotfmax函数激活，最后输出。本文主要按照以下3个步骤设计网络结构。

第一步：构建LSTM深度神经网络模型。LSTM深度神经网络结构设计如图7所示，LSTM层激活函数(activate function)选择Relu函数，全连阶层激活函数选取Softmax函数，输入层即特征处理的特征向量。

图7 基于LSTM的深度神经网络结构设计

第二步：计算损失函数(loss function)大小。损失函数描述的是神经网络计算结果和实际结果之间的误差，最终的目标是通过梯度下降使得找到一组合适的权值和偏置值使得损失函数的值最小。常见的损失函数有均方差损失函数和交叉熵损失函数[20-21]。本文将会比较均方差损失函数和交叉熵损失函数的训练结果，最后选择适合管道缺陷深度学习模型的损失函数。

第三步：寻找一种方法快速确定各个神经元的权值和偏置值，即通过优化器(optimiter)确定合适的参数，使得整个网络模型得到一个相对满意的结果。在损伤识别过程中，本文比较了4种优化器(adagrad、adadelta、mini batch gradient descent、momentum)对于损失函数收敛性和最后识别准确率的影响，最后选择出合适的优化器。

4 管道特征信号的LSTM深度神经网络模式识别

本文针对对凹坑、孔洞、裂纹和正常4种状态的管道振动信号各提取了1 000组，共4 000组数据。每组数据采样2 048个点。训练样本为在每种状态中选取800组样本数据，剩余的200组作为测试样本。另外，比较均方差损失函数与交叉熵损失函数对于训练模型的影响，最终分析选择交叉熵损失函数。为了防止训练过程中出现过拟合问题加入了Dropout。其他的具体参数如表1所示。

表1 编程参数

图8和图9分别展示了深度神经网络的识别准确率和损失函数的大小。从图8及图9中可以看出，损失函数的值前20步迅速下降，此时模型距离全局最小值较远，梯度快速下降，反应到准确率图上就是前20步迭代过程准确率迅速提高，迭代了20步左右整个神经网络模型就有一个不错的识别准确率，损失函数逼近于全局的最小值，此时梯度下降变缓，在整个模型的全局最小值附近做一个缓慢的调整，在准确率识别图的反应就是迭代多个周期以后准确率才有一个缓慢的提升。当迭代80步时整个模型相对稳定趋于全局最小值处，因此本模型的迭代步数设置为100。另外，单独从图8中可以看出参数优化过后的神经网络识别准确率达到了95%。而且分类的准确率随着训练不断提高的过程中没有出现明显的振荡，这说明本模型的学习率设置合理。从图9中可以看出，损失函数在快速下降后趋于一个收敛的值，说明模型结构和参数设置合理。

图8 LSTM深度学习模型准确率

图9 LSTM深度学习模型损失函数

将特征样本集输入LSTM深度神经网络分类模型中，得到如图10所示的分类结果图，其中1、2、3、4分别代表孔洞、凹坑、裂纹、正常4类标签。从图10可以看出，训练集、测试集及验证集对4种不同缺陷类型的管道识别准确率基本达到了95%左右。而且该模型总的分类效果从图10中所有混淆矩阵中可以看出达到了95.3%，其中对于标签4即正常管道运行状态的辨识准确率达到了100%，标签1的识别率达到了99.2%，因此本模型的误差主要集中在标签2(识别准确率为92.5%)和标签3(识别准确率为89.6%)的分类识别上。

图10 训练集、测试集和验证集混淆矩阵

本模型的误差的区间为[-1,1]，将误差区间均分为20份，作出模型的数据误差直方图，如图11所示。图中展示了模型训练完后样本训练集、样本测试集和样本验证集的误差。从图11中可以看出误差主要分布在[-0.05,0.05]，这说明了该神经网络模型对于分类识别处于一个较小的误差水平，同时也进一步表明所提出模型的结构稳定且对不同工况下管道故障检测具有很好的识别效果。

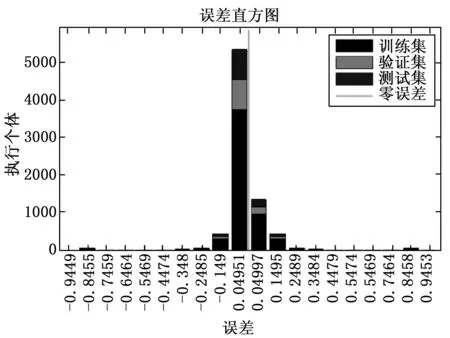
图11 误差分析

5 结束语

针对管道振动信号特征微弱难以提取的问题，本文提出了一种基于LSTM的深度学习神经网络模式识别方法。首先利用ICEEMDAN信号分解方法分解管道振动信号，该方法很好地克服了管道振动信号在分解过程中产生虚假分量和模态混叠的问题，对复杂的振动信号具有很好的分解效果。然后根据峭度准则选取前7阶IMF分量并且构造近似熵特征向量集合。最后根据LSTM深度学习理论构造LSTM分类模型并对该模型中的参数进行优化，将特征向量集合导入LSTM深度神经网络中进行模式识别。实验结果表明：基于LSTM的深度神经网络模型能够较好的应用于管道故障检测领域，而且故障识别准确率可达95%，显著提高了对不同工况下管道故障检测的辨识准确率。