三维数据关联情况下外辐射源雷达多目标跟踪研究

李晓花 李亚安 金海燕 鲁晓锋

①(西安理工大学计算机科学与工程学院 西安 710048)

②(陕西省网络计算与安全技术重点实验室 西安 710048)

③(西北工业大学航海学院 西安 710072)

1 引言

信息技术的迅猛发展使作战双方围绕电磁频谱控制权的争夺日趋激烈，为克服传统主动式雷达的不足，目前世界大国均开展了外辐射源雷达的研究[1,2]。外辐射源雷达目标跟踪，是指雷达系统对目标反射的其他非合作照射源信号(如电视、导航、通信、卫星信号等)进行处理，实现目标的跟踪[3,4]，该系统具有隐蔽性好、信号源丰富、抗杂波能力强等优势[5–7]。

外辐射源雷达跟踪系统的量测信息主要包括距离、角度和多普勒信息[8]。单独依靠某一种量测信息进行外辐射源多目标跟踪具有一定局限性，由于外辐射源雷达跟踪系统的角度测量误差较大，本文采用距离和多普勒相结合的方式开展外辐射源雷达多目标跟踪研究。

由于直达杂波、多径干扰、同频干扰等信号的存在，外辐射源雷达跟踪系统容易出现数据关联错误问题[9–11]。针对该问题，Deming等人[12]利用修正期望极大化(Expectation Maximization,EM)方法在目标和量测之间进行EM迭代来估计目标状态，目标后验概率易收敛于局部最大化。基于数据关联的多目标跟踪算法，如动态多维分配(dynamic multidimensional assignment)[13]和联合概率数据关联(Joint Probabilistic Data Association,JPDA)[14,15]，采用最直接的方法进行目标和量测的多维分配。Daun等人[16,17]通过建立多目标局部航迹提出了多假设跟踪(Multiple Hypothesis Tracking,MHT)似然比跟踪方法，在距离-多普勒域处理数据关联问题，需要进行坐标域的转换。Tobias等人[18]提出外辐射源雷达多目标粒子概率假设密度(Probabilistic Hypothesis Density,PHD)算法，去杂波性能较好，由于需要粒子重采样，计算量较大。Pikora等人[19]将基于随机有限集(Random Finite Set,RFS)理论的高斯混合PHD和高斯混合势概率假设密度(Gaussian Mixture Cardinality PHD,GMCPHD)算法应用于外辐射源多目标跟踪问题，可以联合跟踪目标状态和目标数量。杨威等人[20]对基于随机有限集的目标跟踪技术进行了综述。为降低运算量，基于EM方法的PMHT算法假设一个目标可以产生多个量测信息，从而得到最大后验概率意义下的跟踪[21–25]。

本文利用PMHT算法的独立性假设条件，引入一个新的关联变量表示发射机-量测之间的数据关联关系，提出一种新的3维数据关联(目标-量测-发射机)情况下的改进PMHT算法。为了增加数据关联的准确性，提高多目标与量测、发射机后验关联概率的精确度，将距离-多普勒量测设为均值相同协方差不同的混合高斯分布。针对距离-多普勒量测的非线性性，采用无迹卡尔曼平滑(Unscented Kalman Smoother,UKS)算法[26,27]对多目标状态进行估计。对FKIE外辐射源雷达数据集进行仿真实验，结果表明，对于密集雷达杂波环境，改进算法具有很强的剔除杂波能力，算法误跟率低，表明算法的有效性。

2 系统模型

2.1 目标状态模型

其中，um(t)为外辐射源跟踪系统的过程噪声，Fm(t)是跟踪系统的状态转移矩阵。

2.2 量测模型

其中，wm(t)为跟踪系统量测噪声，h(xm(t),ps)为量测函数。

t时刻的距离和多普勒量测分别为

其中，f0为发射机的辐射频率，c为声速。

3 外辐射源改进PMHT算法

3.1 PMHT算法

设X为待估计变量集，Y为可观测变量集，K为不可观测变量集，则X的最大后验概率可表示为

其中，E{·}表 示求期望，p为概率密度函数。

在实际问题中，直接求解式(5)非常困难，PMHT算法的优点是避免直接求解此公式。定义如式(6)

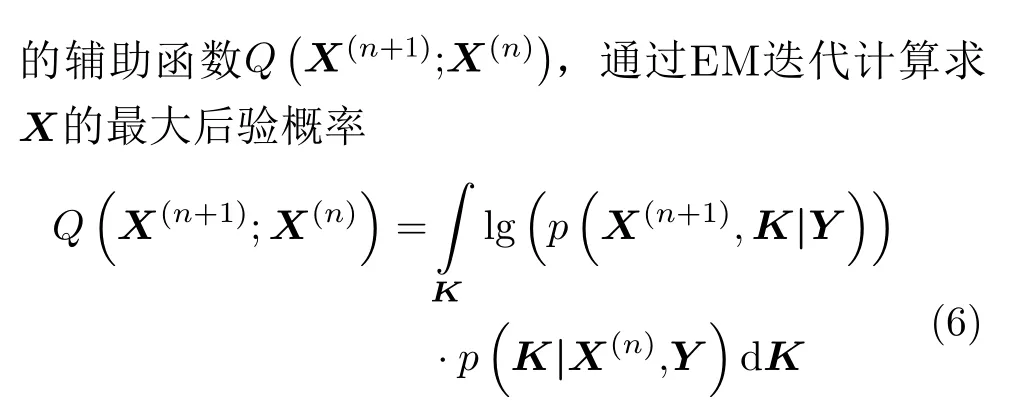
其中，上标n是EM迭代次数。

PMHT算法的特征是所求变量X的后验概率密度随着EM迭代次数n的增加单调递增，经过多次EM迭代后算法收敛，得到X的最大后验概率。因此，X的最大后验概率可表示为

3.2 3维数据关联改进PMHT算法

图1给出了PMHT算法和改进PMHT算法的数据关联过程。如图1所示，改进PMHT算法通过增加关联变量j来解决量测-发射机数据关联关系。

图1 PMHT算法和改进PMHT算法数据关联过程示意图

设量测-目标、量测-发射机之间数据关联关系的先验概率分别为

其中，合成量测和合成量测协方差分别为

将此合成量测和协方差作为新的量测，利用UKS算法得到各个目标的状态估计值。

算法实现过程如下：

步骤1 设定EM迭代次数。

步骤4 计算多目标后验关联概率。对每个发射机s和 目标m，由式(20)计算各个目标的后验关联概率。

步骤5 计算各个目标的合成量测和协方差。对每个发射机s和目标m，由式(24)和式(25)计算合成量测和协方差。

步骤6 计算各个目标sigma点的协方差和各个目标的滤波增益。

步骤7 滤波计算。对每个目标m和发射机s，由合成量测和协方差更新各个目标状态和

步骤8 循环EM迭代直到算法收敛。

步骤9 向前更新滑动窗并返回步骤3。

4 实验仿真

4.1 仿真场景设置

为了验证所提算法的有效性，对FKIE雷达数据集进行仿真实验，此数据集的网络1由2个静止发射机和1个接收机组成，处理10个匀速直线运动目标[21]。接收机位于坐标原点，发射机位置分别为[29434 m,–34761 m,293 m]和[12845 m,–106922 m,293 m]，发射频率均为500 MHz。杂波个数服从泊松分布，均匀分布于量测空间，每个采样周期内杂波的平均个数为79。采样周期为1 s，检测概率为0.8，跟踪时间为200 s，Monte Carlo仿真次数250次。过程噪声强度为5 m2/s3，距离和多普勒噪声协方差分别为50 m和20 Hz。10个目标的初始位置和速度如表1所示。

表1 目标初始位置和初始速度

4.2 仿真结果分析

图2给出了多目标真实轨迹和本文算法的估计轨迹，可以看出，本文算法估计轨迹与各个目标真实轨迹相近，可以很好地跟踪上10个目标。图3给出了密集杂波情况下的距离-多普勒量测和所提算法的合成量测，以及无杂波情况下的量测值，可以看出，雷达杂波密度很高，本文所提算法的合成量测与无杂波环境下多目标跟踪量测趋势基本一致，说明3维数据关联改进PMHT有良好的抗杂波性能。这是因为本文算法通过利用量测-目标、量测-发射机两个数据关联变量来表示量测-目标-发射机之间的3维数据关联关系，降低了数据关联模糊性，提高了算法的杂波抑制能力。

图2 基于距离-多普勒的多目标跟踪真实轨迹和本文算法的估计轨迹

图3 密集杂波情况下距离-多普勒量测和所提算法的合成量测，以及无杂波情况下的多目标量测值

图4和图5分别给出了3维数据关联关系未知时本文算法和PMHT算法对10个目标的位置均方根误差，可以看出，本文算法对10个目标的位置均方根误差总体小于PMHT算法，从图2也可以看出所提算法可以较好地跟踪上10个目标，说明了本文3维数据关联改进PMHT算法的跟踪有效性。

图4 本文算法对10个目标的位置均方根误差，3维数据关联关系未知

图5 PMHT算法对10个目标的位置均方根误差，3维数据关联关系未知

表2给出了本文所提算法和PMHT算法对10个目标的速度平均均方根误差。从表2可知，本文算法的速度平均均方根误差为2.32 m/s，PMHT算法的速度平均均方根误差为5.72 m/s，本文所提算法相对于PMHT算法具有较低的误跟踪率。这是因为所提算法通过增加数据关联变量增强了多目标与量测、发射机的数据关联准确性，同时通过将量测设定为多个均值相同协方差不同的混合高斯分布，提高了多目标与量测后验关联概率的精确度，从而提高了跟踪精度。

表2 本文算法和PMHT算法速度平均均方根误差(m/s)

表3给出了不同EM迭代次数下本文算法和PMHT算法跟踪采样200次的运行时间，可以看出，随着EM迭代次数的增加两种算法的运行时间均增加，计算得出当EM迭代次数最大时，单位采样时间内的运行时间为0.57 s，通过仿真发现，当EM次数为6时，所提算法即可收敛，可以满足跟踪实时性要求。

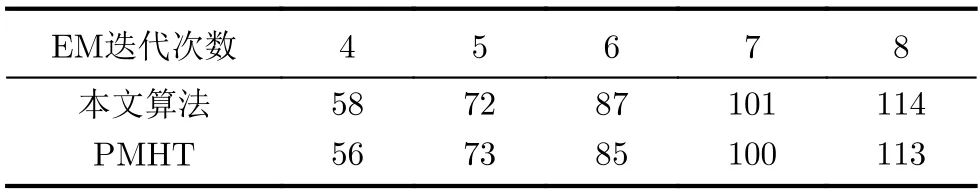
表3 采样200步的跟踪运行时间对比(s)

为了评估所提算法的稳定性，本文采用平均归一化估计误差平方(Average Normalized Estimation Error Squared,ANEES)作为评价指标[28,29]，

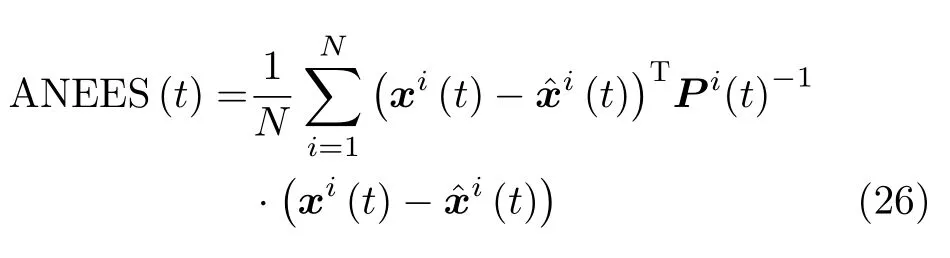
其中，N为蒙特卡洛仿真次数，xi(t)为第i次蒙特卡洛目标状态真实值，为第i次蒙特卡洛目标状态估计值，Pi(t)为目标状态协方差矩阵。

ANEES定义为利用目标状态协方差矩阵对目标状态误差平方进行归一化，理想情况下，其均值等于目标状态的维数。所提算法对10个目标的ANEES如图6和表4所示，由图6可以看出，初始时刻10个目标的ANEES较大，随着跟踪时间的推移，平均归一化估计误差平方减小并且稳定，从表4计算得出跟踪扫描时间内平均ANEES的值为3.806，在理想平均ANEES 95%的置信区间内，说明本文算法具有良好的跟踪稳定性。

表4 10个目标的平均归一化估计误差平方(ANEES)

图6 10个目标的平均归一化估计误差平方ANEES

5 结论

外辐射源雷达具有隐蔽性好、信号源丰富、抗杂波能力强等优势。不同于传统多目标跟踪问题，除了量测-目标数据关联模糊问题外，外辐射源雷达跟踪系统新增了量测-发射机数据关联模糊问题，即数据关联关系是3维的。针对此问题，本文引入一个新的关联变量来表示发射机和量测之间的数据关联关系，提出了改进的目标-量测-发射机3维数据关联PMHT算法。通过将距离-多普勒设定为均值相同协方差不同的混合高斯分布提高了多目标跟踪精度。针对距离-多普勒量测非线性问题，采用UKS算法进行多目标状态估计。仿真结果表明，对于外辐射源FKIE雷达数据集，所提算法有很强的抗杂波性能。