基于代价参考粒子滤波器组的检测前跟踪算法

卢 锦 王 鑫

(陕西科技大学电子信息与人工智能学院 西安 710021)

1 引言

延长观测时间是雷达中检测微弱目标的有效方法。但在较长的观测时间内，目标机动性等给信号积累带来困难。例如，在天波雷达中，在较长的观测时间内，目标处在同一个检测单元内，但转向或加速等使目标回波具有复杂的调频特性，可模拟为未知的非线性调频信号[1–4]。此种情况下，长时间信号积累检测微弱目标的问题，即是检测低信噪比的非线性调频信号的问题。

国内外学者提出了很多检测非线性调频信号的方法，从检测结果看，可将这些方法分为两类。第1类，基于非线性调频信号的状态估计结果累积观测数据，通过门限比较实现给定虚警率下的检测。文献[5]中的脊能量检测方法和文献[6]中的时频分布累积方法，都是沿瞬时频率曲线在频域累积观测数据能量实现目标检测。此外，文献[7]基于粒子滤波(Particle Filter,PF)构造观测数据的联合似然比，文献[8,9]基于代价参考粒子滤波(Cost-Reference Particle Filter,CRPF)和FB-CRPF(Forward-Backward CRPF)构造累积代价，也是通过累积观测数据的能量实现目标检测。第2类方法主要是基于PF的检测前跟踪(Track-Before-Detecting,TBD)方法(PF-TBD)[10,11]。此类方法在目标状态向量中增加表示目标存在状态的离散变量，估计各个时刻的目标存在概率，当存在概率大于给定门限时，即判断目标在该时刻存在。

上述两类方法中，第1类方法虽然可提供给定虚警概率下的目标检测，但无法判断目标出现和消失的具体时刻；第2类方法虽然能够判断目标出现和消失的具体时刻，但采用存在概率描述检测能力，较难用常规的检测概率和虚警概率衡量算法性能。

上述两类方法的关键都是非线性调频信号的瞬时频率估计，瞬时频率估计精度与检测能力直接相关。PF类方法用大量带有权值的随机样本近似目标状态的后验概率密度函数，可提供更准确的非线性调频信号瞬时频率估计，广泛应用于雷达信号处理、图像处理等领域[12–16]。但PF类方法的状态估计精度与收敛速度直接相关。通常，非线性调频信号检测问题的先验信息非常有限，导致PF类方法的收敛速度较慢。此外，有限的先验信息要获得较好的估计结果，就需要大量样本，大量的样本必然带来巨大的计算量。而PF类算法的并行化执行一直是一个难题。因而，在先验信息非常有限的情况下，收敛速度和计算复杂度是限制PF类检测方法的主要因素。

针对PF类算法收敛慢和计算复杂度高的问题，本文提出一种具有完全并行结构的CRPF[17,18]，即CRPF滤波器组(CRPF bank)。基于CRPF滤波器组的估计结果，分别累积各段观测信号，将各段的累积能量与给定门限比较，实现给定虚警概率下目标在各个时刻的目标检测。仿真结果表明，与现有的PF-TBD方法相比，本文提出的方法检测能力强，运行速率高。

2 代价参考粒子滤波器组

2.1 状态空间模型

以天波雷达为例，假设在观测时间t∈[0,Tob]s内，目标处于一个检测单元中。此时目标检测问题可归结为如式(1)的二元假设检验问题

若 H0成立，则目标不存在，观测z(t)仅包含未知的背景噪声w(t)；若H1成立，则目标存在，观测z(t)是 未知的非线性调频信号s(t)与未知的背景噪声w(t)的混合，如式(1)所示。目标检测问题就是根据观测z(t)来 判断H0成立或H1成立。

若采用基于PF的方法处理上述二元假设检验问题，则要先假设 H1成立，在此基础上建立状态空间模型来估计目标状态。本文提出的CRPF滤波器组也是一类PF算法，因此需要建立状态空间模型。下面，假设 H1成 立，将回波信号s(t)近似为分段线性调频信号来建立状态空间模型，以估计s(t)的瞬时频率。

基于式(9)和式(10)的状态空间模型，非线性调频信号的瞬时频率曲线估计问题转化为从观测序列ZK={z1,z2,...,zK}中估计状态序列X={x1,x2,...,xK}。基于状态估计结果和观测序列，可进行目标检测。

2.2 CRPF滤波器组的结构

基于2.1节的分段调频信号状态空间模型，本节提出CRPF滤波器组来快速、准确地估计非线性调频信号的瞬时频率。图1是CRPF滤波器组的基本结构，包括M个并行的CRPF，每个CRPF采用相同的状态空间模型，如式(9)、式(10)所示，但先验信息不同。

图1 CRPF滤波器组的结构

(4)比较M个CRPF的累积代价，将累积代价最小的CRPF的估计结果作为CRPF滤波器组的估计结果。

显然，步骤(1)—步骤(3)可并行执行。因此，CRPF滤波器组的运行时间Ttotal为

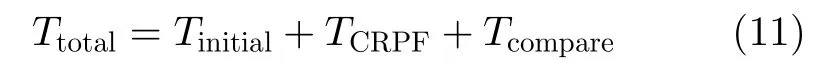
式中，Tinitial表示计算第m个CRPF的更精确的先验信息的计算时间，TCRPF表示第m个CRPF的运行时间，Tcompare表示比较M个累积代价的时间。

2.3 计算详细的先验信息

那么如何为第m个CRPF设计更精确的先验信息呢？本节详述此问题。

从式(8)的系统方程可得关系

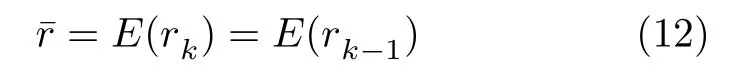
此外，由式(8)可从多普勒频率估计调频率

结合先验信息f(t)∈[fmin,fmax]，由式(13)可得调频率的均值的可能范围为

将式(14)中调频率均值的可能范围，近似为调频率的可能范围，则与先验信息r(t)∈[rmin,rmax]相比，有以下3种情况：

图2比较了3种不同情况下假设的先验信息与原有的先验信息f(t)∈[fmin,fmax]Hz的比较，阴影部分是基于情况(1)至情况(3)获得假设的先验信息。可见，在分段线性调频信号及具体的初始时刻频率的假设下，假设的先验信息更详细。

图2 假设的先验信息与原始先验信息的对比

2.4 CRPF滤波器组伪码

本节给出CRPF bank中第m个CRPF的伪码，对应2.3节的情况(1)、情况(2)，以及情况(3)的第p段子观测区间。

3 基于CRPF滤波器组的TBD算法

针对式(1)描述的检测问题，本节提出一种基于CRPF滤波器组的目标检测策略，可在给定虚警概率下，判断目标在各个时刻是否出现，如图3所示。

由图3可见，基于CRPF滤波器组的检测策略包含以下3个步骤：

图3 CRPF滤波器组-TBD的检测策略

4 仿真

4.1 测试信号

为了证明CRPF滤波器组在运行速度、信号检测性能方面的优越性，本文采用两类测试信号

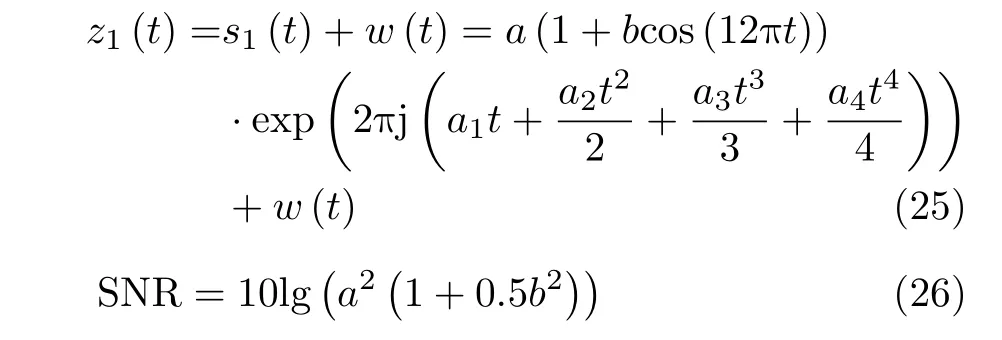
式(25)中，a(1+bcos(12πt))表示时变的信号幅度，b∈[0,1),a1,a2,a3,a4∈[-20,20] 。w(t)服从方差为1，形状参数为0.5的复广义高斯分布[19]。观测信号的信噪比(Signal to Noise Ratio,SNR)如式(26)所示。

式(27)中，b∈[-40,40]，观测信号的信噪比如式(28)所示。

4.2 CRPF滤波器组-TBD的检测性能和瞬时频率估计性能

图4和图5所示分为SNR=–9 dB,–7 dB,Pfa=0.001时，对3种测试信号，CRPF滤波器组-TBD,PF-TBD[10]和Rutten PF-TBD[11]在各个时刻的检测概率Pd和瞬时频率曲线的均方根误差RMSE(Root Mean Square Error)。其中瞬时频率曲线的RMSE定义如式(29)所示。式(29)中，f表示测试信号的瞬时频率，表示瞬时频率的估计，Ls=Tob/ts表示观测序列的长度。仿真中，CRPF-滤波器组-TBD包含2000个CRPF，每个CRPF仅用1个样本，PF-TBD和Rutten PF-TBD的样本数是6000。PF-TBD和Rutten PF-TBD在各个时刻的检测概率计算如下：将各个时刻的存在概率当作检测统计量，根据虚警概率确定检测门限，当存在概率大于检测门限宣布目标存在，否则宣布目标不存在。此时，3种方法的检测结果可直接比较，同样的虚警概率下，检测概率大者，检测能力更强。

图4 3种测试信号的检测概率及瞬时频率RMSE比较

图5 3种测试信号的检测概率及瞬时频率RMSE比较

表1是PF-TBD,Rutten PF-TBD和CRPF滤波器组-TBD的平均单次运行时间。PF-TBD和Rutten PF-TBD的单次运行时间是指其处理一个观测信号得出检测结果的时间。CRPF滤波器组-TBD的单次运行时间是其中一个CRPF的运行时间、多个CRPF的累积代价的比较时间、各段信号积累的时间以及门限比较的时间之和，运行时间单位为s。表1表明，CRPF滤波器组-TBD的运行时间仅为PF-TBD的千分之一。

表1 本文的CRPF滤波器组-TBD与PF-TBD,Rutten PF-TBD的运行时间(s)比较

本节的仿真结果表明，本文提出的CRPF滤波器组-TBD方法的检测和估计能力均优于同类方法，且复杂度更低，运算时间更短。

4.3 目标出现时刻及持续时间对CRPF滤波器组-TBD性能的影响

本节分析目标出现时刻及持续时间对CRPF滤波器组-TBD,PF-TBD及Rutten PF-TBD性能的影响。图6所示是第2种测试信号，SNR=–7 dB,b=0.1，目标出现在t∈[0.25,0.75]s时，PF-TBD，Rutten PF及CRPF滤波器组-TBD在各个时刻的检测概率和瞬时频率曲线RMSE，以及目标出现在t∈[0.125,0.4375]s时，PF-TBD,Rutten PF及CRPF滤波器组-TBD在各个时刻的检测概率和瞬时频率曲线RMSE。仿真结果表明，3种方法的检测能力和瞬时频率估计能力对目标出现的时刻及持续的时间都不敏感。但CRPF滤波器组-TBD的检测能力状态瞬时频率曲线估计精度均远高于PFTBD及Rutten PF-TBD方法。

图6 目标出现时刻及持续时间对3种方法的检测概率及瞬时频率RMSE的影响

4.4 CRPF 的数量、样本数及子区间长度对CRPF滤波器组-TBD性能的影响

本节分析CRPF的数量、样本数量及子区间长度对CRPF滤波器组-TBD性能的影响。图7所示是第2种测试信号，SNR=–7 dB,b=0.1，目标出现在t∈[0.25,0.75]s，每个CRPF 只用1 个样本，CRPF滤波器组-TBD包含的CRPF的数量分别为50,100,500,1000,2000,2500,3000时，CRPF滤波器组-TBD的检测概率和瞬时频率曲线RMSE比较。仿真结果表明，随着CRPF的数量增加，CRPF滤波器组-TBD的检测能力和估计能力会缓慢增加。当CRPF的数量大于2000后，CRPF滤波器组k-TBD的检测和估计能力基本稳定。

图7 CRPF的数量对CRPF滤波器组-TBD检测性能和估计性能的影响

图8所示是第2种测试信号，SNR=–7 dB,b=0.1，目标出现在t∈[0.25,0.75]s，CRPF滤波器组-TBD包含2000个CRPF，各个CRPF采用的样本数分别是N=1,5,10,20,50,100时，CRPF滤波器组-TBD的检测概率和瞬时频率曲线RMSE比较。仿真结果表明，随着样本数的数量增加，CRPF滤波器组-TBD的检测和估计能力会下降。即在其他条件一样的情况下，样本数为1时CRPF滤波器组-TBD的检测能力和瞬时频率估计能力最好。

图8 样本数对CRPF滤波器组-TBD检测性能和估计性能的影响

5 结束语

本文提出了一种具有并行结构的非线性调频信号瞬时频率估计方法CRPF滤波器组，并在此基础上提出了可同时在各个时刻检测目标和估计目标状态的检测前跟踪算法CRPF滤波器组-TBD。CRPF滤波器组-TBD基于CRPF滤波器组的状态估计结果，计算每个观测子区间内观测信号的增量代价，将增量代价作为各个时刻目标检测的检测统计量。当某一时刻的增量代价大于给定门限时，即认为该时刻目标出现。与常规的基于粒子滤波TBD方法相比，CRPF滤波器组-TBD方法可提供各个时刻的恒虚警检测。仿真结果表明，CRPF滤波器组-TBD方法的检测性能、估计性能及运行速度均优于同类方法。