抓住问题 培养学生计算思维
2021-10-30毛佳秋
毛佳秋
摘要:计算思维是高中信息技术学科最为关键的核心素养之一,对培养学生创新和终身学习等能力很有帮助。作者提出,在实际教学实践中,教师应善于发现问题,找准契机,想办法、找对策,在教学中搭建学生与计算机之间沟通的桥梁,促使学生像计算机科学家、计算机一样思考问题,让他们自觉地用计算思维去发现问题、思考问题、解决问题,并在这种持续、反复的过程中强化计算思维。
关键词:计算思维;二进制;数据
中图分类号:G434 文献标识码:A 论文编号:1674-2117(2021)20-0000-02
● 提出问题
早前在网上看过一则笑话:
小A在一家互联网公司实习,有一天,工作结束,小A回到宿舍,心中闷闷不乐的样子。
朋友小B见状关心到:怎么了?有什么不愉快的事情吗?
小A叹了口气,说:今天在我写的程序中做了一个计算,然后出了个“Bug”,被测试的人笑了,说我竟然连0.1+0.2都不会算。
小B忍不住笑了:0.1+0.2=0.3,这你也能算错?
小A不服道:这不能怪我,谁知道计算机那么笨,居然不能把0.1+0.2算对,不信你看,结果竟是0.30000000000000004。
● 教学过程
笔者以“0.1+0.2≠0.3”这一问题为契机,通过它的求解过程让学生理解计算机中数据的表示及相关运算的過程,有意识地深度培养学生的计算思维。
在学习相关内容之前,学生理解的计算就是1+1=2、10-1=9这样的十进制运算。但是自计算机成型以来,所有的数据都是以二进制形式表示的,计算机内部所进行的存储、运算也都是以二进制的形式进行的。而且我们身边还有很多其他的数据表示和运算规则,如中国古代重量单位的换算——半斤八两,这类以十六进制形式进行运算。另外还有时分秒这样的“六十”进制、玛雅人的“二十”进制等。
“进制”实际上就是进位计数制,它是用一组固定的符号和统一的规则来表示数值的方法,通俗地讲,就是做加法时“逢几进一”的规则。
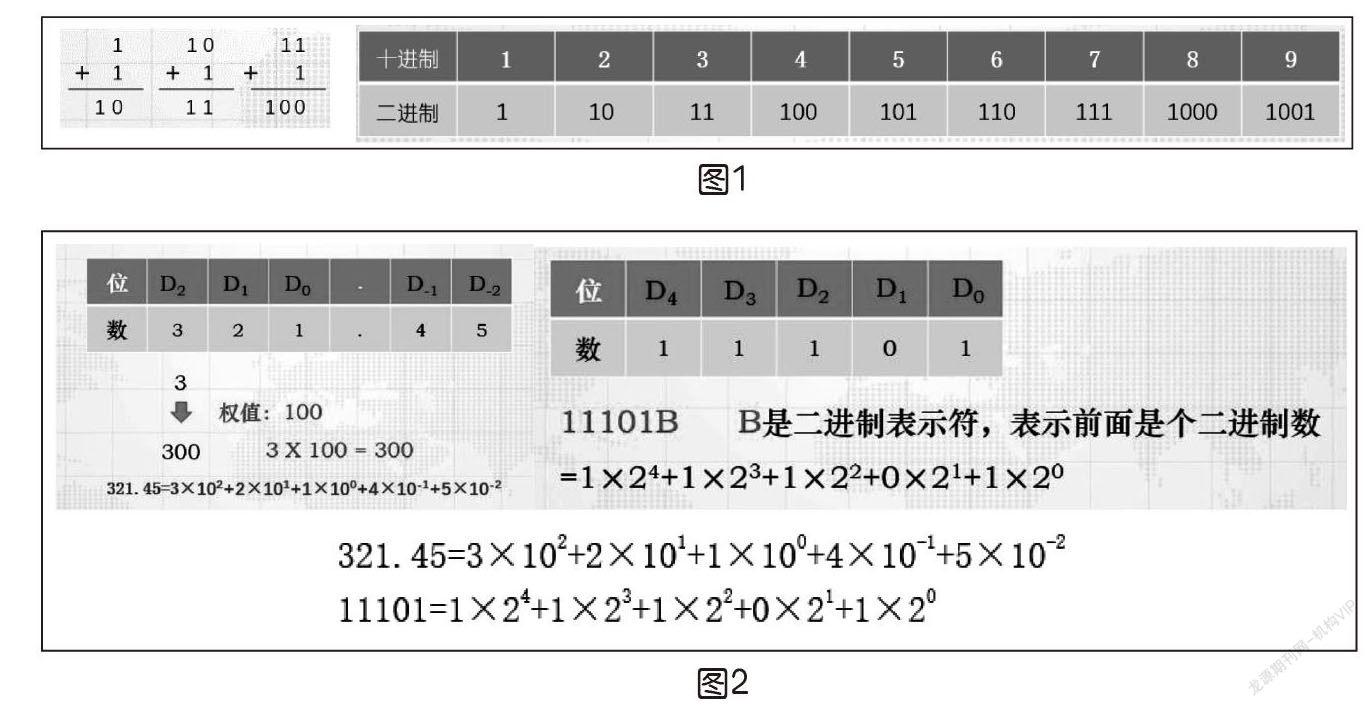
这时学生也就明白了为什么十进制1+1是等于2,而二进制1+1却等于10,这不仅迈出了解决问题的第一步,更迈出了通向计算机世界的第一步(如上页图1)。
接着,随着数的一步一步累加,学生自然会思考有没有什么通用的法则、规则来表示十进制数,这就会涉及十进制与二进制转换的知识。这种思考的过程正是逻辑思维的过程与方法——计算思维。
当跨出第一步后,接下来就可以开始学习“二进制、十进制的表示”,了解“位”“权”“权值”的概念,掌握每个数符所表示的值等于数符本身乘以它所在位的权值这一基础概念(如上页图2)。
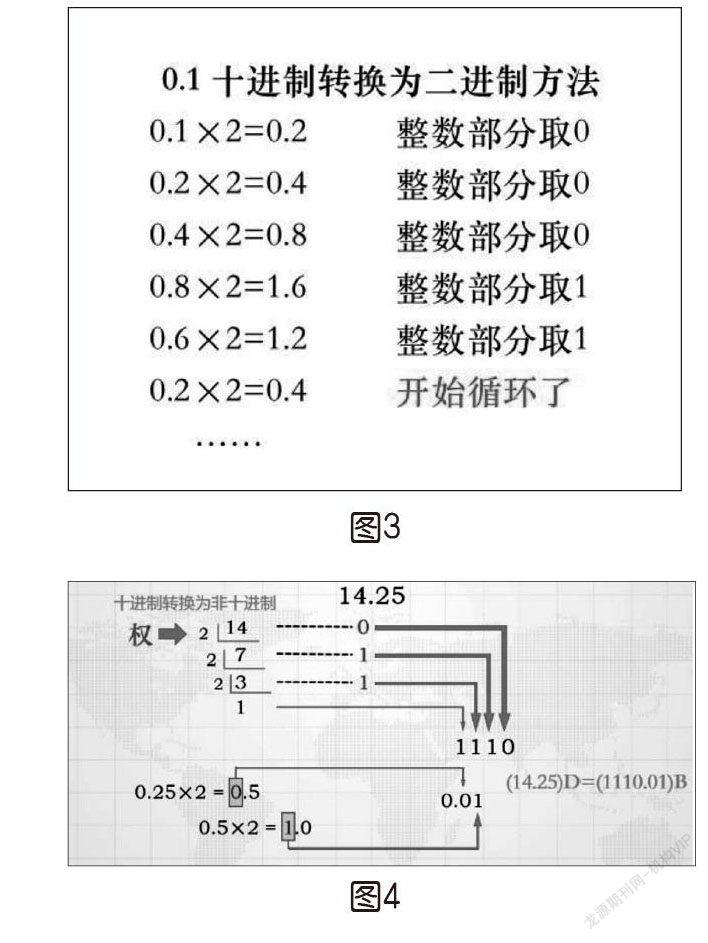
然后就是二进制、十进制的转换,通过实践学习牢记计算转换规则。整数部分:除权取余,直到商为“0”,倒序排列;小数部分:乘权取整,正序排列(如图3)。
很显然,在转换小数的时候,并不是所有数字多次乘以2就能得到整数,部分数字会产生无限循环,0.1和0.2就是这样(如图4)。
一个不精确的二进制数字参与运算,得到的也将是不精确的结果,这就是0.1+0.2≠0.3的原因。学生也就明白了为什么计算机在计算0.1+0.2时会出现运算“出错”的情况。接着,教师可以继续引导学生思考显示位数及计算精度问题,这就涉及数的精度等问题。这一过程不仅能让学生循序渐进地掌握相关知识、概念、原理,培养学生的动手操作能力,还能引导学生将计算思维合理地应用到日常生活和学习中,形成一种思维习惯,锻炼学生综合应用所学知识主动发现问题和解决问题的能力。
● 结语
教师培养学生的计算思维,实际上是培养学生像计算机科学家、计算机一样思考问题,通过将一个个具体问题及其解决方案表达成计算机可以处理的形式,并设计计算的方式,将客观世界解释为一个复杂的信息处理过程。
通过“0.1+0.2≠0.3”这类问题,让学生明白在解决日常生活中问题时,解决方案是否可行,甚至比它是否在理论上存在更加重要;明白正确性和可行性的关系——知道什么叫巧妇难为无米之炊;明白“理论”与“实际”、“实验室结果”和“日常使用效果”的差距与差异。
单一的理论学习无法培养学生的计算思维,必须通过大量的实践来培养。教师要搭建学生与计算机之间沟通的桥梁,引导学生将无意识的计算思维变成有意识的行为,让他们自觉地用计算思维去发现问题、思考问题、解决问题,在这个持续、反复的过程中将其内化、升华。
参考文献:
[1]中华人民共和国教育部.普通高中信息技术课程标准(2017年版)[M].北京:人民教育出版社,2018.
[2]王克胜.高中信息技术教学中学生计算思维培养存在的问题及对策[J].中国现代教育装备,2020(10):29-32.
[3]巴军.搭建现实与“用计算机解决”之间的桥梁——浅谈信息技术课堂教学中计算思维能力的培养[J].中小学信息技术教育,2020(11):48-50.
