利用混合模型CRBM-PSO-XGBoost识别致密砂岩储层岩性

2021-10-29谷宇峰张道勇鲍志东

石油与天然气地质 2021年5期

谷宇峰，张道勇，鲍志东

[1.自然资源部油气资源战略研究中心，北京100034； 2.中国石油大学(北京) 地球科学学院，北京102249]

准确获取储层岩性数据对于开展地层对比、沉积展布分析和地质建模等地质基础工作至关重要，因此岩性识别一直被视为是一项关键研究内容[1-6]。经典的岩性识别工具为交会图。交会图一般是由2种或3种测井曲线构成的，而选取的曲线需要对各种所需识别的岩性都能有独特的响应范围[4-6]。故而，当测井数据点散落在交会图中，各个岩性对应的测井响应划分条件便可通过观察来明确。对于砂质较纯或者岩性成分简单的储层，该工具能够有效地解决其岩性识别问题，但随着油气勘探范围的扩大，非常规油气逐渐成为了油气研究方向上的核心对象，使得更多关于非常规储层的岩性识别问题被提出。由于非常规储层岩性成分复杂，且多数岩性在测井曲线上具有相似的响应特征，导致以交会图为代表的经典识别工具难以适用，为此众多地球物理学家发展了以机器学习技术为主的岩性识别方法[7-15]。

机器学习是人工智能的一个重要分支，其主要计算原理是在对学习数据分析的基础之上，建立自变量与因变量的线性或非线性网络映射关系，之后根据该关系完成对预测数据的处理。在模式识别领域，目前得到广泛应用的模型有KNN(K-nearest neighbors)，PNN(probabilistic neural network)和SVM(support vector machine)等[7-15]。KNN模型是聚类分析中的代表，主要是依据预测数据点与学习数据点之间距离的远近进行模式判断。由于不需要对学习数据进行训练，所以KNN模型计算效率较高，而且因为预测数据点只会被聚类到距离最近的学习数据点的模式中，所以即使学习样本中含有少量错误样点，该模型仍能够进行有效的判断，体现出其容错能力。赵彤彤等(2018)使用了一种基于模糊熵的KNN模型进行了岩性识别研究，并取得了较好的识别效果[7]。张梓童等(2019)分析了KNN模型的计算原理，并通过验证明确了该模型在岩性识别上是一种有效手段[8]。PNN模型是一种基于概率密度分析模式的识别模型，其主要思想是先利用学习样本建立各个模式的概率密度分布，之后根据预测样本在分布中的概率值判断归属。由于该模型采用了概率分析，较KNN模型在学习样本处理上有更高的容错性，而且概率密度分布的建立无需训练，所以理论上其预测效率也较高。赵杰和李春华(2009)在岩性识别中尝试了PNN模型，并取得了不错的识别效果[10]。陈刚(2018)以随钻测井资料为基础，利用PNN模型对煤层岩性进行了识别，验证了模型的有效性[11]。SVM模型是监督学习中的代表，其主要计算思想是先通过训练找到影响模式判断的最重要的学习样本(称为支持向量)，之后依据这些样本完成数据预测。由此可见，该模型的预测效率和预测效果完全取决于支持向量的数量和质量，而不是通过全部样本学习的，这就大大提升了模型的容错能力和计算效率。李政宏等(2020)分析了机器学习技术在岩性识别中的重要性，并证明了SVM模型是一种有效识别模型[13]。根据SVM模型的特性，林香亮等(2020)使用PCA(principal component analysis) 模型对其进行改进，并验证了PCA-SVM混合模型在砂砾岩岩性识别上具有良好的应用效果[14]。虽然上述模型在许多应用案例中都得到了一定程度的认可，但仍难以推广。由于每个预测样本都要和所有学习样本进行计算，所以随着学习样本容量的扩大，KNN和PNN模型的计算效率将会严重降低；随着学习样本维度的增加，样点间的距离值也会随之增大，从而加大了KNN模型在模式判断上的不确定性；建模需要多种经验参数参与，如PNN模型的概率密度分布窗口长度和SVM模型的惩罚系数等，导致预测模型和预测结果难以确保为最优。

梯度提升是一类优秀的模式识别技术，其主要计算原理是先将目标值与计算值之间的差值作为训练对象，再通过一系列CART(classification and regression tree)回归树训练将差值减小，最后凭借由这些训练后的回归树组成的强学习器完成预测[16-19]。XGBoost模型是这类技术的代表。由于该模型引入了正则化项，并精细化了学习公式，所以在训练过程中大概率地避免了过拟合现象的发生，确保了训练的可靠性；由于融入了并行计算技术，模型的计算效率不会随着训练样本容量的扩大而出现严重衰减的现象。因此，该模型因其训练稳定且计算效率高在岩性识别中也得到了关注[16-19]。Dev 和Eden (2019) 利用了该模型进行了岩性识别，并验证了模型的有效性[18]。闫星宇等(2019)采用XGBoost模型研究了渗透率预测和储层评价问题，发现该模型的应用对于测井解释发展具有重要意义[19]。但需注意，XGBoost模型在建模过程中也有两点不足：建模需要较多经验参数参与，使得模型状态难以确保为最优；当样本维度变高时，为提高计算效率，模型可通过自身的随机自变量采样技术来实现，但这种随机处理方式也会使得建模后模型状态难以确保为最优。为使XGBoost模型在建模后达到最佳状态，本文采用PSO (particle swarm optimization)模型和CRBM (continuous restricted Boltzmann machine)模型对其进行改进。PSO模型能有效解决参数优化问题，而CRBM模型因具有数据提取功能可从源数据中挖掘出更少且对因变量预测更为重要的新自变量，由此解决了样本随机降维的问题[20-25]。至此，本文提出利用CRBM-PSO-XGBoost混合模型来解决非常规储层岩性识别问题。下文将对模型的计算原理和预测效果逐一分析。

1 计算原理

在本文中，由于岩性识别问题是利用由测井资料和岩性观察数据建立的模型来解决，因此学习数据集中自变量应由测井曲线构成，而应变量由岩性观察数据构成，可表示为A={Xmn,Ym}，其中Xmn为测井数据矩阵，表示有m个样本，而每个样本由n条曲线构成，Ym为岩性观察数据向量，有m个样本。岩性观察数据在程序中为字符信息，难以应用，为此采用one-hot coding(独热编码) 技术进行编码[16-19]。例如，岩性观察数据为细砂岩，与之对应设定的原始编码为2，而识别的岩性共有5种，则最终采用的编码是一个长度为5且第二个元素为1的零向量，可表示为[0,1,0,0,0]。所以，Ym在编码后可进一步变为YmK，其中K为识别岩性种类，也是每个样本的长度。此时，因变量的样本可表示为yi=(yi1,yi2,…,yiK)。XGBoost模型采用CART回归树进行迭代训练，并在训练后形成一个预测模型。预测模型称为强分类器，其表达式如下[16]：

(1)

式中：Fk(xi)为作用在样本xi上的第k类强分类器，i=1,2,…,m；wjk,d为在第d次迭代中第k棵回归树(即第k类回归树)的第j个叶节点中所有样本的替代值，无量纲，k=1,2,…,K，d=1,2,…,D，j=1,2,…,J；η为学习速率，无量纲。

以公式(1)为基础，确定样本xi被分到第k类岩性的概率由下面的softmax函数计算[16-19]：

(2)

式中：Probk(xi)表示概率值，无量纲。

在所得的概率值中选择最大值对应的岩性标记为样本xi的预测岩性。公式(1)中的wjk,d由下式确定[16-19]：

wjk,d=-Gjk,d/(Hjk,d+λ)

(3)

(4)

(5)

式中：xi∈Rjk,d，Rjk,d为在第d迭代中第k棵回归树的第j个叶节点对应的区域；fk,d-1(xi)为在第d-1次迭代中作用在样本xi的第k类学习器，其形式以公式(1)为准；L为损失函数，一般以交叉熵形式为主，在本文中为-yilln[Pl,d-1(xi)]，P为公式(2)所示的softmax函数；λ为正则化系数，无量纲。

由于XGBoost模型在应用前要设置好框架，其中有较多经验参数需要确定，如迭代次数、回归树分裂次数、正则化系数和学习速率等，因此建模后模型难以确保在最优状态。本文采用在多目标最优化问题上计算效率高的PSO模型对其进行优化。在执行PSO模型之前，先要设定种群[20-22]。种群包含许多种子，而每个种子由需要优化的参数构成，所以种群可表示为：

Γ={σi|σi=(σ1i,σ2i,…,σzi),i=1,2,…,q}

(6)

其中，q为种子数量，σi为第i个种子，包含z个参数。之后，PSO模型通过下面的迭代公式计算各参数的最优值[20-22]：

(7)

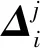
为计算方便，公式(7)中计算结果和目标结果应以原始编码组成。前人研究结果显示，在迭代前期采用较大的ω有利于全局搜索，而到后期采用较小的ω有利于局部搜索，为了能够让PSO模型高效地进行优化计算，本文采用LDIW(Linear decreasing inertia weight)算法使ω能够在迭代中自适应地改变[20-22]。

XGBoost模型计算效率一般随着样本中自变量个数的增加而降低，因此Chen 和 Guestrin (2016)在创造该模型时为提高其运行速率提出了自变量随机采样算法[16]。该算法是在考虑自变量较多时，随机选择几个自变量重组学习样本，以让XGBoost模型能够通过处理容量更小的学习样本来快速建模。由于自变量是随机选的，难以保证这些自变量都能影响因变量的变化，为此本文提出采用CRBM模型方法对源数据进行处理，以实现在源数据降维的同时确保得到的新自变量都为关键变量。CRBM模型是通过连接可见层和隐含层之间的权重将源数据进行转换，以此实现自变量由多变少的目的[23-25]。为确保转换质量，CRBM模型一般要将提取的特征或者称新自变量反转化到可见层中，并将重构的数据与源数据进行对比，此时如果两者之间的误差在允许的范围内，则表明转化是有效的。CRBM模型的框架一般可表示为[23-25]：

(8)

式中：P为概率激活函数，由S函数(即sigmoid函数)确定；V为可见层数据矩阵；W为权值矩阵；H为隐含层数据矩阵；vi为第i个可见层数据向量；hj为第j个隐含层数据向量；σ为设定的噪音方差，无量纲；N为以标准正态分布为准的噪音，无量纲；φh和φl为S函数的上、下渐近线；μ为噪音控制参数，无量纲，当减小时能够让S函数从确定状态变为二值随机分布状态；θ为迭代参数集，即在迭代中需要确定的参数集。

公式(8)表明源数据可通过第一分式转到隐含层中，而隐含层数据可通过第二分式转回到可见层，用于检验重构数据质量。公式(8)中需要确定的参数有W和μ，因此θ只包含该两个参数，对应的迭代公式为[23-25]：

(9)

式中：Δwij,k为W第i行第j列元素在第k次迭代中的迭代步长，无量纲；Δμk为在第k次迭代中μ的迭代步长，无量纲，k=1,2,…,K；右上角标0和1分别表示迭代开始前的可见层数据和由隐含层重构得到的可见层数据。

(10)

公式(10)表明由隐含层重构的可见层数据将在处理最后一个mini-batch后得到。在确定步长之后，并在融合mini-batch技术情况下，CRBM模型的迭代公式可表示为[25]：

(11)

式中：ξ为动量系数，无量纲。

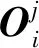
2 实验验证

2.1 数据来源及实验设计

本次实验以姬塬油田西部长4+5段(延长组4+5段)致密砂岩储层为验证对象。姬塬油田处于鄂尔多斯盆地中西部天环坳陷和陕北斜坡两个一级构造单元之间，其整体构造形态呈一宽缓的北东-南西倾向的单斜(图2)[26-29]。油田发育多个含油层系，其中长4+5段是主力开发层系之一。长4+5段为浅水三角洲沉积，主要发育三角洲前缘亚相，其储层的形成受控于沉积展布，多为水下分流河道、水下天然堤和河口坝[26-29]。油田西部目前共有2 000多口探井和评价井，但只有少部分井具有岩心资料，因此为完成长4+5段的精细地层格架建立和沉积展布规律分析等工作，岩性识别成为一项关键研究内容。根据多口探井的岩心资料观察，识别出目的层储层主要岩性共8种，分别为中砂岩、细砂岩、粉-细砂岩、粉砂岩、泥质粉-细砂岩、泥质粉砂岩、粉砂质泥岩和泥岩。依据经典交会图的设计原理，本次选用测井数据中显示孔隙性的AC(声波时差)、含泥性的GR(自然伽马)和含油性的AT90(阵列感应电阻率)来划分岩性。图3a为AC-GR-AT90三维交会图，可见8种岩性的测井数据点在图中融杂在一起，难以进行区分。图3b—d为3种曲线两两组合形成的二维交会图，同样，各个岩性的数据点在图中仍有很大程度上的重合，导致划分标准难以建立。图3表明目的层的主要岩性不能由二维或三维交会图进行识别，其原因是多种岩性具有相似的测井响应特征，使有效的岩性-测井响应识别关系无法形成。为此，本文采用机器学习方法来解决岩性识别问题，并根据在引言中的分析提出一种新的混合模型CRBM-PSO-XGBoost。模型结构及其计算流程已经在计算原理中进行了说明，并用图1进行了展示，这里不再赘述。

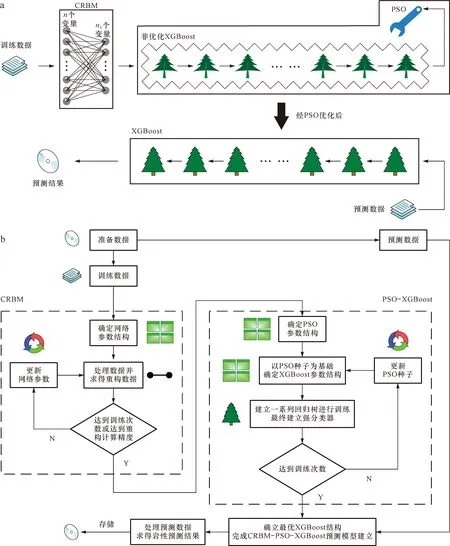
图1 CRBM-PSO-XGBoost模型结构(a)及其计算流程(b)Fig.1 Structure(a)and computing flow (b) of the CRBM-PSO-XGBoost,a hybrid model proposed

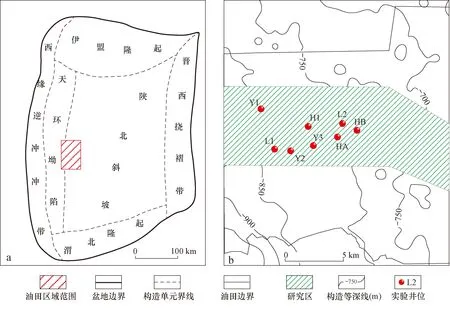
图2 鄂尔多斯盆地构造区划(a)及姬塬油田西部工区概况(b)Fig.2 Structural division (a) and outline of western Jiyuan oilfield (b), Ordos Basin

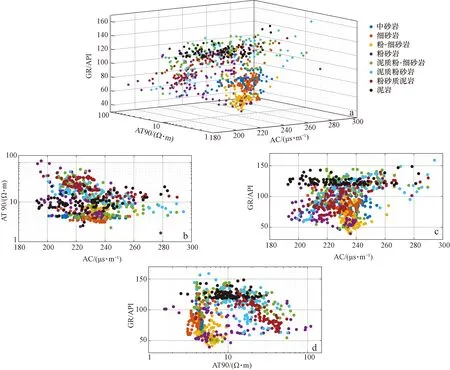
图3 用于识别目的层8种主要岩性的三维和二维交会图Fig.3 3D or 2D cross correlations used to identify 8 major types of lithology of target formationsa. AC-GR-AT90三维交会图；b. AC-AT90二维交会图；c. AC-GR二维交会图；d. GR-AT90二维交会图

为验证所提出模型的预测能力，本文采用研究区8口取心井的测井及岩心观察数据进行实验，井位如图2c所示。岩心观察数据是根据每一个测井深度点对应从岩心柱上观察所得到的岩性数据。Y1，Y2，Y3，L1，L2和H1井设为训练井，即利用这些井的资料组成学习样本，而HA和HB井设为验证井，即利用两口井的资料组成预测样本。学习样本共4 606个，而预测样本每口井有300个。样本由测井曲线和岩心信息组成，其中测井曲线有11种，分别是AC(声波时差)、SP(自然电位)、GR(自然伽马)、CNL(补偿中子)、DEN(补偿密度)、PE(光电吸收截面指数)和阵列感应电阻率(AT10，AT20，AT30，AT60，AT90)。岩心信息为岩心观察数据的原始编码经one-hot coding技术转换后得到的信息。本次规定中砂岩、细砂岩、粉-细砂岩、粉砂岩、泥质粉-细砂岩、泥质粉砂岩、粉砂质泥岩和泥岩对应的原始编码依次为数字1到8。所以，针对某一测井深度点，如果从岩心上观察到的岩性为细砂岩，则与之对应的原始编码为2，岩心信息为[0,1,0,0,0,0,0,0]。为简易说明，岩心信息在表中用原始编码进行了展示。实验共有两个，其中第一个实验是利用由Y2，Y3，L2，H1资料组成的含有3 060个样本的学习数据进行预测，第二个是利用全部学习样本进行预测，其目的是检验预测模型的识别准确率是否会在增加训练样本量的情况下有所提升。为增强验证效果，实验中加入了PNN和SVM模型进行对比。

2.2 实验过程及结果

在实验1中，先验证XGBoost模型是否在嵌入PSO模型和CRBM模型后其预测能力有所改变，之后再对所有预测模型进行对比。对于XGBoost模型，一组根据前人研究成果设定的经验参数如表1的第3列上部分所示。进行优化前，PSO模型的计算参数也要设定。一组经验参数展示在了表1中部。需要指出的是，PSO模型较XGBoost模型更容易找到一组理想的设置参数，这是因为PSO模型目的就是将模型参数进行调优以确保预测结果最为可靠，而这点很容易在PSO模型迭代计算中实现，即在不动XGBoost模型预先设置参数的情况下，PSO模型可通过简单的参数调试甚至不用参数调试即可令XGBoost模型参数达到最优化，所以PSO模型的嵌入虽然增加了预先设置参数的工作量，但在实际操作上减少了调参工作量[20-22]。对于CRBM模型，一组设定的经验参数如表2所示。

为使PSO-XGBoost混合模型更快速地完成建模，CRBM模型应从源数据中提取更少的特征，因此依据前人研究经验，隐含层神经元个数可设置为测井曲线个数的一半[23-25]。由于CRBM模型目的只是提取数据特征，所以只要提取的特征满足迭代条件即认为CRBM模型完成了任务，这使得该模型的调参工作也变得非常简单。图4展示了测井源数据和由CRBM模型得到的重构数据的对比情况。可见，各曲线的两种数据的吻合度非常高，表明CRBM模型对源数据的提取是有效的。在完成CRBM模型处理后，分别利用原始学习样本和提取特征数据对PSO-XGBoost混合模型进行训练。图5显示了PSO模型作用在XGBoost模型上的优化过程。可以明显地看出，PSO模型能够有效地优化XGBoost模型，尤其是在处理提取特征数据的情况下。在完成XGBoost，PSO-XGBoost和CRBM-PSO-XGBoost 3种模型的训练之后，预测目标便可进行处理，这里先以HA井为例。3种模型的预测准确率分别为51.00%，80.33%和92.67%，显示出提出模型的预测能力最强。图6以柱状图的形式展示了部分岩性预测结果。图中取心道的信息为实际取心柱的观察结果，已经通过深度校正归位。为便于分析，在取心道上选择了20个样点进行对比。通过观察发现，XGBoost模型结果中有10个错误样点(No.1，3，5，10，12，14，15，17，18，19)，PSO-XGBoost混合模型有6个(No.3，6，12，14，16，18)，而提出模型仅有2个(No.12和18)。由对比可知，XGBoost模型在使用经验参数的情况下得到的预测结果不能准确地反映岩性实际分布规律，而经CRBM模型和PSO模型优化后，其预测能力得到明显提升，得到的预测结果非常可靠，可有效地反映储层岩性分布情况。

在明确PSO模型和CRBM模型的嵌入对XGBoost模型的预测能力有提升作用之后，提出模型将与PNN和SVM模型进行对比。由于对比模型在建模时也需要用到经验参数，因此为使所有验证模型在预测时都能达到最佳状态，PSO模型和CRBM模型也将对PNN和SVM进行优化。表2记录了所有验证模型参数的设置及其优化结果。对于验证井HA，表3记录了用3种优化模型得到的预测结果。可见，在相同优化的条件下，XGBoost模型以92.67%的高识别准确率成为预测能力最强的模型。图7以柱状图的形式展示了HA井部分岩性预测结果。通过观察发现，CRBM-PSO-PNN模型预测结果有6个错误样点(No.2，6，9，14，16，18)，CRBM-PSO-SVM模型有4个错误样点(No.2，9，13，19)，与提出模型的2个错误样点相比，表中数据格式为(最小值，最大值)。

表1 验证模型参数设置及优化结果Table 1 Parameters selected for the validation model and corresponding optimized data

表2 CRBM参数设置Table 2 Parameters selected for the CRBM model

反映出PNN和SVM优化模型所给的预测结果不能准确地描述储层岩性分布状况。

分析HA井预测结果之后，再利用3种模型对HB井进行预测。建模时，PSO模型和CRBM模型所用的参数设置不变。表3给出了3种优化模型的预测结果。结果显示，混合模型CRBM-PSO-XGBoost的预测准确率仍为最高，达90.33%，再次表明提出模型的预测能力最强。

在实验2中，所有4 606个学习样本将用于建模，其目的是检验在训练更多学习样本的情况下，各验证模型的预测能力是否有所加强。建模时，PSO模型和CRBM模型所用的参数设置与实验1的一致。表3记录了用3种优化模型得到的两口验证井的预测结果。通过对比发现：①在训练更多学习样本后，各验证模型的预测准确率都有所提升，表明增大训练样本容量是提高模型预测能力的一种有效途径；②提出模型的识别准确率最高，都超过了90%，不仅显示出提出模型所得的预测结果可靠性高，还再次证明了该模型的预测性能最佳。

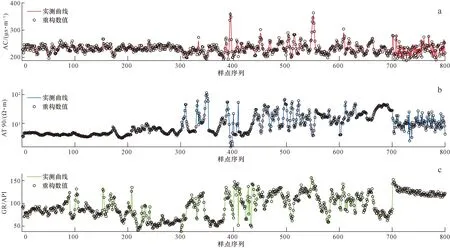
图4 CRBM重构数据检测Fig.4 Testing of reconstructing data for the CRBM modela. AC实测曲线与其重构数据比较；b. AT 90实测曲线与其重构数据比较；c. GR实测曲线与其重构数据比较

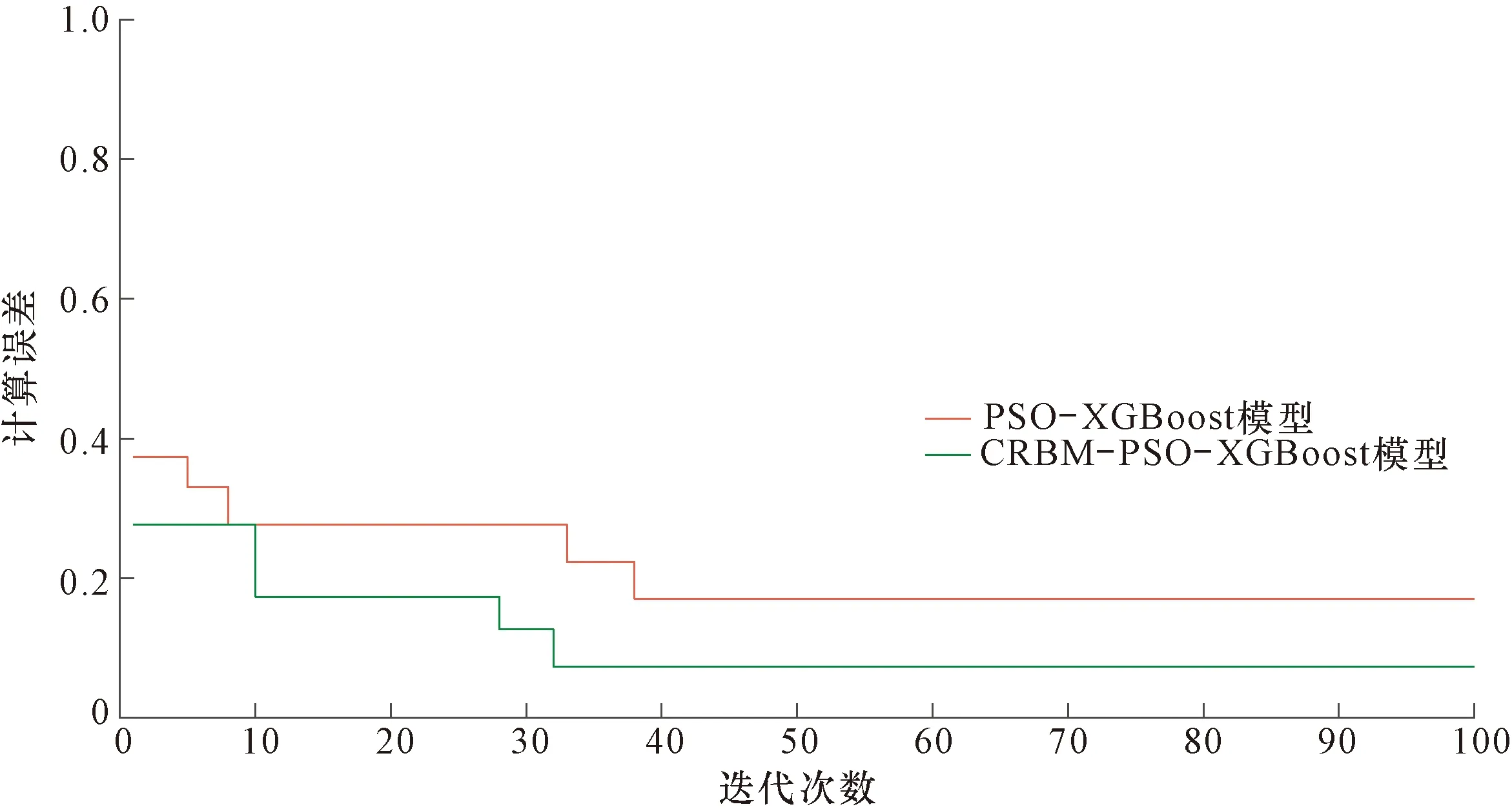
图5 PSO-XGBoost和基于CRBM的PSO-XGBoost训练优化过程Fig.5 Training optimization of PSO-XGBoost and CRBM-based PSO-XGBoost

表3中的计算时间数据显示CRBM-PSO-PNN耗时最长，而CRBM-PSO-SVM的最短。对于PNN模型，由于每个预测样本在预测时都要与全部训练样本进行计算，因此耗时最长，而且这种耗时会随着训练样本容量的扩大而急剧增加(对比实验1和实验2的数据)，表明在处理大数据时该模型效率低。SVM模型预测时，采用的是支持向量而不是全部学习样本，所以耗时短。但与XGBoost模型相比，SVM模型在两个实验中的计算时间也都仅快10 s左右，这在岩性识别问题中优先考虑预测准确率的情况下，并没有显示出该模型的预测效率高，反而体现了XGBoost模型的预测效率高。因此，综合来看，提出模型的预测效率最高，即使是在增大训练样本容量的条件下。