Geometry of time-dependent PT-symmetric quantum mechanics∗

Da-Jian Zhang(张大剑) Qing-hai Wang(王清海) and Jiangbin Gong(龚江滨)

1Department of Physics,Shandong University,Jinan 250100,China

2 Department of Physics,National University of Singapore,117551,Singapore

Keywords: time-dependent PT-symmetric quantum mechanics, geometry, time-varying inner product, unconventional geometric phase

1. Introduction

Standard quantum mechanics is built upon a fixed Hilbert space,with the associated inner product of two complex vectors being defined by the Dirac bra-ket notation. However,such a quantum theory may not consistently treat physical problems with time-varying Hilbert spaces. For example, it is not obvious how to depict the dynamics of a particle in an infinitely deep square-well potential with a moving boundary,of which the instantaneous Hilbert space changes with time.It is thus necessary and motivating to formulate new types of quantum theories that allow the inner product to change along a parameter path.

Inspired by the pioneering work of Bender and Boettcher concerning time-independent parity-time-reversal-symmetric(PT-symmetric)quantum mechanics(PTQM),[1]Gong and Wang proposed a Schr¨odinger-like equation capable of explicitly accounting for a time-varying inner product.[2]Such a proposal was further enriched and developed into a conceptual framework applicable to generic non-Hermitian systems,[3]in which a series of notions like the time-dependent Hilbert space,the observable,and the measurement postulate are formulated. These results lead to a consistent quantum theory extending the time-independentPTQM into the time-dependent domain,referred to as time-dependentPTQM hereafter.

The advent of time-dependentPTQM has spurred a renewed interest in the fundamentals of quantum mechanics.[4–10]In particular, how to construct the timevarying inner product was demonstrated in Refs.[5,6]and how to define the energy observable for a time-dependent Hilbert space was discussed in Refs.[3,9]. Further developments are witnessed by the reexaminations of some interesting issues in statistics mechanics,[11–15]such as the Jarzynski equality[11,13]and the Crooks fluctuation theorem.[3,12]

In this work,we explore the geometrical aspects of timedependentPTQM, which is a fascinating topic for the following reasons. First,given the fact that a time-varying inner product is always excluded in standard quantum mechanics,its nontrivial interplay with other concepts in quantum physics,e.g., the Berry phase,[16]is still not well understood in a unified fashion. Second,even in the absence of a time-varying inner product, geometric aspects of standard quantum mechanics are known to be of profound importance in various frontier topics of quantum information science and condensed-matter physics. One thus anticipates that physics arising from a timevarying inner product shall advance our fundamental understanding of the profound role of geometry in time-dependentPTQM. Last but not least, there have been ongoing investigations of physical properties, especially topological properties,ofPT-symmetric systems recently.[17–38]In view of this,a systematic inspection of the geometry of time-dependentPTQM would be a useful, perhaps indispensible, reference point to tackle physical problems involving time-varying system’s parameters.

The purpose of this work is to present comprehensive and rigorous results regarding the geometry of time-dependentPTQM. To this end, we start with the identification of a geometric phase(GP)that emerges naturally from a cyclic evolution of aPT-symmetric system. Then,with the motivation of revealing the geometry underlying the GP,we formulate,in succession,a series of related differential-geometry concepts,including connection,curvature,parallel transport,metric tensor, and quantum geometric tensor. Of particular interest is the metric tensor advocated here, which may be Riemannian or pseudo-Riemannian,depending on the physical context under consideration. Its pseudo-Riemannian feature is absent in standard quantum mechanics. As detailed below,the findings of this work are applicable to a rather general physical context and include the results of Refs.[4,10]as special cases.

To exemplify the application of our findings, we revisit one well-known example displaying the so-called unconventional GP,[39]which is the sum of a GP and a dynamical phase(DP)proportional to the GP,and as such,may not be well understood within the geometric theory in standard quantum mechanics. Here,we show that the unconventional GP,instead of being the sum of a GP and a DP, can be expressed as a single GP found in this paper, with the associated metric tensor categorized as a pseudo-Riemannian metric. This provides an interesting interpretation of the geometric nature of the unconventional GP.

This paper is organized as follows. In Section 2, we recapitulate some fundamentals ofPTQM. In Section 3, we identify the GP. In Section 4, we formulate a series of differential geometry concepts, including connection, curvature,parallel transport, metric tensor, and quantum geometric tensor.Section 5 presents our interpretation of the unconventional GP.Section 6 provides a general formula for GP which unifies several real and gauge-invariant GPs in the literature,and Section 7 concludes this work.

2. Fundamentals of PT QM

To present our findings clearly,we recapitulate some notions in time-dependentPTQM,[2,3]such as the metric operator, the physical Hilbert space, the physical observable, the Schr¨odinger-like equation,and the density operator.

A positive-definite operatorWis said to be the metric operator for aPT-symmetric systemSwith unbrokenPTsymmetry if it satisfies

whereHdenotes the Hamiltonian of the systemS. Usually,Hdepends on some system’s parametersλ:=(λ1,...,λm),which belong to a parameter manifoldM[m=dim(M)]representing the classical configuration of control fields. In the following,we denote the metric operator and the Hamiltonian byW(λ)andH(λ),respectively,in order to indicate their dependence on the parametersλ.

The physical Hilbert space ofS,denoted asℋ(λ),is defined to be the Hilbert space endowed with the following inner product:

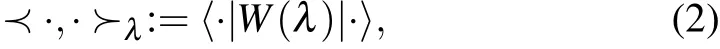
which is dependent onλ. It is worth noting that two states|ψ〉∈ℋ(λ)and|φ〉∈ℋ(λ′)are not comparable whenλ/=λ′,as they belong to two different physical Hilbert spaces.

An operatorOis said to be a physical observable ofSif it is a Hermitian operator under the new inner product in Eq.(2),

or equivalently,

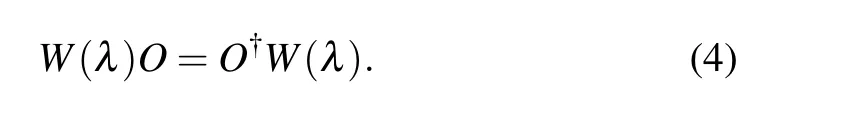
Apparently,H(λ)is a physical observable. It has been argued thatH(λ)can be regarded as the energy observable ofS.[3,9]

An evolution ofSis associated with a parameter pathλt ∈Mover a time interval[0,τ]. For this,the physical Hilbert space moves with time,and the evolving state|ψ(t)〉at timetbelongs toℋ(λt).The Schr¨odinger-like equation guaranteeing the unitarity of the evolution is found to be(¯h=1)[2]

For a state|ψ〉∈N(λ), the associated density operatorρis defined to be[3,10]

It is easy to see thatρis a positive operator with respect to the inner product (2) and satisfies tr(ρ)=1 andρ2=ρ; that is,it fulfills the conditions of being a density operator for a pure state. Similar to the two states|ψ〉∈N(λ)and|φ〉∈N(λ′),their associated density operatorsρ=|ψ〉〈ψ|W(λ) andσ=|φ〉〈φ|W(λ′)can be regarded as identical if and only ifλ=λ′and|ψ〉= eiϑ|φ〉for someϑ ∈R.

3. Geometric phase

Let us consider the situation that the evolving state|ψ(t)〉ofSreturns to its initial physical state,|ψ(τ)〉= eiα|ψ(0)〉,and moreover, the system’s parameters return to their initial values,λτ=λ0. This defines a curve of density operators

Equation(14)indicates that the phaseβdepends explicitly on the Hamiltonian and thus represents a DP.On the contrary,the phaseγ,as a factor obtained by removing the DP from the total phase, depends solely upon the closed curveCin Eq. (9),as will be proved shortly. Therefore,γis our GP.It is interesting to note that DP and GP for non-Hermitian systems were usually defined to be complex in the previous works(see,e.g.,Refs.[40,41]). By contrast,both the DP and GP defined here are real phase factors. Indeed, sinceH(t) is a physical observable satisfying Eq. (3), the term≺φa(t),H(t)φa(t)≻λtappearing in Eq. (14) is real, which leads to the fact thatβis real. The fact thatγis real follows immediately from the operation of taking the imaginary part of a complex number in Eq.(15).

To prove thatγis uniquely determined byC,we resort to the following gauge-invariant formula ofγ:

Here,the term e∫t0dsRe≺φb(s),˙φb(s)≻λshas been neglected,since it is a real and positive number and thus makes no contribution.Equation(22)clearly shows thatγis uniquely determined byC.

It is worth noting that the result just presented includes the results of Refs.[4,10]as special cases. Indeed,the GP obtained in Refs.[4,10]is for the eigenstate ofH(λ),and therefore,is a counterpart of Berry’s phase.[16]In contrast,the GPγobtained here is for a generic cyclic state which may or may not be the eigenstate ofH(λ). In this sence,γis a counterpart of Aharonov–Anandan’s phase.[42]Moreover,it has been shown[3]that the dynamics of a generic non-Hermitian system can be described by the Schr¨odinger-like equation (5)with Eq. (6). This implies that the GP found here is applicable to a much more general physical context compared with Refs.[4,10].

4. Differential geometry concepts

There is a one–one correspondence between rays inR(λ)and density operators overℋ(λ). Indeed, given a ray [|ψ〉]inR(λ), one can assign to it a unique density operatorρoverℋ(λ), which isρ=|ψ〉〈ψ|/≺ψ,ψ ≻λ. Conversely,given a density operatorρoverℋ(λ), one can express it asρ=|ψ〉〈ψ| for some|ψ〉∈N(λ). Then, the unique ray associated toρis[|ψ〉]. Under the effect of this one–one correspondence,a curve inRcan be simply understood as a curve of density operators. Now,it becomes clear thatCin Eq.(9)is actually a curve in the space of raysR.

A coordinate system can be established by considering a local patch onRand the region ofP(R,U(1)) over the patch. Let (λ1,...,λm,λm+1,...,λm+n) be the local coordinates of a point ofRon the patch. Here,λµ,µ=1,...,m,are the system’s parameters as before, used to specify which subset,R(λ), the point belongs to. The remainderλµ,µ=m+1,...,m+n, are used to represent local coordinates parameterizing the manifoldR(λ) [n= dim(R(λ))]. Then,the local coordinates of a point ofP(R,U(1)) can be expressed as (θ,λ1,...,λm,λm+1,...,λm+n), whereθ ∈R is defined up to an integer multiple of 2π.[43]Using these local coordinates, we can express density operators and states in a coordinate-dependent form. Since a density operatorρis a point ofR, it can be represented asρ=ρ(λ1,...,λm+n).Likewise,a state|φ〉,as a point ofP(R,U(1)),can be written as|φ〉=|φ(θ,λ1,...,λm+n)〉.

With these notions, we may now start to formulate differential geometry concepts, including connection, curvature,parallel transport, metric tensor, and quantum geometric tensor.

4.1. Connection

Equation(23)implies that the horizontal part satisfies

4.2. Curvature

4.3. Parallel transport

A choice of connection is equivalent to a notion of parallel transport. By definition,a curve|φ(t)〉is said to be parallel transported along a curve in the base manifold if the vertical part of its tangent vector,i.e.,|˙φv(t)〉,vanishes. Using Eq.(23)and noting the relation|˙φ(t)〉=|˙φv(t)〉+|˙φh(t)〉,we have

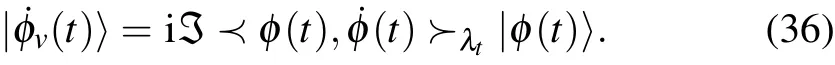
Therefore,|˙φv(t)〉vanishes if and only if

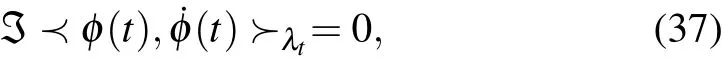
representing the parallel transport condition associated with the connectionA. Equation (37) is a counterpart of the Berry–Simon parallel transport condition.[44]It depicts a parallel way of transporting|φ(t)〉along a curve inR. Evidently,|φb(t)〉fulfills Eq. (37) and hence is parallel transported. This transport is along the closed curveCin Eq. (9),since|φb(t)〉〈φb(t)|=ρ(t). Starting at an initial point|φb(0)〉,the transport will end at a different point|φb(τ)〉= eiγ|φb(0)〉,as can be easily verified by using Eq. (18). The difference,known as holonomy,is precisely our GPγ.

4.4. Metric tensor

To obtain a metric tensor, we resort to the formula for the fidelity between two nearby density operatorsρ(λ1,...,λm+n) andρ(λ1+δλ1,...,λm+n+δλm+n).[10]It reads

4.5. Quantum geometric tensor

This point can be easily verified by comparing Eq. (42) with Eq.(43).

From Eqs.(45)and(46), it follows immediately that the quantum geometric tensor (43) depicts a unified picture: Its imaginary part gives the Berry curvature(35)and thus further determines the GP(31),whereas its real part induces the metric tensor(42)and thereby further determines the fidelity(39).

5. On the unconventional geometric phase

So far,we have presented our main findings,consisting of a GP and a series of differential geometry concepts, namely,connection, curvature, parallel transport, metric tensor, and quantum geometric tensor.To exemplify the application of our findings,we revisit one well-known example that yields an interesting GP,called the unconventional GP in the literature.[39]

The physical model studied in Ref.[39]is a harmonic oscillator. Its Hamiltonian reads

and|z〉denotes a coherent state. At the timet=τ:=2π/δ,the evolving state|ϕ(t)〉returns to its initial physical state,i.e.,|ϕ(τ)〉= eiγ(τ)|0〉, and it acquires a total phaseγ(τ). A remarkable observation made in Ref. [39] is thatγ(τ) has a nonzero DP component but is still of geometric nature, i.e.,it is an unconventional GP. In showing this, the DP and GP components ofγ(τ), denoted respectively byγdandγg, were calculated, and found to satisfyγd=ηγg(η/=0,−1). So,γ(τ)=(1+η)γg, indicating thatγ(τ) is of geometric nature as it inherits geometric features fromγg. Despite this interesting observation, it remains an open question whether the unconventional GP itself admits a geometric interpretation or not.

Physically speaking,thePT-symmetric system and its equivalent Hermitian system may be considered two different interpretations of the dynamics of a same physical system.

Suppose now thatz1(t) = iΩD(e−iδt −1)eiφL/δ, i.e.,z1(t)=z(t). For this, Eq. (52) reduces to Eq. (47). Hence,the evolution of the Hermitian system is simply the evolution process studied in Ref. [39]. As another interpretation of the dynamics of the same physical system, thePT-symmetric system undergos the corresponding evolution|ψ(t)〉= e−2z1(t)a†|ϕ(t)〉. Sincez1(τ)=z1(0)=0 and|ϕ(τ)〉= eiγ(τ)|ϕ(0)〉,this evolution is cyclic,and the evolving state|ψ(t)〉of thePT-symmetric system acquires the same total phaseγ(τ) as that of the Hermitian system. Note that for thePT-symmetric system, the total phase accumulated in any cyclic evolution is simply the GPγin Eq.(15),due to the vanishing of its Hamiltonian. Hence,γ(τ)=γ,i.e.,the unconventional GP is precisely the GP expressed by Eq.(15).

To shed more light on the unconventional GP, we calculate the quantum geometric tensor in Eq. (43), with which,we further obtain the curvatureΩand the metric ds2. To do this, we find the evolution operator of thePT-symmetric system. Using magnus expansion[47]and noting that the commutator ofK(t) at different time is a number, we have that the evolution operator reads e−2z1(t)a†D(z1(t)), up to a global phase factor,whereD(z1):= ez1a†−z1∗ais the displacement operator. So, starting at an arbitrary coherent state|“some complex number”〉, the evolving state|ψ(t)〉reads|ψ(t)〉= e−2z1(t)a†|z1(t)+“some complex number”〉, up to a phase factor. So,the evolving state is of the form e−2z1a†|z2〉,wherez2=z1(t)+“some complex number”. Substituting e−2z1a†|z2〉into Eq.(43),i.e.,setting|φ〉and|φ〉appearing in Eq.(43)as|φ〉= e−2z1a†|z2〉and|φ〉= e2z1∗a|z2〉,we obtain,after tedious but straightforward calculations,

That is,

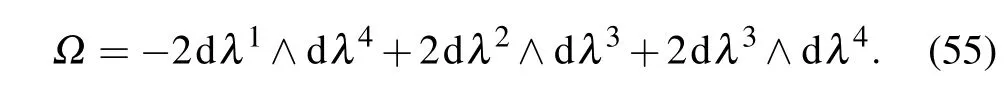
For the evolution process studied in Ref.[39],in which the initial state is|0〉,we havez1(t)=z2(t),leading to the constraintsλ1=λ3andλ2=λ4. Substitutingλ1=λ3andλ2=λ4into Eq.(55), we haveΩ=−2dλ1∧dλ2. From Eq. (45), it follows that

6. A general geometric phase

It may be an interesting topic for future work to generalize the GP found here to a more general setting,[48]like the non-cyclic case considered in Ref. [49]. This is a non-trivial problem, as the Hilbert spaceℋ(t) changes with timetin general.[3]To shed some light on the problem,we provide one possible way to achieve the generalization,

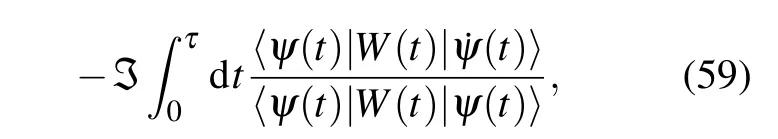
where|ψ(t)〉is an (unnormalized) state inℋ(t) andW(t) is the(time-dependent)metric operator associated withℋ(t).[3]Mathematically, the GP is defined as a functional of a state and the metric operator,γ=γ[ψ(t),W(t)]. It is easy to see thatγdefined in Eq. (59) is gauge-invariant and reduces to the GP given by Eq. (15) in cyclic cases. With the choice of Dirac inner-product, i.e.,W(t)=1, Eq. (59) reproduces AA phase for the cyclic states in Ref.[48]and non-cyclic states in Ref. [50]. Thus, the GP defined in Eq. (59) unifies real and gauge-invariant geometric phases in non-Hermitian systems.

7. Conclusion

We have presented a series of results on the geometry of time-dependentPTQM.Specifically,they are the GP(15),the connection(28),the curvature(35),the parallel transport condition(37),the metric tensor(42),and the quantum geometric tensor(43). The GP emerges naturally from cyclic evolutions ofPT-symmetric systems,and it may be regarded as a counterpart of Aharonov–Anandan’s phase. The connection and curvature are responsible for the appearance of the GP,as expressed by Eqs.(30)and(31). The quantum geometric tensor is a unifying concept, of which the imaginary part gives the curvature and the real part induces the metric tensor, as described by Eqs.(45)and(46),respectively.

These results constitute a useful, perhaps indispensible,tool to tackle geometric problems involvingPT-symmetric systems with time-varying system’s parameters. As an illustration of their usefulness, we have solved the open question whether the unconventional GP admits a geometric interpretation or not. Specifically,we have shown that the unconventional GP,instead of being the sum of a DP and a GP,can be expressed as the single GP in Eq. (15), thus making its geometric nature undoubtedly clear.

Of particular interest is the finding that the metric tensor(42)may be pseudo-Riemannian,which is elusive in standard quantum mechanics. This leads to the intriguing fact that there can exist three types of evolutions for aPT-symmetric system, i.e., spacelike, lightlike, and timelike evolutions, as shown in the example involving the unconventional GP. Further studies on the implications/applications of the pseudo-Riemannian feature are highly desirable.