Variation of electron density in spectral broadening process in solid thin plates at 400 nm∗

Si-Yuan Xu(许思源) Yi-Tan Gao(高亦谈) Xiao-Xian Zhu(朱孝先)Kun Zhao(赵昆) Jiang-Feng Zhu(朱江峰) and Zhi-Yi Wei(魏志义)

1School of Physics and Optoelectronic Engineering,Xidian University,Xi’an 710071,China

2Beijing National Laboratory for Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

3University of Chinese Academy of Sciences,Beijing 100049,China

4Songshan Lake Material Laboratory,Dongguan 523808,China

Keywords: nonlinear spectral broadening,time-dependent nonlinear Schr¨odinger equation,self-phase modulation,electron density

1. Introduction

Supercontinuum generation is a key to the production of ultrashort femtosecond (1 fs=10−15s) laser pulses.Nowadays, a state-of-the-art titanium-sapphire (Ti:sapphire)chirped-pulse amplifier delivers pulses as short as 13 fs at an 800-nm central wavelength, which still contains almost 5 cycles.[1]The mainstream technique of few-cycle pulse generation is to compress multi-cycle pulses from laser amplifiers with inert-gas-filled hollow-core fibers[2,3]or multiple solid thin plates,[4,5]which broaden the spectrum of the input pulses by self-phase modulation (SPM),[6]and self-steepening.[7]Spectra of more than one octave have been obtained experimentally using hollow-core fibers and multiple thin plates,and utilized to stabilize the carrier-envelope phase (CEP) of the pulses.[8]Few-cycle laser pulses with CEP stabilized are an ideal driver for producing isolated attosecond(1 as=10−18s)pulses through high-order harmonic generation(HHG)in the extreme ultraviolet (XUV) band,[9,10]which is an excellent tool for studying dynamics in atoms and molecules with attosecond time resolution.[11]In HHG, driving pulses with shorter wavelengths have the potential to improve the efficiency and obtain high-flux high-order harmonics and attosecond pulses.[12]

Femtosecond pulses at 400 nm with a broad spectrum are usually generated by two methods. The first method is to directly double the frequency of a broadband 800-nm pulse,but the output beam in such a scheme carries angular dispersion and broadband frequency doubling is usually challenging and inefficient. The second method is to produce a relatively narrow-band 400-nm femtosecond pulse followed by spectral broadening to produce the desired broad spectrum at 400 nm.Supercontinuum generation by a hollow-core fiber is a very mature technic, while in recent years many groups have used multiple solid thin plates to broaden the spectrum at different wavelengths. Pulses shorter than 10 fs have been obtained at 400 nm,with a spectrum covering 365 nm to 425 nm at−20-dB intensity level.[13,14]To this end, we investigate the generation of continuous spectrum centered at 400 nm from solid thin plates experimentally and numerically. We calculate the change of electron density in the medium to confirm the occurrence of the self-focusing process,and prove our experimental process safely below the documented avalanche plasma density.

2. Simulation model

Here, we use the three-dimensional (3D) propagation equation to simulate femtosecond laser pulses at 400 nm to be spectrally broadened by multiple thin plates. The propagation equation is a generalized time-dependent Schr¨odinger equation(TDSE)[15–18]

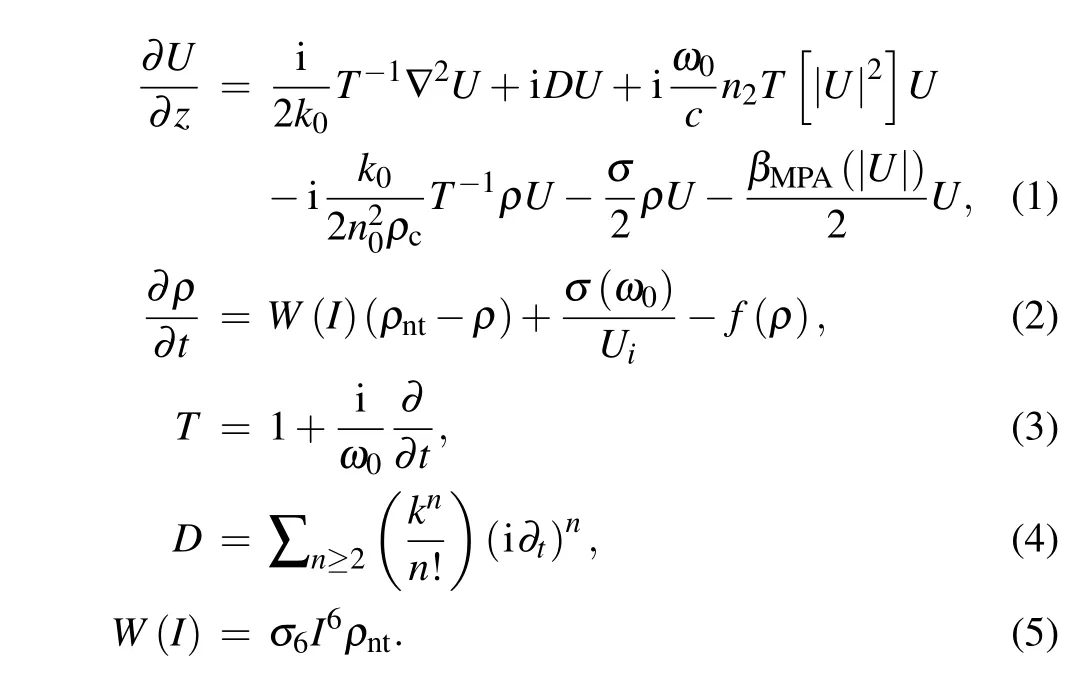
Here,zis the propagation variable,tis the retarded time,andUis the linearly-polarized electric field in the form of[15]

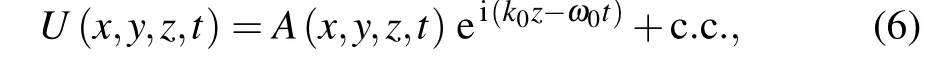
withω0being the angular frequency of the carrier wave,k0the wave vector,andcthe speed of light in vacuum,I=|U|2is the intensity of the optical field,Tis an approximated differential time operator, as given in Eq. (3), which plays an important role in self-steepening and spatiotemporal coupling.The first term of Eq. (1) is for diffraction. The operator ∇describes the spatial change of the pulse during propagation.The second term is for dispersion, andDis an operator accounting for dispersions as shown in Eq. (4), whereknis the corresponding dispersion coefficient. The third term refers to the Kerr focusing effect,containing self-phase modulation and self-steepening. Here we have omitted the Raman-delayed nonlinear response, because the pulse width in our simulation is shorter than the Raman-delayed nonlinear response time which is on the order of hundreds of femtoseconds.[15]The fourth term incarnates the nonlinearity caused by ionization, whereρis the ionized electron density in the medium,ρcthe critical plasma density, and the initial density of SiO2molecules in fused silicaρnt=2.1×1019mm−3.[16]The fifth term reflects the impact ionization, and the collision crosssectionσis corresponding to a central frequencyω0. The last term represents the multiphoton absorption.

Solving the generalized nonlinear Schr¨odinger equation is an effective analytical method of solving the problem of pulse propagation in the medium. However, the quantity of data and time for 3D calculation are extremely large when the spatial variation, dispersion, and nonlinear terms of the pulse are calculated at the same time.We employ the split-step Fourier algorithm and calculate the linear(diffraction and dispersion) and nonlinear (Kerr nonlinearity and plasma effect)terms separately.

The basic principle of the application of the split-step Fourier transform method in nonlinear propagation equations is to convert high-order partial differential terms into frequency domain and momentum domain through Fourier transform to reduce the quantity of calculations. After the calculation is completed,the result is converted back into the spacetime domain by the inverse Fourier transform to perform operations on the remaining regular terms or low-order partial differential terms. The split-step Fourier algorithm calculates the propagation of the pulse in the medium in sections. In each segment, cyclically execution provides all the information about the final time domain of the pulse. In particular,in the calculation,we converted the terms containing high-order partial differentials such as the diffraction term and the dispersion term into the frequency domain and momentum domain for calculation, while other nonlinear terms are placed in the space-time term for calculation.

Because the required nonlinear Schr¨odinger equation includes high-order partial differential calculations,and the nonlinear term is coupled with the parameters in pulse time domain,the propagation equation cannot be solved analytically,but it can do numerically. The split-step Fourier method has the advantages of fast calculation speed and high precision when solving this kind of problem. The disadvantage is that this method still requires significant computing power. If we consider higher-order nonlinear processes, we need to add more terms, which brings more difficulties to the calculation process.

In this study, we ignore the response of the air, and only calculate the pulse propagation in the solid material,because outside the solid plates the spectral width is practically unchanged.[17]The ionization rateW(I) for silica is taken from Keldysh’s multiphoton rate[16]as described in Eq. (5). Fused silica, with which spectral broadening has been observed in experiment, is chosen as the medium in this study. The nonlinear refractive indexn2for fused silica is 2.52×10−16cm2/W at 800 nm and 2.49×10−16cm2/W at 400 nm.[19]The ionization potentialUiis 9 eV for fused silica,[16]the avalanche cross-sectionσis 6×10−18cm2,and the recombination timeτrecis 27 fs.[15]

The input pulse is at a center wavelength of 400 nm,and we use 100-µm-thick fused silica plates. The initial pulse energy is taken to be 125 µJ. In the calculation, the initial pulse envelope is the envelope after second harmonic generation(SHG),measured by transient grating frequency-resolved optical gating[20](TG-FROG)setup in the experiment.

3. Experiment

In the experiment, pulses of 5 mJ at 1 kHz, 790 nm were emitted from a Ti:sapphire laser system. The transformlimited pulse width was 35 fs but the pulse was actually measured to be 53 fs,which is due to the residual high-order chirp out of the laser compressor. The experimental setup is illustrated in Fig.1.A portion of 600µJ of the output pulse was reflected into the experiment by a beam splitter.A telescope was employed to shrink the beam diameter, which was composed of two lenses, a plano-convex lens withf=300 mm and a plano-concave one withf=−100 mm. The distance between the two lenses was 200 mm. After the telescope, a 140-µmthick barium borate crystal (BBO) was used to generate the second harmonic. The BBO was cut for type-I (o+o→e)phase matching(θ=29.2°,ϕ=0°). The polarization of second harmonic was changed by type-I phase matching in BBO,fromptos. The second harmonic pulses of 145µJ at a center wavelength of 395 nm were obtained after BBO, with a beam radius of 2.5 mm. A set of climbing mirrors were used to change the polarization back top. One of the climbing mirrors was dichroic with high reflectance at 400 nm and high transmission at 800 nm.One pair of chirped mirrors were used to compress the second harmonic pulses to 64 fs with 125µJ,characterized by a homemade TG-FROG setup,[21]and the results are shown in Fig.2.

Fig.1. Experimental setup for 400-nm continuum generation.

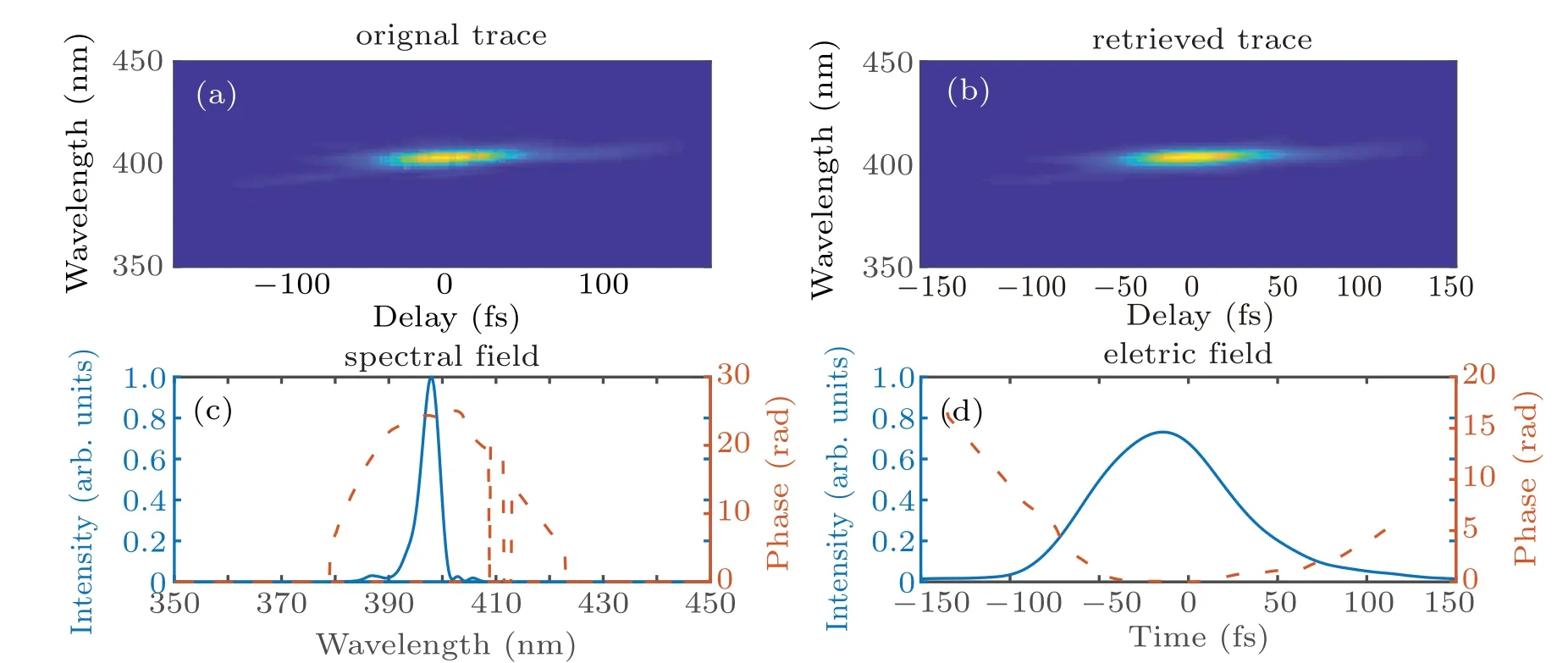
Fig. 2. TG-FROG measurements of the second harmonic pulses, showing (a) measured FROG trace, (b) retrieved FROG trace, (c) retrieved spectral intensity(solid)and phase(dashed),and(d)normalized temporal intensity(solid)and phase(dashed)of the pulse.

Fig.3.Spectrum of input second harmonic generation(SHG)pulse(dashed)and continuum(solid)after spectral broadening.

A 500-mm lens was used to focus the second harmonic beam into a 120-µm spot at the focus, where the peak intensity was 6.7×1012W/cm2. The beam propagated through six thin fused silica plates each with a thickness of 100 µm,placed near the focus. The first plate was 15 cm in front of the focus, the distances from the plate in front for the remaining five plates were 8 cm,2 cm,2 cm,2 cm,and 1.5 cm,respectively. The plates were placed at the Brewster’s angle(55.8°)to reduce loss. The beam out of the thin plates was collimated by anf=800 mm aluminium concave mirror. At this point,a 95-µJ continuum, covering 370 nm to 430 nm at−20-dB intensity level,was achieved and the results are shown in Fig.3.After two pairs of chirped mirrors,the pulse energy was 78µJ.The spectrally broadened and compressed pulse was measured with TG-FROG, and the width of the main peak in the pulse envelop was 40 fs,the results are show in Fig.4.

4. Results and discussion

It is clear from Fig. 4(c) that the spectrally broadened pulse has a complex high-order chirp, resulting in a threepeak envelope. The slope of the phase curve around 390 nm is positive and the slope around 415 nm is negative. In the time domain, two satellite pulses appear on both sides of the center peak. As shown in Fig. 2(c), the phase of the incident pulse also has the same shape, and there are two satellite pulses in front and in back of the main peak,respectively.The two satellite pulses of the incident pulse have low intensity much weaker than the central peak. Therefore, the highorder chirp of the spectrally broadened pulse as measured by TG-FROG(Fig.4),is most likely carried over from the input pulse(Fig.2).

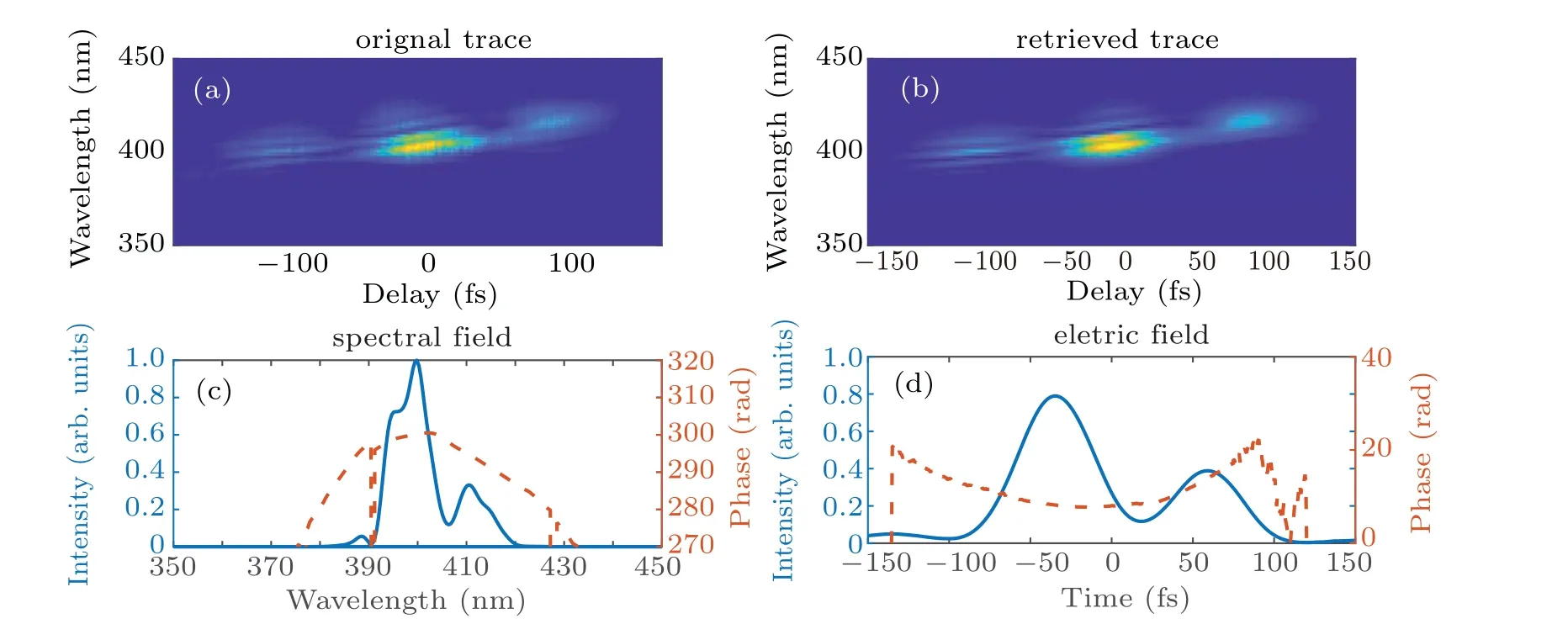
Fig. 4. TG-FROG measurements of spectrally broadened pulse: (a) measured FROG trace, (b) retrieved FROG trace, (c) retrieved spectral intensity(solid)and phase(dashed),(d)normalized temporal intensity(solid)and phase(dashed)of pulse.

We use the 3D propagation equation (Eq. (1)) to simulate the broadening results of the 400-nm pulses. In the simulation, the initial envelope takes the form of the input SHG pulse envelope directly measured by TG-FROG in the experiment(Fig.2). The simulation parameters are also the same as those in the experiment. Figure 5 shows good agreement between simulated result and experimental measurement.As observed in experimental result and simulation result, the spectral broadening of 400-nm pulses is not so pronounced as in the 800-nm experiment under similar experimental conditions, which is maily due to the fact that self-steepening is weak when the pulse is long. When a pulse of several hundred femtoseconds is broadened in fiber[22]or multipass cells(MPC),[23]only pure SPM and Raman effect take place, and the spectral lines are broadened symmetrically on both sides of the central wavelength,as obtained in the experiment.

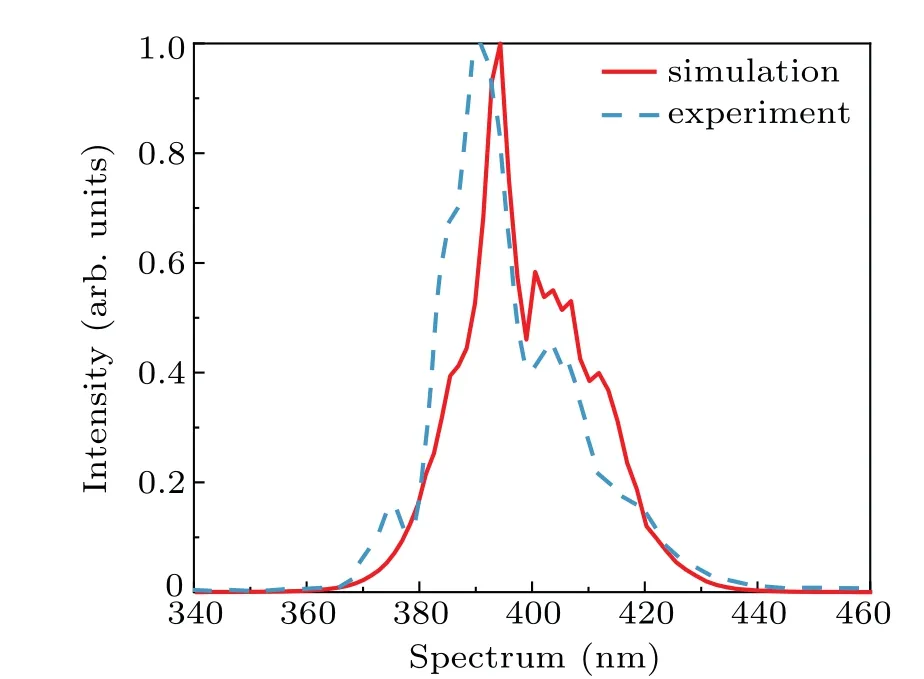
Fig.5. Experimental(dashed)and simulated(solid)broadened spectra.

In Eq. (1), the collision ionization and multiphoton ionization of the fifth and sixth terms reduce the pulse intensityI.Excessive ionization leads to pulse splitting and loss of spectral coherence. We place the fused silica away from the focus to avoid being excessively ionized,but not too far away from the focus to obtain as wide a spectrum as possible. In the experiment,when we move the fused silica along the optical axis close to the focus,the spectrum is broadened significantly but with a decrease of power. This shows that the ionization at the focus leads to strong broadening, resulting in a large loss of laser energy. At the same time, when we focus the laser directly in the air in the experiment,the spectrum broadening is negligible. This means that the spectrum broadening originates from the nonlinear effect in fused silica.

As indicated in Eq. (1), the SPM and self-steepening terms are proportional to intensityI,while the ionization termW(I) is proportional toI6. Therefore, the ionization process(thus free electron density in the medium)is more sensitive to the intensity variation than the SPM and self-steepening. The self-focusing threshold is 0.6 MW in fused silica at 400 nm.[24]Under our experimental condition,self-focusing takes place in each piece of silica. In the simulation,we calculate the change of electron density as the beam propagates through each piece of fused silica. Self-focusing leads the beam size to decrease and the beam intensity to increase in the fused silica plates so that the free electron density increases correspondingly.

The simulation result shows that the electron density in the second to fifth pieces of silica increases significantly with the beam propagation, which is provoked by self-focusing as shown in Fig.6. As the 400-nm pulse propagates through the silica plates,self-focusing takes place whenever the beam enters into the plate,therefore the spectrum is broadened. However,the focus of the self-focusing is formed outside the fused silica, and as the beam propagates through the focus into the divergence mode,it enters the next fused silica plate,where the same process is repeated. Until the peak power density of the beam becomes insufficient to produce further spectral broadening,at this point the process is over. This phenomenon has been discussed from the experimental point of view in previous study,[17]and now we confirm it with numerical simulation.

The result also show that the electron density reaches a maximum value in the fourth piece of fused silica(Fig.6),this is consistent with the fact that the fourth piece is placed closest to the beam focus and the laser intensity reaches the maximum value in the thin plates. The maximum electron density is calculated to be 5×1015mm−3,where the density of SiO2molecules in fused silica is 2.1×1019mm−3, and the electron density is safely below the documented avalanche plasma density of 2.1×1017mm−3.[17,25]In the experiments,ionization does not produce visible filaments in the thin plates in the broadening process.

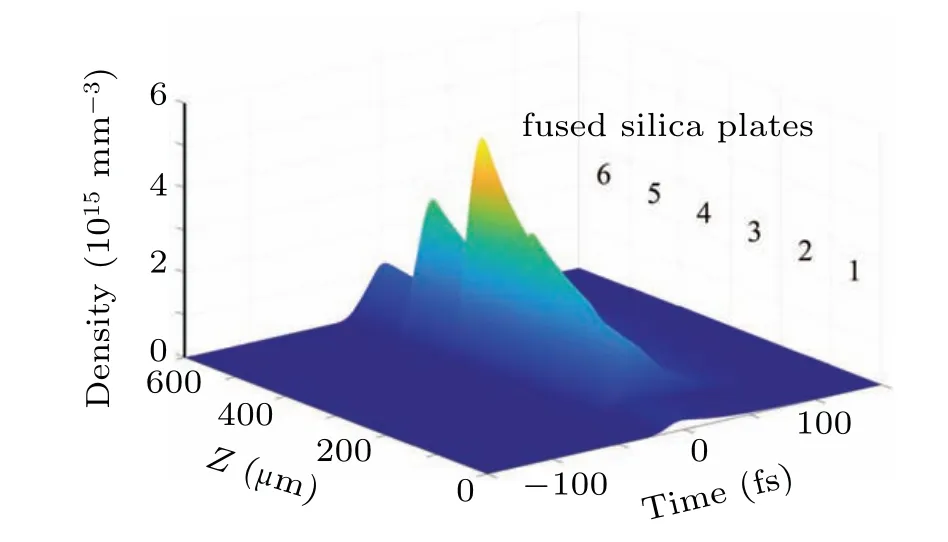
Fig.6. Electron density changes in each fused silica.

A large electron density and a large variation of the electron density during the propagation will affect the spectral phase and wavefront of the pulse significantly. In our simulation result,the electron density in the fused silica plates is at a low level, well below the avalanche plasma density, and its variation in each thin plate is also well within an order of magnitude or even less.At the same time,low electron density also results in the low loss of the laser energy and low modulation of the phase. This indicates that the spectral broadening observed after the beam has propagated through the fused silica plates is induced mostly by phase modulation caused by Kerr effect. It is important in spectral broadening experiments with multiple thin plates to minimize the ionization and plasma effect to avoid energy loss and unexpected phase variation.

5. Conclusions and perspectives

In summary, we achieve spectrum broadening of pulses with complex dispersion. We use 6 pieces of 100-µm-thick fused silica for spectrum broadening at 400-nm central wavelength,and obtain a spectrum covering a range from 365 nm to 445 nm.We employ a 3D propagation equation to simulate the spectrum broadening process in multiple solid thin plates.The numerical simulation results are in excellent agreement with the experimental observations. Our calculations reproduce the experimental process very well. We find experimentally that the strong self-focusing occurs in the silica plates in the spectrum broadening process, and we use the change of electron density to confirm this interesting process. The calculations conduce to clearly describing the whole spectrum broadening process in multiple thin plates. Finally,the calculation shows that the electron density in the broadening process is always safely below the documented avalanche plasma density, and confirms that the ionization or plasma effect does not play a major role in the spectral broadening process.

Acknowledgment

The authors are grateful to Prof. Chengyin Wu and Dr.Zhiming Miao for providing the laser beam and for their helpful discussion as well.