自适应广义全变差的图像泊松去噪算法
2021-10-28金正猛
王 洁,金正猛,冯 灿
1.南京邮电大学 理学院,南京 210023
2.北方信息控制研究院集团有限公司,南京 211153
图像在获取、传输过程中经常受到噪声干扰,特别在天文、医学、雷达等成像系统中不可避免地产生噪声。如何有效地去除图像中的噪声,同时突出感兴趣的区域和边缘纹理等重要特征信息,一直是图像处理中有挑战的课题之一。通过分析噪声和图像信号之间的关系,一般可将噪声分为加性噪声和乘性噪声。近二十年来,基于加性高斯噪声的去除方法被人们广泛研究。如:基于全变差(Total Variation,TV)正则化的ROF模型[1]及其扩展模型[2-3]。由于ROF模型在去噪的同时,能很好地保护图像的重要特征-边缘,使得该模型被人们广泛采纳。但是,利用ROF模型,去噪后的图像在平滑区域会不可避免地出现阶梯效应[4],且纹理等细节信息会丢失[5]。针对这些缺陷,基于高阶TV的图像去噪模型[6-7]陆续被提出。另一方面,在以光子探测为成像基础的医学和天文成像系统中,图像中经常出现泊松噪声。与加性高斯噪声不同,泊松噪声是与图像信号之间有很强的依赖性。对于泊松噪声的处理,有小波方法[8]、贝叶斯方法[9]、自适应窗方法[10]和变分方法[11]。
本文关注的是基于变分法的图像泊松去噪方法。2007年,Le等[11]结合TV正则化途径,采用最大后验估计的方法推导出了去除泊松噪声的变分模型(Le模型)。进一步,金正猛等[12]通过变分法推导出Le模型解的框式约束,提出了带框式约束的Le模型快速数值求解算法。2017年,Zhang等[13]应用广义交叉验证(Generalized Cross Validation,GCV)技术[14],提出了自适应的全变差泊松图像去噪算法。虽然这些方法能较好地去除图像中的泊松噪声,但由于这些方法都是基于TV正则化途径,使得去噪后的图像会出现阶梯效应。近年
来,广义全变差(Total Generalized Variation,TGV)正则化途径被人们应用于泊松图像去噪中[15-16]。Lv等[16]结合Le模型中的数据保真项,提出基于TGV正则化的泊松图像去噪模型(Lv模型)。实验结果表明,Lv模型在去除泊松噪声的同时,能有效地消除图像中的阶梯效应。
Lv模型同其他基于变分方法的图像去噪模型一样,也存在正则化参数选取的问题。特别在真实的泊松图像中,泊松噪声的统计水平未知,如何有效地选取正则化参数是数值求解Lv模型的一大难题。本文结合交替迭代极小化方法和广义交叉验证技术,提出该模型的参数自适应迭代算法。最后,数值实验结果验证了所提算法的有效性和可行性。
1 相关模型
在本文中,f表示观察到的图像,u表示原始的清晰图像,n是泊松噪声。一般认为泊松图像满足:
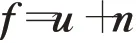
这里假定泊松概率为:

在文献[11]中,Le等结合TV正则化,通过最大后验估计(MAP)方法,推导出如下去除泊松噪声的变分模型:
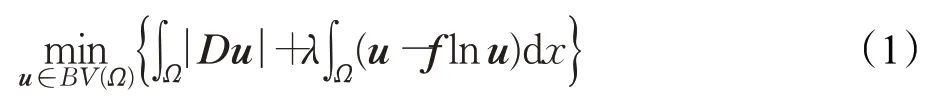
其中,λ>0为正则化系数,第一项为TV正则项,第二项为泊松数据保真项。后面称模型(1)为Le模型。在文献[12]中,作者通过变分方法,推导出Le模型解的一框式约束,并提出了带框式约束的Le模型快速数值求解算法。实验结果表明,该快速算法不仅能很好地去除图像中的泊松噪声,还大大提高了计算速度。注意到基于TV正则化的Le模型,去噪后的图像中会出现阶梯效应。为了消除阶梯效应,Lv等[16]提出了基于TGV正则化的泊松图像去噪模型(简称为Lv模型):
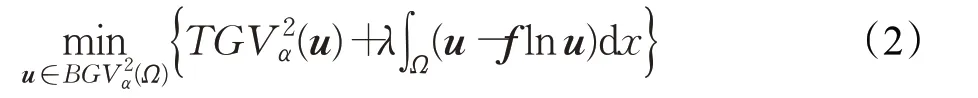


因此,文献[16]中对Lv模型(2)进行数值求解时,考虑该模型的如下等价形式:
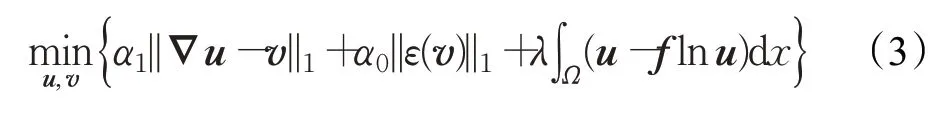
尽管Lv模型能较好地消除图像去噪中的阶梯效应,但与其他去噪模型一样,Lv模型也存在参数选择问题。特别地,当泊松图像中的噪声信息未知时,正则化参数的选取对去噪结果影响较大。为了解决这一问题,利用交替迭代极小化算法,设计该模型的自适应快速算法。在每步迭代求解过程中,结合广义交叉验证(GCV)方法,自动更新模型中的正则化参数。
2 交替极小化算法
通过简单的计算发现,模型(3)对于每个变量分别是严格凸的。因此,本文采用迭代极小化方法和算子分裂技巧[18]来数值求解优化问题(3)。在每步迭代过程中,结合GCV方法,通过求解关于某个参数变量的极小值问题来自动获取参数α1的值,从而达到自动更新模型中的其他参数。具体算法如下:
首先,引入辅助变量d和惩罚参数β,考虑求解问题(3)的逼近问题:

由经典的罚函数法[19]可知,当β取值充分大时,优化问题(4)的解趋近于原问题(3)的解。
然后,通过引入辅助变量w和z,则式(4)可等价转化为:
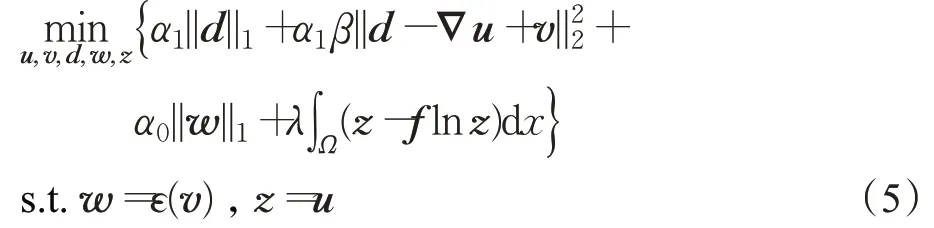
上式对应的增广拉格朗日函数为:
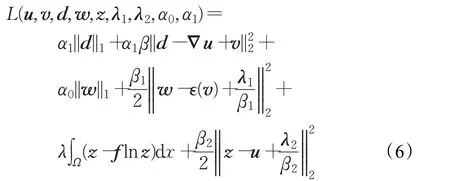
其中,β1、β2是惩罚参数,λ1、λ2是拉格朗日乘子向量。下面,通过交替迭代极小化方法,将鞍点问题(6)分解为如下几个子问题来交替求解。
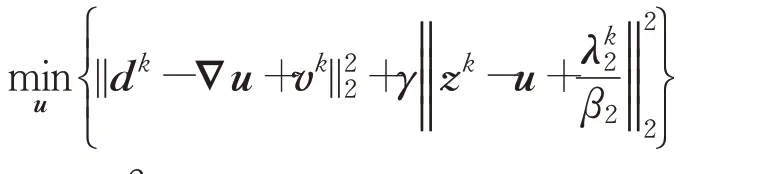
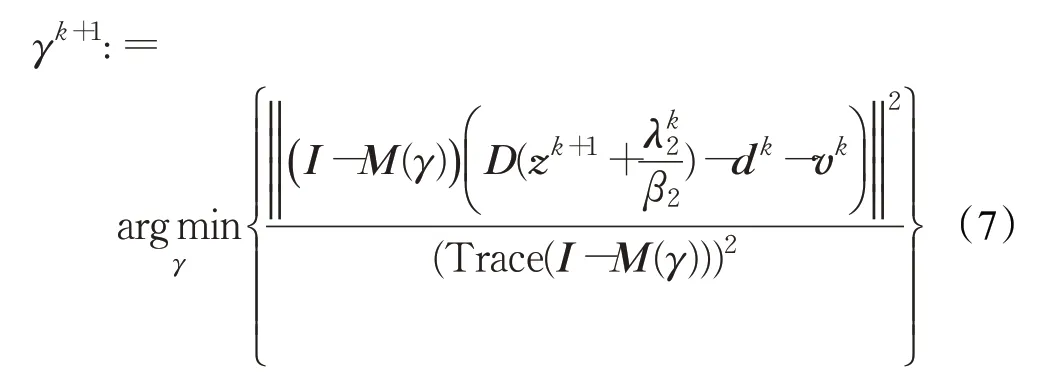
其中,I是单位矩阵,∇:=((∇(1))T,(∇(2))T)T,M(γ)=∇(∇T∇+γI)-1∇T。
由于∇(1)和∇(2)为周期边界条件下带圆块的块循环矩阵[20],故∇(1)和∇(2)可以通过傅里叶变换进行对角化,即∇(1)=F*Σ1F,∇(2)=F*Σ2F,这里Σ1、Σ2为对角矩阵,∗表示共轭转置。则:
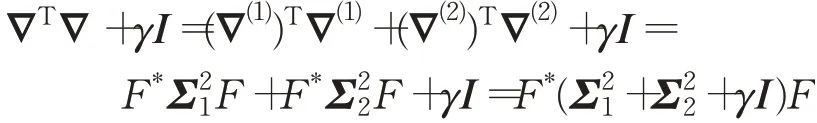
由于F*=F-1,则:
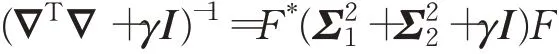
进一步,可得到:

其中:
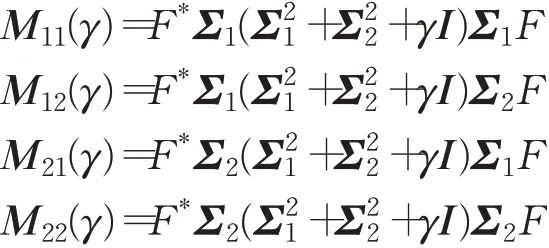
和
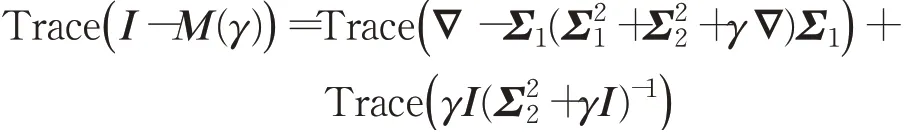
因此,通过一些基本的计算,求解优化问题(7)可以得到最优解γk+1。进一步,模型(3)中的参数可通过下面方式更新:

(2)求解关于uk+1的子问题
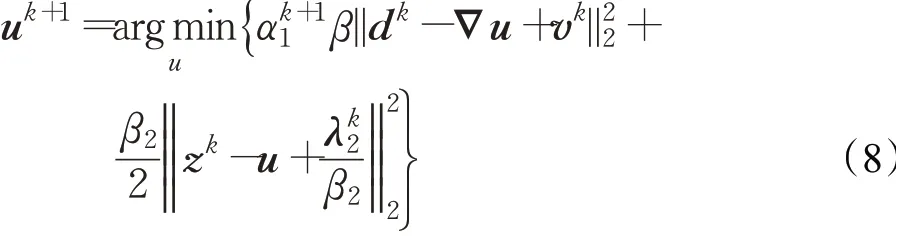
显然,u k+1满足:
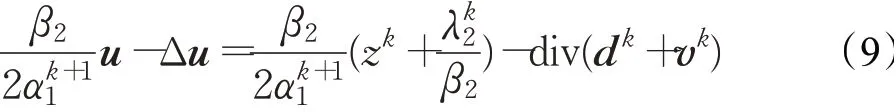
方程(9)为泊松方程,可采用Gauss-Seidel方法有效求解,其运算复杂度为O(N2),其中N为输入图像像素点的个数。
(3)求解关于v k+1的子问题

在周期性边界条件下,利用傅里叶变换可得到:

其中:

D是下列系数矩阵的行列式:
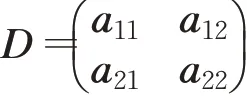
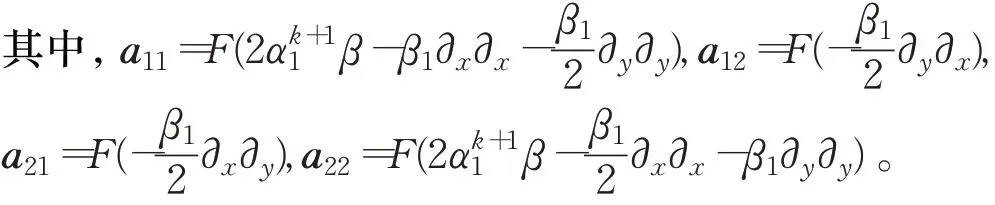
(4)求解关于d k+1,w k+1,z k+1的子问题

通过计算,可得到d k+1,w k+1有如下显示解:

另外,z k+1满足:

由于该子问题关于变量z严格凸,故最优解在导数为零处取得。通过求解λ(1-f/z)+λ2+β2(z-u)=0,可得:

综上,本文交替最小化算法的具体步骤为:
步骤1k=0,初始赋值
步骤2当迭代未停止时,重复以下子步骤:
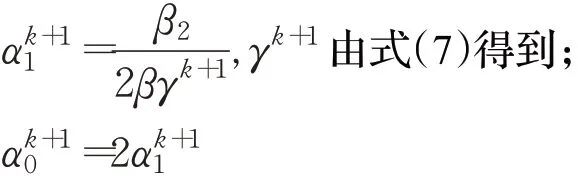
u k+1由式(8)得到;
v k+1由式(10)得到;
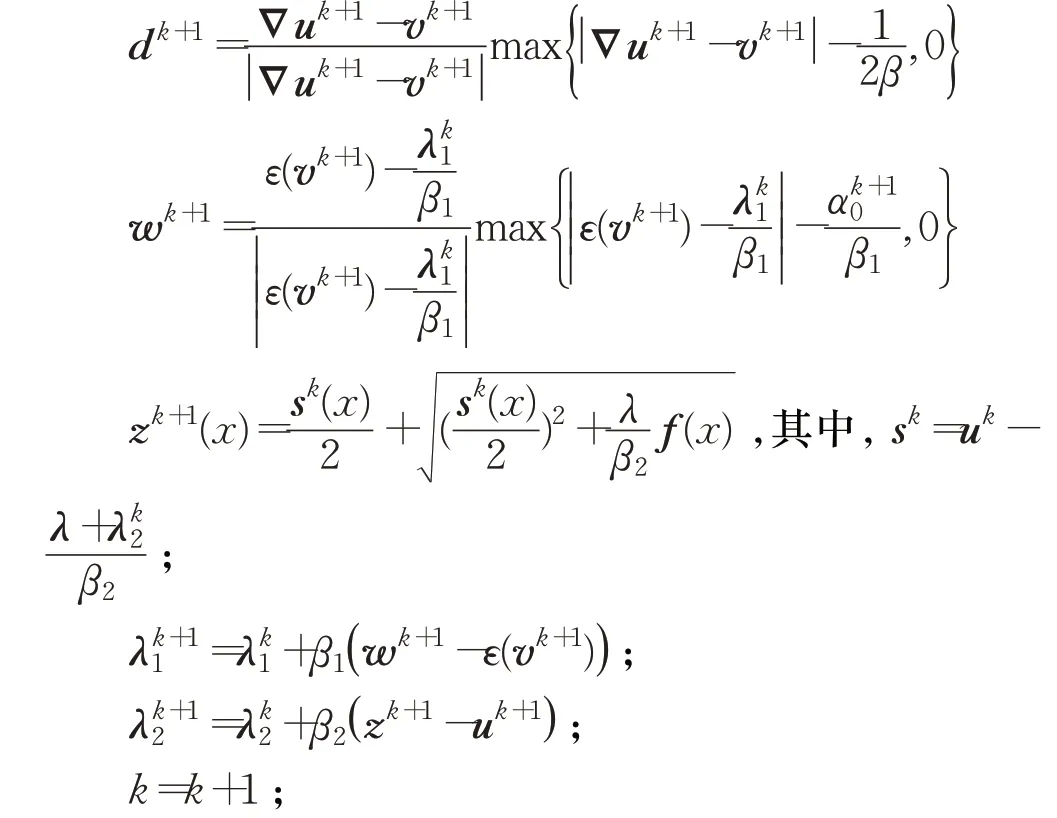
步骤3迭代终止条件停止迭代,求出u。
3 实验结果
本章将对多幅测试图像进行仿真实验,并同文献[12]中JY算法和文献[13]中ZJ算法进行比较,来检验本文算法的有效性。这里,用峰值信噪比(PSNR)和结构相似度(SSIM)[21]指标来定量分析不同模型的去噪效果,其定义形式如下:
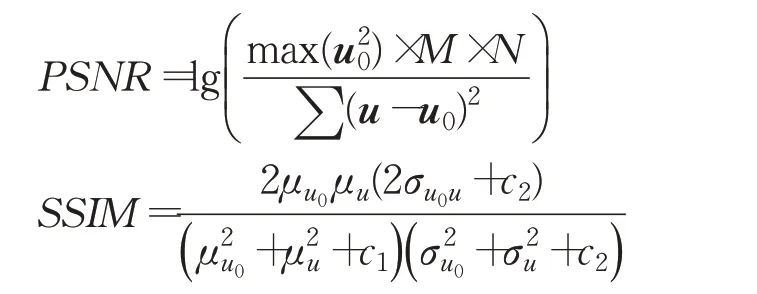
其中,u和u0分别表示恢复图像和原始图像,M×N是原始图像的大小,σu0和σu表示它们的标准差,σu0u是u0和u的协方差,c1和c2是常数。显然,较高的PSNR值和SSIM值意味着较好的去噪结果。为了保证不同算法之间比较的公平性,使用JY算法和ZJ算法的原始代码,并且通过调整各自算法中的参数,保证对文中的仿真实验,均取得最高的PSNR值。
本文选取5幅基准自然图像作为测试图像,如图1中第一列所示。这些图像分别被σ=0.07,0.11和0.15的泊松噪声所污染,作为文中观测到的泊松图像。

图1 三种算法的去噪效果Fig.1 Denoising results of three algorithms
3.1 参数的选取
对文中所有的测试图像和不同统计水平的泊松噪声,本文模型(3)中的参数设置如下:λ=0.1,α0=2α1,正则化参数α1通过本文算法自动更新得到,停止准则t ol=10-4。由于参数α1和α0可以在算法迭代过程中自动更新得到,因此这里讨论参数λ的取值对模型去噪结果的影响。以图1中的图片II的去噪结果为例,给出λ不同的取值与所得去噪结果的PSNR值的关系曲线图,如图2所示。观察曲线图2,不难发现:参数λ取值位于[0.05,0.5]之间时,对去噪结果的PSNR值影响较小,也就是说λ的取值对本文模型和算法的结果影响不大。因此,文中数值实验部分,都是固定λ=0.1,对于不同的测试图片,本文模型和所提算法均可得到较好的去噪效果。
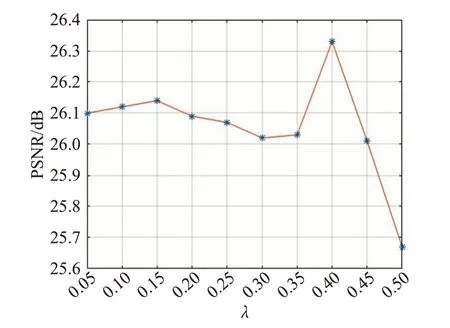
图2 λ与PSNR的关系曲线Fig.2 Relationship curve ofλand PSNR
在本文算法中,设置β初始值为45,随后每5次迭代β增加为1.5β,以这种方式保证参数β在算法迭代过程取值充分大直到算法收敛。在文献[22]中,作者已论证了该逼近方法求解的可行性。另外,对于增广Language函数中的惩罚参数β1和β2的取值,只要不是取得太大或者太小,对算法的去噪结果影响不大。因此,文中数值实验部分,固定取值β1=10,β2=15,对于所有的测试图片,均可取得较好的去噪结果。
3.2 本文算法的收敛性分析
下面仍以图片II的去噪结果为例,来分析本文交替求解算法的收敛性。给出实验中迭代次数与去噪结果PSNR值的关系曲线图,如图3所示。观察图3不难发现:本文所提交替求解算法在该实验中,当迭代次数超过30次以后,算法趋于收敛,所得去噪结果PSNR值趋于稳定。这个实验从某种意义下可以说明本文所提算法的收敛性。实际上,本文算法对于文中所有的图片,当迭代步数接近50次左右,算法均趋于收敛。
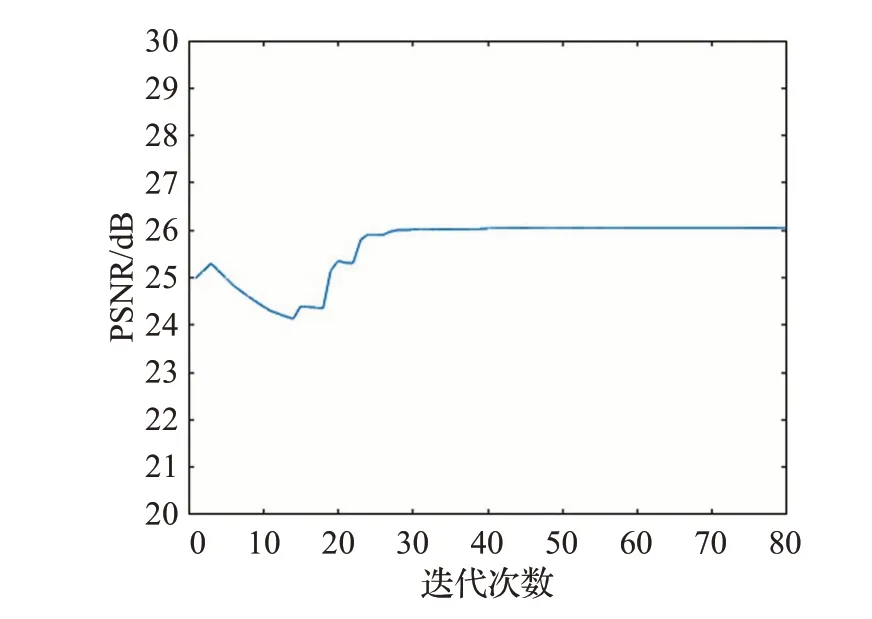
图3 迭代次数与PSNR的关系曲线Fig.3 Relationship curve of iteration numbers and PSNR
3.3 去噪结果
对图1中的5幅测试图片,分别加入3种不同统计水平的泊松噪声,JY算法、ZJ算法和本文算法针对这些噪声图像进行去噪,得到相应的PSNR值和SSIM值如表1所示。不难从表1中看出:对于不同水平的泊松噪声,本文算法均可得到最高的PSNR值和SSIM值,这说明本文算法去除泊松噪声的效果要优于JY算法、ZJ算法。
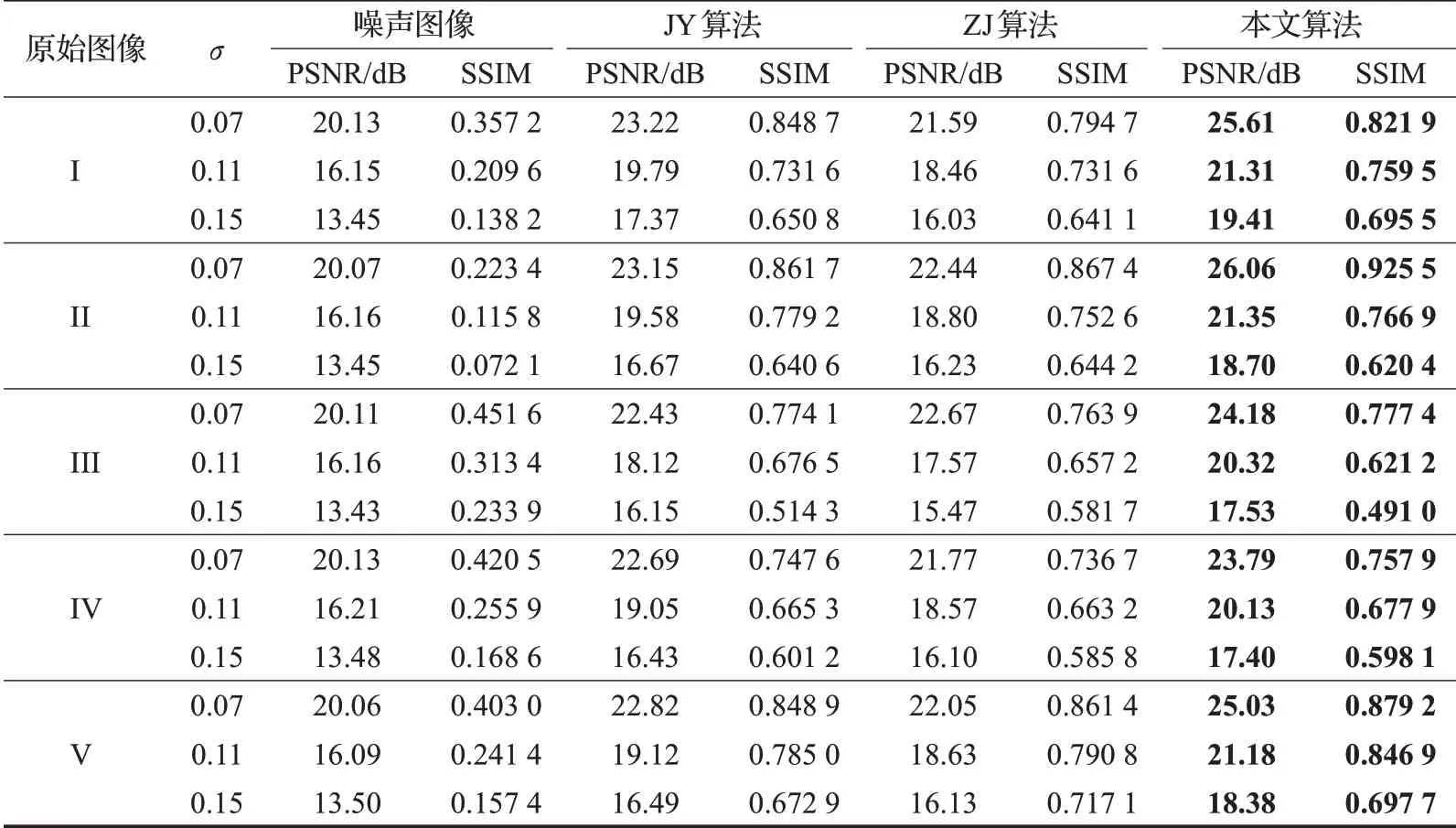
表1 不同算法的PSNR和SSIM比较结果Table 1 PSNR,SSIM values of different algorithms
为了更加直观地比较不同算法的去噪效果,本文测试了结构图像I和II,纹理图像III和IV,以及结构和纹理并存的图像V,图1针对带有σ=0.07的泊松噪声的测试图,展示了各种算法去噪后的图像。这里,第一列为原始图像,第二列为σ=0.07的泊松噪声图像,最后三列分别为JY算法、ZJ算法和本文算法的去噪结果,为了更清晰地展示本文算法在消除阶梯效应、保护图像边缘和纹理等细节方面的优势,在图4中给出了图1中部分结果区域的放大图像,这些区域在图1中已用红色方框标出。
由图1可知,对于图像I和图II中的平滑区域,JY算法和ZJ算法都产生明显的阶梯效应,而本文算法有效克服了上述缺点。从图像II的放大区域也可以观察到,本文算法有效去除了泊松噪声,且消除了光滑区域的阶梯效应等现象,具有更佳的视觉效果。
本文算法在处理纹理图像III和IV时,有效去除噪声的同时也能保留更多的纹理、结构等细节信息。从图4中图像IV的放大区域可以看出,本文算法所得结果在“头发”处保留了更多细节和对比度。
图V为结构和纹理并存图像,本文算法在处理此类图像时,有效去除噪声的同时也能保留更多的纹理,结构等细节信息并能消除光滑区域的阶梯效应等现象。从图4中图像V的放大区域可以看出,本文算法所得结果在“鼻子”周围保留了更多细节且能消除脸部平滑区域的阶梯效应。总的来说,从图1和图4中的去噪结果来看,本文算法不仅能有效地去除图像中的泊松噪声,还能产生较好的视觉效果。

图4 三种算法去噪结果的部分放大Fig.4 Zoom areas of denoising results with three algorithms
4 结束语
针对图像中的泊松噪声,本文从Lv模型出发,给出了一种自动选择正则化参数的交替极小化算法。数值实验结果表明,本文算法有效去除图像中地泊松噪声,同时还能抑制阶梯效应、保护边缘和纹理等细节信息。
