空间关键字查询综述

孟祥福，王丹丹，张 峰

辽宁工程技术大学 电子与信息工程学院，辽宁 葫芦岛 125105

空间关键字查询在实际中的应用越来越广泛，研究方面也逐渐增多。传统的空间关键字查询主要是同时考虑查询对象、查询点的位置信息和它们关键字的匹配程度的新型的查询处理类型，空间关键词查询具有重要的理论研究价值。空间关键字查询包含索引机制、查询模型和与其他技术结合的查询算法等三个方面。随着对空间关键字查询的研究，研究者们提出了多种索引结构，例如文本搜索的索引技术倒排文件（Inverted file）、签名文件（Signature file）和位图索引（Bitmap）等，基本的空间索引结构R-Tree，基于R-Tree改进的索引结构R+-Tree、R*-Tree，结合空间和文本索引技术的索引结构IR2-Tree、bR*-Tree、IR-Tree、Light-Weighted、两阶段索引等，基于IR-Tree的改进CIR-Tree、CDIR-Tree、WIR-Tree以及SIR-Tree等，其他索引结构VP-Tree、G-index索引、IRS-Tree、QuadTree、KR*-Tree、S2I等。

还有研究者对空间关键字查询处理模式改进，现有的对于空间关键字的查询处理模式主要可以分为4类：（1）布尔范围查询，该查询模式返回那些地理位置在查询区域内且文本描述包含所有查询关键字的兴趣点；（2）布尔kNN查询，该类方法用于检索文本描述包含所有查询关键字且距离查询位置最近的前k个空间对象；（3）top-k范围查询，用于检索位于查询区域内且与查询关键字具有最高文本相似度的前k个空间对象；（4）top-kkNN查询：该类方法根据空间对象的文本相关性和位置相近性进行top-k检索和排序，排序分数根据空间对象的文本描述与查询关键字的文本相似度和对象到查询位置的距离的权重进行评估。近年，又提出一种新的查询处理-反最近邻（RNN），反最近邻是由最近邻查询扩展而来的。

最后，传统的空间关键字查询通常是假定用户明确自己的查询意图并且仅支持严格查询匹配，但是随着用户需求的不断剧增，显然，这种简单的形式上的匹配已经不能够满足用户的需要。通常情况下，用户的查询意图是模糊或不精确的，用户往往会使用自己熟知的关键字表达查询意图，因此提出的关键字查询也并非能够有效表达出用户的查询需求，所以考虑语义近似、用户偏好等能够更好地满足用户的个性化查询需求。所以进而学者们提出了一些新的改进，结合语义近似或用户偏好进行查询。之前传统的空间关键字查询大多数在欧式空间上进行，但实际上，欧式空间的位置、距离并不与实际路线完全吻合，所以进一步研究了路网上的空间关键字查询。并且随着社会的发展和用户的实际需要，研究者们研究了路线规划查询、社交网络上的查询、基于影响约束下的查询等。近年，随着大数据与可视化的流行，研究者们也将目光放到了可视化技术上面，结合空间关键字和可视化进行查询。

1 索引结构

传统索引方法有哈希表和B-Tree。哈希表可以对数值进行精确匹配，但是不能进行范围查询。B-Tree是对键值的一维排序，但不能搜索多维空间。B-Tree是一种相对来说比较复杂的数据结构，尤其是在它的删除与插入操作过程中，因为它涉及到了叶子结点的分解与合并。除了传统的索引方法，还提出一些空间索引结构，就是指依据空间实体的位置和形状或空间实体之间的某种空间关系，按一定顺序排列的一种数据结构，其中包含空间实体的概要信息如对象的标识、外接矩形及指向空间实体数据的指针等。简单的说，就是将空间对象按某种空间关系进行划分，以后对空间对象的存取都基于划分块进行。

1.1 空间索引结构

R-Tree[1]：R-Tree是最基本的空间索引结构，Guttman在1984年最早提出。R-Tree是一种高度平衡树，由非叶子结点和叶结点组成，空间对象的最小边界矩形（Minimum Bounding Rectangle，MBR）存储在叶结点中，非叶子结点通过聚合其孩子结点的外接矩形而形成，根结点包含了所有这些外接矩形。R-Tree叶子结点存储结构形式(Rectangle,Obj),Rectangle表示围住叶子结点中所有空间对象区域的最小边界矩形MBR,Obj表示一个空间数据对象；非叶子结点存储结构形式(Rectangle,Child),Rectangle表示的是包围其所有子结点所在区域的MBR,Child是指向该非叶子结点的子结点。图1是RTree结点存储结构，如果该结点是叶子结点，E表示空间数据对象；若该结点是非叶子结点，E表示指向子结点的条目。

图1 R-Tree结点存储结构Fig.1 R-Tree node storage structure

R-Tree是B-Tree在k维空间上的自然扩展，R-Tree的优点是一种动态索引结构，即它的查询可与插入或删除同时进行，并且不需要定期地对树结构进行重新组织。R-Tree索引结构的作用在于，进行一个空间查询时，只需遍历少数几个中间结点即可定位到要找的空间对象（即逐渐缩小到某个区域进行查询），但是缺点是只能存储空间对象的位置信息，不能存储其文本信息。基于R-Tree改进的索引结构IR-Tree[2-3]、CIR-Tree[4]、CDIRTree以及SIR-Tree等也是当前的研究热点。R-Tree空间索引算法的研究应该做到：支持高维数据空间；有效划分数据空间，以适应索引的组织；实现多种查询方式系统中的统一。对于R-Tree的索引结构最新研究不应该仅仅为了加快某种查询方式或提高某个方面的性能而忽略其他方面的影响，这样可能会导致更多不必要的性能消耗。

R+-Tree：R+-Tree与R-Tree类似，主要区别在于R+-Tree中兄弟结点对应的空间区域无重叠，这样划分空间消除了R-Tree因允许结点间的重叠而产生的“死区域”（一个结点内不含本结点数据的空白区域），该索引结构的优点是减少了无效的查询，大大提高空间索引的效率，但对于插入、删除空间对象，由于操作要保证空间区域无重叠而效率降低。同时R+-Tree对存储跨区域的空间物体的数据是冗余的，随着数据库中数据的增加，冗余信息会不断增加。

R*-Tree[5]是R-Tree的变体，是在R-Tree的基础上对部分算法进行了优化改进，相对R-Tree优化的地方是强制重新插入算法。R-Tree的插入操作导致结点溢出时，采用分裂的方法进行处理，而R*-Tree对新的空间对象索引项的插入导致结点溢出时，它将会选择部分结点在同层结点间进行调整，以推迟结点分裂，从而达到优化R-Tree整体结构的目的。基于R*-Tree的空间索引算法优点是提高了空间的利用率，插入成本低于R-Tree，但缺点是增加了CPU代价。

下述例子描述R*-tree结构，R7～R14表示数据对象。采用空间分割方法构造R*-Tree，用最小边界矩形围住空间中的每个数据对象，然后将空间中彼此距离接近，使得矩形增加的面积最小的空间对象用更大的最小边界矩形包围起来。如图2中，由更大的最小边界矩形R4将彼此最为邻近的R8、R9、R10包围起来，用此方法将空间区域划分好后，将这些矩形存储到R*-Tree，图2中的数据对象所构成的R*-Tree结构如图3所示。

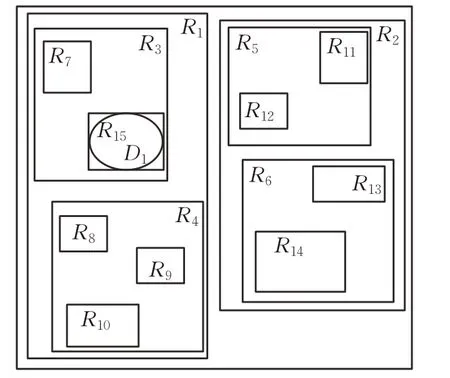
图2 数据对象Fig.2 Data objects

图3 数据对象所对应的R*-TreeFig.3 R*-Tree corresponding to data object

R-Tree及基于R-Tree改进的索引结构都只存储空间信息，较适合范围查询，R+-Tree不易实现不规则空间对象的任意查询。

1.2 空间文本混合索引结构

IR2-Tree[6]：MBR和签名文件Signature组成了IR2-Tree。它的优点是存储代价小、搜索效率高，但查询关键字必须严格匹配。图4显示使用表1的空间对象数据集的IR2-Tree示例。与R-Tree相比，IR2-Tree的结点中存储包含文本信息的签名文件，并且在这里签名文件被简化，每个比特为一个关键词：Shop，spa，internet，pool，launch，pet，1表示结点包含了对应的关键词，0表示不包含。

图4 表1对应的IR2-TreeFig.4 Corresponding IR2-Tree in Table1

表1 空间对象的样本数据集Table 1 Sample dataset of spatial objects

bR*-Tree[7]：R*-Tree+BitMap，R*-Tree结点包含MBR，并且有结点中所有关键字的位图和关键字MBR，它的优点是存储空间小，缺点是关键字匹配需求高，关键字多，I/O代价高。

IR-Tree：IR-Tree本质上是一个R-Tree，是由R-Tree和Inverted file构成，IR-Tree的每个结点含有倒排文件（倒排文件是用于复杂的查询，是一种特殊的文件结构）。对于IR-Tree的一个叶结点N，它的形式为(O,rectangle,O.di)，其中O是一个空间对象，rectangle是对象O的边界矩形，O.di是空间对象O的关键词信息。叶子结点还包含一个指向被索引对象的文本文档的倒排文件的指针。对于IR-Tree的一个非叶子结点R，它的形式是(cp,rectangle,cp.di)，其中cp是R的一个子结点的地址，rect angle是最小边界矩形（是查找、删除、插入操作的关键），cp.di是子结点伪文档的标识符。倒排文件中包含两个主要部分：（1）所有文档关键词；（2）一个记录列表集合，每一个记录里，对于一个关键词t有d表示包含t的文档，Wd,t表示t在文档d中的权重。它提高了搜索效率，所占的存储空间较小，允许查询关键字部分匹配。

图5描述8个空间对象O1,O2,…,O8的位置，表2描述了空间对象的文本信息，图6是图5的IR-Tree示例。

图6 IR-Tree索引Fig.6 IR-Tree index

表2 空间对象的文本信息Table 2 Text information for spatial objec

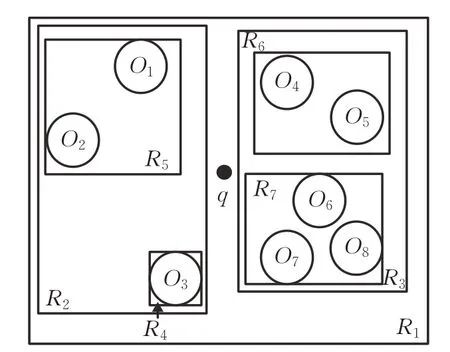
图5 空间对象及边界矩形Fig.5 Spatial objects and boundary rectangles

Light-Weighted[8]将R*-Tree和Inverted file分开存储，R*-Tree结点包含MBR和结点到根结点路径的Label，倒排结点包含标记位置组成它的可扩展性较强，搜索效率高，但存储代价高，需要频繁进行插入操作，导致计算代价过高。

两阶段索引[9]，它是由R-Tree和Inverted file构成的，其中R-Tree结点包含MBR，倒排文件结点包含关键字信息。具有结构简单的优点，但存储代价高，无法确定第一阶段产生的候选对象个数。

空间文本混合索引结构是空间和文本索引技术的集成，能够同时存储位置和文本信息，IR2-Tree和bR*-Tree对关键字匹配要求较高，适合对关键字进行精确匹配的查询；IR-Tree允许查询关键字部分匹配，比较适合top-kKNN查询。

1.3 其他索引结构

VP-Tree[10]：1993年被提出，VP-Tree是二叉空间划分树，随机选取某数据点作为制高点，计算其他点到制高点的距离并根据制高点的距离划分点。求出距离中值，小于中值的数据分给左子树，大于中值的数据点分给右子树，递归建立左子树、右子树，VP-Tree作用于任何度量空间，可利用VP-Tree做k近邻查询，图7是VPTree的一个例子，选取<5，6>为制高点。

图7 VP-Tree例子Fig.7 Example of VP-Tree

QuadTree[11]：其区域搜索效率较高，但是树结构不平衡，动态性差，存储代价较高。QuadTree是将已知范围的空间划成四个相等的子空间，并且子空间可以继续划分直到一定深度或满足某种要求，图8是VP-Tree的一个例子。一些QuadTree的改进是将QuadTree和结点中文本信息对应的倒排文件组成，例如IL-QuadTree[12]。

图8 四叉树示例Fig.8 Example of quadtree

G-index索引[13]：聚类标准+聚类操作，通过聚类操作。但是，可泛化成其他索引结构。具有通用性，但是有较高的泛化计算代价，存储代价较高。

IRS-Tree[14]是一种拥有Synopses的倒排R-Tree的混合索引结构，能够有效处理一组位置敏感等级查询。基于IRS-Tree的查询算法要求提供数值属性的精确范围，这样可能会导致过少甚至没有查询结果返回。

此外，还有一些其他的索引结构，例如Hariharan等人提出KR*-Tree（关键字R*-Tree）。KR*-Tree的每个结点实际上都被一组关键字扩充了，这些关键字出现在以该结点为根的子树中。KR*-Tree的结点被组织成倒排的列表，对象也是如此。在文献[15]中提出了一种新的索引来提高top-k空间关键字查询的性能，即空间倒索引（Spatial Reverse Index，S2I）。Wu等人[16]提出了WIR-Tree，其目的是将对象划分为多个组，使不同的组尽可能少地共享公共关键字。

QuadTree适合空间对象分布均匀的查询。VP-Tree通过选择空间中的制高点，并将数据点分为两个分区来分离度量空间中的数据。因此，可以使用VP-Tree来查找在特定点附近沿距离方向的数据，适合范围查询和近邻查询。IRS-Tree适用于包含数值属性的空间对象，但需提供数值属性的精确范围。

1.4 文本索引

文本搜索的索引技术有：倒排文件（Inverted file）、签名文件（Signature file）和位图索引（Bitmap）等。它们主要集中于关键字的精确匹配，但由于文本表达形式的多样性，可能导致结果太少。

现有的索引技术主要分为空间索引、文本索引和空间文本混合索引，各个索引有不同的优点，但是同时它们也存在不足之处，文本索引需要精确匹配，所以得到的结果有时候不能满足用户的需求。空间索引包含RTree和基于R-Tree改进的索引结构、VP-Tree、QuadTree及对其的改进索引结构、G-index等。R-Tree是比较基础的且被利用得较多的一种索引结构，但是R-Tree不能存储文本信息；R*-Tree对R-Tree整体结构优化，但是CPU代价较高；QuadTree搜索效率较高但存储代价大；G-index具有通用性，但泛化计算代价高。现有的空间文本索引大多是将空间索引技术和文本索引技术结合，例如，BR*-Tree将R*-Tree和Bitmap结合；IR-Tree将RTree和Inverted file结合；IRS-Tree还考虑了包含空间对象的数值属性信息，但是需要提供数值的精确范围，具有一定的局限性。

2 空间关键字查询处理模式

现有的对于空间关键字的查询处理模式主要可以分为4类：布尔范围查询、布尔k近邻（KNN）[17]查询、top-k范围查询[18]和top-k k近邻查询[19]。布尔范围查询返回文本描述包含所有查询关键字且地理位置在查询区域内的兴趣点。需要精确匹配文本，而且不能控制查询结果规模、不能对查询结果进行排序。布尔k近邻（KNN）查询用于检索文本描述包含所有查询关键字且距离查询位置最近的前k个空间对象，它是通过查询点与兴趣点之间的距离对查询结果进行排序，排序先后与距离大小成反比。上述两种查询方法都需要所有文本精确匹配，这将会导致没有结果或很少的结果被返回，或者是查询结果与查询点位置较远。top-k范围查询用于检索位于查询区域内且与查询关键字具有最高文本相似度的前k个空间对象，其结果只能包含部分关键字，但是该方法并没有考虑位置相关性。top-k k近邻查询根据空间对象的文本相关性和位置相近性进行top-k检索和排序，根据空间对象的文本描述与查询关键字的文本相似度以及对象到查询位置的距离的权重来评估排序分数。

近年，提出一种新的查询处理-反最近邻（RNN），反最近邻查询是在最近邻查询的基础上提出来的，反最近邻问题本质上就是数据集中某些点所带来的影响集的问题，比如一家咖啡馆要在某个商场开店，这就必定会对周边的一些咖啡店或者饮品店带来客户上的影响，其中受影响最大的咖啡店或饮品店就是想要的结果，也是RNN查询最终的目的，RNN应用广泛成为一项重要的研究。对RNN查询的研究主要是基于R-Tree及其扩展进行的，这样引入了R-Tree的缺点。Korn等人[20]提出一种RNN查询算法，基于R*Tree构造了RNN-Tree（Reverse Nearest Neighbor Tree，RNN-Tree）来实现查询，但是这种方法的缺点主要在于动态情况下需要建立两个索引，而且由于存储区域较大的重叠导致性能降低。Yang等人[21]提出一种基于RDNN-Tree（R-Tree containing Distance of Nearest Neighbor）的RNN查询算法，该算法有效地避免建立两个索引结构，提高了查询效率。然而，RDNN查询仅仅对低维数据有效，并且随着维数的增加，RDNN查询性能会因为R*-Tree的限制而急剧下降。郝忠孝等人[22]提出了基于SRdnn-Tree（SR-Tree containing distance of nearest neighbor）索引结构的RNN查询算法，突破了R*Tree在高维数据空间查询的局限性。李松等人[23]使用Voronoi图和空间划分区域的性质计算查询点的反最近邻，并结合R*Tree构造了一种新的基于Voronoi图的索引结构（Voronoi diagram-based Reverse Nearest Neighbor query Tree，VRNN-Tree），基于该索引结构的RNN查询适用于平面和复杂曲面上的数据点。王淼等人[24]提出了一种新的基于Delaunay图的索引结构Delaunay-Tree用来解决反最近邻问题，将查询点作为Delaunay图的一个生成点，利用Delaunay图的生成点与其邻接生成点之间的关系来查询数据集中的反最近邻。

2013年，Jiang等人提出了top-k组反最近邻查询，识别并解决了一种新的查询，即反向top-k组最近邻（RkGNN）查询。他们定义了RkGNN查询（GNN的一种变体），以最佳优先方式搜索[25]，并使用当前条目e与查询对象q之间的最小距离作为排序键。然后，他们采用了一些有效的修剪启发式算法来剔除不合格的候选子集，利用排序和阈值机制来缩小搜索空间，并充分利用了惰性修剪和空间修剪技术的优点有效地处理了RkGNN查询，即开发了两种算法LRkGNN（惰性LRkGNN）和SLRkGNN（空间修剪LRkGNN）来有效地解决top-k组反最近邻查询。之后，Cheema等人[26]研究了反k最近邻（ReversekNearest Neighbor query，RkNN）和反top-k查询，并利用基于区域修剪的算法和线性评分函数对SPTk（Spatial reverse top-k）查询进行了优化。Wang等人[27]研究了基于动态轨迹的反k最近邻查询，提出了RkNNT（ReversekNearest Neighbor search over Trajectories）算法来解决动态路线规划问题。Wang等人[28]改进了传统的基于位置查询的反k最近邻查询算法，利用递增的临时网络扩展树更新道路网络的权重变化，从而实现动态监测目标的结果。Hidayat等人[29]在影响区域的基础上提出了影响因子的概念，同时利用新定义的修剪圆对空间进行修剪，筛选合适的数据，从而提高RkNN查询的效率和准确性。Guillaume等人[30]提出了一种近似求解RkNN查询的方法，该方法基于内在维度的特征优化修剪操作，降低了预处理成本，并提高了在高维度时的查询性能。Francisco等人[31]分布式的思想应用于处理RkNN查询，利用无共享空间云基础架构Spatial Hadoop和Location-Spark设计分布式RkNN查询算法，提高了分布式空间数据管理系统的效率和可扩展性。

最近，刘润涛等人[32]提出了一种基于新型索引结构的反最近邻查询，先定义空间物体间的4种序关系，然后利用这些序关系提出了一种新的索引结构：MBDNNTree（index Tree based on the Minimum Bounding square and the Distance of Nearest Neighbor），这种索引结构运用了R-Tree中分割数据空间的思想，将数据点集通过最近邻距离扩展为空间物体，继而利用其中多种序关系优化索引结构，将空间位置相近的数据尽可能地存储在同一结点中，使得该索引结构中同层结点之间均满足同一种序关系，运用该关系，给出进行RNN查询的高效修剪规则，再对中间结点进行较少量的简单计算即可有效地减少了结点的访问数量，从而提高查询效率。

3 其他技术结合的查询算法

3.1 空间-文本查询

传统的空间关键字查询将用户位置和用户提供的关键字作为参数，并返回与这些参数在空间和文本上相关的web对象。文献[2-3，6，15，33-40]在研究空间-文本查询的不同方面做出了一系列的贡献。在文献[2-3，15]中，研究了欧氏空间中top-kkNN查询。一些工作[2，6]主要集中在需要精确关键字匹配的空间关键字布尔查询（SKBQ），但是很明显，由于文本表达的多样性，它们可能导致返回结果太少或没有。为了克服这个问题，研究人员最近[15，35，38]提出了一些新的索引结构去支持空间关键字近似查询（SKAQ），这些结构能够处理在实际应用中经常出现的拼写错误和传统拼写差异（例如“theater”和“theatre”）。

空间对象的位置信息通常由经纬度表示，因此对于空间对象位置的度量是至关重要的，现有的方法大多可以计算位置间的距离，几种比较常用的方法例如欧氏距离、马氏距离、曼哈顿距离、切比雪夫距离和余弦相似度。现有的文本相似度的计算方法：内积法、余弦法、Dice系数法、Jaccard系数法、基于向量空间模型等。

但传统的空间关键字查询主要关注空间和文本相似性，忽略了用户偏好、语义近似等方面。

3.2 语义近似查询

现有的空间关键字查询方法主要关注空间和文本相似性，忽略了对空间Web对象和查询中关键字的语义理解。由于对对象和查询中的语义缺乏理解，它们仍然无法检索与查询中的关键字同义但完全不同的对象，如“theater”和“cinema”。这种差异促使研究其他语义感知的方法，以捕获空间关键字的语义含义。在文献[37，41]中研究了具有语义的空间关键字查询，其目标是找到在空间邻近性和语义相关性方面最优的对象。Qian等人[42]定义了一种新的空间关键字查询，它同时考虑了空间、文本和语义相似性。提出新颖的索引结构，即NIQTree和LHQ-Tree，该结构以一种分层的方式将空间、文本和语义信息集成在一起，以便在查询处理时有效地修剪搜索空间。采用了一种改进的基于iDistance[41]的混合索引结构NIQ-Tree[43]。通过利用iDistance绘制主题分布，NIQ-Tree将支持同时对空间、文本和语义维度进行有效的修剪。可以避免在高维空间中索引所有对象时出现大量的死空间。但由于“维数灾难”，算法[44]性能受到大量潜在主题的影响。所以他们进一步设计了一个基于局部敏感哈希（LSH）的混合索引结构，称为LHQ-Tree，它能根据查询的空间、文本和语义一致性，避免扫描无希望的对象。在LHQ-Tree的基础上，提出了一种新的查询处理机制，基于一定的理论边界有效地裁剪搜索空间。

现有的语义相似度计算方法：（1）通过本体定义术语/概念之间的距离定义拓扑相似性来估计语义相似性。（2）通过向量空间模型等统计手段估计语言单元（单词、句子等）之间的语义相关性。（3）利用概率主题模型对文本信息进行语义相似处理。通过主题模型可以测量文本与主题之间的语义关系，也可以测量不同文本之间的语义关系。现已有很多经典的主题模型：Latent Dirichlet Allocation（LDA）[43]、Dynamic Topic Model[45]、Dynamic HDP[46]、Sequential Topic Models[47]等。

3.3 基于路网的查询

已有的研究大多数集中在欧式空间中如何有效处理空间关键字查询，但事实上人们的日常生活是被路网约束的，空间邻近性应该由最短路径距离而不是欧氏距离来决定，在欧式空间查询的最优结果在实际中不一定是最优的结果。所以现在一些工作研究了一个新的问题，即在路网上进行空间关键字查询。与欧式空间相比，基于路网的空间关键字查询的研究更具有现实的意义和价值，也给研究者们带来了更大的挑战。

Rocha-Junior等人[48]首次解决了在路网上处理top-k空间关键字查询的问题，该文利用覆盖网络使查询处理更高效。例如，图9展示了一个景点的路网和空间文本对象。圆圈表示空间文本对象o,q.l表示查询位置。假设一名游客在q.l带着一部手机并提出一个top-k空间关键字查询，寻找“hotel”。如果是欧式空间中的传统查询，O9将作为top-1结果，但是考虑路网后，top-1结果是O6。在路网的top-k空间关键词查询中，同时考虑了最短路径和文本相关。

图9 从波士顿大学到波士顿市中心的路线Fig.9 Route from Boston University to downtown Boston

文献[49]首次提出了路网中连续的top-k空间关键字查询，提出了两种以增量方式遍历网络的方法，即以查询为中心的算法（QCA）——从查询位置所在的边的结束结点开始遍历网络，直到找到top-k结果为止。同时，它维护了一个扩展树，以避免后续处理时不必要地遍历一些网络边缘。和以对象为中心的算法（OCA）——从与查询关键字相关的对象开始遍历。这样，经过初始处理后，构造出一棵最短路径树，后续处理可以利用这棵树显著减少遍历的边数。原则上，这两种方法都可以通过查找感兴趣的对象来减少问题，从而将查询转移到检查静态网络结点，减少连续监控时不必要的重复遍历网络边缘。

上文提及的文献[28]利用递增的临时网络扩展树更新道路网络的权重变化，从而实现动态监测目标的结果。文献[50-53]将top-kkNN查询应用于路网。Cho等人[50]提出了一种新的算法ALPS来对路段对象进行分组，并将分组对象转换为数据段，从而实现最小化数据对象的数量。此外，Rocha-Junior等人[52]提出了一种提高查询处理性能的新算法，该算法避免了在查询执行过程中检查数据对象的空间邻域。与此同时，文献[53]提出了一个新的问题：利用社会影响（RSkNN）对路网进行kNN搜索。但现有的路网空间索引不能够支持大规模的路网环境，而且目前基于路网环境下的查询方法能够处理考虑位置邻近和文本相似的空间关键字查询，但对于考虑用户偏好的空间关键字查询还不能够有效地处理。

3.4 路线规划查询

路线规划查询旨在找到满足用户需求的最优路线，比如可以利用基于关键字的最优路线查询为用户规划包含用户所有感兴趣的旅游景点并且花费较低的一条路线。例如Li等人[54]在空间数据库和路网中提出了一个旅行计划查询（Trip Planning Query，TPQ），其中每个空间对象都有一个位置和一个类别。查询的目的是找到起点和目标位置之间的最短路径，并且该路径需要通过用户指定的每个类别中的至少一个对象。例如，一个用户要从波士顿大学到波士顿市中心，他在途中想要经过ATM机、加油站和希腊餐馆，目标是为他提供可能的最佳路线（根据距离、交通、道路状况等），这个查询的困难在于每个类别都有多个选择，对于这个查询，存储上述类别（以及其他类别）对象位置的数据库，应该有效地计算出最小化总旅行距离的可行行程。另一种应该是提供一种能使总旅行时间最小化的行程。

图9（a）和（b）展示了文献[54]中的例子，从波士顿大学（1）到波士顿市中心（2）需要途经加油站（3）、自动取款机（4）和希腊餐馆（5）。在图9的例子中，用户明确地选择了一条包括ATM机、加油站和希腊餐馆的路线。显然，该系统不仅可以对停下的顺序重新排列以优化这条路线，也能为用户建议用户所不知道的其他选项（例如在地图上所示的大量的自动取款机）。

Sharifzadeh等人[55]研究了TPQ的一个变体，称之为最优顺序路由查询（OSR）。在OSR中，对查询类别施加总顺序，只指定起始位置。另一个例子是Cao等人[56]提出的关键字感知最优路由（Keywords-aware Optimal Route，KOR）搜索查询，该查询发现目标分值最小且路由的预算分值小于某一阈值的路由，同时覆盖所有查询关键字。并且前文提到的文献[27]提出了RkNNT算法，解决动态路线规划，该算法研究了基于动态轨迹的反k最近邻查询。

3.5 社交网络查询

有一些研究者们没有考虑上述部分，而是考虑身边朋友的影响，关注于社交网络中的查询。比如，Yang等人[57]提出了一个社会空间组查询，该查询选择一组附近的具有紧密社交关系的参与者。要求与会者到集合点的空间距离最小，同时满足一定的社会约束。

Lappas等人[58]研究了在社交网络中寻找专家团队的问题。目标是从社交网络找到一群人，每个人都有特定的技能，这样他们可以合作完成一项任务，使他们的沟通成本最小化，这项工作不考虑空间方面。文献[58]中一个社交网络查询例子，现在要建立一个工程师团队来完成一个项目，这些项目需要以下方面的技能：算法、软件工程、分布式系统、web编程。同时假设有5个候选对象{O1,O2,O3,O4,O5}，他们具有以下背景：XO1={软件工程，分布式系统，web编程}，XO2={web编程}，XO3={软件工程，分布式系统}，XO4={软件工程，分布式系统，web编程}，XO5={算法}。但一个项目的成功不仅取决于参与人员的专业知识，还取决于他们作为一个团队如何有效地协作、沟通和工作。所以下面用图10所示的社交网络表示了这些候选对象之间的关系，其中图中两个结点之间存在一条边，说明对应的人可以有效地协作。

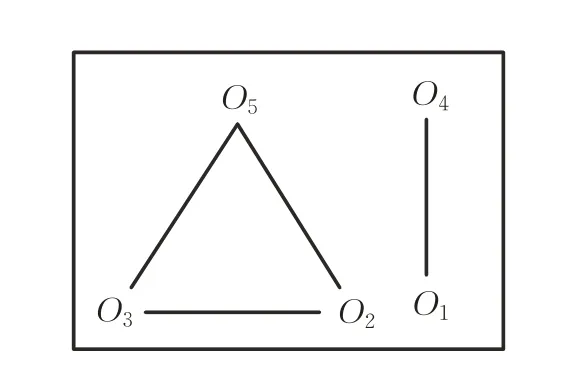
图10 {O1,O2,O3,O4,O5}中个体之间的社交网络Fig.10 {O1,O2,O3,O4,O5}social networks among individuals

在上述例子中，如果不考虑团队成员的协作效率，团队{O2,O3,O5}或{O1,O5}都可以满足所需的技能，但如果考虑团队成员的协作效率，根据图10可以得出团队{O2,O3,O5}是最优解，图中结构表明O1和O5不能一起工作，因为同一组或部门的人比在不同部门工作的人更容易沟通。

3.6 空间关键字组查询

现有的空间关键字查询方法主要侧重于寻找单个POI，但是单一对象可能不容易满足用户的需求，所以最近一些关于空间关键字查询的研究侧重于寻找一组对象作为满足用户需求的解决方案[57，59-69]，称为集合空间关键字查询（CSKQ）。CSKQ目的是给定用户的查询位置和关键字，将查找一组对象，这些对象覆盖查询的关键字，且接近查询的位置，同时组内对象也互相接近。例如，一个游客可能有特定的购物、餐饮和住宿需求，所以最好由几个空间web对象，来更好地满足该游客的需求，这些web对象必须涵盖所有查询关键字，彼此互相接近且都接近查询位置。近几年集合空间关键字查询（CSKQ）在空间文本数据库领域受到了广泛的关注。

Cao等人[60]提出高效处理空间关键字组查询，解决了三个实例化的检索top-k组的问题，设计了精确解和具有可证明的近似解，并研究了合并了对象权重的问题的加权版本。

Yu等人[61]提出新的个性化空间关键字查询问题——集合关键字偏好查询（Collective Keywords Preference Query，CKPQ）。首先设计了基于访问历史和潜在POIs主题的用户偏好模型，然后可以根据集合内的距离、查询位置的距离以及集合关键字的可达性（由POI流行度和拥塞度确定，避免在高峰时间访问受欢迎的POI）构造一个成本函数，根据该模型计算候选群体的成本。还提出了一种基于IR-Tree和修剪策略的高效算法，可以找到一个CKPQ的解来实现多个优化目标之间的平衡。

Park等人[62]定义了反向集合空间关键字查询（Reverse Collective Spatial Keyword Query，RCSKQ）。它是一种新颖的反向空间关键字查询，用于查找CSKQ中包含查询对象的所有用户。提出了两种新的过滤策略，一种是利用改进的G-Tree索引结构（具有最大距离的反向GTree）来解决计算开销问题的用户过滤策略。G-Tree是一种改善最短路径问题计算性能的路网指标结构。另一种是无索引结构的启发式过滤，减少搜索空间。

在文献[8，63]中，Zhang等人提出了一种新的空间关键字查询，称为m-最近邻关键字（mCK）查询，其目的是找到与m个用户指定关键字匹配的空间最近邻元组。Cao等人提出了集合空间关键字查询问题（Collective Spatial Keyword Query problem，CoSKQ），即检索所有对象中包含的关键字共同覆盖查询关键字的一组对象[59-60]。值得一提的是，以往的工作仅针对欧式空间中的CoSKQ问题，Gao[64]、Su[65]等人研究了路网上的空间关键词集合查询处理问题。

3.7 基于影响区域约束下的查询

基于影响区域约束下的查询，查找距离与用户查询关键字最相关的特征对象的最近的兴趣对象作为候选结果，这种查询方式有效地避免了遗漏查询结果以及与用户关键字不匹配的情况。早期，文献[70]研究了基于反向最近邻查询的影响集合，在该查询中，给定一个查询点，查询查找一组使得该查询点受到影响最大的集合。Hidayat等人[29]在影响区域的基础上提出了影响因子的概念，同时利用新定义的修剪圆对空间进行修剪，筛选合适的数据，从而提高RkNN查询的效率和准确性。

然而，由于影响区域约束需要检索全部空间区域，在大数据量情况下会导致较低的查询效率。在文献[70]中，查询返回的是一组使得查询点受到影响最大的集合，而Cai等人研究了基于特征对象的偏好查询，查询返回一组排序的兴趣点，这组兴趣点以及兴趣点周围特征对象均满足用户偏好。Cai等人考虑了查询对象周围其他对象属性满足用户偏好的程度，研究了欧式空间下基于影响约束的top-k空间关键字偏好查询，提出了两种有效的查询改进算法：（1）阈值倒排文件算法TFIFA，通过阈值剪枝策略为每个R*-tree结点计算一个上界分数，对上界分数小于或等于当前阈值的结点以及结点包含的子树进行剪枝。（2）基于贪心策略的最近邻查询算法GS-NNA。结合贪心策略和最近邻方法，每次选择文本相关度最高且满足阈值判定条件的特征对象，将距离该特征对象最近的空间对象加入到候选结果集中，一定能够从候选结果集中获得满足用户需求的查询结果。有效满足了用户的个性化top-k查询需求，并提高了查询效率。然而，上述基于影响区域约束下的查询，仅在欧式空间下考虑，而现实中两个兴趣点之间的距离大多都是基于路网环境，因此考虑路网环境下的查询具有更多的实际应用价值。

3.8 其他相关技术

李盼等人[71]构建一种新的混合索引结构AIR-Tree，能够同时支持文本和语义匹配，并利用Skyline方法对数值属性进行处理，最终利用评价函数对候选集进行个性化排序的混合索引结构。该文利用LDA主题模型来实现空间对象的语义近似查询的方法，并且利用Skyline对数值属性进行处理，实现了查询结果的个性化。提出的算法不仅支持空间关键字的精确匹配，并可以支持语义近似查询和形式上的近似匹配，且能处理文本信息中的数值属性，这样更符合用户查询要求，在一定程度上提高了用户体验以及满意度。

Luo等人[72]提出了一种新的分布式索引方案NPD index，在分布式设置中回答两类空间关键字查询。文献[73]使用关键字进行空间偏好查询的并行和分布式处理，提出并解决了一个新问题，即使用关键字对大规模分布的空间文本数据进行空间偏好查询的并行/分布式评估，进一步提高了算法的性能，从而降低了处理成本。

另外，文献[61，73]等均在空间关键字查询中考虑了用户偏好，更好地满足用户的个性化需求。

近几年，随着可视化技术的流行，也有一些工作[74-75]结合空间关键字查询与可视化技术进行查询。文献[74]提出一种基于自然语言的不确定人体轨迹可视化查询方法：（1）从文本语句中提取时空约束，并支持对不确定移动轨迹的有效查询方法。（2）利用POI及其所覆盖区域的语义信息对大量的空间不确定移动轨迹进行编码，将轨迹文档存储在文本数据库中，并采用有效的索引方案（根据提取的条件查询轨迹，首先，城市空间被小的可能空间区域（PSR）细分，以容纳不准确的采样点。其次，将轨迹转换为包含区域POI信息的文档，使用特殊的索引方案存储在数据库中。然后使用概率检索算法（Okapi BM25[76]）找到匹配输入条件的top-kPOIs，并利用潜在Dirichlet分配（LDA）主题建模发现的区域POIs的功能主题进一步增强。最后，使用top-kPOIs提取数据库中的相关轨迹。一旦获得了一组轨迹，将根据计算出的每个轨迹的相关得分对它们进行排序。并且提供了一个有序的结果列表）。可视化部分：查询条件规范视图构建可视化分析系统，用于指定查询和可视化地调整查询条件；在地理环境下可视化轨迹的地图视图；做了一组可视化，包括时间图视图、语义视图和用于检查查询结果的详细结果视图。

4 结束语

空间关键字查询在实际中的应用越来越广泛，研究方面也逐渐增多，到目前为止学者们已经做了很多的努力来支持有效的空间关键字索引和查询。传统的空间关键字查询通常是假定用户明确自己的查询意图并且仅支持严格查询匹配，但是随着社会的发展和用户的实际需要，显然这种简单的形式上的匹配已经不能够满足用户的需要，所以对空间关键字查询有了进一步的研究。本文从索引机制、查询模型和与其他技术结合的查询算法三个方面对空间关键字查询的研究进展进行综述。但是目前的研究还存在着值得进一步研究的问题：

（1）时间约束

考虑空间和文本信息的同时，加入时间约束对空间关键字查询具有一定的意义，根据用户对时间的需求可以返回更能满足用户需求的结果，但同时这会增加问题的复杂度和技术实现的难度。所以在未来工作中，在这个问题中，应该更多地考虑如何解决时间约束带来的复杂度和技术问题。

（2）查询结果的多样性

现有的集合空间关键字查询的一些研究工作中，虽然能够查找到覆盖所有查询关键字的一组对象，但是这一组对象可能会重复出现某个关键字，忽略了组内对象的多样性。因此未来工作中，在选取空间对象进行组合时，应该避免选取具有相同关键字的空间对象作为一组；或在最终选取查询结果时，考虑空间对象之间的多样性对排序结果的影响。

（3）查询结果的可视化

通过结合可视化，能够更直观地表达和分析查询条件、结果，所以在未来的研究工作中可以考虑更多更丰富的可视化方法，可以将空间关键字查询与地图、图表等结合起来。可以结合地图的地理条件、自带的一些功能等做查询，并且还可以通过在地图上展示查询结果，甚至可以对查询结果在地图上做路线规划等。