自调优自适应遗传算法的WKNN特征选择方法

陈倩茹，李雅丽，许科全，刘铱龙，王淑琴

天津师范大学 计算机与信息工程学院，天津 300387

随着大数据时代的到来，高维数据集的处理已不可避免。训练时间随着特征空间维数的增加而增加，不断增加的维度会导致“维度诅咒”的问题[1]。特征选择是解决“维度诅咒”问题的重要降维方法之一[2]。通常情况下，分类器处理的数据集中存在许多冗余或不相关的特征，这不仅增加了训练时间，而且降低了学习后分类器的分类精度。特征选择是克服这类问题的一项重要的数据预处理技术，它涉及到从原始的特征空间中选择相关特征的最小子集，从而减少训练时间，提高学习性能[3]。

在过去的几十年里，特征选择算法得到了广泛的应用。根据特征选择搜索如何与分类模型的构建相结合，特征选择方法一般分为三类：Filter、Wrapper和Embedded[4]。Filter方法通过只考虑数据的内在属性来评估特征的相关性，并基于统计或信息度量选择高级特征。Wrapper方法利用所选特征训练分类器，根据分类器在测试集上的表现来评价所选特征。Embedded方法在考虑分类器构造的同时，筛选出关键特征。

K近邻（K-Nearest Neighbors，KNN）算法是一种基于对象相似度的原型方法，常用于解决分类和回归任务[5]。近年来，K近邻被扩展成不同的方式，应用于特征选择。Park等[6]提出了一种基于最近邻集成分类器的Wrapper特征选择方法。该方法利用序列随机K近邻（SRKNN）作为随机森林在高维数据建模中的替代方法，通过迭代过程寻找重要特征。Wang等[7]提出了一种利用嵌入KNN分类器来加速基于Wrapper的特征子集选择方法。该方法通过构造一个分类器距离矩阵来存储映射到所选特征上的实例之间的距离，从而加速基于Wrapper的特征选择。宋宝燕等[8]提出了一种基于Voronoi划分的位置数据KNN查询处理方法，通过R树确定查询点所在的Voronoi单元，进一步通过VHash获得KNN查询结果；在VHash、VR二级索引更新期间，针对变化的位置数据，实现了近似查询及精确查询。大多方法在计算两个样本距离时都认为每个特征的重要程度是相同的，但事实上，大多特征对类别的贡献度应不同。因此，本文使用加权K近邻（WeightedK-Nearest Neighbor，WKNN）计算距离。

进化计算（Evolutionary computation，EC）方法中的自适应机制引起了研究者的广泛关注[9]。一般而言，具有自适应机制的EC算法可以在迭代过程中自动调整算法的参数。特别是遗传算法，种群规模在遗传算法整个寻优过程中扮演着重要的角色，它规定了搜索样本的数目，交叉算子是生成新个体的主要方法，可以从全局搜索优良的个体，变异算子能够从局部搜索出发，使个体更加接近最优解，从而提高算法的局部搜索能力。通过自适应地调整遗传算法的参数，可以避免算法过早收敛和后处理速度慢。Koromyslova等[10]提出了一种自配置遗传算法（SCGA）。所有类型的遗传算子用相同的概率用于新的子代，通过评估遗传算子类型的适应度，对概率进行动态调整。自适应遗传算法（AGAs）[11]通过同时修改交叉值和变异值来确保种群多样性，从而为神经网络学习提供理想的初始权值。这一现象对于消除局部收敛和防止算法停滞是很重要的。

针对大多已有基于K近邻和遗传算法的特征选择方法中没有考虑各个特征的重要度不同，以及出现的过早收敛，特别是局部最优解问题，本文提出了一种基于自调优自适应遗传算法的WKNN特征选择方法，简记为WKNNSTA_GAFS（WeightedK-Nearest Neighbor Feature Selection Based on Self-Tuning Adaptive Genetic Algorithm）。该方法将WKNN和自调优自适应遗传算法结合起来，首先使用WKNN预测样本的类别，为每个特征分配一个权重来衡量特征的分类能力。在计算样本类别时既考虑了每个特征的不同分类能力，又考虑了最近邻的距离。然后利用自调优自适应遗传算法，对变异率、种群规模和收敛阈值进行参数调整，在迭代过程中搜索最优特征权重向量。不仅能克服局部最优解问题，还能消除过早收敛和防止由于参数调优反馈不稳定而产生的过高的计算成本。

1 自调优自适应遗传算法的WKNN特征选择方法

1.1 加权K近邻

传统的KNN方法中，预测样本类别时，使用相同权重的K个最近邻，即权值为1/K。但事实上不同近邻的重要性可能是不同的，两个样本越接近，类别可能越相同，对目标类别预测的影响越大。因此，应该根据K个近邻与预测样本之间的距离，为每个近邻分配相应的权值。距离越近，分配的权值越大。

在本文中，如果没有特殊说明，均假设处理回归任务。给定一个回归问题D=(F,X,Y)，F={f1,f2,…,f m}为特征集合，X={x1,x2,…,xn}为包含n个样本的数据集，Y={y1,y2,…,y n}为目标变量集合。给定一个特征权重向量ωf=(ωf1,ωf2,…,ωf m)，则特征加权后测试样本x i=(x i1,xi2,…,xi m)(1≤i≤n)的观测值可以用Hadamard积表示为：

使用特征加权后样本x i与x j的欧几里德距离公式为：

则基于距离和特征加权K近邻的样本xi的预测值Pi(ωf)为：

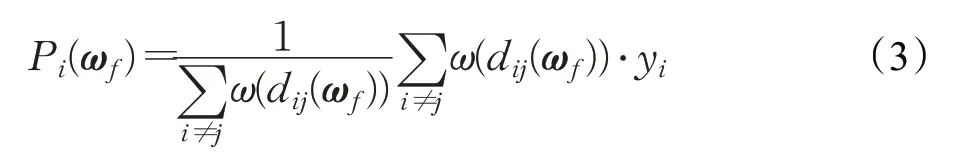
其中，j∈N Ki表示样本xi的K个近邻的指标集，即x j为x i的第j个近邻。

本文采用的距离加权函数定义为：

1.2 自调优自适应遗传算法

遗传算法是一类借鉴生物界自然选择和遗传机制的随机搜索算法[12-13]。传统的遗传算法在遗传进化的过程中采用固定参数，容易导致进化过程中出现过早收敛和停滞现象。因此，一种自调优自适应遗传算法（简称为STA_GA）被提出对遗传算法参数和收敛阈值进行自动调整，以提高收敛精度。

由于种群的多样性是保证遗传算法找到全局最优解的前提条件，因此，STA_GA算法的目的是通过对遗传算法参数的更新增加种群的多样性。在进化过程中，遗传算法的选择操作削弱了种群的多样性，交叉算子只有满足一定的条件才能保持种群的多样性，而变异操作则是保持种群多样性的有效算子[14]。种群规模越大也可以增加种群多样性，因此，本文提出方法将在遗传迭代过程中，对变异率、种群规模和收敛阈值三个参数进行自适应调整。

为了便于叙述，首先设在静态遗传算法中，Pm表示初始变异率，PS表示种群规模，Time表示迭代次数，cgen为当前代的迭代次数，θ表示收敛阈值。STA_GA采用传统的初始化策略，根据特征的数量和单个特征的组合，随机初始化每个粒子。

STA_GA将一个预定的候选评估数定义为收敛阈值，然后在自适应调整的过程中，判断当前代的静态迭代次数是否大于收敛阈值或者全局最优解是否更新，如果当前代的静态迭代次数大于收敛阈值，或者全局最优解始终没有得到更新，则对变异率、种群规模和收敛阈值三个参数进行重新调整。

变异率的更新公式为：

种群规模也会随之更新，更新公式为：

其中，gaiter表示静态迭代次数，即迭代过程中一代或几代连续没有获得更好最优解的个体总数。那么种群规模会增加这个个体总数的G倍。

如果当前静态迭代次数大于收敛阈值时，表示已经有超过收敛阈值个数的连续个体未更新最优解，本文中收敛阈值的初值为种群规模PS，即连续至少超出种群规模个体都未更新最优解，则种群规模会更新变大，因此，收敛阈值也应随之增加，本文中其增量为上一代种群规模，其更新公式为：

相比参数更新前，更新后的种群会包含更多个体，多样性也会更大，种群产生最优个体的概率也更高，有利于算法搜索到全局最优解。更新后的变异算子可以产生较多的新个体，种群多样性同样得到了提高，并且扩展了搜索空间，变异算子能够从局部搜索出发，使个体更加接近最优解，提高了算法的局部搜索能力，加快了遗传算法的收敛速度[15]。

仿真过程中发生收敛时，STA_GA进行参数更新，以便获得更高数量的候选种群和变异率，而不是在每次迭代中使用相同的遗传算子参数。当前代的静态迭代次数小于等于收敛阈值或全局最优解更新时，STA_GA采用静态的遗传算法参数设置。与静态的遗传参数设置相比，STA-GA参数调优机制的优点在于允许启发式搜索方法动态地在目标搜索空间中搜索全局最优解。

为了确保反馈的稳定，以及防止由于参数变化过大而导致的不一致的性能，限定了参数值的浮动范围，其中Pm小于等于0.5或者PS不能超过初始种群的三倍。对于每一代STA_GA，通过判断当前代的静态迭代次数是否大于收敛阈值或者全局最优解是否更新，对上述参数值进行重新评估。只有当满足停止条件时，自适应参数调优才会终止。

1.3 WKNNSTA_GAFS

WKNNSTA_GAFS算法主要包括初始种群、计算预测样本的类别、计算个体适应度、参数调优、执行遗传算子和最后得到最优权重向量六个部分。迭代结束后，对结果数组进行排序，得到全局最优特征权重向量ωbestf。通过对最优特征权重降序排序，依次选取对应的前N个特征组成一个子集。然后，利用分类器对其进行评价。

（1）初始化种群。使用[0，1]间的实数随机初始化含有m位基因的个体，种群中每个个体代表一个特征权重向量。

（2）适应度函数。种群初始化后，使用适应度函数计算每个个体的适应度值。第t个个体适应度函数定义为：

式中，Max是人为给出的使F t(ωf)≥0的正整数。C(ωf)为成本函数，表示为所有训练样本损失函数的平均值。成本函数越小说明整体的预测误差越小。成本函数定义为：

式中，L为损失函数，用预测值P i(ωf)与目标函数的真实值yi之间的差表示。本文损失函数定义为：

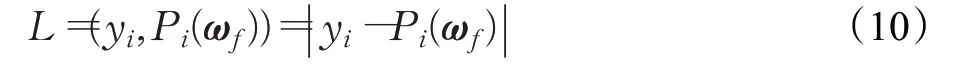
（3）STA_GA参数调优。通过判断，当本次迭代的静态迭代次数大于收敛阈值或全局最优解未更新时，开始进行参数调优。

（4）选择算子。选择是在个体适应度评价的基础上，从上一代中选择好的个体到下一代的操作。适应度值越高的个体被选择的概率越高。本文采用轮盘赌选择方法[16]。

（5）交叉算子。交叉操作是生成新个体的主要方法，决定了遗传算法的全局搜索能力。为了下一代能产生优秀的个体，本文采用算术交叉算子。首先根据概率随机选择一对父代个体P1、P2作为双亲，然后进行如下随机线性组合，产生两个新的子代个体P'1、P'2。

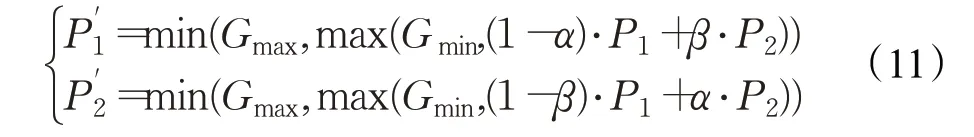
式中，α、β为（0,1)间的随机数，个体基因的取值范围为[Gmin,Gmax]。如果(1-α)⋅P1+β⋅P2的值小于Gmin（或大于Gmax），则P1'的值为Gmin（或Gmax）；P2'的值同理。

（6）变异算子。本文采用高斯变异算子，原因是它能重点搜索原个体附近的某个局部区域。它用符合均值为μ、方差为σ2的正态分布的一个随机数Q来替换原来的基因值。Q可由等式（12）求得：

式中，r i是在[0，1]范围内均匀分布的随机数，μ和σ的计算如下：

（7）停止标准。当变异率Pm大于最高变异率max_Pm或者种群规模PS超过初始种群的三倍时，算法停止。算法的流程如图1所示。

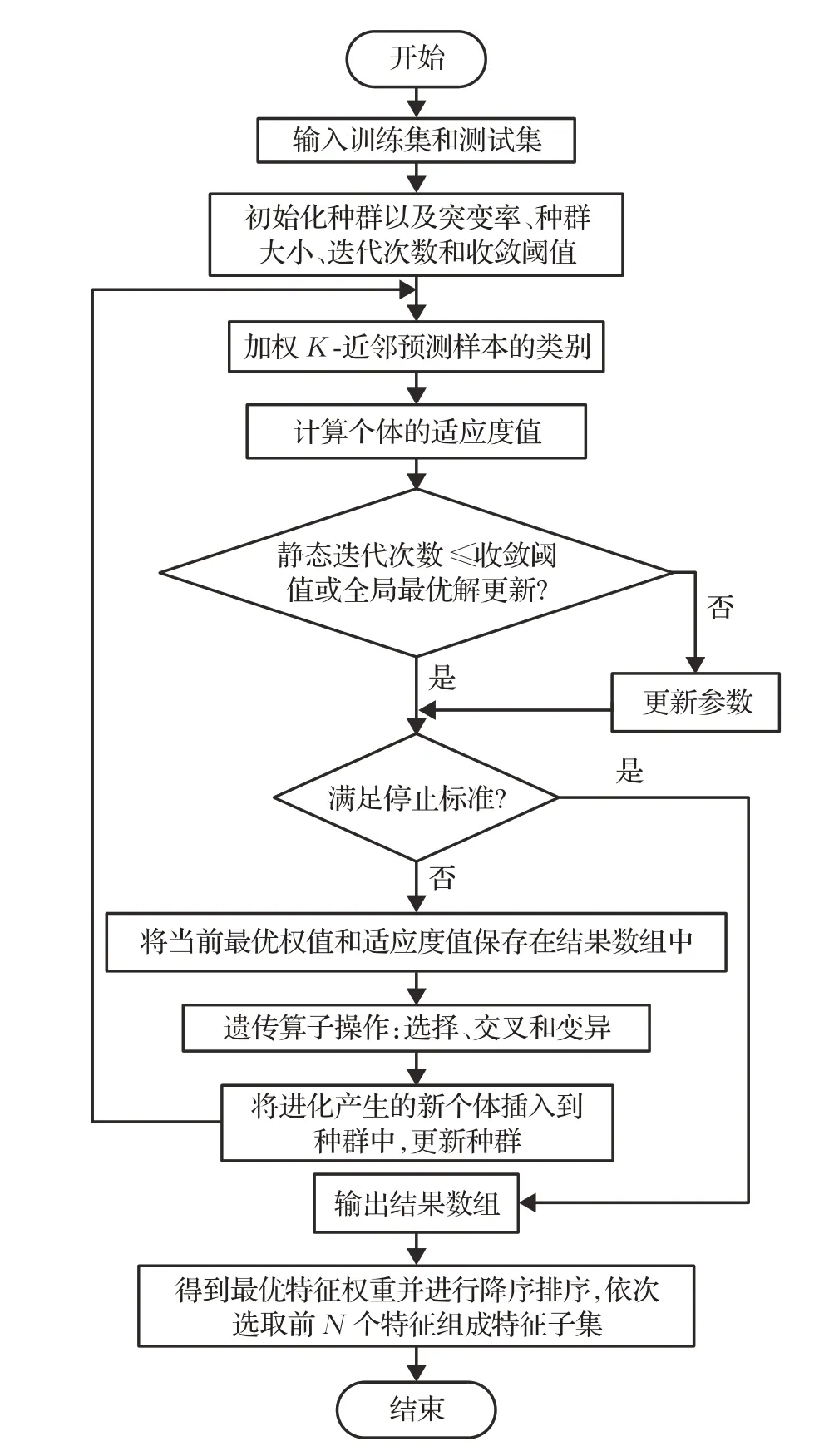
图1 WKNNSTA_GAFS算法流程Fig.1 Flow of WKNNSTA_GAFS

1.4 WKNNSTA_GAFS的收敛性分析

1.4.1 遗传算法收敛性定义

遗传算法的收敛性通常指算法所生成的迭代种群逐渐趋于某一稳定状态，或其适应值的最大或平均值迭代收敛于解的最优值。

设X t={x1(t),x2(t),…,x M(t)}为遗传算法的t代种群，x i(t)为t代种群中的第i个个体，i=1,2,…,M,M为种群规模。设Z t=max{f(xi(t)|i=1,2,…,M)}为种群中所包含的个体的适应度函数值的最大值，F∗=max{f(x)|x∈S}表示全局最优解，S为个体空间，x为S中的任意一个个体。则遗传算法的全局收敛性定义如下：

其中，P{Zt=F∗}表示第t代种群中的最优个体为全局最优的概率。

1.4.2 马尔科夫链定义

设随机序列X={X n,n=0,1,…}的离散空间为E,如果对于任意n≥0,以及i0,i1,…,i n,j∈E,满足条件概率：则称这类随机过程为离散马尔科夫链。马尔科夫链有无后效性的特点，即当前状态只与前一状态有关，而与其他状态无关。

1.4.3WKNNSTA_GAFS收敛性证明

将WKNNSTA_GAFS看作是一个离散状态下的随机序列，把每一代种群P(1),P(2),…看作是一种状态，种群的代代演化可以看作是状态之间的转移，当前种群的状态仅仅依赖于相邻的上一代种群，而与以往的种群状态无关。因此，可以利用马尔科夫链证明算法的收敛性。

假设总体状态空间为H，算法中每一代种群h(t)对应马尔科夫链中的一个状态，种群的逐代进化则对应马尔科夫模型中不同状态间的转移过程。标记每个h(i)∈H是否包含最优个体。由WKNNSTA_GAFS收敛性可知，一旦转移后的状态包含了当前最优个体，在以后的转移过程中将不断逼近包含最优个体的状态。最终即WKNNSTA_GAFS以概率1收敛到全局最优解。

1.4.4与WKNNSTA_GAFS算法收敛性能有关的参数

与算法收敛性有关的参数主要包括种群规模、交叉率和变异率。通常，种群规模太小，算法性能很差，甚至得不到问题的可行解；种群规模太大，尽管可以防止发生早熟收敛，但是计算量会增大，收敛速度缓慢。交叉率过大，容易使种群中高适应度值的个体被破坏掉，过小则会造成算法停滞不收敛；变异率过大容易使遗传算法成为随机搜索算法，过小则不会产生新个体。本文提出的WKNNSTA_GAFS采用自调优自适应遗传算法，自适应地调整算法变异率、种群规模和收敛阈值，在保证种群多样性得到提高的同时，加快了种群的进化速度，其收敛速度明显快于其他比较特征选择算法。

1.5 WKNNSTA_GAFS时间复杂度分析

传统遗传算法的时间复杂度为O(Max_Time×PS)，其中Max_Time为最大迭代次数；PS为种群规模。

WKNNSTA_GAFS算法的时间复杂度也是算法迭代次数Time和种群规模PS的函数。与传统遗传算法不同的是迭代次数和种群规模是不固定的，在迭代过程中是变化的。

WKNNSTA_GAFS算法的时间复杂度可表示为O(t0×PS0+t1×PS1+…+t n×PSn)，其中t i表示第i次参数更新与第i+1次参数更新之间迭代的次数，PS i表示相应的种群规模。

根据参数更新公式（5）～（7）可知，当迭代过程中连续至少超出种群规模个体都未更新最优解时，则种群规模会更新变大。因此，本文算法的时间复杂度也会高于传统遗传算法。

2 实验与性能分析

为了验证WKNNSTA_GAFS算法是否正确和有效，在5个数据集上，使用3种分类器，与其他7种特征选择算法进行比较实验。在实验中对所有数据集进行了归一化处理。

2.1 数据集

实验中使用数据集的简要描述如表1所示。其中，Z-Alizideh、Q_green、brain、TNCI来自UCI机器学习知识库[17]，Leukemia1下载自基因表达数据库。

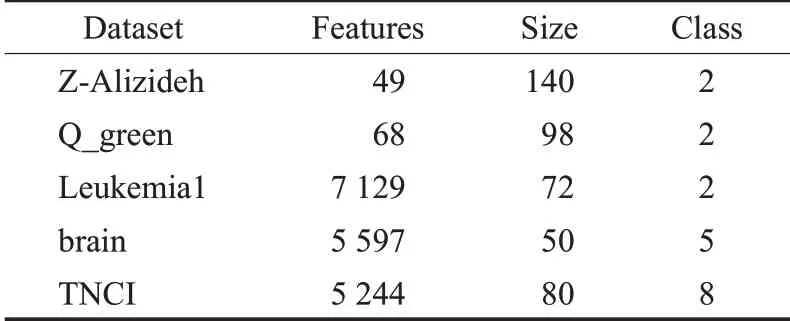
表1 数据集信息Table 1 Information of datasets

2.2 实验环境及参数设置

在Pycharm集成开发环境下进行实验。对每个数据集使用五重交叉检验，并与7种特征选择方法进行比较，包括生成子集的GAFS[12]、FCBF[18]和IG-GA[19]方法，以及排序的MIFS[20]、mRMR[21]、WKNNFS[22]和AGASVM[23]方法。使用KNN、支持向量机（Support Vector Machine）和随机森林（Random Forest）3种分类器进行分类预测。

在实验中，种群规模、迭代次数、收敛阈值等参数的初始值设置如表2所示。其中收敛阈值的初始值为初始种群规模PS，根据公式（7）收敛阈值的迭代公式可以看出，如果当前静态迭代次数大于收敛阈值时，表示已经有超过收敛阈值个数的连续个体未更新最优解，本文中收敛阈值的初值为种群规模PS，即连续至少超出种群规模个体都未更新最优解，则种群规模会更新变大，因此，收敛阈值也应随之增加，而收敛阈值越大也就意味着静态迭代次数更大时才会更新参数，因此需要的执行时间也会越长，但是算法的性能不一定会随之增大。为了确定初始的收敛阈值，本文在3个数据集上做了不同初始收敛阈值对算法性能影响的实验，实验结果如表3所示。从表3中可以看出初始收敛阈值不同，算法性能也不同，当初始收敛阈值为初始种群规模PS的值时，算法性能也最好，因此，本文选定种群规模PS的值为收敛阈值的初始值。

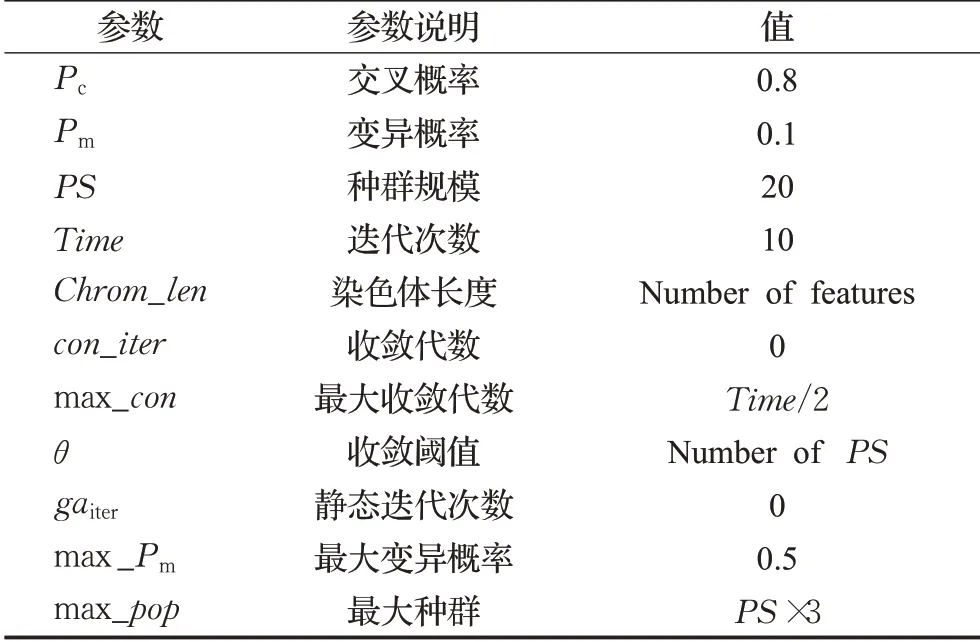
表2 算法的参数初始化选择Table 2 Algorithm parameter initialization selection

表3 不同初始收敛阈值对算法性能的影响Table 3 Influence of different initial convergence thresholds on algorithm performance

2.3 实验结果及性能分析

为了合理比较WKNNSTA_GAFS方法与GAFS、FCBF、IG-GA、MIFS、mRMR、WKNNFS和AGASVM特征选择方法的性能，进行了两组实验。首先，选择WKNNSTA_GAFS与MIFS、mRMR、WKNNFS和AGASVM四种排序特征选择方法获得的特征排序结果中相同个数的特征，分别使用上述3种分类器在5个数据集上进行分类预测，相应实验结果如图2所示，横坐标为排在前面的特征的个数(N)，纵坐标为选择前面N个特征后使用上述3分类器进行分类预测获得的准确率的平均值（mean F1 score）。

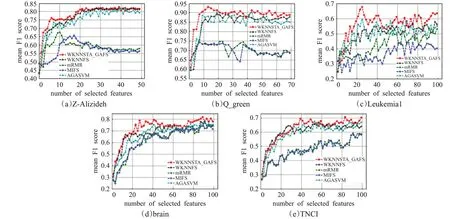
图2 WKNNSTA_GAFS、MIFS、mRMR、WKNNFS和AGASVM在5个数据集上的F1 score平均值比较Fig.2 Comparison of mean F1 score of WKNNSTA_GAFS，MIFS，mRMR，WKNNFS and AGASVM on 5 datasets

为了评价所提出算法的性能，计算了不同特征选择方法在不同数据集和不同分类器上获得的F1 score平均值以及标准差。实验结果如表4（Mean±std）所示。Mean表示每种算法获得最优分类性能的F1 score平均值，std表示标准差。其中Avg表示算法在给定数据集上使用KNN、SVM和RF三种分类器的F1 score平均值，表中黑体部分表示同一数据集中F1 score平均值最高。

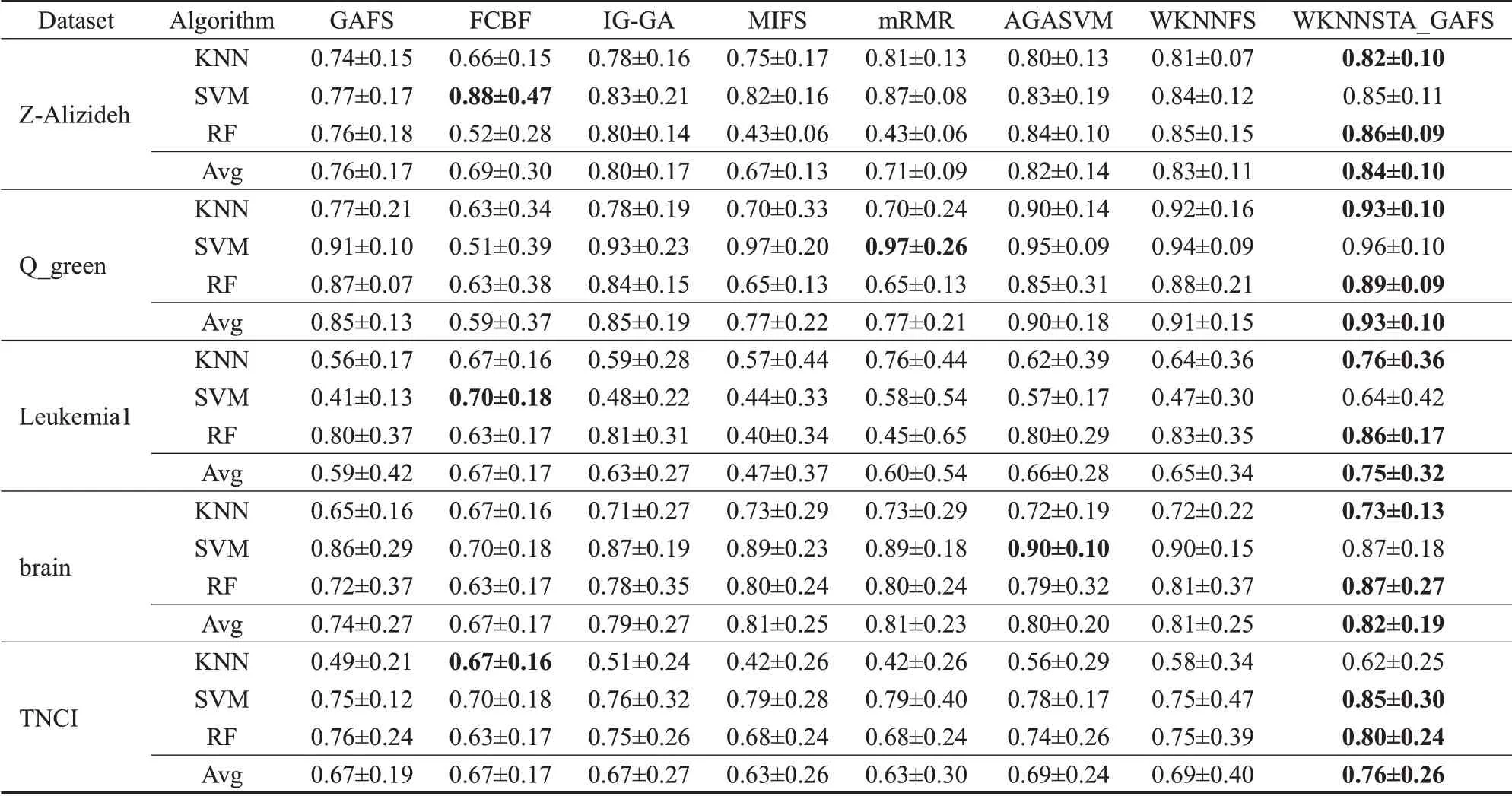
表4 各算法使用不同分类器在5个数据集上的均值和标准差Table 4 Mean and standard deviation of each algorithm by using different classifiers on 5 datasets

从表4可以看出，WKNNSTA_GAFS最优分类性能占比和F1 score平均值方面基本上都高于其他对比算法。在Z-Alizideh、Q_green、Leukemia1、brain和TNCI五个数据集上，WKNNSTA_GAFS与生成子集的方法比较，得到了更高的F1 score平均值。WKNNSTA_GAFS与FCBF相比，分别提高了15%、11%、8%、15%和9%；与GAFS相比，分别提高了8%、8%、16%、8%和9%；与IG-GA相比，分别提高了4%、8%、12%、3%和9%。其次，与排序方法的F1 score平均值进行比较，WKNNSTA_GAFS相比MIFS，分别提高了17%、16%、28%、1%和13%；与mRMR相比，分别提高了13%、16%、15%、1%和13%；与AGASVM相比，分别提高了2%、3%、9%、2%和7%；与WKNNFS相比，分别提高了1%、2%、10%、1%和7%。虽然在Z-Alizideh、Q_green和brain数据集上，WKNNSTA_GAFS与WKNNFS的F1 score平均值差异并不显著，但是WKNNSTA_GAFS的std更低，分类性能更加稳定。综上所述，WKNNSTA_GAFS方法优于其他FS方法。

3 结束语

本文提出了一种基于自调优自适应遗传算法的WKNN特征选择方法，该方法利用WKNN算法预测样本的类别，为每个特征分配一个权重来衡量特征的分类能力。在计算样本类别时既考虑了每个特征的不同分类能力，又考虑了最近邻样本的距离。并使用自调优自适应遗传算法搜索最优的特征权重向量。通过STA-GA的自适应参数调优机制对变异率、种群规模和收敛阈值进行调整，以获得理想的搜索空间，避免局部收敛；其次自定义停止标准，使参数调优反馈稳定，同时避免优化过早终止。在5个真实的数据集上，将该方法与现有的7种特征选择方法分别进行了对比实验。实验结果表明，该特征选择方法赋予重要的特征更高的权重，从而有效地提高了分类精度。在未来的工作，将努力进一步提高WKNNSTA_GAFS的分类精度，使用更多的分类器评估其应用潜力。