一种改进的Qtree_ORB算法

杨世强，白乐乐，赵 成，王国栋，李德信

西安理工大学 机械与精密仪器工程学院，西安 710048

同时定位与建图算法（Simultaneous Localization And Mapping，SLAM）是指移动机器人在没有任何先验环境的情况下同时完成自身的定位与周围环境地图的构建[1-2]。SLAM根据传感器的不同可以分为激光SLAM和视觉SLAM，虽然视觉SLAM相比于激光SLAM精度较差，但是由于其价格低廉得到了广泛的应用。

视觉SLAM根据利用图像信息的不同可以分为基于特征的SLAM方法和直接SLAM方法。基于特征的视觉SLAM方法是对每帧图像进行特征提取，并构建描述符，然后通过特征点的匹配来进行位姿和特征点三维坐标优化[3]。直接SLAM方法不需要进行特征提取，通过计算局部像素的梯度和方向值，优化出相机的位姿和三维点。基于特征的SLAM方法由于其对复杂场景鲁棒性高的优点得到了广泛的研究。

目前在视觉SLAM中由于ORB[4]（Oriented Fast and Rotated Brief）特征点速度快的优点而被广泛应用。ORB算法虽然有着较高的提取实时性，但是其提取的特征点不均匀，容易提取到过多重叠的特征点。Sun等人[5]提出了一种基于多探针LSH的A-ORB算法，虽然鲁棒性有一定的提高，但是提取的特征点较少，仍存在特征点分布不均匀，容易产生簇集的现象。

针对标准ORB算法分布不均匀的问题，Mur-Artal等人[6-7]所提出的ORB-SLAM算法中采用四叉树来对特征点进行均匀化处理，同时采用了自适应阈值的方法对ORB算法进行了改进，提高了算法的均匀度，但存在迭代次数多、过均匀的问题。在ORB-SLAM2的基础上还提出了很多优秀的SLAM系统，如Yu等人[8]提出的DS-SLAM，Bescos等人[9]提出的DynaSLAM算法，这些SLAM系统并没有对特征点提取模块进行改进，仍采用传统的四叉树结构来进行特征点的提取，特征点过均匀和迭代次数多的问题并没有得到改善，影响了SLAM系统的精度。伍锡如等人[10]提出一种改进的基于四叉树的ORB特征提取方法，但是仍采用传统的四叉树结构管理特征点，所提取的特征依然存在过均匀的问题。

针对ORB-SLAM2中过均匀、迭代次数过多的问题，本文以ORB-SLAM2为基础，提出了一种改进的Qtree_ORB算法。首先通过在图像金字塔层自适应划分网格提取特征点；然后对四叉树划分深度进行限制，设定特征点响应值的最小阈值；最后对本文所提出的方法进行均匀度和匹配性能的实验，并将该方法融合到ORB-SLAM2视觉里程计前端，并使用TUM中的RGBD数据集进行测试，实验表明，本文方法可以有效地改善ORB-SLAM2的性能。

1 ORB算法原理

ORB算法[4]分为特征点的提取和特征描述符计算两部分，分别是基于FAST[11]的oFAST（oriented FAST）特征点检测算法和基于BRIEF[12]的rBRIEF（rotated BRIEF）二进制特征描述符计算算法，有效解决了FAST特征点算法不具备旋转不变性的缺陷。

1.1 oFAST角点提取

如图1所示，FAST角点提取时通过检测以像素点p为圆心，以3为半径的圆上16个像素点与圆心p的灰度差来提取角点。如果圆周上有N个连续像素点的灰度值与圆心p的差大于某一阈值t，则将圆心像素点p作为候选特征点。其中N一般取12，称为FAST-12，常用的还有FAST-9、FAST-11。阈值一般为p点灰度值的20%。

图1 FAST角点提取图Fig.1 FAST feature point extraction diagram

针对FAST角点不具备旋转不变性和尺度不变性的缺点，ORB算法通过构建图像金字塔来实现尺度不变性，而特征的旋转不变性通过灰度质心法（Intensity Centroid）来实现。

灰度质心法主要用来给FAST特征点确定一个主方向，其主要步骤为：

（1）在特征点的局部图像块B中，定义图像块的矩为：

（2）通过B的矩找到图像块的质心：

（3）连接图像块的几何中心O与质心C得到方向向量OC，定义为特征点的主方向为：

1.2 rBRIEF描述子提取原理

BRIEF是一种二进制描述符，其构成了一个由0和1组成的描述向量，可以将此描述向量表述为：

其中，P(x)、P(y)是以特征点为中心的图像块，在x、y像素点处的灰度值。

选取M对测试点(x m,y m)就能产生一个二进制描述向量。二进制描述符可以表述为：

为了使BRIEF算法具有旋转不变性，rBRIEF算法通过对图像块中任意M对点(x m,y m)生成的m维二进制序列，定义一个2×m的矩阵S：

由特征点的主方向θ，确定旋转向量Rθ，对矩阵S进行旋转，可得到如下式的描述矩阵Sθ：

通过将描述矩阵旋转到主方向上，改进了BRIEF算法不具有旋转不变性的缺点。旋转后的BRIEF描述符可以表征为：

2 改进的Qtree_ORB算法

在ORB-SLAM2[6]中采用一种基于四叉树来提取ORB特征点的算法，称为Qtree_ORB算法。Qtree_ORB算法主要分为以下几个部分：（1）构造图像金字塔。通过构建出8层图像金字塔，为图像增加了尺度信息，解决了ORB算法中尺度不变性的问题。（2）对每一层图像金字塔进行网格划分。（3）用初始阈值iniTHFAST对每个网格进行FAST角点的提取，如果在网格内提取不到特征点则降低阈值用最小阈值minTHFAST来提取FAST角点。（4）基于四叉树均匀的选取所需要的FAST角点。首先初始化节点，得到初始的四叉树结构。其次划分节点，若节点中无特征点则删除该节点，若节点中的个数为1则不再划分节点，若节点中个数大于1则继续划分节点，若节点数大于期望的特征点数则不再进行划分节点。最后在每个节点中保留具有最高Harris响应值的特征点作为最终的特征点。以上标准的Qtree_ORB算法会存在所提取特征点过均匀和迭代次数多的问题，基于此本文对四叉树的划分深度、特征点的保留策略、金字塔网格的划分进行改进。

2.1 网格划分

在构造图像金字塔后对每层图像进行网格划分，原ORB-SLAM2算法中对每层图像根据工程经验值划分为30×30网格，不能很好地适应外部环境。所以本文对于网格划分采取自适应处理，根据每一层图像所需特征点数量采用面积法来对每一层图像进行网络划分。

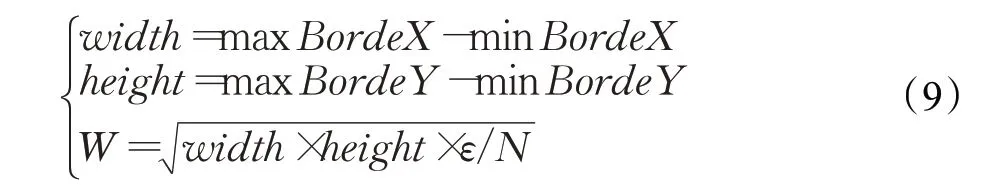
其中，maxBordeX、minBordeX、maxBordeY、minBordeY为每层图像的边界坐标，width为每层金字塔图像的宽，height为每层金字塔图像的高，ε为比例系数，经过实验验证ε值为1.8，N为所需的特征点数目。W为划分网格的宽与高，在不为整的情况下对其进行取整运算。

由每层图像金字塔的宽和高来计算出实际划分的行与列，在不为整的情况下进行向上取整运算，如下式：

其中，nCols为网格划分的列，nRows为网格划分的行。网格的实际宽和高为：

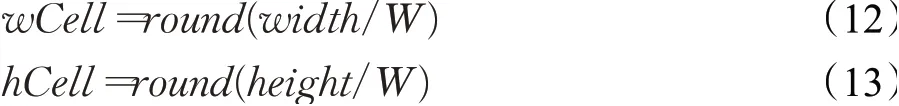
其中，wCell为划分网格的实际宽，hCell为划分网格的实际高，round为取整函数。

在划分网络后需要在每层上进行特征点的提取，每一层图像所提取的特征点数目为：

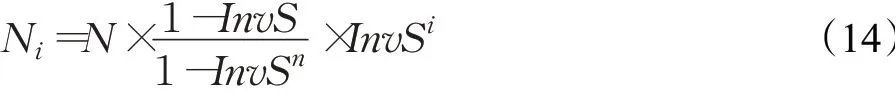
其中，N i每层所需要的特征点数目，InvS为每层图像缩放尺度因子的倒数。上式构造了一个等比数列，比例系数为InvS，其和为N，为所需要的总的特征点数目。

在网格内提取特征点时首先用初始阈值iniTHFAST对每个网格进行FAST角点得提取，如果在网格内提取不到特征点则降低阈值用最小阈值minTHFAST来提取FAST角点。最后采用非极大值抑制算法减少重叠特征点的输出。

2.2 划分四叉树

通过上述划分网格所提取的角点存在着大量的冗余，需要用四叉树来对其进行进一步的筛选。其主要思想是把具有ORB特征的图像分割为四叉树节点，然后根据Harris响应值保留节点中响应值最大的特征。

传统的四叉树划分在有些情况下会导致四叉树分割次数过多，降低算法效率，其次所提取到的特征点存在过均匀的问题，针对这些问题，本文对四叉树的划分重新进行限制，首先根据每层金字塔图像所需特征点数目来设定最大划分深度Dmax，四叉树划分深度间的关系可以表达为：

其中，d为四叉树当前划分深度，Dmax为最大划分深度。每层节点数量与划分深度的关系表达为：

其中，Nodes i当前划分深度下的节点数目。

如图2所示，在划分为四叉树节点之后是对四叉树节点中特征点的保留，首先对每个节点中的特征点数目进行判断，若该节点中没有特征点则删除该节点；若该节点中只有一个特征点，则保留该节点；若节点中有两个或者两个以上的特征点时，根据该节点中所有特征点的Harris响应值对其进行排序，保留节点中具有Harris响应值最高的特征点并删除掉其他的特征。最后对Harris响应值的最小值进行限定，若提取到的特征点的Harris响应值小于其最小的阈值，则不再提取该节点中的特征。图2中nNum为节点中的特征点，maxKP为Harris响应值最大的特征点，minH为Harris响应值的最小阈值。

图2 四叉树划分流程图Fig.2 Flow chart of quadtree division

2.3 特征点的匹配

在提取完特征点之后，需要进行特征点的匹配。特征点匹配是指两幅图像之间特征像素点的对应关系，从而确定两幅图像的位姿关系。在SLAM中通过特征匹配确定当前路标与之前观测到路标的对应关系，然后对机器人的位姿进行推测。本文所采取的特征点匹配方法如下：

（1）对两帧图像的特征点进行暴力匹配[13]（Brute-Force Matcher），得到两帧图像上的初始匹配的点对信息。

（2）暴力匹配后的点对存在着很多的误匹配，需要进一步的筛选。所以通过汉明距离来进行进一步的筛选，记所有匹配点对描述符间的最小距离为Dmin，当两个特征点间的汉明距离小于30与2×Dmin的最大值时，认为该点对为粗匹配点对。

（3）在完成粗匹配后利用随机抽样一致算法[14]（Random Sample Consensus，RANSAC）对粗匹配点对中的误匹配进行进一步的滤除，都得到最终的匹配点对。

通过以上步骤可以得到正确的匹配点对信息，为后续机器人的位姿计算提供了依据。

3 实验结果与分析

本文所有实验都是在一台处理器为i7-2600，内存8 GB，操作系统为Ubuntu14.04的台式计算机上运行，对实验中的数据均测试15次取平均值来避免实验的随机性。在第一个实验中对提取到的特征点均匀性、准确率和运行效率进行测试。在第二个实验中，把改进算法融入ORB-SLAM2中的视觉里程计中，测试改进算法的绝对轨迹误差（Absolute Trajectory Error，ATE）与相对轨迹误差（Relative Posture Error，RPE），并与标准ORBSLAM2进行比较，验证其应用在SLAM系统上的可行性。

经过多次实验测定，四叉树划分深度在图像金字塔第一层至第四层的最大划分深度取3，第五层至第六层的最大划分深度为2，第7层至第8层的最大划分深度为1。Harris响应值的最小阈值取18。这样一方面可以减少冗余计算提高速率，另一方面可以使特征点的均匀性更好。

3.1 特征点均匀度和匹配性能测试

本实验采用Mikolajczyk数据集[15]来进行均匀度和匹配性能的测试。实验中取每组数据集中前两张图像作为实验对象进行特征点的提取与匹配，分别对不同算法在模糊、视角变化、缩放、旋转、光照变化下进行性能测试并进行对比。

将改进的Qtree_ORB算法与基于四叉树的Qtree_ORB算法以及OpenCV 2.4.11中提供的传统ORB算法进行对比，所提取的特征点数目设置为1 000，其余均为默认参数。记本文改进的算法为Improved_Qtree_ORB，除本文设置的参数外，其余均为Qtree_ORB算法的原始参数值。

3.1.1 图像均匀度测试

用图像特征点的分布均匀性[15]来判别图像中的特征点是否分布均匀，对待检测的图像进行区域划分，把图像从竖直、水平、中心和四周、45°和135°进行划分。然后分别计算各个区域内的特征点数目，并将其构建为一个向量。计算特征点区域统计分布的标准差，将标准差定义为特征点分布的均匀度S。标准差越小表明特征点数量的波动越小，分布越均匀，反之则分布越不均匀。

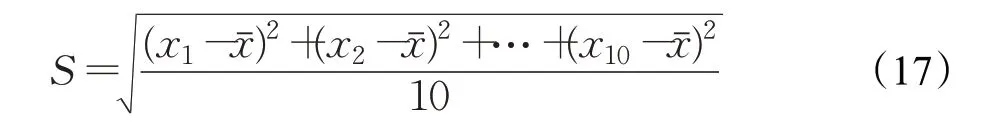
其中，x1,x2,…,x10分别为划分的10个区域内的特征点数量，为其平均值。

表1为三种算法在不同数据中的均匀度情况。传统ORB算法在提取到的特征点的均匀度最大，这是由于传统ORB算法所提取的特征点过于集中所导致的；Qtree_ORB算法所提取到的特征点的均匀度相比较传统ORB算法的均匀度有很大的提升；Improved_Qtree_ORB算法的均匀度最低，这是因为其对四叉树的划分深度进行了限制，在每个四叉树节点中提取的特征点的数量基本相同。Improved_Qtree_ORB的平均均匀度为38.74，相比于Qtree_ORB算法的65.98提升了41.3%。

表1 Mikolajczyk数据集特征点分布均匀度Table 1 Distribution uniformity of feature points in Mikolajczyk dataset

图3为三种算法的均匀度比较图，图4是三种算法在尺度变化数据集bark下所提取到的特征点。可以看出传统ORB算法所提取到的ORB特征点有簇集现象，分布并不均匀。Qtree_ORB算法所提取到的特征点虽然没有簇集现象，但是出现了过均匀的情况，在一些梯度变化不明显的地方也提取了一些Harris响应值较小的特征点。Improved_Qtree_ORB算法的均匀化效果最好。

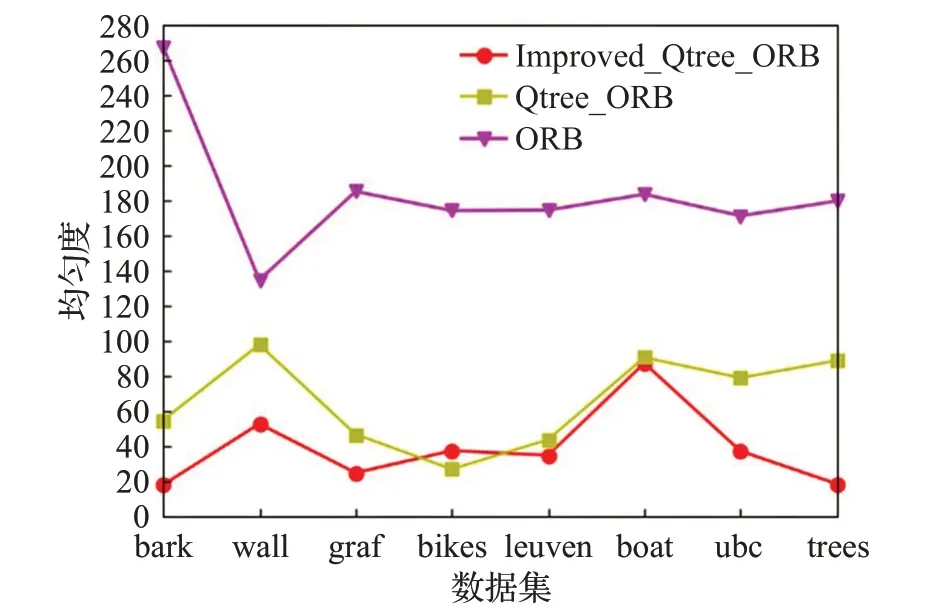
图3 特征点均匀度比较Fig.3 Comparison of feature point uniformity

图4 特征点提取比较Fig.4 Feature point extraction comparison

3.1.2 特征点的匹配测试

用特征点的匹配正确率C来评价两帧图像特征点匹配的准确度，定义为：

其中，mc为正确匹配点对，m为所有匹配点对。

图5为三种算法在不同数据下特征点匹配正确数量的对比图，图6为三种算法在不同数据下匹配正确率的对比。可以发现Improved_Qtree_ORB算法在匹配数量方面明显优于Qtree_ORB算法，但是比ORB算法略少一些。在匹配正确率方面，Improved_Qtree_ORB算法比Qtree_ORB算法在尺度变化数据集bark、视角变化数据集graf、光照变化数据集leuven、旋转变化数据集boat下有优势，Improved_Qtree_ORB算法与ORB算法准确率基本相当。从整体来看，Improved_Qtree_ORB算法更加稳定，整体优于其他两种算法。以下对三种算法在不同场景下的性能进行对比：

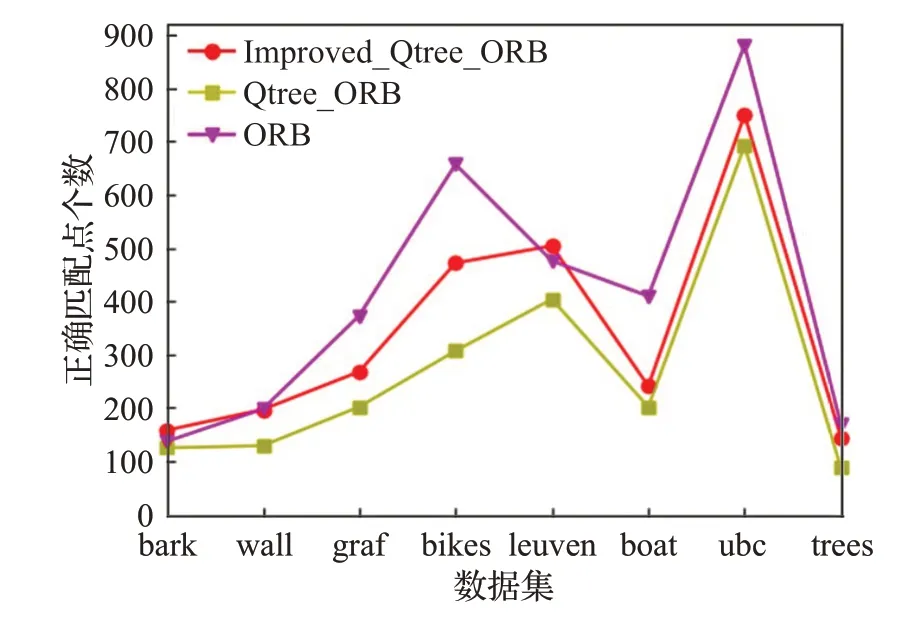
图5 特征点匹配正确个数对比Fig.5 Comparison of correct number of feature points matching

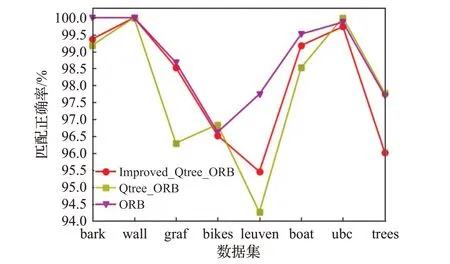
图6 特征点匹配正确率对比Fig.6 Comparison of matching accuracy of feature points

（1）尺度变化

图7（a）、（b）、（c）为三种算法在bark数据下经过RANSAC算法滤除误匹配后的匹配结果，表2为三种算法的匹配数量、正确匹配数量、准确率的实验数据。从表2中可以看出本文改进算法相比于其他两种算法所提取到的特征点的数目更多，其准确率三种算法基本保持一致。图7（a）中可以看出提取到的特征点集中在某一区域，因为尺度的变化从而导致两帧之间的特征点无法进行匹配，导致所参与匹配的特征点较少。Qtree_ORB算法因为保留了部分质量较差的特征点，所以参与匹配的特征点的数目也比较少。本文Improved_Qtree_ORB算法有效地改进了其他两种算法的缺陷。

图7 bark数据集的特征点匹配结果Fig.7 Feature point matching results of bark data

表2 尺度变化下各算法性能对比（bark）Table 2 Performance comparison of various algorithms under scale changes（bark）

（2）亮度变化

图8（a）、（b）、（c）为三种算法在leuven数据匹配结果，表3为三种算法在leuven数据下的实验数据。

图8 leuven数据的特征点匹配结果Fig.8 Feature point matching results of leuven data

在图8中明显可以看出ORB算法相比于其他两种算法在下方光线暗的地方无法提取到特征点，其特征点主要集中在光线较亮的区域。由表3可以看出Improved_Qtree_ORB算法的匹配数量明显多于其他两种算法，同时也保证了其匹配的正确率。Qtree_ORB算法匹配正确率较低的原因是其在提取特征点的过程中保留了一些质量差的特征点，比如地面的特征点从而最后影响了匹配正确率。

表3 亮度变化下各算法性能对比（leuven）Table 3 Performance comparison of algorithms under brightness changes（leuven）

在算法运行效率上，图9是三种算法的运行时间的比较，表4是具体的实验数据。由图9可以得出其ORB算法的效率最高，其次为Improved_Qtree_ORB算法，运行效率最慢的为Qtree_ORB算法。这是因为Qtree_ORB算法中添加了四叉树来管理特征点，其次对每层图像金字塔进行网络划分来提取FAST特征点。在进行四叉树划分时，每一次划分都要确定父节点中特征点的归属，同时由于没有限制其划分深度所以运行时间较长，本文通过对四叉树划分在不同图像金字塔层上限定划分深度，对图像金字塔进行自适应网格划分来提取特征点提高了其效率。

图9 运行时间比较Fig.9 Comparison of running time

表4 Mikolajczyk数据集特征点提取时间Table 4 Feature point extraction time of Mikolajczyk dataset ms

3.2 轨迹误差

在本实验中采用开源的SLAM系统ORB-SLAM2对本文改进算法进行测试，其评价标准为绝对轨迹误差（ATE）和相对轨迹误差（PRE）。ATE指的是相机位姿的真实值与SLAM系统估计值之间的差。该标准非常适合于评估视觉SLAM系统的性能。RPE用于计算相同两个时间戳上的位姿变化量的差，该标准适合于估计系统的漂移。

在实验中选择TUM[16]公共数据集用来评估室内动态场景下SLAM系统的精度和稳定性。因为ORBSLAM2系统中采用的是Qtree_ORB算法，因此本实验只用本文改进算法Improved_Qtree_ORB算法与其对比，不再与传统ORB算法进行对比。

图10中（a）、（c）为绝对轨迹误差图，其中红色线段代表误差，可以明显看出本文算法相对于Qtree_ORB算法的整体误差较小。图10中（b）、（d）为相对轨迹误差的波动情况，可以看出本文改进算法的相对轨迹误差的波动情况较小，有效地改善了SLAM系统的漂移程度。表5～表7分别为绝对轨迹误差和相对轨迹误差在SLAM系统中的测试值。从表5可以看出，改进算法在SLAM系统中有了很大改善。在绝对轨迹误差中均方根误差相比ORB-SLAM2降低了24.58%，标准差降低了44.6。

表5 绝对轨迹误差（ATE）Table 5 Absolute trajectory error（ATE）

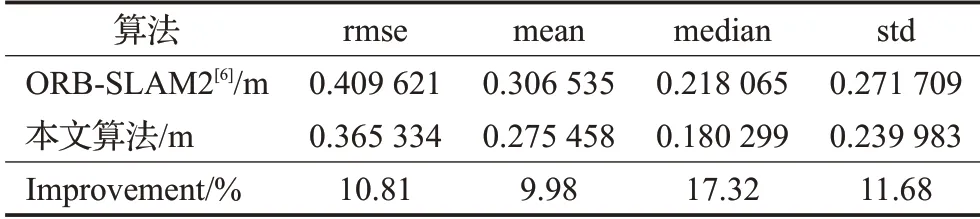
表6 相对位移轨迹误差（RPE）Talble 6 Relative displacement trajectory error（RPE）

表7 相对位旋转轨迹误差（RPE）Table 7 Relative position rotation track error（RPE）

图10 轨迹误差图Fig.10 Trajectory error grap

4 结语

本文提出了一种限制四叉树划分深度的Improved_Qtree_ORB算法。通过实验对本文改进算法的均匀度、匹配性能和在SLAM系统下的性能进行了测试。实验结果表明Improved_Qtree_ORB算法在均匀度方面性能优于ORB算法和Qtree_ORB算法，在保证高匹配正确率的情况下依然能够匹配足够多的特征点。通过在Mikolajczyk数据集下的测试，本文改进算法相比于其他两种算法其综合性能有明显提升。在SLAM系统测试中，其轨迹精度较优，在绝对轨迹误差中其均方根误差提高了24.58%；因此可看出本文改进算法的可靠性较高，可以运用在SLAM系统中。

尽管本文改进算法在SLAM系统中可靠性较高，但是也存在着一些不足之处。在未来可以通过提取亚像素特征点来提高ORB特征点精度，进一步提高SLAM系统的性能。