精英化岛屿种群引导的差分进化算法

钱峥远，曾国荪

1.同济大学 计算机科学及技术系，上海 201804

2.国家高性能计算机工程技术中心 同济分中心，上海 201804

差分进化（Differential Evolution，DE）算法通过模仿生物进化的过程在解空间内迭代搜索最优解，自从1997年由Storn和Price[1]提出以来，广泛应用于解决现实世界中的各类优化问题。差分进化算法作为一种竞争性的全局优化算法，具有所需控制参数较少，实现简单的优势。因此，差分进化算法及其改进算法常常被用于工业控制[2-3]、图像处理[4]、电力系统[5-6]、多模态函数求解[7]等领域。但是差分进化算法实际应用时易出现早熟收敛和搜索停滞的问题，且优化后期收敛速度慢。

针对上述问题，国内外学者进行了大量研究，研究认为出现早熟收敛的主要原因是控制参数的设置与进化策略的选择不当，使得种群过早地失去多样性[8]。而对于搜索停滞的问题，文献[9]认为它的发生原理还不明确，但是可以通过增加种群规模，降低其出现的概率。因此，差分进化算法的改进研究方向之一是对控制参数的改进，学者们提出人工设置多个控制参数数值，随机取用以提高种群多样性。例如Wang等[10]在CoDE算法中提出，对于每个个体从参数池中随机选择一组控制参数，而OXDE算法[11]则使用正交交叉概率代替传统概率参数。但是，这些控制参数的备选值是人工设置的，无法避免经验式的不稳定性。因此，学者们提出了随机参数设置方法和基于自适应的参数调节方式，例如Das等[12]提出让变异概率在0.5～1.0的范围内随机取值，或者在给定的时间间隔内线性减小。Brest等[13]提出了jDE算法，通过给每个个体分配不同的变异、交叉概率，并根据两个指定的阈值对其进行动态调整。此外，Wu等[14]提出的SACPMDE算法，Noman等[15]提出的aDE算法也是有效的参数自适应改进差分进化算法。研究方向之二是改进差分策略，例如Zhang等[16]在JADE算法中提出了一种基于外部的备份与历史信息结合的DE/currentto-pbest/1的差分策略，在SaDE算法中则提出每次变异时，由算法从多种变异策略中自适应地选择一种适合的策略执行[17]。研究方向之三是针对DE算法的种群结构进行改进，其中比较经典的有主从模型[18]、岛屿模型[19]和元胞模型[20]等。

但是，单一地对控制参数、变异策略或者种群结构进行改进，提升效果有限。因此，研究人员提出了综合改进算法，例如Kushida等[19]在iDE算法中尝试通过将种群分割成大小不等的岛屿，并给岛屿分配不同的控制参数，以便平衡全局搜索与局部搜索能力，同时通过个体迁移的方式进行岛屿间的基因交流，以便保持种群的多样性。但是，该算法仍存在一些问题：（1）由于算法中各岛屿的控制参数都是人工确定的，对不同问题的适应能力不足，同时种群初始化的随机性可能导致岛屿适应度情况与参数设置不匹配，影响算法稳定性。（2）各岛屿间的移民过程中，iDE算法选取的是各岛屿上适应度最佳的个体，这样做虽然有利于这些个体在各岛屿间扩散其基因，但在迭代后期，可能造成各岛屿上的基因趋同，种群多样性不足导致收敛停滞的问题。（3）iDE算法的个体迁移机制，虽然能增强当前最佳岛屿的搜索能力，但是没有考虑到增强局部搜索的位置，同时迁入适应度较差的个体也会干扰最佳岛屿的变异方向。

因此，为了提高差分进化算法的优化精度与收敛速率，避免“早熟收敛”和“搜索停滞”等问题，本文基于传统岛屿模型，研究一种精英化岛屿种群的差分进化算法（Elitist Island-based Differential Evolution，EIDE）。该算法在进化前期减缓最佳个体的基因扩散速度，保留种群的多样性，有效避免算法出现“早熟收敛”问题，同时加速对解空间的全局搜索，使得个体尽快接近全局最优解。算法在进化后期增强对适应度较高的个体周围空间的搜索，提高算法收敛精度，控制岛屿基因流向，维护个体多样性防止出现“搜索停滞”的问题。

1 传统的岛屿模型差分进化算法

本文基于文献[19]提出的岛屿模型差分进化算法（iDE）进行改进，其主要步骤包括：种群初始化及种群划分，迭代执行的变异、交叉、选择、移民以及个体迁移操作，这些操作是改进算法的基础。

1.1 种群初始化及种群划分

iDE算法和DE算法同样采用实数编码方式，首先随机生成NP个D维初始个体，对于种群中的第g代，第p个个体如公式（1）所示，其中均是一个实数，表示个体x p对应维度的数值，且取值范围为；各维度初始化如公式（2）所示，其中和分别是被选择个体x p的第q个维度值的上限和下限，表示一个取值范围在[0，1]的随机数。完成个体初始化后，iDE算法采用随机种群划分方式，将全种群P平均地划分为多个子种群（岛屿）P s(s=1,2,…,K)，其中K表示岛屿数量，全种群中的NPtotal个个体则随机地划分到各岛屿，每个岛屿包含NPtotal/K个个体。

1.2 进化操作

1.2.1 变异操作

变异操作是由种群中多个单独个体进行线性运算得到变异个体的过程，如公式（3）所示，其中X p(g)表示第g代的原始种群中的第p个个体，V p(g)表示第g代变异种群中的第p个个体，p1、p2、p3是原始种群里的三个个体，且p1≠p2≠p3。F是变异算子，可根据应用场景修改，F决定种群个体差分步长的大小。F的值较小会使得种群成员之间的差异性较小，使得算法容易出现局部最优的问题；F增大可以增强算法的全局搜索能力，增大搜索到全局最优解的概率，但会降低算法的收敛速度。

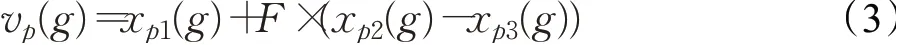
1.2.2 交叉操作

交叉操作将原始种群中个体的部分维度的值，与变异个体的对应维度的值按照某种规则进行交换，通过交换个体间某个分量以提高种群多样性。交叉操作生成交叉个体，如公式（4）所示，其中，r是区间[0，1]的随机数，t是区间[1,D]的随机整数表示第g次迭代中，第p个交叉个体的第q个维度。表示第g次迭代中，第p个变异个体的第q个维度。表示第g次迭代中，原始种群中的第p个个体的第q个维度值。CR是交叉概率，且，CR越大，交叉个体从变异个体中获取的值越多，更接近变异个体，全局搜索能力越强，但是收敛速度慢；反之，CR越小，其全局搜索能力就较弱，容易出现早熟的情况。iDE对于不同岛屿设置了不同的F算子及CR算子数值，以实现岛屿的分工，例如在岛屿个数为5时，文献[19]建议F与CR设置如表1所示。

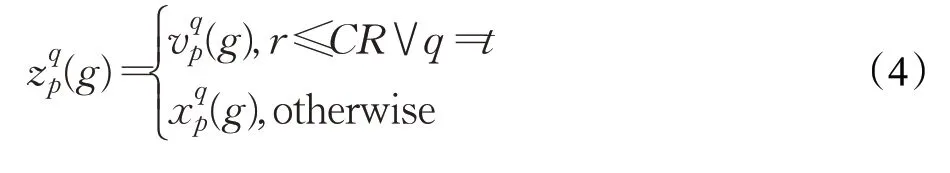
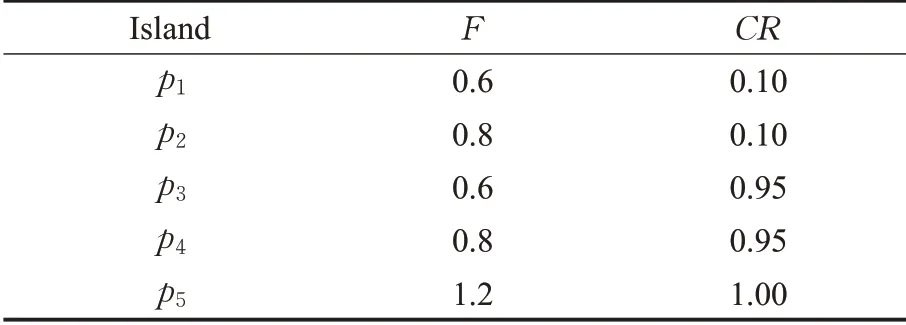
表1 iDE算法各岛屿控制参数设置Table 1 Control parameter settings of each island in iDE algorithm

1.2.3 选择操作

iDE采用贪婪的方式来选择进入下一代种群的个体，如公式（5）所示，其中f(x p)表示个体x p对应的目标函数值，x p(g)表示第g代种群中的第p个个体，z p(g)表示第g代的交叉种群中的第p个个体，x p(g+1)表示第g+1代种群中的第p个个体。

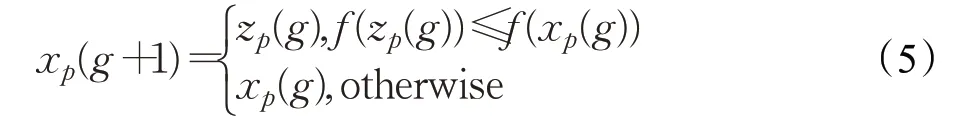
1.3 移民操作与个体迁移操作

iDE的移民和个体迁移周期为I，每隔I次迭代，将所有岛屿随机地连接成一个环，如图1（a）左半部分所示，岛屿作为环的节点，将它们以随机的顺序连接起来。而后在每个岛屿上选择适应度值最小的N P×R（R为移民比例）个个体，按照刚才随机确定的连接顺序，以顺时针的方向，从上一个岛屿移入下一个岛屿，如图1（a）中右半部分所示。iDE的个体迁移则是计算每个岛屿在这I次迭代中最佳个体适应度的平均值，以此平均值为标准，选出最佳岛屿（最佳个体适应度均值最小）和最差岛屿（最佳个体适应度均值最大）。将最差岛屿上的任一个体，复制到最佳岛屿上，而后将其在最差岛屿上删除，移民及个体迁移操作如图1（b）所示，虚线圈为最差岛屿上删除的个体，而绿色圆为其在最佳岛屿上的复制。

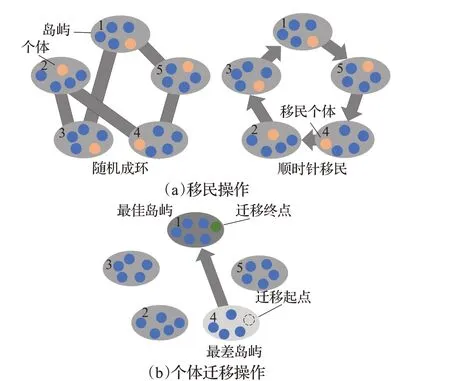
图1 iDE算法移民与个体迁移操作图Fig.1 iDE algorithm migration and individual transfer operation diagram

2 基于精英化岛屿种群的差分进化（EIDE）算法

针对iDE算法存在的问题，本文从岛屿分类、变异策略的选择、控制参数的自适应化、“移民”方向的控制、“个体迁移”对象的选择等多个角度，对iDE算法进行综合改进，使得新算法能够自主调整局部搜索能力与全局搜索能力。在此基础上新算法明确岛屿分工，利用精英化的思想来实现快速收敛到最优解的目的，同时利用岛屿间的基因隔离实现在迭代过程中保持种群多样性的目的。

2.1 自适应的精英岛屿选择

通常，精英个体被定义为种群中适应度值较好的个体，精英化则是通过精英个体对整个种群的进化起到引导作用。精英化思想常用在遗传、协同进化等进化算法中，取得了不错的效果。而在岛屿模型的差分进化算法中，精英个体分散在不同的岛屿上，虽然精英个体可以对该岛屿上的其他个体进化产生引导作用，但在迭代初期其他个体适应度较差的情况下进行变异操作，精英个体的子代适应度值减小的概率较小，将减慢收敛速度；在迭代后期，精英个体分散也易造成该岛屿上的其他个体与精英个体过度相似，导致种群失去基因多样性；同时由于精英个体适应度值较小，在其周围空间搜索得到全局最优解的概率较大。

因此，本文设计一种新的岛屿分类方法，使得不同类型的岛屿实现不同的功能，普通岛屿维持种群多样性，精英岛屿将精英个体集中在小范围并增强局部搜索以提升优化精度与收敛速率。此外，岛屿分类是实现有向移民策略的基础。为了便于叙述，本文均假设要优化一个极小值问题的解，假设算法初始化有K个岛屿，第k个岛屿初始化有N k个个体，则对于岛屿类型的判定方式如公式（6）、（7）所示，其中fitness()表示适应度计算函数，表示第k个岛屿第n个个体，bestFitness k表示第k个岛屿的最佳适应度值，表示所有岛屿最佳适应度值的均值，typek表示第k个岛屿类型函数，其值为1代表作为精英岛屿，其值为0代表作为普通岛屿。

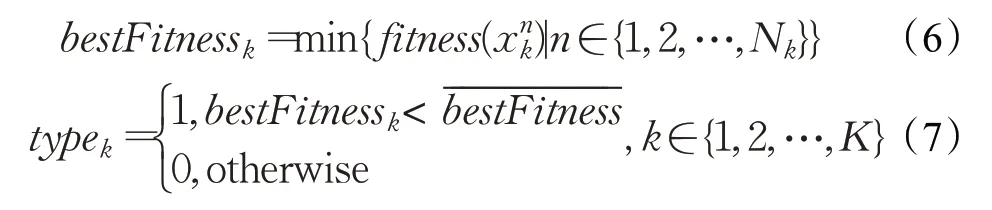
2.2 精英岛屿的进化操作

2.2.1 精英岛屿的变异策略

如2.1节中所述，EIDE算法将精英个体集中在精英岛屿，以期实现在适应度值较小的个体周围密集搜索，增大搜索到最优解的概率，并设计以普通岛屿维护种群多样性。对于普通岛屿采取DE/rand/1/bin的变异策略，并设置较大的变异概率及交叉概率值以增大普通岛屿的种群多样性。对于精英岛屿，则需要增强局部搜索能力，故本文选用文献[14]中的一种方向增强的变异策略。其主要思想为，选择适应度值最小的个体作为变异的基础个体，并向着适应度值次小的个体方向进化，如公式（8）所示，对于变异时的三个随机选择的个体，按照适应度函数值升序排序后存储。假设适应度值最小那个个体是，次小的是，最大的是。为了加速收敛，基础向量选择，并且由生成差分向量。

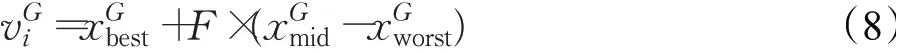
在精英岛屿上应用该变异策略的优势在于，精英岛屿上的个体变异时将会探索最佳个体的周围空间，且探索的方向都会在的上，即对于选定的变异个体，其变异过程不再是随机的，而是一个确定的过程。但是由于变异时所选用的个体还是在该岛屿的所有个体中随机选取的，所以整个变异操作还是一个随机的过程，可以保持算法搜寻全局最优解的能力。因此，应用该变异策略可实现增强精英岛屿的局部搜索能力的目的。

2.2.2 控制参数自适应方法

EIDE算法设计精英岛屿的主要目的是加速寻找最优解，但是由于差分进化算法本身的随机性，迭代时个体适应度的变化情况无法预测，参与变异过程的个体也无法确定，因此盲目地使用增强局部搜索的控制参数，极有可能使算法陷入局部最优。针对这个问题，EIDE算法设计通过控制参数的自适应，实现根据个体适应度情况，平衡其局部搜索与全局搜索能力。

精英岛屿自适应调整变异概率的方法如公式（9）所示，自适应调整交叉概率的方法如公式（10）所示，其中fbest、fmid、fworst分别是、和三个个体的适应度函数值，Fi表示第i个个体变异时的变异概率，Fl表示变异概率的下限，Fu表示变异概率的上限，CRl表示交叉概率的下限，CRu表示交叉概率的上限，f i表示第i个变异个体的适应度函数值表示该岛屿所有个体的平均适应度函数值，fmin和fmax分别表示当前岛屿种群中最好和最差个体的适应度函数值。

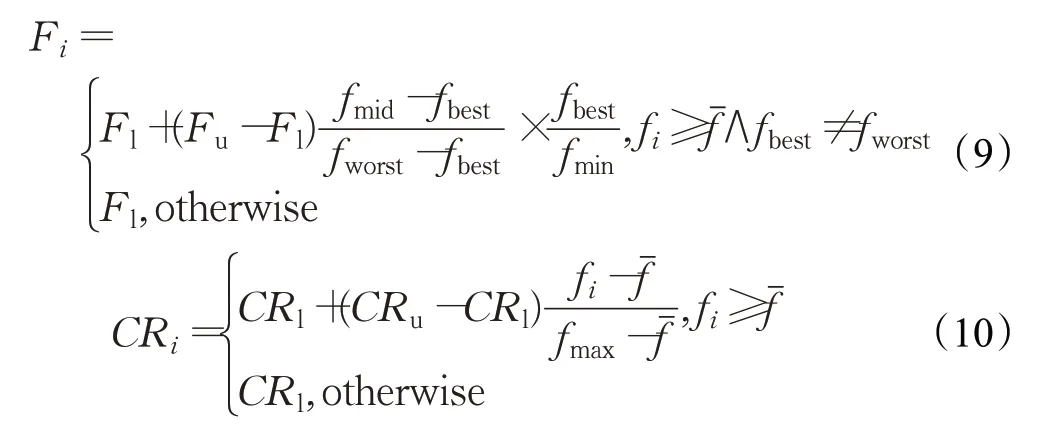
2.3 基于精英岛屿的有向“移民”操作

传统的岛屿模型，在搜索得到一个适应度较小的个体后，该个体的基因首先会在自己的岛屿内扩散，然后会随着“移民”过程，依次进入下一个岛屿，并在岛屿内扩散，然后再进入下一个岛屿，这就可能导致所有岛屿基因趋同，而陷入局部最优的情况。为了保证普通岛屿内的基因多样性，防止陷入局部最优解，EIDE算法设计所有岛屿都将自己的优质基因输入到精英岛屿中的最佳岛屿（适应度值最小的个体所在的岛屿），而最佳岛屿则只会将优质基因扩散到精英岛屿中，如图2（a）所示，将蓝色箭头终点的个体替换为箭头起点个体。

在EIDE算法设计的“移民”策略中，除了最佳岛屿以外的所有岛屿，用本岛屿内最佳个体（适应度值最小的个体），替换掉最佳岛屿上任一非最佳个体，而最佳岛屿将会为每一个精英岛屿，选择一个本次移民过程中未被替换过的个体（可能是最佳个体），用来替换掉精英岛屿上任一个体，且这个被替换个体不能是该岛屿的最佳个体。对于适应度较差的岛屿，只存在基因输出，而不存在基因输入，使得算法在迭代后期仍能保证种群中的基因多样性，防止陷入局部最优解。

2.4 精英增强的“个体迁移”操作

对于最佳个体的适应度值较大的岛屿，虽然也有可能在该岛屿上发现全局最优解，但这个可能性较低，而对于最佳个体的适应度值较小的岛屿，其发现全局最优解的可能性较高，因此EIDE算法增强在适应度值较小的个体周围的搜索，并增大适应度值较大个体与其子代个体的距离，在迭代过程中加入了个体迁移的机制，即将最差岛屿（岛屿内的最佳个体适应度值，在所有岛屿中是最大的）上的最差个体杀死，在最佳岛屿上复制一个最佳岛屿的最佳个体，如图2（b）所示，其中黑色虚线圈表示最差岛屿上删除的个体，黄色虚线圈表示最佳岛屿上最佳个体的复制个体，结合删除与复制操作，即实现了个体由最差岛屿向最佳岛屿的迁移。

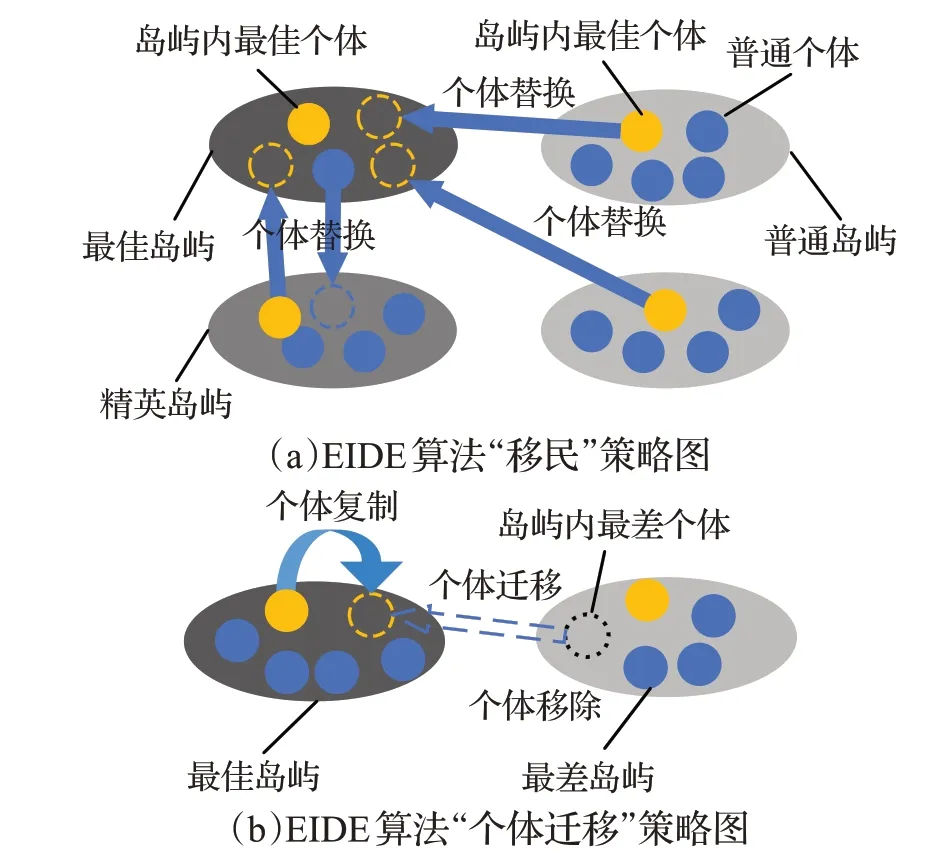
图2 EIDE“移民”与“个体迁移”策略图Fig.2“Migration”and“Individual Transfer”strategy diagrams of EIDE

EIDE算法每隔I次的迭代后，执行一次“移民”和“个体迁移”的判断，判断内容为最大岛屿接收的迁移个体总数，是否超过可接收的最大迁移个体数量。可接收的最大迁移个体数量随迭代次数递增，如公式（11）和（12）所示，其中K表示岛屿数量，Ntotal表示个体总数，R表示个体迁移比例，Nbest表示当前最佳岛屿的个体数量，g表示当前迭代次数，G表示最大迭代上限，trans ferNum代表岛屿可接收的最大迁移个体数量，flag表示是否可迁移标志。

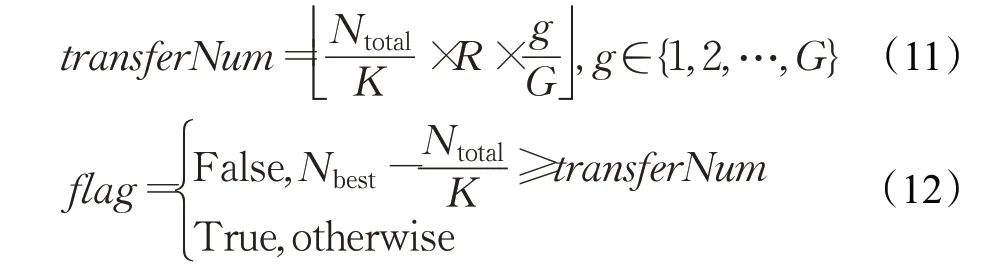
由于岛屿模型的并发性，各个岛屿可以并行进化。但如果“移民”和“个体迁移”发生得过于频繁，会严重影响算法的可并发性，增大执行时间，同时过于频繁的基因交流也不利于对基因的有效搜索；如果基因交流和个体迁移发生的频率过低，则会影响岛屿种群多样性的扩散和搜索优势方向的能力，因此每隔I次迭代执行一次判断，可平衡岛屿模型执行时间与优化能力。通过可迁移数量随着迭代次数递增的方式，实现迭代初期加强全局搜索，迭代后期加强在候选最优解周围搜索的目的，这符合差分进化算法迭代初期最优解方向并不明确的特点以及迭代后期加速收敛的需求。

2.5 EIDE算法描述

综合2.1～2.4节所述，EIDE算法的步骤为，首先初始化各岛屿种群（默认初始时所有岛屿均为普通岛屿）；然后进行迭代过程，包括各个岛屿分别执行变异操作、交叉操作、选择操作，在分类岛屿，而后执行“移民”“个体迁移”操作；重复迭代直至达到收敛条件或最大迭代次数，其伪代码描述如下：

算法1一种精英化岛屿种群的差分进化算法（EIDE）

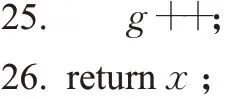
3 实验分析

为了验证EIDE算法的优化与收敛能力，本文在PC机开展实验，配置为IntelⓇCoreTMi7-8550U处理器和Window10操作系统，用Python3.6实现了EIDE算法和DADE、iDE、jDE、aDE算法[13，15，18，21]，并选取多个标准测试函数，分别利用上述5种差分进化算法求解每个测试函数的最小值，通过比较各个算法得到的解和实际值的误差，判断算法的准确度，并根据各个算法成功收敛所用的迭代次数，判断算法的收敛速率。

3.1 EIDE算法参数设置

实验中由于EIDE算法主要通过普通岛屿保持种群多样性，通过精英岛屿加强候选最优解附近的搜索，故普通岛屿变异、交叉概率设置分别为F=0.5,CR=0.9；精英岛屿变异、交叉概率上下限设置为Fl=0.1,Fu=0.4,CRl=0.1,CRu=0.6。由于EIDE算法的总时间复杂度为O(N⋅(N P+M)⋅D⋅T)，文献[22]的实验结果可发现多种群的改进DE算法，在种群数量较少，且子种群个体数量与标准DE种群个体数量相等时，两者执行时间差距较小。故保证EIDE算法的岛屿个体数量最大值≤DE算法的种群个体数量时，基本可以保证两者运算时间相近。因此，实验时，EIDE算法的每个岛屿种群个体数量NP设置为80个，“移民”与“个体迁移”判断的间隔代数I设置为5代，个体迁移比例R设置为20%，而其他4种算法的种群大小则为100，由于迁移个体数最大为NP×(1+R)故而可以保证在整个迭代过程中，EIDE的最大岛屿个体数均小于其他算法的种群个体数。EIDE的岛屿个数设置为5个，普通岛屿的变异概率和交叉概率参照文献[1]分别设置为0.5和0.9。精英岛屿的变异概率和交叉概率上下界如2.2节中所述。作为对照，DE算法的变异概率和交叉概率也分别设置为0.5和0.9。iDE、jDE、aDE、DADE、NEA/NC 5种算法的参数设置如其来源文献[13，15，19，21，23]中所述。所有算法的最大迭代次数为3 000次，均独立执行30次。

3.2 基准测试函数

为了测试算法性能，本文从文献[24-25]选取了9个标准测试函数，具体如表2所示，目标是求解它们的最小值，其中f1～f4为单峰函数，f5是有一个极值但不连续的函数，f6～f9为多峰函数，其维数均为D=30。

表2 基准测试函数Table 2 Benchmark functions

3.3 实验结果与分析

3.3.1 算法收敛精度分析

对于5种算法在9个标准测试函数下30次独立执行的优化结果的平均值和标准差如表3所示，各算法在各标准测试函数下，成功收敛的比例(SR)和多次运行下每代最佳适应度值的均值成功收敛时的最小迭代次数(MG)如表4所示。本文中认为成功收敛的条件是这次迭代的最佳适应度值与测试函数最小值误差小于等于一个阈值R，对于测试函数f2，阈值为10-2；对于测试函数f4，阈值为10-5；对于测试函数f7，阈值为10-1；对于测试函数f8、f9，阈值为1；对于其他5个测试函数阈值为10-8。而表格中的N/A表示此算法在此测试函数上多次重复运行的适应度均值未成功收敛。

表3 各算法在不同测试函数上优化精度对比Table 3 Precision comparison of solutions optimized by each algorithm on different test functions

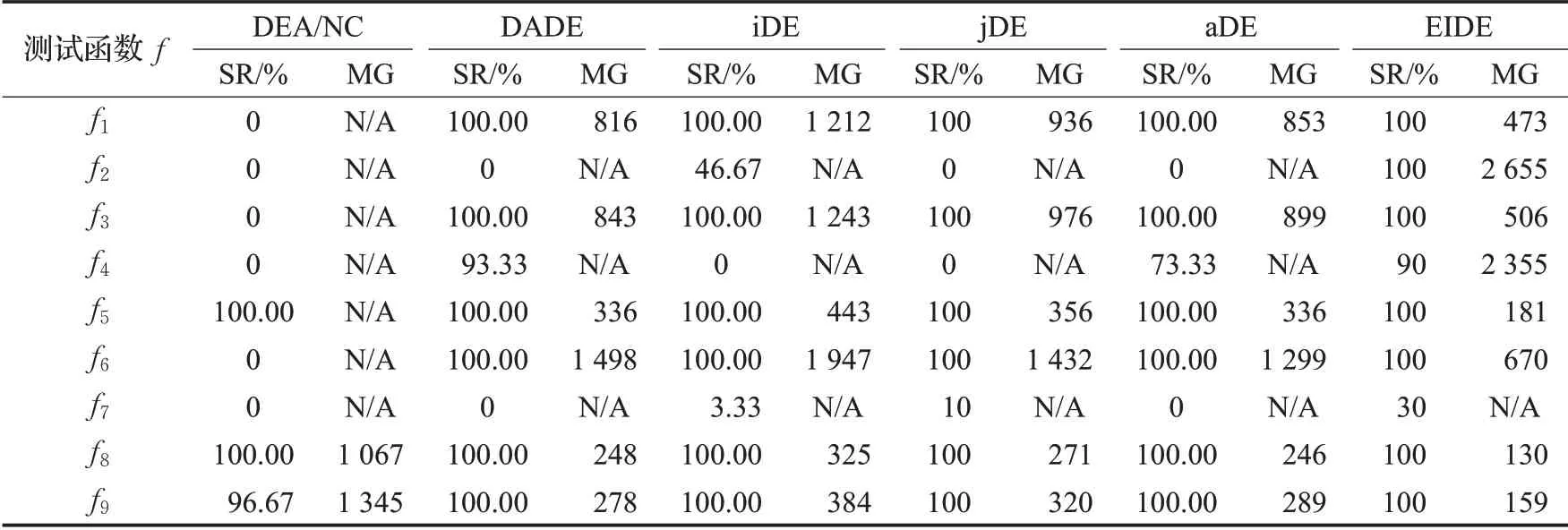
表4 各算法在不同测试函数上的收敛能力对比Table 4 Comparison of convergence ability of each algorithm on different test functions

SR的计算公式如公式（13）所示，MG的计算公式如（14）所示，其中T s表示多次重复运行中成功收敛的次数；T a表示重复运行的总次数；min(A)表示集合A中的最小元素；f b(i,k)表示第i次重复运行的第k次迭代的全种群（所有岛屿）的最佳适应度值；T表示该测试函数的目标解；R表示该测试函数的成功收敛阈值。

如表3所示，EIDE算法优化精度高。EIDE在9个测试函数中的7个上平均误差最小，特别是在单峰函数上，在f1和f3上EIDE的优化精度较其他算法准确1030以上。这是因为精英岛屿自适应得到的较小的变异概率和交叉概率，在迭代后期保证了收敛精度，普通岛屿较大的变异概率和交叉概率，维持着种群多样性，在收敛后期，通过“移民”策略保证精英岛屿继续进化。在f2上表现不佳的原因在于F和CR的自适应算法对于各维度权重不同的情况难以适应，因此可以看到同样采用参数自适应方法的jDE和aDE算法表现也是较差的。而DEA/NC算法放弃了交叉操作，并通过模拟退火的变异操作跳出局部最优，但单峰函数只有一个优化方向，因此在单峰函数上结果明显较差。在多峰函数上，EIDE算法的优势没有那么明显，主要是因为多个岛屿可能会收敛至不同极值，对最佳岛屿的进化方向形成干扰，但仍可以看出EIDE算法在4个多峰函数的3个上优化精度最高。

3.3.2 算法收敛速度分析

如表4所示，EIDE算法稳定，收敛成功率高。EIDE在9个测试函数中的7个上收敛成功率最高，因为普通岛屿的存在，保证了种群多样性使得算法不易陷入局部最优。同时，个体迁移和精英岛屿的变异策略以及参数自适应，加强了收敛结果的精度，因此收敛成功率高。在测试函数f4上，DADE、aDE、和EIDE均有较高的收敛成功率，但DADE和aDE的迭代均值均未能成功收敛，因为这两个算法多次运行时均存在优化结果适应度值很大的情况，影响了适应度均值。在测试函数f7上所有算法收敛成功率均小于等于30%，并非算法不收敛，而是因为本文收敛判定阈值需要对算法收敛能力做出区分，然而结合表3可以看出算法在f7上收敛精度的差异小于一个数量级，故设置的收敛判定阈值使得算法均不完全成功收敛，通过比较算法收敛成功的比例对比算法收敛能力，可见EIDE算法在测试函数f7上较其他算法收敛能力明显更强。而对于测试函数f7、f8可以看出，各算法虽然都能到达收敛阈值，但EIDE算法所需的平均最小收敛代数较其他算法均少90代以上，说明其收敛速率较其他算法明显更高。

图3绘制了6种算法在4个标准测试函数下的收敛曲线，其中折线图标题为该图数据对应的测试函数，结合表4所示，可知EIDE算法收敛速度快。在所有算法均成功收敛的4个测试函数上，EIDE成功收敛所用的迭代次数都是最少的。且如收敛图所示，在多个测试函数上收敛速度较其他算法明显更快。因为精英岛屿的变异策略以及参数自适应方法加速了算法收敛，同时优质个体在精英岛屿上的集中，以及通过个体迁移方式增加最佳岛屿个体数量的方法，加强了当前最优解周围的搜索，加速了收敛。

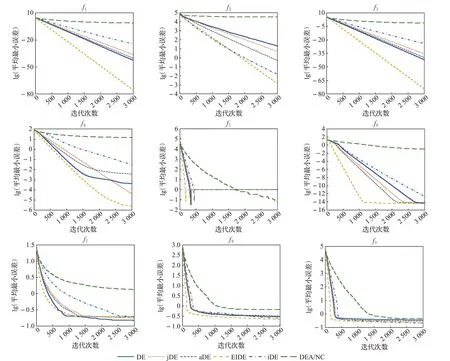
图3 各算法收敛过程曲线比较图Fig.3 Comparison of convergence process curves of each algorithm

4 结束语

为了避免差分进化算法常见的早熟收敛和搜索停滞问题，同时提高精度并加速收敛，本文将精英化思想引入岛屿模型的差分进化算法中，设计了岛屿分类和“个体迁移”策略集中精英个体；通过使用方向增强的变异策略，并设计了自适应的控制参数方法，增加算法搜索精度与收敛速度；利用岛屿间有向的“移民”策略，保持种群基因多样性，防止早熟收敛和搜索停滞问题。本文进而提出了一种基于精英化岛屿种群的差分进化算法（EIDE）。本文将该算法与5种经典的改进差分进化算法在9个标准测试函数上进行优化精度和收敛速度的比较实验。实验结果表明：EIDE算法相较于其他几种对比算法在准确性、稳定性、收敛速率方面具有明显提升。但是，本文并没有对算法的执行时间进行详细研究，而执行时间一直是制约进化算法应用的一个重要问题，多种群的差分进化算法，具有高度的可并行性。因此，如何在分布式平台上优化EIDE算法的并行能力、加速算法执行是下一步的研究工作。