LR攻击和TCSC接入对电力系统可靠性的影响分析

2021-10-28张乐涛刘海涛赵美莲

电力系统及其自动化学报 2021年10期

陈凡，张乐涛，张强，刘海涛，史杰，赵美莲

（1.南京工程学院电力工程学院，南京 211167；2.江苏省配电网智能技术与装备协同创新中心，南京 211167）

随着智能电网建设和信息通信技术的高速发展，电力系统与信息控制设备和通信网络深度融合，形成了电力信息物理系统，然而通信网络和信息设备的安全漏洞给电力系统的安全运行带来了新的挑战[1-2]。虚假数据注入攻击通过篡改状态估计值诱导调度员误操作，从而危害系统的安全经济运行，具有较强的可达性、隐蔽性与干扰性，是对电力系统威胁程度较高的网络攻击方式之一[1]。实际情况中发电厂控制室与系统控制中心存在直接通信，因此能方便地检测出针对发电机出力的虚假数据注入攻击。为此，文献[3]提出了负荷重分配LR（load redistribution）的网络攻击形式，攻击者仅对负荷和线路功率等有限的测量信息进行篡改，被认为是一种实际可行的虚假数据注入攻击形式。

近年来研究人员围绕LR攻击的建模及模型的求解算法开展了相关的研究：文献[3]提出了即时LR攻击，通过最大-最小攻击者-防御者模型确定了最具破坏性的LR攻击，利用Karush-Kuhn-Tucker（KKT）条件将双层模型转化为单层模型进行求解；文献[4]在文献[3]的基础上进一步考虑了电力系统内部人员泄露信息的风险；文献[5]提出了基于不完全网络信息的区域攻击模型；文献[6]提出了连续LR攻击模型，并利用相关链模型捕获系统中的脆弱支路，防御连续LR攻击；文献[7]利用LR攻击掩饰线路遭受攻击，提出了将LR攻击与线路物理攻击相结合的协同攻击模型；文献[8]研究了LR攻击和线路物理协同攻击对电-气耦合系统的影响；文献[9]提出了考虑LR攻击、线路攻击和发电机攻击的双层协同攻击模型；文献[10]针对信息-物理协同攻击，提出了一种应对协同攻击的电力系统随机规划模型，该模型通过优化新增机组和线路来防御协同攻击，最大程度的减小协同攻击造成的系统切负荷；文献[11]分析了延时攻击对经济调度的影响，建立了考虑延时LR攻击的三层负荷削减优化模型；文献[12]基于半马尔科夫过程建立了LR攻击的不确定性模型，基于KKT条件求解考虑LR攻击的负荷削减优化模型，研究LR攻击对系统可靠性的影响。

同时，随着电力电子技术和控制技术的发展，柔性交流输电FACTS（flexible alternative current transmission system）技术已成为增强电网灵活性的重要手段之一。作为常用的FACTS装置之一，TC⁃SC能够改变潮流分布、降低线路的潮流越限风险[13]。现有文献针对TCSC设备接入对系统运行分析的影响开展了研究：文献[14]研究了含TCSC电力系统可靠性的非同调问题；文献[15]研究了TCSC对电网运行风险和调度运行成本的影响；文献[16]以提高风电利用率为目标，研究了TCSC的选址问题。上述研究中，包含TCSC的系统状态分析模型均可用最优潮流模型的形式表示，然而当计入LR攻击的影响时，由于涉及攻击者和运行人员之间的交互作用，包含TCSC的系统状态分析模型将不再是单层的最优潮流模型，而是变成了双层规划模型。目前尚未见到文献对计入LR攻击和TCSC作用的系统可靠性评估问题进行研究。

综上所述，现有文献在进行电力系统可靠性评估时较少考虑LR攻击的影响，对于LR攻击作用背景下TCSC接入对系统可靠性影响的问题也缺乏研究。为此，本文对考虑LR攻击和TCSC接入的电力系统可靠性评估问题开展研究。首先，分析了LR攻击和TCSC接入对系统状态分析的影响，建立了考虑LR攻击和TCSC的系统负荷削减模型；其次，提出了基于非序贯蒙特卡洛的考虑LR攻击和TC⁃SC的电力系统可靠性评估算法；最后，在IEEE RTS79修改系统上进行算例分析，研究了LR攻击和TCSC接入对系统可靠性的影响。

1 考虑LR攻击的负荷削减模型

LR攻击过程是一个典型的博弈过程，LR攻击作用下攻击者和调度员之间交互作用的示意如图1所示，其中ΔD是对负荷节点的攻击量矩阵；S是节点负荷削减量矩阵。上层攻击者以系统负荷削减量最大为目标，在躲过不良数据检测的条件下向系统注入负荷攻击数据ΔD；下层调度方以负荷削减量最小为目标，根据接收到的系统状态估计信息（含虚假的负荷数据）进行安全校正、得到最优负荷削减的结果S，S也即是攻击方案ΔD造成的系统切负荷结果。在LR攻击情形中，上层攻击者实施攻击方案ΔD对应的攻击效果（即系统负荷削减量S）需要在下层调度员实施校正措施之后才能获取，而下层调度员则是依据接收到的被篡改过的负荷数据进行安全校正。由此可见，在LR攻击的作用下，攻击者和调度员都会采取相应的措施去最大化自己的利益，双方之间交互作用的博弈过程可以用双层优化模型来表示。

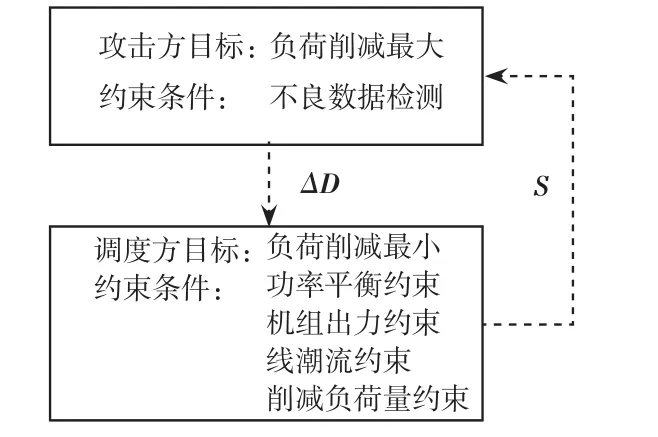
图1 考虑LR攻击的负荷削减模型Fig.1 Load-shedding model considering LR attack

1.1 上层攻击模型

上层攻击者的目标是使得负荷削减量最大，目标函数为[3]

式中：Nd为系统负荷节点的总数；Sd为负荷节点d的负荷削减量。

为了绕过不良数据的检测，攻击方发起的攻击方案需要满足以下条件：负荷注入攻击量总和为零、线路潮流攻击量与负荷攻击量满足网络拓扑结构关系、负荷攻击量应在合理的范围内。上述约束条件可以表示为[3]

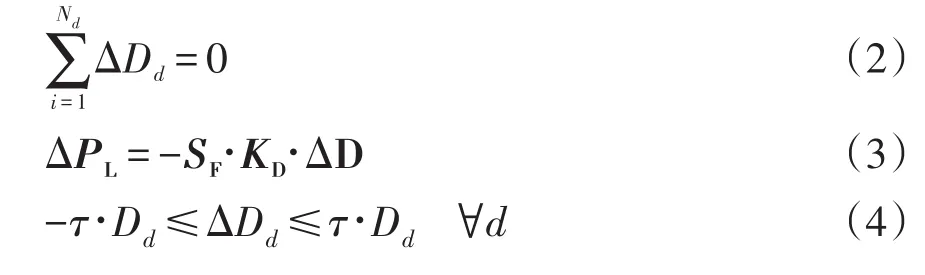
式中：ΔDd为对负荷节点d的攻击量；Dd为负荷节点d的负荷；ΔD为对负荷节点的攻击量矩阵，ΔPL是对线路潮流的攻击量矩阵；SF为转移矩阵；KD为节点-负荷关联矩阵；τ为负荷攻击系数，取值为0.5。

通过约束条件式（2）～（4），攻击方得到的攻击方案ΔD有很多种，将每一种ΔD带入下层模型可求得对应的负荷削减结果，该负荷削减结果也是上层目标函数中的负荷削减量。

1.2 下层调度模型

考虑LR攻击的负荷削减模型的下层模型与传统电力系统可靠性评估中的最优负荷削减模型类似，区别在于当计及LR攻击时，负荷削减模型中的节点负荷数据受到上层模型的影响。下层调度员在攻击方案ΔD下经过最优负荷削减调度求得的负荷削减结果S，它代表了攻击方在方案ΔD下得到的负荷削减攻击效果。下层调度模型的目标函数为[3]

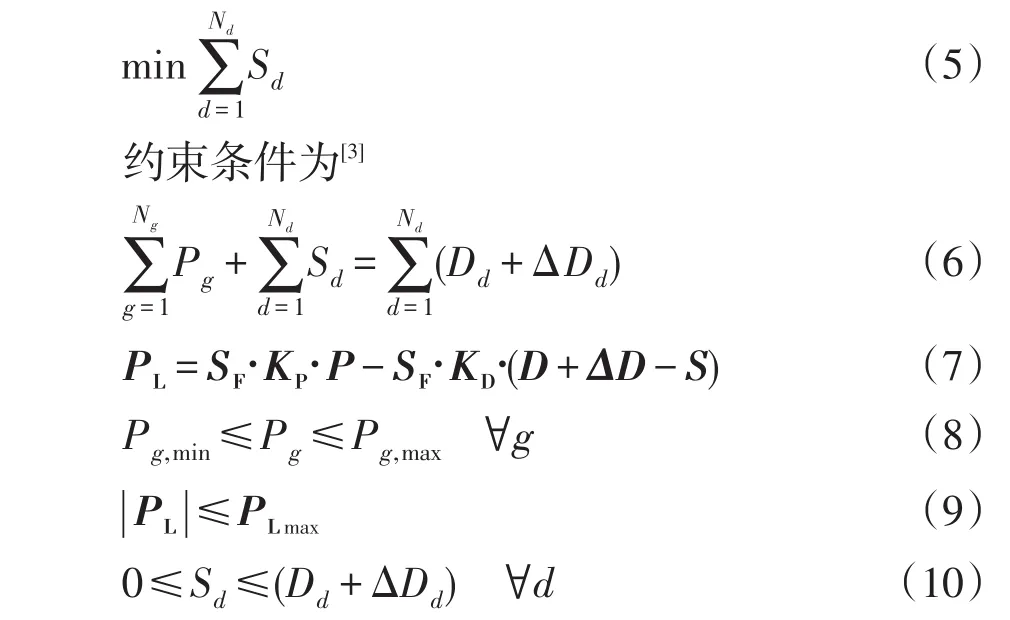
式中：Ng为发电机总数；Pg为发电机g的有功出力；PL为线路有功潮流矩阵；KP为节点-发电机关联矩阵；P为发电机有功出力矩阵；D为节点负荷矩阵；Pg,min和Pg,max分别为发电机g的最小有功出力和最大有功出力；PLmax为线路容量矩阵；式（6）为系统的有功平衡式；式（7）为线路潮流计算式；式（8）为发电机有功出力约束；式（9）为线路潮流约束；式（10）为负荷削减量约束。

2 考虑LR攻击和TCSC的负荷削减模型

2.1 含TCSC的等值线路模型

2.1.1 含TCSC的等值线路潮流模型

在实际应用中，常将TCSC和一个旁路断路器BB并联后再串接到线路中去，当TCSC发生故障后，旁路断路器BB可以将TCSC旁路，从而保证线路的继续运行。假设线路ij安装TCSC，TCSC可用可变电抗来表示，含TCSC等值线路模型如图2所示[17]。

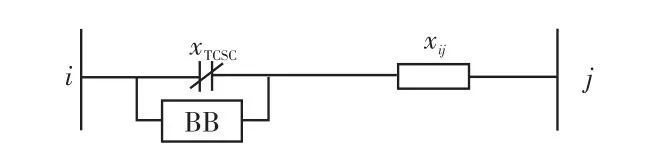
图2 含TCSC的等值线路模型Fig.2 Model of equivalent line with TCSC

式（11）～（14）中：θi和 θj分别为节点 i和 j的相角；xij为线路ij的电抗；xTCSC为TCSC的电抗；rTCSC为TCSC的电抗改变系数。

2.1.2 含TCSC的等值线路可靠性模型

含TCSC的等值线路共有3种运行状态：

（1）正常补偿运行状态，线路ij和TCSC正常工作，此状态下TCSC的补偿作用有利于改善系统可靠性；

（2）无补偿运行状态，TCSC故障后，线路ij被断路器BB旁路，线路ij恢复运行，此状态相当于线路ij没有安装TCSC的情况；

（3）退出运行状态，线路ij故障，或者线路ij正常工作，但TCSC和BB同时故障。可见，TCSC的接入会导致串补线路退出运行的状态概率增加。

线路ij、TCSC和BB的运行状态互相独立，假设每个元件只有正常工作和故障2种状态，则含TCSC等值线路处于各个运行状态的概率为[14]

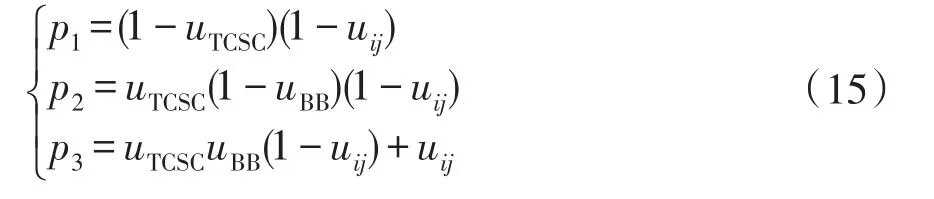
式中：p1、p2、p3别为3种运行状态的概率；uij为线路ij的不可用率；uTCSC为TCSC的不可用率；uBB为BB的不可用率。

2.2 考虑LR攻击和TCSC的系统状态分析模型

考虑LR攻击的负荷削减上层模型中，攻击者的攻击决策与线路电抗无关，因此TCSC的接入不会对上层模型产生影响，计及TCSC和LR攻击的系统状态分析模型的上层模型仍可由式（1）～式（4）表示。然而，TCSC的接入将会对考虑LR攻击的负荷削减下层模型产生影响。TCSC接入之后，调度方除了进行发电机组出力重新调度之外，还可以通过调节TCSC参数改变其所在线路的等值电抗，从而提高系统潮流分布的调节能力，这使得TCSC有可能缓解LR攻击，减少LR攻击造成的负荷削减量。当计入TCSC的作用时，应在考虑LR攻击的下层模型中增加与线路电抗相关的TCSC控制变量的约束，即

式中，rTCSC,max和rTCSC,min分别为TCSC控制变量的上、下限。

考虑LR攻击和TCSC的系统状态负荷削减模型由式（1）～（10）和式（16）来表示，该模型是一个混合整数非线性双层优化模型，本文采用文献[11]提出的含重启框架的Benders分解法对该模型进行求解。

3 考虑LR攻击和TCSC接入的电力系统可靠性评估算法

电力系统可靠性评估主要包含系统状态抽取、系统状态分析和可靠性指标计算等3个步骤，同传统的电力系统可靠性评估相比，计及LR攻击的电力系统可靠性评估在上述3个步骤中的不同体现在：

（1）系统状态抽取。传统的系统可靠性只需要抽取发电机组和输电线路的状态，计及LR攻击后还需要抽取LR攻击状态，判断是否发生LR攻击。

（2）系统状态分析。传统的系统可靠性评估只涉及单层的最优负荷削减模型，而计及LR攻击的系统可靠性评估除了涉及单层的最优负荷削减模型之外，还涉及双层的负荷削减优化模型，该双层优化模型表征了LR攻击下攻击者和调度员之间的博弈过程。

（3）可靠性指标计算。传统的系统可靠性评估中，最优负荷削减的结果即是所抽取的系统状态下的负荷削减量；计及LR攻击的系统可靠性评估中，每个系统状态对应的负荷削减量除了包含单层的最优负荷削减结果之外，还包括LR攻击造成的负荷削减量。

本文提出的基于非序贯蒙特卡洛的考虑LR攻击和TCSC接入的系统可靠性评估算法流程图如图3所示，具体的步骤如下：

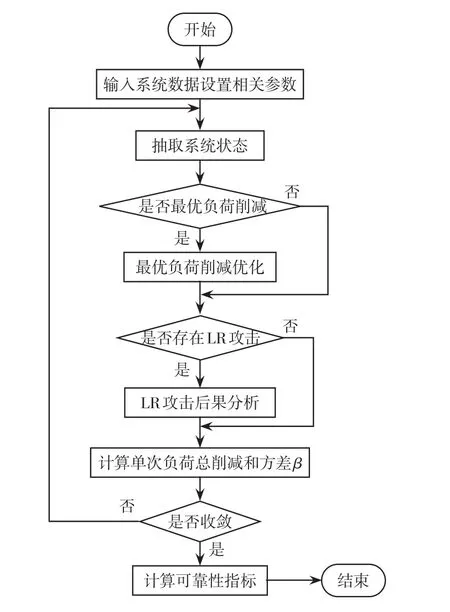
图3 考虑LR攻击和TCSC接入的可靠性评估算法流程Fig.3 Flow chart of reliability evaluation algorithm considering LR attack and TCSC access

（1）输入系统数据和设置相关参数，主要包括发电机参数、线路参数、LR攻击成功概率、TCSC和旁路断路器的不可用率以及收敛条件等。

（2）抽取系统状态。主要包括发电机、输电线路及含TCSC的等值线路的运行状态。

（3）判断是否需要进行最优负荷削减。对系统状态进行分析，判断机组出力是否满足负荷要求、线路潮流是否越限，从而决定是否需要进行最优负荷削减优化。若该状态需要进行最优负荷削减优化，转到（4）；否则，转到（5）。

（4）最优负荷削减优化。对抽取的系统状态进行最优负荷削减优化，得到系统最优负荷削减量。

（5）判断是否发生LR攻击。生成随机数，将该随机数与LR攻击成功概率比较。若该随机数小于LR攻击成功概率，说明发生LR攻击，转到（6）；否则，转到（7）。

（6）LR攻击后果分析。首先，判断当前系统状态是否进行过最优负荷削减，若该状态进行过最优负荷削减优化则节点负荷的可攻击量应减去最优负荷削减值；其次，采用含重启框架的Benders分解方法求解计及LR攻击和TCSC的双层负荷削减优化模型，计算LR攻击造成的负荷削减量。

（7）计算当前系统状态的负荷削减量和更新指标方差系数。将最优负荷削减的结果和LR攻击切负荷的结果相加即得到当前系统状态的总负荷削减量，再进一步更新指标方差系数。

（8）判断是否满足收敛条件。若方差系数小于收敛系数或者抽样次数达到设定的最大抽样次数，转到（9）；否则，转到（2）。

（9）计算系统可靠性指标。

为了更好的量化LR攻击对系统可靠性造成的影响，定义了LR攻击平均切负荷量指标（AVG_LR），它表征了LR攻击造成系统切负荷的严重程度，表达式为

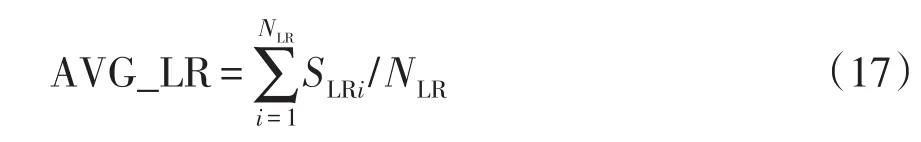
式中：NLR为LR攻击成功次数；SLRi为第i次LR攻击造成的切负荷量；AVG_LR的单位为MW·次-1。

4 算例分析

以修改后的IEEE RTS79可靠性测试系统为例，分析了LR攻击以及TCSC接入对电力系统可靠性的影响。IEEE RTS79系统参数见文献[18]，为了突出LR攻击的作用，在本文研究中将IEEE RTS79系统的线路容量修改为原容量的60%。采用非序贯蒙特卡洛模拟系统运行状态，收敛条件为系统电量不足期望EENS（expected energy not supplied）的方差系数小于5%。为了克服蒙特卡洛算法波动性的影响，本文通过随机抽样生成100 000组随机数作为系统状态源种子，算例分析中的系统状态样本均源自于这些种子。

4.1 LR攻击对系统可靠性的影响分析

LR攻击的成功概率与攻击方的攻击水平和系统防御措施相关，文献[12]建立了考虑攻击水平和系统防御措施的LR攻击概率模型。本文采用文献[12]给出的LR攻击概率模型分析不同LR攻击成功概率下的系统可靠性，3种LR攻击成功概率Pattack分别是：0.004（攻击方新手水平、系统加密）、0.011（攻击方专业水平、系统加密）和0.026（攻击方专业水平、系统不加密）。基于系统状态源种子和方差系数收敛条件，计算不同LR攻击成功概率下的系统可靠性指标，计算结果如表1所示。

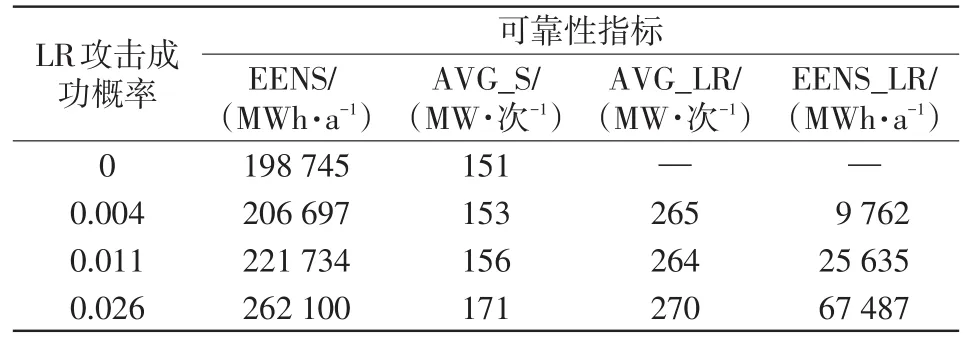
表1 不同LR攻击成功概率下的系统可靠性指标Tab.1 System reliability indices under different values ofPattack

表1中，EENS是系统电量不足期望；AVG_S是系统的平均切负荷量，是指系统总的切负荷量除以系统总的切负荷次数；EENS_LR是LR攻击造成的系统电量不足期望。由表1可见：随着LR攻击成功概率的增加，系统EENS也随之增加。这是因为LR攻击通过注入虚假数据欺骗调度员做出新的调度方案，从而造成系统的切负荷，增加了系统的切负荷量，因而系统EENS增加。

4.2 TCSC接入对系统可靠性的影响

将TCSC控制变量rTCSC的范围设定为[-0.5，0.5]，并根据文献[14]设定TCSC和旁路断路器BB的可靠性参数：TCSC的不可用率取0.011 844 33，旁路断路器BB的不可用率取0.000 365 16。在线路10-12安装TCSC，其不可用率为0.001 750 36[18]，计算得到含TCSC的等值线路三状态模型如表2所示。由表2可见，TCSC接入线路之后，一方面所接入的线路在绝大多数情况下都处于正常补偿运行状态，有利于提高系统可靠性；另一方面，线路处于退出运行状态的概率略有增加，不利于系统可靠性的改善。因此在实际应用中为了保证TCSC接入对系统可靠性的改善作用，应尽可能选择高可靠性的TCSC设备及旁路断路器设备。

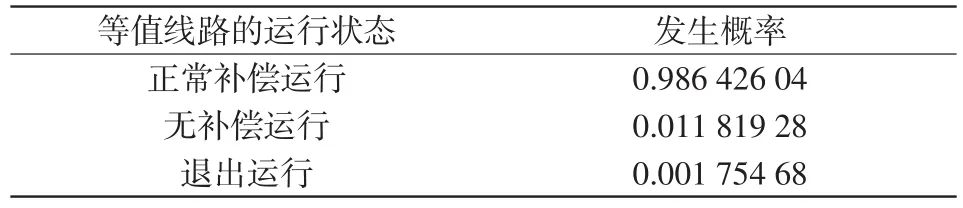
表2 含TCSC的等值线路三状态模型Tab.2 Three-state model of equivalent line with TCSC

为了研究TCSC接入对系统可靠性的改善作用，首先基于固定的随机数种子和方差系数收敛条件抽取发电机和线路的运行状态，然后再针对所抽取的发电机和线路组成的系统状态，分别计算TC⁃SC接入前后的系统可靠性指标，如表3所示。由表3可见：TCSC接入总体上可以减小系统EENS，改善系统可靠性。其中，TCSC对输电系统故障的改善作用最大，对发电系统故障基本起不到改善作用。输电系统故障引起的切负荷是由于线路故障造成潮流越限引起，TCSC可以改变线路电抗，调节系统潮流分布，有效缓解输电阻塞问题。发电系统故障引起的切负荷是由于机组故障造成出力不足引起，TCSC对发电系统故障的改善作用很小。

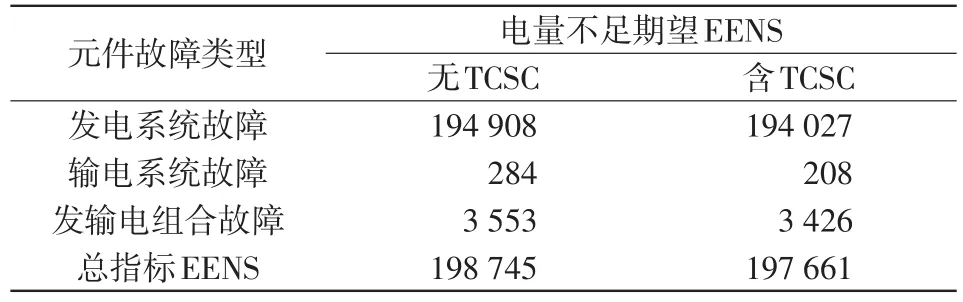
表3 TCSC接入前后的系统可靠性指标Tab.3 System reliability indices with and without TCSC MWh·a-1

论文进一步研究了TCSC和旁路断路器BB可靠性参数对TCSC改善系统可靠性作用的影响。针对相同的系统状态样本，通过按比例同时增加TC⁃SC和BB的不可用率，得到系统EENS随TCSC和BB不可用率变化的曲线如图4所示。由图4可以看出：随着TCSC和BB不可用率的增加，系统的EENS也逐渐增加，TCSC对系统可靠性的改善作用逐渐减小；当不可用率提升至原来的45倍时，TCSC接入后的系统EENS反而高于不含TCSC时的系统EENS。通常情况下，旁路断路器BB的可靠性很高，能在TCSC退出运行时迅速将其旁路，保证了线路的继续运行，因此图4中才会在TCSC和BB的不可用率倍数提高到45倍时才发生装设TCSC之后的系统可靠性反而变差的问题，这也再次表明：实际应用中为了获得较好的可靠性改善效果，应尽可能选择可靠性较高的TCSC和旁路断路器设备。

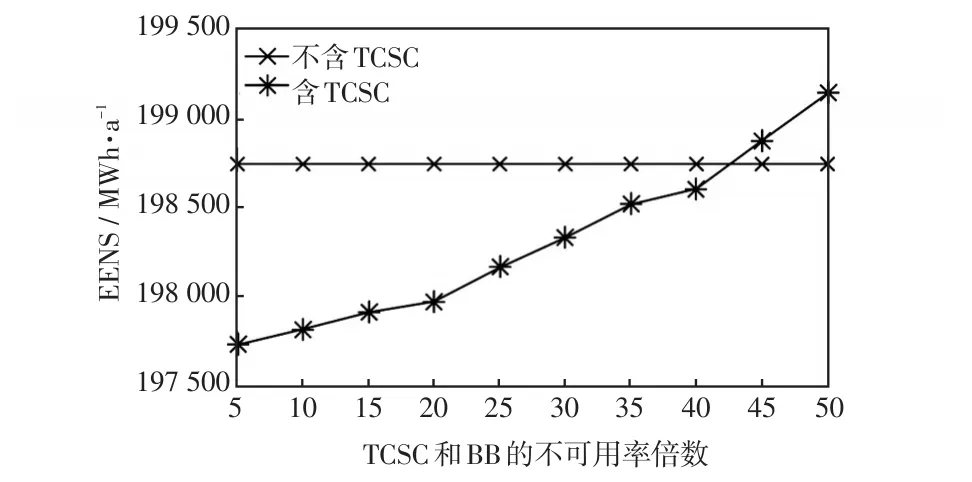
图4 TCSC和BB的不可用率对系统EENS的影响Fig.4 Impacts of unavailability of TCSC and BB on system EENS

4.3 考虑LR攻击和TCSC接入的系统可靠性

为了研究LR攻击情形下，TCSC接入对系统可靠性的改善作用，首先在LR攻击成功概率为0.011的情况下，基于固定的随机数种子和方差系数收敛条件抽取包含发电机和线路的运行状态、LR攻击事件等信息的系统状态样本，接着再基于所抽取的系统状态样本比较TCSC接入前后的系统可靠性指标。LR攻击成功概率为0.011时TCSC接入前后的系统可靠性指标如表4所示，EENS_opf是最优负荷削减的电量不足期望。

由表4可以看出：接入TCSC之后，系统的EENS、EENS_opf、EENS_LR、AVG_LR等指标均有一定程度的减少，TCSC的接入能一定程度上缓解LR攻击对系统可靠性的影响。特别说明的是，表3和表4中由于发电机、输电线路等物理元件故障造成的系统最优负荷削减量之间存在差异，这是由于在以EENS方差系数作为收敛条件的情况下表3和表4的系统状态样本并不相同而造成的。

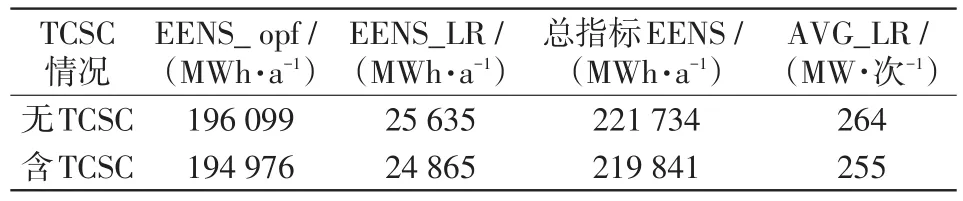
表4 考虑TCSC和LR攻击的系统可靠性指标Tab.4 System reliability indices considering TCSC and LR attack

本文进一步研究了不同线路容量和负荷水平情况下TCSC接入在缓解LR攻击对系统可靠性影响方面的作用。将IEEE RTS79系统线路容量分别设为原容量的60%、70%和80%时的AVG_LR指标如图5所示；线路容量设为IEEE RTS79系统原始容量的60%，负荷水平分别设为原来的0.9倍、0.95倍和原负荷水平时的AVG_LR指标如图6所示。

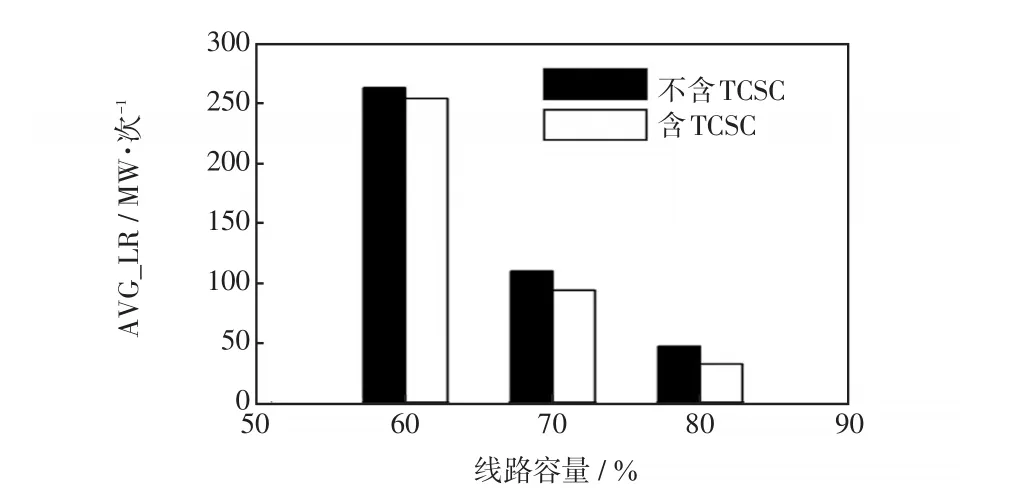
图5 不同线路容量下的AVG_LR指标Fig.5 Index of AVG_LR under different line capacities

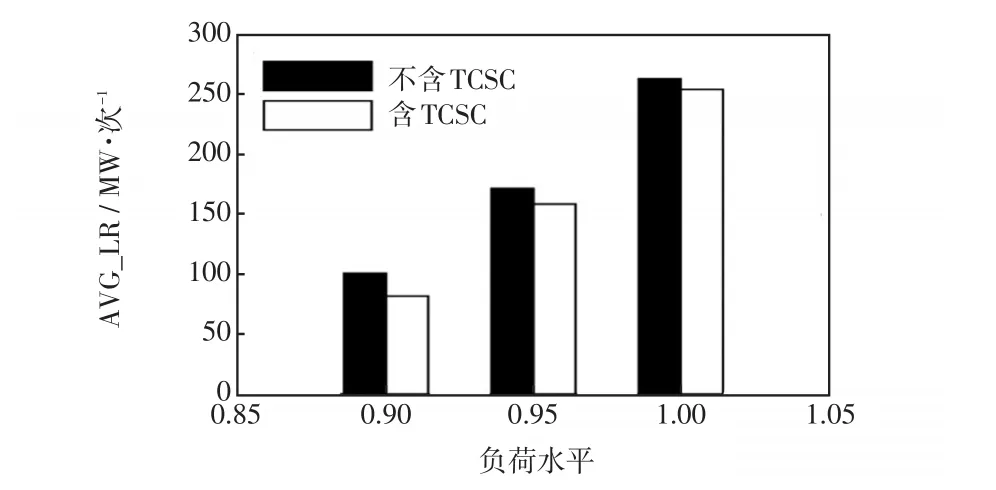
图6 不同负荷水平下的AVG_LR指标Fig.6 Index of AVG_LR at different load levels

由图5可见，随着线路容量的减少，LR攻击造成的切负荷量逐渐增加，TCSC对LR攻击的改善作用逐渐减少。这是因为LR攻击通过注入虚假数据欺骗调度员做出新的调度方案，该调度方案在线路容量不足的情况下容易造成切负荷。当线路容量降低时，TCSC虽然可以调节系统潮流分布，但却无法改善系统整体传输容量不足的情况，故TCSC的缓解作用大大降低。

由图6可见，随着负荷水平的增加，LR攻击造成的系统切负荷量逐渐增加、TCSC对LR攻击的改善作用逐渐减小，原因在于两个方面：其一，与线路容量减少时类似，负荷水平的增加使得输电充裕度不足、限制了TCSC的潮流调节能力；其二，从攻击者的角度来看，负荷的增长增加了LR攻击的可攻击量。