基于多故障冲击模型和故障树的PFDavg计算方法研究*
2021-05-12赵智聪靳江红王妤甜
赵智聪,靳江红,王 庆,王妤甜
(1.首都经济贸易大学 管理工程学院,北京 100071; 2.北京市劳动保护科学研究所,北京 100054)
0 引言
安全仪表功能(Safety Instrumented Function,SIF)在保障化工等过程工业的安全性方面起着重要的作用。为有效保证SIF的可靠性和安全性,需要计算SIF的要求时危险失效平均概率(Average Probability of Dangerous Failures on Demand,PFDavg),评估该系统的安全完整性等级(Safety Itegrity Level,SIL)。
目前,我国已经发布了《电气/电子/可编程电子安全相关系统的功能安全》(GB/T 20438—2017)[1],学者们针对功能安全的研究越发深入。国内外学者针对安全仪表功能PFDavg计算进行大量研究。张斌等[2]、李宏浩等[3]、李荣强等[4]、马志国等[5]提出利用蒙特卡洛(Monte Carlo)、马尔科夫(Markov)以及简化方程式等模型计算PFDavg的新方法;李军丽等[6]、夏阳光等[7]、岑康等[8]利用动态故障树和FFTA-LOPA等模型对SIL验证方法进行研究;王锴等[9]、Chebila[10]、Mechri等[11]则对SIF共因失效分析进行深入探索。阳宪惠等[12]以及Goble[13]提出利用β失效模型和故障树模型计算安全仪表系统PFDavg的方法,虽建立了考虑共因失效的PFDavg计算模型,但由于β模型不能区分多重共因失效对SIF的影响,在对可能产生多重共因失效的SIF进行PFDavg计算时误差较大,有可能高估SIF的安全性。综上所述,本文引入多故障冲击模型(Multiple Error Shock Model,MESH)[14]分析多重共因失效对SIF的影响,并将其与故障树方法相结合,建立可准确计算SIF的PFDavg数学模型,并以某石化公司的安全仪表功能为例进行验证。
1 故障树方法计算PFDavg的原理
1.1 基本参数设定
设定失效率λ为常量,失效率概率密度函数服从指数分布。本文仅针对可修复系统的PFDavg计算进行讨论。
1.2 PFDavg的故障树计算模型
考虑共因失效的简单故障树如图1所示。
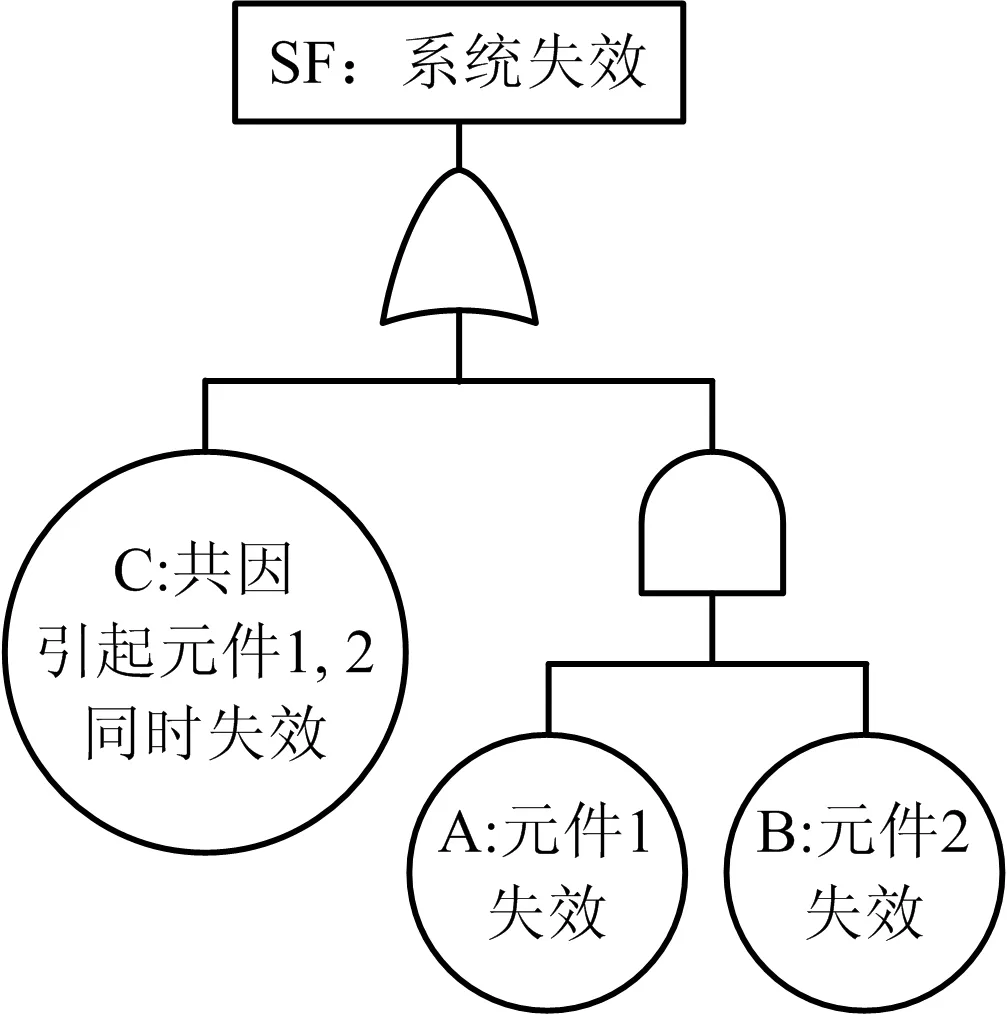
图1 考虑共因失效的故障树Fig.1 Fault tree considering common cause failure
假设无论其他元件在[0,t]上处于何种状态,各单独元件在时刻t的失效概率均是与之相互独立的,通过故障树逻辑关系可知,系统失效概率计算如式(1)所示:
PSF(t)=PC(t)+PA(t)PB(t)-PC(t)PA(t)PB(t)
(1)
式中:Pi(t)为元件i在t时刻的瞬时失效率,i即SF,A,B,C。
系统的瞬时不可用率计算如式(2)所示:
USF(t)=UC(t)+UA(t)UB(t)-UA(t)UB(t)UC(t)
(2)
式中:Ui(t)为元件i在t时刻的瞬时不可用率,i即SF,A,B,C。
《电气/电子/可编程电子安全相关系统的功能安全第6部分:GB/T 20438.2和GB/T 20438.3的应用指南》(GB/T 20438.6—2017)[15]中定义PFDavg为系统的平均不可用率。根据PFDavg定义,PFDavg(T)计算如式(3)所示:
(3)
式中:PFDavg(T)为SIF在[0~T]时间内的要求时危险失效平均概率;MDT(t)为SIF在[0~T]时间内的平均不工作时间。
1.3 系统瞬时不可用率的计算
瞬时不可用率U(t)定义为:“1个元件在时刻t不能够正常工作的概率。”所以,以元件在时刻t的失效概率为指标衡量系统的瞬时不可用性。由于失效概率服从指数分布,则元件在t时刻的失效概率计算如式(4)所示:
P(t)=1-e-λt
(4)
式中:λ为元件失效率;P(t)为元件在t时刻的失效概率;
由于λ通常小于10-41/h,当λ较小时,根据泰勒展开式可以得到元件失效概率近似计算公式,如式(5)所示:
P(t)=λt
(5)
则PλDD(t),PλDU(t)计算公式如式(6)~(7)所示:
PλDD(t)=λDD×MTTR
(6)
PλDU(t)=λDU×TI
(7)
式中:PλDD(t)为可检测到的危险失效概率;PλDU(t)为未检测到的危险失效概率;λDD为可检测到的危险失效率;λDU为未检测到的危险失效率;MTTR为平均修复时间;TI为检验测试周期。
整个系统危险失效的失效概率计算公式如式(8)所示:
PλD(t)=PλDD(t)+PλDU(t)=λDD×MTTR+λDU×TI
(8)
2 基于多故障冲击模型的PFDavg计算
2.1 多故障冲击模型(MESH)
多故障冲击模型的目标是计算出每次冲击造成1个,2个或者多个元件失效的失效率。定义每次冲击导致n个元件失效的失效率计算公式如式(9)~(11)所示:
(9)
(10)
M=P(1)+P(2)×2+P(3)×3+…P(n)×n
(11)
式中:λ(n)为每次冲击导致n个元件失效的失效率;υ为冲击率;n为元件数;M为每次冲击下故障元件的平均数;P(n)为每次冲击导致n个元件发生故障的概率,n=1,2,3,…,n;P(1)+P(2)+…P(n)=1。
2.2 基于MESH的故障树模型
以图1中的系统为例。该系统包含2个元件,故n=2。设P(1)=a,P(2)=1-a。M的表达式如式(12)所示:
M=P(1)+P(2)×2=2-a
(12)
式中:a为每次冲击导致1个元件发生故障的概率,a≤1。
由式(9)得到计算公式如式(13)~(16)所示:
(13)
(14)
(15)
(16)
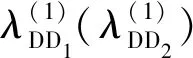
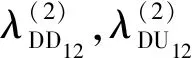
(17)
(18)
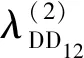
计算得到该系统的瞬时不可用率计算公式如式(19)所示:
(19)
(20)
3 实例验证
以某石化企业EO储罐液位高联锁回路的执行机构为例进行验证。该安全仪表功能执行机构整体表决模式为2oo2,其中执行机构组1表决模式为2oo2,执行机构组2表决模式为1oo1。
3.1 构建故障树
根据该SIF执行机构的系统架构创建故障树模型,如图2所示。

图2 执行机构失效故障树Fig.2 Fault tree of final element failure
3.2 PFDavg计算
由图2可知,阀门组A的瞬时不可用率计算公式如式(21)所示:
(21)
式中:UM4为阀门组A的瞬时不可用率;UX1为接口A的瞬时不可用率;UX2为电磁阀A的瞬时不可用率;UX3为球阀A的瞬时不可用率。
该企业MTTR为24 h,TI为5 a,该执行机构各元件失效率数据见表1。

表1 执行机构组A失效数据Table 1 Failure data of final element group A
将X1,X2,X3的失效率数据代入式(5),通过计算可以发现,UX1UX2,UX1UX3,UX2UX3和UX1UX2UX3的值远小于UX1,UX2,UX3。则阀门组A的瞬时不可用率计算公式如式(22)所示:
UM4=UX1+UX2+UX3
(22)
同理,可得出整个执行机构瞬时不可用率表达式如式(23)所示:
(23)

UM1计算公式如式(24)所示:
(24)
PFDavg表达式如式(25)所示:
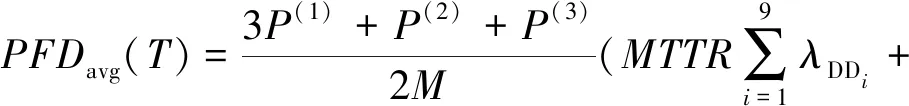
(25)
通过专家取值P(1)=0.95,P(2)=0.04,P(3)=0.01。
根据式(11)计算出M=1.06,将M,P(1),P(2),P(3),MTTR,TI以及表1中失效率数据代入式(25)得到该执行机构的PFDavg=3.58×10-2。采取相同的数据,通过商业软件exSILentia对该系统进行计算,得到其PFDavg=1.32×10-2。由计算结果可知,由于本方法中的共因失效模型能有效考虑多重共因失效的影响,所以计算出的PFDavg大于采取传统共因失效模型β模型的商业软件计算出的数值,但二者都处于相同的量级,证明此方法的先进性和可行性。
4 结论
1)结合故障树方法和多故障冲击模型,基于PFDavg的定义,建立能准确计算存在多重共因失效SIF的PFDavg数学模型。
2)结合故障树方法和MESH的PFDavg计算模型能简洁表明SIF各失效间的逻辑关系,并且,相比于马尔可夫、可靠性框图等传统方法,能更准确判断SIF的安全性。
3)在分析多重共因失效对PFDavg的影响时,每次冲击导致元件失效的概率P对计算结果影响较大,如何能获取更精确的P值还有待进一步研究。
